Sok olyan alkalom van, amely lehetőséget ad arra, hogy tanítványainkkal játsszunk olyan játékokat, amelyek a matematikai gondolkodást fejlesztik. Ilyen alkalmak például egy-egy új téma bevezetése, de lehet alkalom egy 50. vagy 100. tanóra is, vagy egy szünet előtti utolsó óra, amelyen valamiféle játékos levezetést szeretnénk nyújtani a gyerekeknek.
Erre a célra olyan játékok alkalmasak, amelyeket egyszerre sok ember tud játszani, viszonylag egyszerűek a szabályok, és lehetőleg egy-egy játék nem tart túl sokáig. Fontos szempont szokott lenni, hogy kevésbé legyen eszközigényes, vagy a kellékek egyszerűen és olcsón legyenek elkészíthetők. Sajnos ezeknek a szempontoknak nem felelnek meg az úgynevezett új generációs stratégiai táblás játékok, mert ezek általában sok pénzbe kerülnek, és egy-egy játékmenet időtartama messze túlmutat egy tanóra időkeretén.
További fontos szempont lehet, hogy az osztályban egyfajta egészséges versenyszellem alakuljon ki, azaz ne páros vagy néhány személyes játékok legyenek, hanem az egész csoport vagy osztály tudjon együtt játszani. A játékidő rövidsége lehetőséget ad arra, hogy egy-egy játék alkalmával több fordulót is lebonyolítsunk, így az osztály nagyobb része sikereket tud elérni.
Néhány olyan játékot szeretnék bemutatni, amely a fenti feltételeknek megfelel, és amelyet gyakran játszunk tanítványaimmal.
Egy megjegyzés a játékok leírása előtt. Minden játék olyan, hogy van benne egy vagy több győztes, a győzelem elég jól definiált feltételek mellett következik be. A gyerekekben azonban ott van az igény, hogy ha már nem nyertek, akkor legalább második-harmadik helyet érjenek el. Így a játékot nem kell abbahagyni, amikor kiderül, ki a győztes, lehet tovább folytatni, és kiosztani a második, illetve harmadik helyezést.
„Átkelés a folyón”
A diákoknak készíteniük kell egy játékmezőt a füzetükbe. Ezen a játékmezőn van egy folyó, amelynek egyik oldalán 1-12-ig számozott mezők vannak. A diákok kapnak fejenként 10-15 figurát – babszemet, gombot, tetszőleges választás szerint. Az egy-egy gyerek által használt figurák száma csak a játék időtartamát befolyásolja, ha hosszabb időtartamra tervezzük a játékot, akár 20-20 figurát is használhatnak. A diákok a számozott mezők között úgy osztják el a figuráikat, ahogyan akarják, tetszés szerint akár az összeset tehetik ugyanarra a mezőre, de minden figurát el kell helyezni valamelyik mezőn.
Ezután a játékvezető két hatoldalú kockával dob, és a két dobott érték összegének megfelelő mezőn levők közül minden diáknak egy figurája átkel a folyó túloldalára. A játékot az nyeri, akinek elsőként átkelt az összes figurája a folyón.
Megjegyzések: Amikor a játékot először játsszák, akkor felmerülhet a kérdés, hogy miért van szükség az 1-es számú mezőre. A gyakorlat azt igazolja, hogy néhány gyerek először tesz oda is, figyelmen kívül hagyva, hogy a dobott értékek összege legalább 2. Ez jó tanulópénz a számukra. Természetesen a továbbiakban, a kérdés tisztázása után ez a mező már elhagyható.
További érdekesség, hogy tanárként tudjuk, általában leggyakrabban a 7-es összeg, majd a 6- os és 8-as szokott előfordulni egy dobássorozatban, tehát érdemesebb középre csoportosítani a figurákat. Mivel a játékban nem dobunk túl sokszor, ezért ez a taktika nem mindig válik be, de érdemes hagyni a gyerekeket, hadd próbálgassák maguk, és az előző játékok tapasztalatait építsék be a következő játékban alkalmazandó stratégiájukba.
„Átkelés a folyón” variánsai
A játékot rendszeresen játszva az ember gyorsan felismeri, hogy tulajdonképpen a folyó szerepe elhagyható, lényegében arról van szó, hogy van egy táblázatunk 1-12-ig a számokkal, és a két dobott érték összegének megfelelő mezőről leveszünk egy figurát. Ha elkészítünk egy táblázatot, amelybe 0-18-ig számozott mezőket helyezünk, akkor az alábbi játékok játszhatók a segítségével az eredeti „Átkelés a folyón” játékon kívül:
a) A játékvezető három hatoldalú kockával dob, és a három dobott szám összegének megfelelő mezőről veszünk le egy figurát.
b) A játékvezető két hatoldalú kockával dob, és a dobott számok összegének vagy különbségének (a nagyobbikból kivonva a kisebbet) megfelelő mezőről lehet levenni egy figurát, a játékos döntésének megfelelően. – Ez a változat igényli, hogy legyen egy 0-s mező is.
c) A játékvezető három hatoldalú kockával dob, és a dobott számok összegének, vagy a legnagyobb és legkisebb dobott szám különbségének megfelelő mezőről lehet levenni egy figurát, a játékos döntésének megfelelően.
d) A játékvezető három hatoldalú kockával dob, és a legnagyobb és legkisebb dobott szám összegének vagy különbségének megfelelő mezőről lehet levenni egy figurát, a játékos döntésének megfelelően.
Az egyes változatok mind gondolkodásra kényszerítik a gyerekeket, hogy melyik szám hányféleképpen jöhet ki, azaz melyik mezőre érdemes több, melyikre kevesebb figurát helyezni, és melyikre nem érdemes helyezni egyáltalán.
Egyszámjáték, többszámjáték
A játék eredetileg Mérő László nevéhez fűződik. A játék lényege, hogy minden diák ír a füzetébe egy pozitív egész számot, a játékot az nyeri, aki a legkisebb pozitív egész számot írta egyedül.
A játék technikailag úgy játszható a legegyszerűbben, hogy a játékvezető tanár egyesével sorolja a pozitív egész számokat 1-től kezdve, és minden szám elhangzásakor azok a gyerekek, akik az adott számot írták, a magasba lendítik a kezüket. Az első olyan gyerek nyer, aki egyedül lendíti fel a kezét. Fontos, hogy a csalások elkerülése végett a gyerekek a szám elhangzásakor azonnal tegyék fel a kezüket, aki késlekedik, az kiesett a játékból.
A játék gyors, azonban előfordulhat, hogy valaki mindig az egyest írja fel. Ebben az esetben vagy ő nyer, vagy valaki a csoportból „beáldozza” magát, hogy ne az illető nyerjen, viszont így ő maga sem tud nyerni, és ez keserű szájízt okozhat. Ennek megoldására továbbfejlesztettük a játékot „kétszámjáték”-ká, illetve „többszámjáték”-ká. Az „n-számjáték”-ban minden gyerek n db pozitív egész számot ír fel a füzetébe, és az nyer, aki a lehető legkisebb számot írta fel egyedül. A játék menete hasonló az előzőhöz, mindenki akkor teszi fel a kezét, amikor olyan szám hangzik el, amit ő felírt, és az nyer, akinek legelőször van fenn a keze egyedül. Ezek a játékvariánsok kiküszöbölik a folyton egyest írók problémáját, mert így az 1 felírásával senki sem veszti el a nyerés lehetőségét.
A tantermi játék során először az egyszámjátékkal szoktuk kezdeni, és néhány kör után áttérünk a két szám, majd ismét néhány kör után a három szám stb. felírására, általában 5-ig szoktunk felmenni. A gyerekeknek mindig alkalmazkodniuk kell a többiekhez, és ahogy egyre több számot írnak fel, rájönnek, hogy esetleg csak egyre nagyobb számokkal lehet nyerni, bár előfordult, hogy ötszámjátékban a 2-essel nyert valaki.
5-ös és 5·5-ös bingó
A játékhoz szükség van egy húszoldalú dobókockára („dobóikozadérre”). Az 5-ös bingóban a gyerekek rajzolnak egymás mellé öt cellát a füzetükbe, ezekbe kell majd a dobott számokat beírni egyesével. A beírás szabálya az, hogy a beírt számok balról jobbra haladva monoton növekedő sorozatot alkossanak a végén. (Azaz egy már korábban beírt számtól jobbra legalább akkora számoknak kell szerepelni, mint ő maga.) Értelemszerűen, ha egy olyan számot dobott a kocka, amelyet valaki már nem tud beírni, akkor nem csinál semmit. A játékot az nyeri, aki először ki tudja tölteni mind az 5 mezőt a szabályoknak megfelelően.
A gyerekek gyorsan felismerik, hogy a kis számokat balra, a nagy számokat jobbra kell írni a cellákban, a döntés mindig az, hogy hány helyet hagynak a többi számnak a jobb, illetve a bal oldalon.
Ez a játék gyorsan zajlik, és általában egyszerre több győztes is van. Néhány játék után érdemes áttérni az 5·5-ös változatra. 
Ebben a játékban a gyerekek a dobott számokat egy 5·5-ös táblázatba írják be úgy, hogy a beírt számok soronként balról jobbra, és oszloponként fentről lefelé haladva monoton növekedő sorozatot alkossanak. (Tehát egy már beírt szám sorában tőle jobbra, illetve az oszlopában alatta legalább akkora számoknak kell szerepelni, mint ő maga.) A játék elején lehet tisztázni a gyerekekkel, de nem feltétlenül szükséges, hogy a kisebb számok általában a bal felső sarok környékén, a közepesen nagy számok a bal alsó sarokból a jobb felsőbe menő átló környékén, a nagy számok pedig a jobb alsó sarok környékén fognak helyet kapni. (Ez persze nem törvényszerű, de sok játékban ezt az elrendezést alakítják ki a gyerekek a lehetőségeket figyelembe véve.)
A játék két változatban érhet véget:
a) Ha a dobott számot valaki nem tudja beírni a táblázatába a szabályoknak megfelelően, akkor nem csinál semmit. A játékot az nyeri, aki először kitölti a teljes táblázatot a szabályoknak megfelelően. (Ezt a játék végén mindig ellenőrizni kell, mert előfordulhat, hogy valaki rosszul csinálja, de nem veszi észre.) Lehet még egy különdíjas játékot is beiktatni, a gyerekek a dobások megkezdése előtt megtippelhetik, hogy hány dobás után fog véget érni a játék.
b) Ha a dobott számot valaki nem tudja beírni a táblázatába a szabályoknak megfelelően, akkor ki kell húznia egy még üres mezőt a táblázatában. A játékot az nyeri, aki a legtöbb számot tudja beírni a szabályoknak megfelelően. (Ezt a játék végén mindig ellenőrizni kell, mert előfordulhat, hogy valaki rosszul csinálja, de nem veszi észre.) Ez a játék értelemszerűen pontosan 25 dobás után véget ér.
Gyűjtőpóker
A játékhoz szükséges egy pakli francia kártya Jokerek nélkül, és ismerni kell hozzá a póker alapjait, azaz a póker nyerő kombinációit. A gyerekek rajzolnak egy 5·5-ös táblázatot, ennek celláiba fognak egyenként bekerülni a játékvezető által húzott kártyalapok.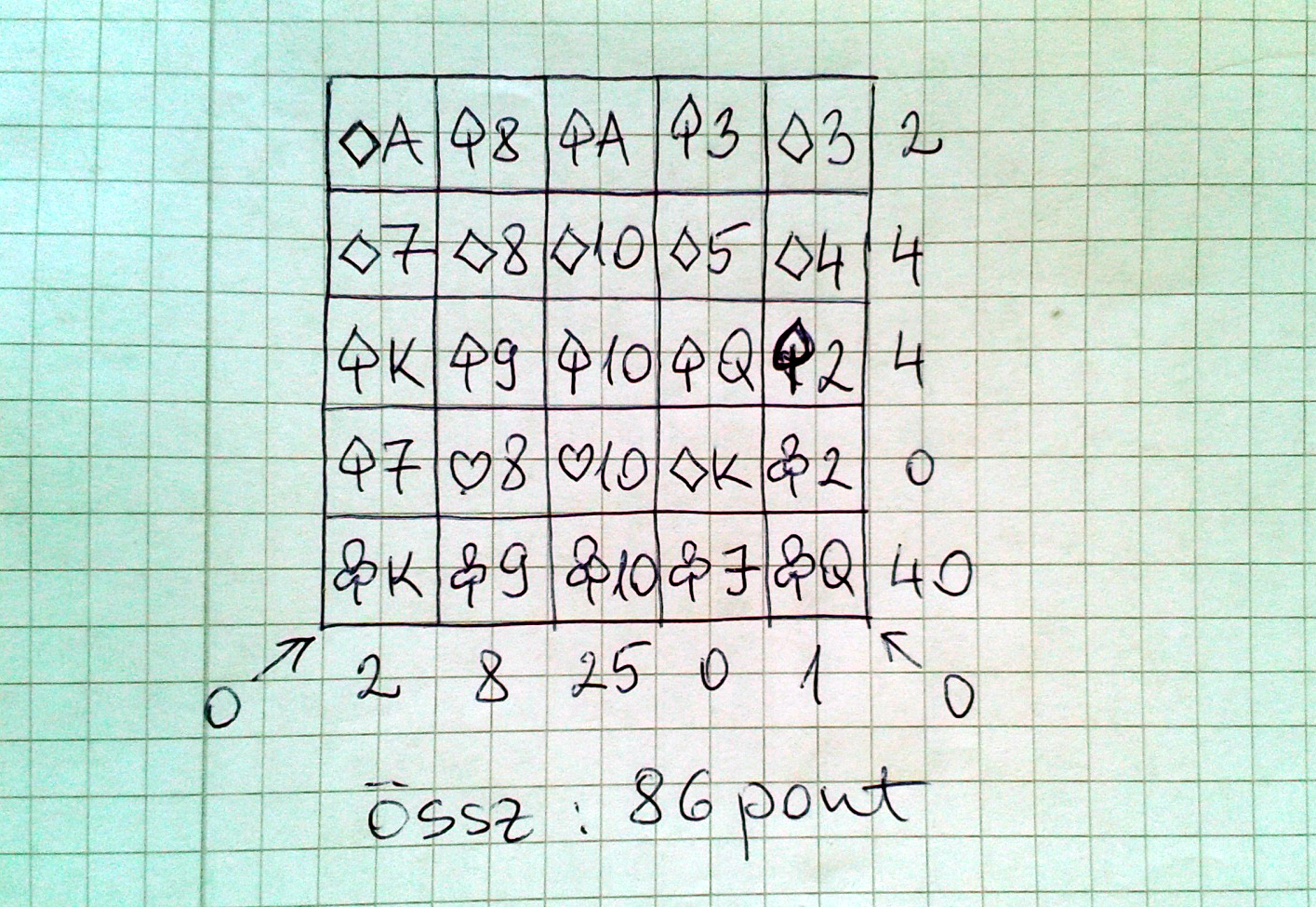 
Fontos, hogy amikor egy lap kihúzásra került, akkor azonnal el kell helyezni a táblázatban (azaz be kell írni a jelét), mielőtt a következő lap kihúzásra kerül. A játék lényege, hogy a sorok, az oszlopok, és a két nagyátló (melyek 5-5 négyzetet tartalmaznak), számítanak egy pókerlapnak, tehát mintha 12 kezünk lenne a pókerhez. A gyerekek úgy helyezik el az egyesével kihúzott lapokat a táblázatukban, hogy összességében a lehető legtöbb pontot gyűjtsék. A kitöltött táblázatot a pontozótábla alapján kell kiértékelni, minden sornak, oszlopnak és a két nagyátlónak is kialakul egy-egy pontértéke attól függően, hogy milyen nyerő kombinációt sikerült ott kialakítani, és a részpontok összege adja a teljes pontszámot. A játékot az nyeri, aki a legtöbb pontot gyűjti.
| Pókerlapok megnevezése | Magyarázat | Pontérték |
| 1 pár (1 pair) | Két egyforma értékű lap + három egymástól és ezektől is különböző értékű lap (pl. 4, 4, 5, J, K vagy 3, 5, 7, Q, Q). | 1 pont |
| 2 pár (2 pairs)) | Két egyforma értékű lap + két egyforma értékű, de az előzőektől különböző lap + egy az előzőektől különböző értékű lap (pl. 4, 4, 5, 5, K vagy 3, 7, 7, Q, Q). | 2 pont |
| Terc (drill) | Három egyforma értékű lap + két egymástól és ezektől is különböző értékű lap (pl. 4, 4, 4, J, K vagy 3, 5, A, A, A). | 3 pont |
| Szín (flush) | Mind az 5 lap azonos színű (pl. mind kőr vagy mind pikk). | 4 pont |
| Sor (straight) | Valamelyik számértéktől kezdve folyamatosan 5 egymást követő értékű lap van a kézben (pl. 3, 4, 5, 6, 7). A sor kezdődhet Ásszal (A, 2, 3, 4, 5), de körberakás nincs (K, A, 2, 3, 4 nem sor). Megjegyzés: A mi játékunk során annak nincs jelentősége, hogy az öt egymást követő értékű lap egy soron vagy egy oszlopon belül milyen sorrendben követi egymást. Tehát sor akkor is, ha fentről lefelé pl. 2, 5, 3, 4, 6 sorrendben láthatók a lapok. | 5 pont |
| Full (full house) | Két egyforma értékű lap + három egyforma értékű, de az előzőektől különböző lap (pl. 4, 4, 4, 5, 5 vagy 7, 7, 7, Q, Q). | 8 pont |
| Póker (poker) | Négy egyforma értékű lap + egy ötödik bármilyen lap. | 25 pont |
| Színsor (straight flush) | Olyan sor, amelyben minden lap ugyanolyan színű (pl. kőr 5, 6, 7, 8, 9). | 40 pont |
| Royal flush | Olyan színsor, amely a 10, J, Q, K A lapokból áll. | 800 pont |
Szuperfarmer újratöltve
A játék eredetije a Szuperfarmer játék, egy matematikai alapú stratégiai játék, amely a véletlen szabályszerűségeit felhasználva épül fel. Sajnos az eredeti játék túl hosszú és eszközigényes, nem alkalmas órai alkalmazásra. Az általam kitalált változat rövidebb (bár hosszabb, mint az eddig felsorolt játékok), és kevesebb eszközzel megoldható.
A játékhoz szükség van két tizenkét oldalú dobókockára, játékosonként egy lapra, amelyen egy folyamatos, 1-12-ig számozott, 12 mezőből álló játéktér látható, továbbá játékosonként sok figurára (babszem, számolókorong is megteszi). Minden játékos a saját játéktábláján tevékenykedik, a többiek előrehaladását nem tudja befolyásolni. Kezdetben mindenki feltesz két figurát az 1-es számú mezőre. A játékvezető a két tizenkét oldalú kockával egyszerre dob, és a játékosok feltesznek figurákat a játéktáblájukra az alábbi szabályok szerint:
Ha két különböző, 12-nél kisebb szám szerepel a két kockán, pl. a 4 és a 6, akkor először minden játékos megnézi, hogy a 4-es mezőn hány figurája van, hozzáad 1-et, elosztja az eredményt kettővel, és lefelé kerekíti. Az így kapott szám határozza meg, hogy hány új figurát tehet fel a 4-es mezőre. Ugyanezt az eljárást végrehajtja a 6-os mezővel is.
Ha két egyforma, 12-nél kisebb szám szerepel a kockákon, pl. két 7-es, akkor minden játékos megnézi, hány figurája van a 7-es mezőn, hozzáad 2-t, elosztja az eredményt kettővel, és lefelé kerekíti. Az így kapott szám határozza meg, hogy hány új figurát tehet fel a 7-es mezőre.
Ha az egyik dobott szám 12, a másik pedig nem 12, hanem pl. 3, akkor minden játékosnak az összes figuráját le kell vennie a 3-as mezőről.
Ha mindkét dobott érték 12, akkor a játékosoknak arról a mezőről le kell venniük az összes rajta levő figurát, amelyen a legtöbb figurájuk van. Ha több ilyen mező is van, akkor közülük a legmagasabb sorszámút kell kiüríteni.
A játék során minden dobás előtt a játékosok átrendezhetik figuráikat a játéktáblájukon az alábbi szabályok szerint:
1. Két figuráért, amelyek egy adott sorszámú mezőn állnak, feltehet 1 figurát az 1-gyel nagyobb sorszámú mezőre (a két „beváltott” figurát le kell vennie az érintett mezőről).
2. Egy figuráért cserébe, amely egy adott mezőn áll, feltehet két figurát az 1-gyel kisebb sorszámú mezőre (a „beváltott” figurát itt is le kell vennie az érintett mezőről).
3. Az 1. és 2. lépéseket döntése szerint akárhányszor megteheti, amíg van rá lehetősége.
4. Minden játékosnak jeleznie kell, amikor befejezte a figurák átváltását, és akkor következik a következő dobás.
Az a játékos nyer, aki először tud figurát feltenni a 12-es számú mezőre.
A játék természetesen játszható 1-6-ig számozott mezőkkel is, és két hatoldalú dobókockával, ez esetben gyorsabban véget ér, és általában kevésbé számít az alkalmazott taktika.
Nyerő nemhatos
A játékhoz egy hatoldalú kockára van szükség. A játék egy fordulója kockadobásokból áll, a játékvezető egyesével végzi a dobásokat a hatoldalú kockával. Ha 6-ost dobott, akkor a forduló véget ér, és az éppen játékban levő játékosok az adott fordulóra nem kapnak pontot. Ha nem hatost dob, akkor minden játékos eldöntheti, hogy folytatja-e a játékot, vagy kiszáll. Aki egy adott dobás után kiszáll, annyi pontot kap, ahány dobás történt eddig a fordulóban. Tehát ha a játékvezető már négyszer dobott, és egyik sem volt 6-os, akkor 4 pontot kap, aki a negyedik dobás után kiszáll. A forduló akkor ér véget, amikor mindenki kiszállt, vagy a játékvezető 6-ost dobott. A játék tetszőleges számú fordulóból állhat, érdemes ezt előre megbeszélni. A játékot az nyeri, aki a legtöbb pontot gyűjti.
Miután már sokat játszottuk ezt a játékot, rátérhetünk a profi változatára. A játékszabályok ugyanazok, néhány eltéréssel. A játék kezdetén mindenki kap 20 pontot. Ha valaki részt akar venni egy adott fordulóban, akkor ezért 2 pontot kell adnia. Ha úgy dönt, hogy nem játszik, akkor a két pontja megmarad, de nem is szerezhet pontot. A többi szabály ugyanaz.
Megjegyzés: A gyerekek egy idő után rájönnek arra, hogy a játékban hosszabb távon akkor is érdemes részt venni, ha „fizetni kell” a részvételért. Azt is könnyen láthatják, hogy a 3. dobás előtt nem fog kiszállni az, aki játszik, hiszen ha az első vagy a második dobás után kiszállna, akkor nem járna rosszabbul, ha egyáltalán nem is szállna be. Ez egyben azt is jelenti, hogy az első 3 dobást lehet egyben is ledobni, és ha van benne 6-os, akkor véget ért a forduló.
A játék lebonyolításánál praktikus, ha van sok kockája a játékvezetőnek, mert akkor egyszerű a dobások nyilvántartása: mindig másik kockával kell dobni, és a nem 6-os dobások aktuális számát a kockák egymás mellé helyezésével érdemes számon tartani.
További érdekes vizsgálat lehet, hogy kérjük meg a gyerekeket, döntsék el előre, hogy az adott fordulóban melyik dobásnál fognak kiszállni, amennyiben addig nincs 6-os, pl. a 3. dobásnál, majd ezeket a stratégiákat össze lehet hasonlítani a nyeremények alapján.
Zárszó
Remélem, hogy a fent ismertetett játékok mindenkinek jó szórakozást okoznak majd. Egyben buzdítok is arra mindenkit, hogy ha találkozik valamilyen játékkal, akkor gondolkozzon el azon, hogyan lehetne ötletet meríteni belől a fentiekhez hasonló játékokhoz, és ossza meg ezeket az ötleteket és az elkészült játékokat másokkal is.
Magyar Zsolt
Szent István Gimnázium, Budapest
