Kalmár László, a matematikus

Kalmár László (1905–1976)¹

2025. március 27-én Kalmár László Emléknapot tartottak Szegeden a jeles matematikus, az informatika hazai úttörője születésének napra pontosan 120. évfordulóján. Ebből az alkalomból a szegedi Dóm tér Nemzeti Emlékcsarnokában koszorúzást rendeztek a Matematikusok emléktáblánál, ahol Gyimóthy Tibor akadémikus, a Szegedi Tudományegyetem Természettudományi és Informatikai Kar (SZTE TTIK) Kalmár László Informatikai Intézetének professzor emeritusa mondott beszédet. A koszorúzás után a Magyar Tudományos Akadémia Szegedi Akadémiai Bizottságának (MTA SZAB) székházában az Informatikai Munkabizottság szervezésében előadások hangzottak el Kalmár László matematikai és informatikai munkásságáról, a pedagógus tanárról, Kalmár matematikai fallibilizmusáról. Fülöp Zoltán (SZTE TTIK Kalmár László Intézet) professzor emeritus megnyitója után az előadók Gyimóthy Tibor, Szabó Péter Gábor (SZTE TTIK Kalmár László Informatikai Intézet) egyetemi docens, Németh József (SZTE TTIK Bolyai Intézet) ny. c. egyetemi tanár és Máté András (ELTE BTK Logika tanszék) ny. egyetemi docens voltak. A program az MTA 200 ünnepi rendezvénysorozatának a keretébe is illeszkedett. Délután a Szent-Györgyi Albert Agórában a Neumann János Számítógéptudományi Társaság nagysikerű Kalmár 120 Emlékkiállítást szervezett az Informatika Történeti Kiállítás helyszínén, amely előreláthatólag még 2025 októberig megtekinthető lesz. A hivatalos program mellett Bohus Mihály tanár úr szervezésében további megemlékezés volt az Árpád téri Kalmár László Informatikai Intézet lépcsőházában található Kalmár-domborműnél, a Kalmár László egykori lakhelyénél (Bolyai János utca 28.) található emléktáblánál, valamint a Belvárosi temetőben, Kalmár professzor sírjánál is. Az MTA SZAB székházban elhangzott előadásokból a Kalmár László, a matematikus című előadás lejegyzett és szerkesztett változatát tesszük most közzé.

Tisztelt Hallgatóság!

A tudománytörténet-írás számára Kalmár László szegedi matematikaprofesszor életútjának és munkásságának feldolgozása és tárgyalása egy rendkívül érdekes és hálás feladat. Hálás azért, mivel a nagy mennyiségben rendelkezésre álló könyvek, cikkek, kéziratok, levelek, fényképek, visszaemlékezések, interjúk, hanganyagok és filmfelvételek, a Szegeden őrzött hatalmas Kalmár-hagyaték, kivételesen jó lehetőséget biztosít a kutatáshoz.

Az ifjú Kalmár László

Hetven évvel ezelőtt, a szintén 120 éve született egykori egyetemi évfolyamtársa és barátja, Péter Rózsa matematikus ezt írta: „Ha valaki az utolsó évtizedek magyar matematikájáról akarna tanulmányt írni, egyik főforrása Kalmár levelezése lehetne: a legkülönbözőbb területeken dolgozó matematikusok fordultak hozzá kérdéseikkel és kaptak tőle munkájukat előbbre segítő feleletet. Hozzá fordultak, mert tudták, hogy matematikus egyéniségének legfőbb vonásai: a matematika egész területének világos áttekintése, nemcsak terjedelmében, hanem mélységében is, és szinte egyedülálló pedagógiai érzék.” Péter Rózsa tapasztalatból tudta ezt, Kalmár neki egy 64 oldalas levélben írta meg az aritmetika ellentmondás-mentességére adott Gentzen-féle bizonyítás gondolatát. Negyvenöt éven át folytatott levelezésük sajtó alá rendezése még folyamatban van, a tervek szerint a Kalmárium² c. könyvsorozat következő 3. köteteként fog majd megjelenni.

Kalmár László a számítástudomány hazai atyja, a magyarországi informatika egyik úttörője, nemzetközi vonatkozásban is komputer pionír volt. A kibernetika, a számítástechnika világába a matematikai logika műszaki alkalmazási lehetőségeinek megismerése és kutatása vezette. Akkoriban egy új, születő tudományért, a számítógép-tudományért, annak elfogadtatásáért sokat kellett harcolnia, de ez a harca már tulajdonképpen akkor kezdődött, amikor még ifjú matematikusként matematikai logikával kezdett el foglalkozni.

Kalmár a matematika iránt már gimnazista korában komoly érdeklődést tanúsított, már akkor idegen nyelvű felsőbb matematikai szakkönyveket is bújt. Egyik kedves tanárának, Tóth Gézának a szakkörén már diákként arról tartott előadást, hogy szerinte, hogyan lehetne a megszokottnál természetesebb úton, kombinatorikai megfontolásokkal az e számot bevezetni. Egy másik tanára Dávid Lajos, a későbbi debreceni professzor, matematikatörténész, jeles Bolyai-kutató többször meghívta a lakására, hogy matematikáról beszélgessenek és Dávid gazdag matematikai könyvtárából könyveket nézegessenek. Kalmár sajnos mindkét szülőjét nagyon hamar elvesztette, de amíg az édesanyja élt, ő is próbált segíteni neki egy-egy külföldi matematikai szakkönyv beszerzésével.

Kalmár matematika-fizika szakos tanárként végzett a budapesti tudományegyetemen, de eljárt a Műegyetem számára érdekes kurzusaira is. Ha kérdezték, szívesen mesélt egykori egyetemi tanárairól. Két professzorának óráit különösen szerette: az egyik Fejér Lipót volt, akinek mintaszerű világos előadásaiért erősen lelkesedett. Fejérről azt mondta, hogy művésze volt a matematikának. Igaz, hogy az óráin gyakran mennyiségileg keveset tárgyalt, de azt mindig gyönyörűen tette. Egy másik kedves tanára Kürschák József volt, aki szintén nagyon világosan adott elő, és a matematikai előadásaiban pedagógusokat nevelt. Kalmár 1922-ben megnyerte az Eötvös-versenyt matematikából (ez a későbbi Kürschák-verseny), aminek folyományaként a második félévtől tagja lett az Eötvös-kollégiumnak.

1927-ben szerzett középiskolai tanári oklevelet és rögtön doktorált is, matematikából mint főtárgyból, elméleti és kísérleti fizikából mint melléktárgyakból. Témavezetője Fejér Lipót volt, disszertációját a komplex függvénytan egy interpolációelméleti témájából írta. Fejér egy egyetemi pályadíj elnyerésére jelölte korábban azt a problémát, hogy hogyan kellene valamely Jordan-görbén az interpolációs alappontokat úgy megválasztani, hogy minden ebben a zárt görbe belsejében holomorf függvény esetén az alappontokhoz tartozó Lagrange-féle interpolációs polinomok a függvényhez egyenletesen konvergáljanak.

Beke Manótól (aki Kalmárnak távoli rokona is volt) Kalmár megtudta, hogy a feladatot Carl Runge német matematikus már egy speciális esetre megoldotta. Az általános esetben Fejérnek volt eredménye, amelyből Kalmár egy elegendőségi feltételt olvasott ki. Szintén kiderült, hogy egy másik német matematikusnak, Georg Fabernek is volt egy idevágó tétele, a tétel bizonyítását azonban Kalmár nem értette meg. Nem véletlenül, mivel Fekete Mihály később felvilágosította, hogy a bizonyítás nem helyes, sőt maga a tétel sem igaz. Kalmár szükséges feltételt adva a jól interpolálhatósághoz, azt magyar nyelven publikálta (német kivonattal), Fejér tanácsára óvatosan, hogy Fabert se sértse meg nagyon vele.³

Egy másik korai, 1928-ban megjelent dolgozatát manapság a játékelméletben szokták idézni.⁴ Ernst Zermelo német matematikus, a halmazelmélet tudós kutatója adta meg a téma alapját 1912-ben a Cambridge-ben rendezett nemzetközi matematikai kongresszuson, majd 1913-ban egy cikkében. Zermelo olyan játékokra, ahol a lehetséges helyzetek száma véges, egy bizonyítást adott arra, hogy nyerőhelyzetből kiindulva mindig el lehet érni, hogy n lépésben nyerjünk. A bizonyítás azonban hiányos volt, ezt később Kőnig Dénes mutatta meg, aki új bizonyítást adott és általánosította olyan más játékokra is, amelyeknél végtelen sok helyzet lehetséges, de egy-egy helyzetből kiindulva csak véges számú lépés van. Olyan ez, mintha egy végtelen sakktáblán játszanánk, ahol a bástya, a futó és a vezér csak a megszokott hosszúságú lépéseket teheti meg.

Kalmár szintén bekapcsolódott ebbe a kutatásba. A témáról egyébként annakidején Neumann Jánossal is gyakran beszélgetett. Neumann talán halmazelméleti doktori disszertációja miatt is már korán megismerhette Zermelo munkásságát. Kalmár transzfinit számok alkalmazásával bizonyította, hogy minden nyerőhelyzetben van olyan nyerésre vezető taktika, amelynél az, hogy egy adott helyzetben mit kell lépni, csak a helyzettől, és nem a játszma addigi lefolyásától függ. Azt is megmutatta, hogy nyerőhelyzetben mindig van olyan taktika, amely úgy vezet biztos nyerésre, hogy egyben kizárja a helyzetek ismétlődését. Újabban több helyen idézik ezeket a dolgozatokat, viszont elképzelhető, hogy érdemes lenne, akár a Kalmár-hagyaték alapján is a témáról egy új alapos munkát angol nyelven megírni, mivel külföldi kutatók még 2000 utáni cikkükben is panaszkodnak az eredetileg német nyelven írt Kalmár-cikk angol fordítására.⁵

Kalmár már diákkorában nagyon megszerette a számelméletet, érdekelte őt a prímszámok titka. 1927-beli Szegedre kerülése után analitikus számelméletből is jelentek meg írásai. A Dirichlet-sorok együttható-összegének vizsgálata számos számelméleti probléma vizsgálatában (pl. prímszámok eloszlásának kérdésében) hasznos segédeszköz. Kalmár itt új becslésmódot adott, még pedig úgy, hogy az analitikus folytathatóság helyett csak bizonyos egyenlőtlenségeket tett fel és úgy kapta meg az együttható-összegre fennálló becslés szükséges és elégséges feltételét, majd ezt a becslésmódot alkalmazta a prímszámtétel maradéktag-becslésének új bizonyítására.⁶

A factorisatio numerorum problémával kapcsolatosan is jelentek meg írásai, ez a klasszikus partitio numerorum probléma multiplikatív analogonja.⁷ Ha 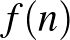jelöli az 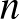természetes szám 1-nél nagyobb egész számok szorzataként való előállításának számát (akárhány tényezőt megengedve és tekintettel a tényezők sorrendjére is), akkor Kalmár aszimptotikát adott meg az 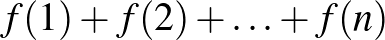értékre, valamint becslést a hibatagra is. Voltak további eredményei ezen a téren (alsó korlátok megadása), amiket egy időben tervezett is megírni, de azok végül elmaradtak. Steven R. Finchnek a Cambridge University Pressnél 2003-ban megjelent Mathematical constants című könyvében egy külön alfejezet szól a Kalmár-féle konstansról, amely a Riemann-féle 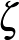függvény használatával a 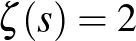egyetlen 1-nél nagyobb valós megoldása (egy 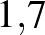és közötti érték) és Kalmárnak itt ebben az előbbi cikkében szerepelt az konstansként.⁸

Kalmárnak volt korai algebrai témájú cikke is,⁹ amelyet Haar Alfréd első- és másodéves hallgatóknak tartott algebra előadásai motiváltak. Haar itt eljutott az algebrai egyenletek Galois-féle megoldhatósági kritériumához, kerülve azonban komplikáltabb csoportelméleti fogalmakat. Kalmár külön dolgozatban mutatott rá, hogy a szokásos alternáló csoport egyszerűségének megmutatása helyett a híres Ruffini–Abel tételhez is el lehet jutni egyszerűbb úton.

Ezeket az eredményeket és cikkeket azért is mutatom, hogy illusztráljam vele az ifjú Kalmár László matematikai sokoldalúságát. Szegedi matematikus professzor főnökei, Riesz Frigyes és Haar Alfréd így aztán kicsit rosszallóan és sajnálkozva látták, hogy Kalmár ezekkel a szép kutatásokkal felhagy azért, hogy aztán matematikai logikával kezdjen el foglalkozni. Riesznek az volt a véleménye, hogy matematikai logikával csak kivénhedt matematikusok foglalkozzanak. Tehát ha már túl van egy matematikus a nagy eredményein és megöregszik, na jól van, akkor filozofáljon, de fiatalembernek ez nem való. Haar azért egy fokkal kicsit jobban vélekedett erről, de amikor Kalmár habilitációjára került sor, ő is megkérdezte tőle, hogy ezen a területen is vannak-e tételek és azokat be is bizonyítják-e?

Az 1928. június 8-án Szegeden készült híres fényképen sok neves matematikusunkat láthatjuk. Ezt a felvételt most azért mutatom, mert ennek van egy képeslap változata is, sok-sok aláírással, ami Riesz Marcel hagyatékából került elő.¹⁰

Az 1928-as szegedi matematikus találkozó résztvevői: Riesz Frigyes, Kerékjártó Béla, Haar Alfréd, Kőnig Dénes, Ortvay Rudolf, Kürschák József, George David Birkhoff, Oliver Dimon Kellogg, Fejér Lipót, Radó Tibor, Lipka István, Kalmár László, Szász Pál. [Képeslap sok aláírással Riesz Marcel hagyatékából.]

Úgy gondolom, hogy Kalmárnak a matematika alapjaihoz, a matematikai logikához való vonzódását két-három személy hatására lehet visszavezetni. Az első a fiatal Neumann János. Még az egyetemi évekből személyesen ismerték egymást, előadásokon volt, hogy egymás mellett ültek és egymásnak csendben kommentálták a hallottakat. Később a matematikusok kávéházában, az Erzsébethíd kávéházban is volt, hogy találkoztak, amikor Neumann éppen Budapesten tartózkodott és Kalmár is éppen ott volt. A matematikai logikáról Kalmár egy Fejér-szeminárium után egy villamos peronján hallott először Neumanntól. Később Neumann akkoriban a Hilbert-féle bizonyításelméletről írt cikkéből is sokat tanult.¹¹

A szegedi Kalmár-hagyaték őriz néhány eredeti Neumann-dokumentumot, így például egy 1946-ban tőle kapott ajánlást: „Körülbelül 1930 óta ismerem Dr. Kalmár Lászlót, ismerem matematikai munkásságát, főleg a formális logikában. Tevékenysége ezen a területen nagyon közel van a saját érdeklődésemhez. Elsőrendű embernek tekintem, és hozzájárulása különösen fontos a logikához. Munkássága az ellentmondás-mentesség és az eldöntésprobléma tárgyakban nagyon érdekes és jelentős. Remélem, kedvező körülmények között folytathatja tudományos munkáját. Lelkes és kiváló tanárként ismerem, aki mindenképpen alkalmas egy egyetemi tanszék vezetésére. Teljes szívből javasolhatom őt bármilyen egyetemi pozícióra a matematikában.” – írta Neumann.

Egy másik nagyon fontos hatás a híres német matematikustól, David Hilberttől eredeztethető, akinek a matematikai logika problémáiról tartott előadását Kalmár 1928-ban Bolognában a Nemzetközi Matematikai Kongresszuson hallgatta. Később személyesen is megismerkedtek, amikor Kalmár elment Göttingenbe egy tudományos kutatási ösztöndíjjal. Itt jegyzem meg, hogy az ösztöndíj elnyerésének hátterében Kürschák József állt, aki nemcsak a pesti, de a vidéki fiatal matematikusokat is figyelemmel kísérte és segítette. Göttingenben Kalmár eljárt Hilbert óráira, sikerült külön beszélnie is vele. Amikor Szegeden már befejeződött a félév, Göttingenben még tartott, ott jobban belenyúlt a nyárba. Kalmár eljárt Emmy Noether és a fiatal Van der Waerden óráira is. Van der Waerden a jegyzeteit ott osztogatta, Kalmár is kapott tőle, amit később beadott a szegedi könyvtárnak, de az már az ő életében állítólag onnan eltűnt. Úgyhogy ha valakinél van Kalmár-féle Van der Waerden előadásjegyzet, akkor azt kérjük, jelezze!

No és hát Landau! Kalmár nagyon szeretett volna vele matematikáról beszélgetni, az óráira is eljárt, de Landau külön nem fogadott senkit. Pedig Kalmár már gimnazistaként tudott Landau prímszámokról írt munkájáról, egyetemistaként levelet is írt Landaunak. Mindenesetre azonban úgy jött haza, hogy közelebbi kapcsolatba nem tudott vele kerülni. Azért is érte meglepetésként, amikor Landau munkatársától, Fencheltől érkezett egy üzenet, amiben az állt, hogy Kalmár megengedi-e Landau professzornak, hogy publikálja éppen készülő könyvében a Grundlagen der Analysisben az ő egyik Bernaysnak tett az aritmetikai alapjaival kapcsolatos megjegyzését. Ennek az volt az előzménye, hogy Hilbert az egyik előadásán Kalmár szerint komplikáltabban bizonyított be valamit, amit ő Neumann cikkéből kiindulva és azt végiggondolva egyszerűbben tudott megmutatni. Bernays ezt elmondta aztán Hilbertnek, és azt Landau is megtudta. Landau könyvének előszavában az áll, hogy habozással áll az olvasók elé a jelen munkával, mert olyan témáról szól, amiről semmiféle új mondanivalója nincs, leszámítva Kalmár egy szóbeli közlését. Mi tagadás, nagy hatással volt ez is a fiatal matematikusra!

Landau emlékezetes sorai a Grundlagen der Analysis (1930) könyvéből.

Kalmár első dolgozata matematikai logikából 1929-ben jelent meg, majd az 1932-es zürichi Nemzetközi Matematikai Kongresszuson már előadást is tartott az eldöntésproblémáról. Kalmár hamarosan a matematikai logika egyik nemzetközi hírű vezető tudósává vált.

Az eldöntésprobléma röviden azt a feladatot jelenti, hogy adjunk meg olyan algoritmust, amellyel tetszőleges logikai formulák azonosan igaz volta eldönthető. Kalmár számos tudományos dolgozatot publikált ezen a területen, bár bizonyos értelemben boldogtalan kincskeresés volt ez, hiszen később kiderült, hogy ilyen algoritmus bizonyíthatóan nem létezik (feltéve persze, hogy az algoritmus intuitív fogalma alatt azt értjük, ahogyan azt ma egzakt módon tárgyalni szokás). Mindenesetre bizonyos speciális formulaosztályokra megoldható az eldöntésprobléma, és bizonyos típusú formulákra Kalmárnak sikerült is azt megoldania. Kalmár legtöbb cikkét az eldöntésprobléma ún. redukció-elméletének szentelte, amikor is az általános problémát visszavezette bizonyos speciális eseteire.

Kalmár sokat foglalkozott Gödel és Church nevezetes tételeinek egyszerűsítésével, általánosításával és helyes interpretáción alapuló népszerűsítésével is. Gödel 1931-ben közölte nagy horderejű eredményét, miszerint minden „valamirevaló” axiómarendszerben (azt, hogy ez mit jelent, persze pontosan meg lehet határozni) megfogalmazható olyan probléma, ami a rendszer keretein belül nem oldható meg, vagyis azt az adott axiómarendszer eszközeivel sem igazolni, sem cáfolni nem lehet. Ez egyben azt is jelenti, hogy nincs olyan abszolút axiómarendszer, amire az egész matematikát fel lehetne építeni, mert akármilyen értelmes axiómarendszert is rögzítenénk, mindig találhatnánk olyan feladatot, amit a rendszer fogalmaival ugyan le tudnánk írni, de semmilyen módon nem tudnánk azt sem bizonyítani sem cáfolni kizárólag csak a rendszer axiómáinak felhasználásával. (József Attila szavaival élve: „a törvény szövedéke mindig fölfeslik valahol”. Ezt 1933–34 telén írta híres versében az Eszméletben.)

Church példát adott algoritmussal egyáltalán meg nem oldható problémaseregekre is, és igazolta, hogy nincs olyan algoritmus, amellyel bármely adott logikai formuláról el lehetne azt dönteni véges számú lépésben, hogy az azonosan igaz-e. Church eredményét népszerűen úgy szokták mondani, hogy vannak abszolúte megoldhatatlan problémaseregek, míg Gödel tétele axiómarendszertől függő, relatíve eldönthetetlen problémák létezésére mutat rá.

Kalmár László előadás közben

Church tételét mélyebbnek gondolták Gödelénél, így meglepő volt, amikor Péter Rózsa észrevette, hogy ez nem így van. Church tétele levezethető a Gödel-tételből, sőt Kalmár azt is igazolta, hogy a Church-tétel egyenesen speciális esete a kellő általánosságban megfogalmazott Gödel-tételnek. Izgalmas területre jutunk akkor, amikor az ún. Church-tézisről (Church–Turing tézisről) gondolkodunk, amelyen Church tétele is alapult. A kérdés tulajdonképpen az, hogy mi is az „algoritmus”. Erről mindenkinek lehet valamiféle intuitív fogalma: egy véges eljárás, amely minden lépésben pontosan előírja, hogy mit kell csinálni. Ha azonban azt akarjuk megmutatni, hogy valamely probléma megoldására egy adott eszközkészlet mellett nincs algoritmus, akkor azt kell bebizonyítani, hogy soha senki nem tud olyan véges eljárást/bizonyítást kreálni, amely megoldaná a feladatot. Az ilyen matematikai bizonyításhoz viszont szükségünk van az algoritmus egzakt definíciójára. Több ügyes kísérlet történt az egzakt definíció megadására, amelyekről végül kiderült, hogy egymással egyenértékű fogalmat eredményeznek, így nagyon is ésszerűnek tűnik, ha az algoritmus intuitív fogalmát a javasolt egzakt fogalmakkal (pl. általános rekurzív függvény, Turing-géppel kiszámítható függvény, stb) helyettesítjük. A Church-tézis azt jelenti, hogy tegyük ezt meg. Persze azt, hogy ezt tényleg jogos megtenni, matematikai szigorúsággal bizonyítani nem lehet, csak ún. plauzibilitási érvekkel lehet alátámasztani.

Kalmár azonban nem igazán hitt abban, hogy a matematika eljárásait valaha is az előbbieknek megfelelő zárt keretek közé lehet kényszeríteni. Nagyon érdekes az, ahogyan véleménye szerint rámutatott arra, hogy a Church-tézis ellen éppúgy lehet plauzibilitási érveket felhozni, mint ahogyan Church mellette hozott fel hasonló érveket. Kalmár egészen meglepő következtetésre jutott: ha valaki elfogadja a Church-tézist, akkor azt is el kell, hogy fogadja, hogy vannak olyan tételek, amelyek ugyan igazak, de azt, hogy igazak, azt semmilyen helyes okfejtéssel soha nem lehet bebizonyítani. Nem csak most nem tudjuk bebizonyítani őket! Soha nem fogjuk! Kalmár szerint, ha valaki hisz abban, hogy a világ törvényei megismerhetők, akkor nem fogadhatja el a Church-tézist, mert szerinte abból azt lehet levezetni, hogy vannak olyan törvényszerűségek, amelyek teljesülnek, de hogy ez tényleg így van, ezt soha senki nem fogja tudni bebizonyítani. Mondhatni egyrészt azért, mert magunk zártuk magunkat zárt keretekbe azáltal, hogy rögzítettük az algoritmus fogalmát. Ez esetleg kellemes lehet, biztonságérzetet adhat, de a megismerésünk korlátoltságával fizetünk majd érte.¹²

Matematikai ars poeticájának is felfoghatók az alábbi sorai:¹³ „megjártam a matematikai egzaktság magasiskoláját s látom, hogy az egzaktságnak nincs határa, nincs olyan precíz módon megfogalmazott definíció, vagy tétel, amibe még precízebb álláspontról bele ne lehetne kötni, mégpedig nemcsak szőrszálhasogatásból és kákáncsomókeresésből, hanem alapos okkal (mert a precízebb álláspont el nem fogadása effektív hibákhoz, hamis eredményekhez vezethet); éppen ezért nem tudom többé statikus-dogmatikusan felfogni a matematikai precízséget: aki ezen innen van, nem precíz, aki túl, az precíz. Ezzel együtt elejtettem persze a matematikának, mint »abszolút igaz tudománynak« a képzetét. Nem írom, hogy kénytelen voltam elejteni, mert az a meggyőződésem, hogy épp az a szép a matematikában, hogy magán viseli az emberi alkotás minden bizonytalanságát. Félre ne érts: létezik számomra is precízség, de nem statikus, hanem dinamikus értelemben: mint precízségre törekvés. Amikor valakit matematikára tanítok, már áll a precízség valamilyen, esetleg nagyon alacsony fokán; magasabbra nem úgy jut, hogy én dogmatikusan magasabb fokra állok és lemarházom, ha ő kevésbé precíz, hanem úgy, ha meggyőzőm arról, hogy érdemes feljebb jönnie. Persze mindezt csak akkor érdemes, ha van benne igény rá; egy cseppet sem baj, ha nincs, akkor maradunk ott, ahol voltunk.”

Zárásképpen egy kapcsolatról szeretnék még röviden szólni. Erdős Pál világhírű matematikus kb. 1500 matematikai dolgozatot írt. Az elsőt cikkét¹⁴ (leszámítva előtte a Középiskolai Matematikai Lapokba írt egy még korábbi írását) Kalmár László segítette megírni. Erdős 18–19 éves korában adott egy új bizonyítást a számelmélet híres Csebisev-tételére (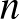 és 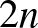közé mindig esik prímszám, ha 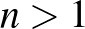).¹⁵ A tárgyalás szabatos bemutatásában azonban akkor még nem volt gyakorlata. Elküldte Szegedre a dolgozatát, majd maga is eljött, Kalmár László segítette neki azt megírni. A világvándor Erdős Pálnak 1931 novemberében ez volt az első matematikai utazása.¹⁶ Kalmárról egyébként azt volt a véleménye, hogy szerinte Kalmár „egy Neumann János kaliberű matematikus volt”, és még azt is mondta, hogy „sokat tanultam a Fejér Lipóttól, de legtöbbet valószínűleg Kalmár Lászlótól”.¹⁷

Lábjegyzetek

¹ Somogyi Károlyné felvétele.

² Kalmárium I–II. Kalmár László levelezése magyar matematikusokkal (Dávid Lajos, Erdős Pál, Fejér Lipót, Grünwald Géza, Kertész Andor, Kőnig Dénes, Rédei László, Rényi Alfréd, Riesz Frigyes, Szele Tibor, Turán Pál, Varga Tamás, Aczél János, Fenyő István, Gyires Béla, Hajós György, Lakatos Imre, Lázár Dezső, Neumann János, Radó Tibor, Surányi János, Szénássy Barna, Szőkefalvi-Nagy Béla, Vincze István). Összeáll. Szabó Péter Gábor, Polygon, Szeged, 2005-08.

³ Kalmár László: Az interpolációról, Math. és Phys. Lapok 33 (1926), 120–149.

⁴ Kalmár László: Zur Theorie der abstrakten Spiele, Acta Sci. Math. 4 (1928), 65–85.

⁵ „However, the translation of Kalmár's paper contains so many mistakes that it is almost impossible to understand what Kalmár did” (Zermelo and the Early History of Game Theory [Schwalbe-Walker, 2001]).

⁶ Kalmár László: Über die Abschätzung der Koeffizientensumme Dirichletscher Reihen, Acta Sci. Math. 4 (1929), 155–181.

⁷ Kalmár László: A „factorisatio numerorum” problémájáról, Mat. és Fiz. Lapok 38 (1931), 1–15.

⁸ Kalmár László: Über die mittlere Anzahl der Produktdarstellungen der Zahlen. I. Acta Sci. Math. 5 (1931), 95–107.

⁹ Kalmár László: Ein Beweis des Ruffini–Abelschen Satzes, Acta Sci. Math. 6 (1932), 59–60.

¹⁰ A matematikus Riesz testvérek. Válogatás Riesz Frigyes és Riesz Marcel levelezéséből. Filep László gyűjtéséből összeállította, az előszót és a bevezető tanulmányokat írta, valamint jegyzetekkel ellátta: Szabó Péter Gábor. Magyar Tudománytörténeti Intézet. Budapest, 2010.

¹¹ Neumann, J. v. Zur Hilbertschen Beweistheorie. Mathematische Zeitschrift 26 (1927), 1–46.

¹² Szabó Péter Gábor: Kalmár László, a számítástudomány hazai úttörője. Alkalmazott Matematikai Lapok 32 (2015), 79–94.

¹³ Kalmár László: Integrállevél. Matematikai írások. Szerk. Varga Antal, Gondolat, Budapest, 1986.

¹⁴ P. Erdős: Beweis eines Satzes von Tschebyschef, Acta Sci. Math. 5 (1932), 194–198.

¹⁵ Kalmár László: Gyertek, bizonyítsuk be Csebisev tételét! I–III, KöMaL 1 (1947–48), 89–90, 127–128, 176–182.

¹⁶ Erdős Pál: Néhány személyes és matematikai emlékem Kalmár Lászlóról, Mat. Lapok, 25. 1974/77, 253–255.

¹⁷ Staar Gyula: A megélt matematika. Beszélgetések, Gondolat, Bp., 1990.