Megoldások, megjegyzések a Héttusa 8. fordulójának feladataihoz

50. Van-e öt olyan egymást követő pozitív egész szám, amelyek legkisebb közös többszöröse négyzetszám?

A válasz: Nincs.

Megoldás. Belátjuk, hogy a keresett öt szám közül legalább két szám négyzetszám.

Ha van öt ilyen szám, azokban a számokban az 5-nél nagyobb prímtényezők mind páros kitevőn szerepelnek, és ez igaz még az 5-re is.

A páros számok egyikében a 2 páros kitevőn van, ezért legfeljebb két olyan páros szám lehet, amelyben páratlan a 2 kitevője.

Legfeljebb egy olyan szám van, amelyben páratlan a 3 kitevője.

Így legfeljebb három olyan szám van az öt szám között, amelynek van olyan prímtényezője, amely páratlan kitevős. A többi számban a prímtényezők mindegyike páros kitevős. Az öt szám között van legalább két olyan, amelyben minden prímkitevő páros, ezek a számok emiatt négyzetszámok. Csak egy olyan számötös van egymást követő számokból, amelyben van két négyzetszám, az 1, 2, 3, 4, 5. Ezek legkisebb közös többszöröse 60, ami nem négyzetszám.

Tehát nincs öt olyan egymást követő pozitív egész szám, amelyek legkisebb közös többszöröse négyzetszám.

Dombi Péter megoldása. Nincs ilyen ötös. Tegyük fel, hogy lenne olyan 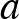$a$ , amelyre

$\displaystyle a,\quad a+1,\quad a+2,\quad a+3,\quad a+4$

legkisebb közös többszöröse négyzetszám. Ekkor az öt szám egyike sem lehet 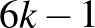$6k-1$ alakú, mert az relatív prím lenne a többi négyhez, és ezért minden prímtényezőjét páros hatványon kellene tartalmaznia, vagyis maga is négyzetszám lenne, márpedig ilyen alakú négyzetszám nem létezik. Tehát a számok között nincs 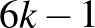$6k-1$ alakú, másképp mondva, 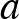$a$ -nak 6-tal oszthatónak kell lennie.

Így viszont a második szám 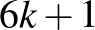$6k+1$ alakú, ami ugyancsak relatív prím lenne a többihez, emiatt négyzetszám lenne.

Megmutatjuk, hogy ekkor az első és a negyedik szám valamelyikének (sőt még az ötödiknek is) szintén négyzetszámnak kellene lennie, ami nyilvánvalóan lehetetlen.

Ugyanis 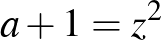$a+1=z^2$ esetén 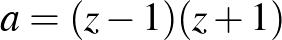$a=(z-1)(z+1)$ , vagyis két egymás utáni páros szám szorzata, ezért a prímtényezős alakjában a 2 biztosan kettőnél nagyobb kitevővel szerepel. A többi szám között más 8-cal osztható nem lehet, így 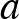$a$ -ban a kettőhatvány kitevő ugyanaz, mint a legkisebb közös többszörösben, vagyis a feltétel szerint páros. De hasonlóképpen páros – méghozzá 0 – a kettőhatvány kitevő 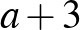$a+3$ -ban is. Mivel a számainkban minden 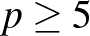$p\ge 5$ prímtényező egyedi, azaz csak egyetlen számban szerepelhet, ezért a 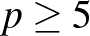$p\ge 5$ prímtényezők biztosan mindenütt páros kitevővel vannak. Végül a 3 kitevője vagy 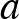$a$ -ban, vagy 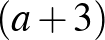$(a+3)$ -ban – amelyikben egynél nagyobb – szintén páros, így az valóban négyzetszám lenne. (Ami az 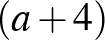$(a+4)$ -et illeti, abban a 2 pontosan második kitevőn szerepel, a 3-at nem tartalmazza, a nagyobb prímek kitevői pedig biztosan párosak.)

Megjegyzés. Erdős Pál 1939-ben bebizonyította, hogy egymást követő pozitív egészek szorzata nem lehet négyzetszám. Az általános állítást – hogy a szorzat nem lehet hatványszám – 1975-ben Erdős és Selfridge igazolta.

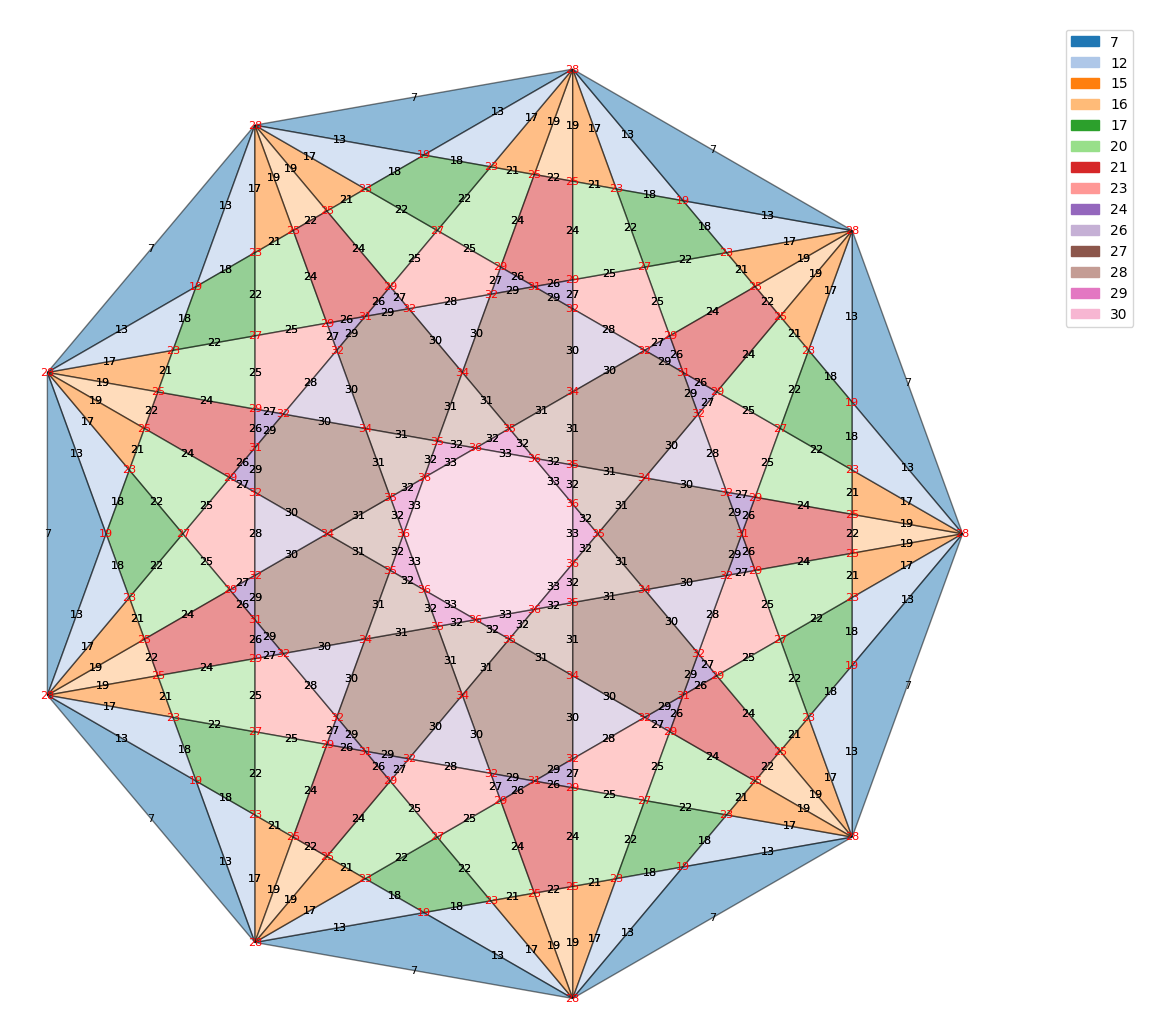
51. Egy konvex kilencszög belsejében felveszünk egy 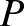$P$ pontot. Tekintsük azokat a háromszögeket, amelyeknek minden csúcsa a kilencszög csúcsai közül való. Legkevesebb hány olyan háromszög van, amely a belsejében vagy a határán tartalmazza a 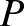$P$ pontot, bárhogyan is vettük fel a kilencszöget és a 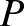$P$ pontot?

A válasz: 7.

Megoldás. Van olyan 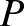$P$ pont, amely legfeljebb 7 háromszög belsejében vagy oldalán helyezkedik el. Legyen a kilencszög négy egymást követő csúcsa 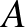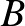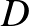$A$ , $B$ , $C$ , $D$ . Válasszunk olyan 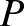$P$ pontot, amely belső pontja az 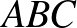$ABC$ és a $BCD$ háromszögnek is. Ez a 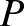$P$ pont csak azoknak a háromszögeknek van a belsejében (vagy a határán), amelyek egyik oldala 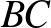$BC$ . 7 ilyen háromszög van.

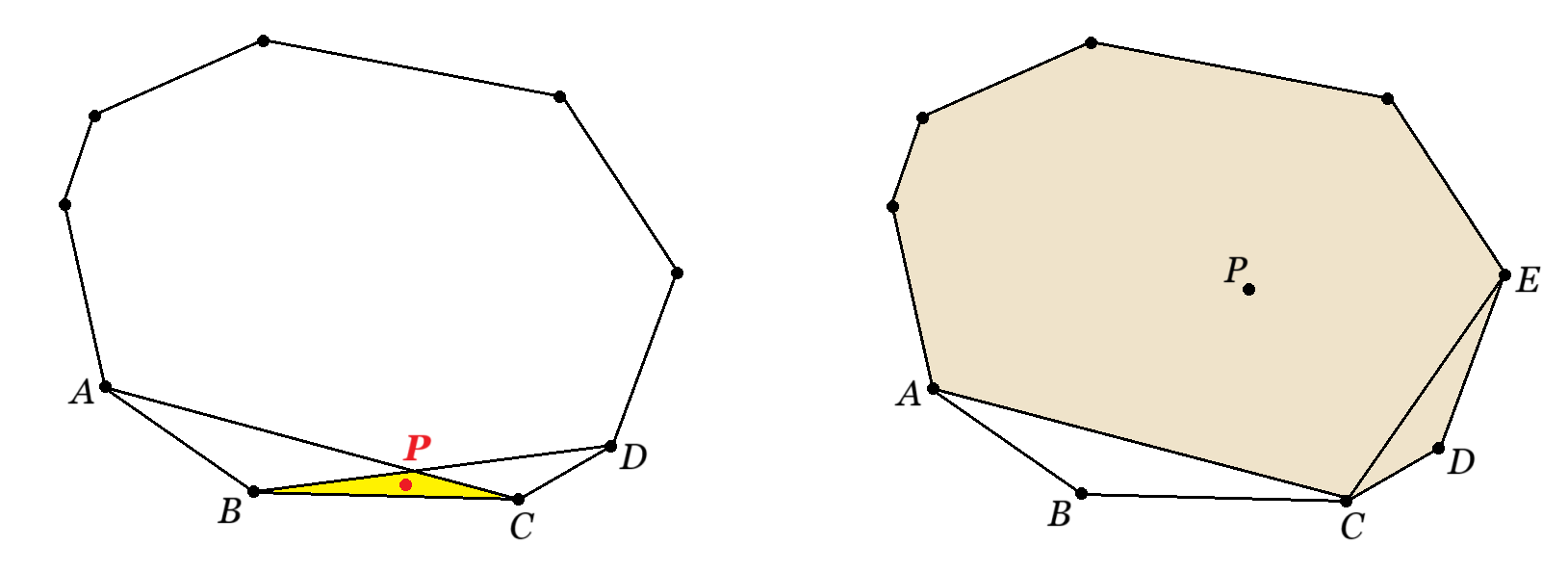
Teljes indukcióval belátjuk, hogy 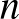konvex $n$ -szög belsejében felvett 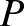$P$ pont legalább 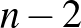$n-2$ háromszögnek belső vagy határpontja.

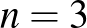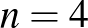Az indukciós feltevés $n=3$ és $n=4$ esetén igaz. Háromszögre nyilvánvaló. Négyszögre könnyen látható, hogy a belsejében lévő 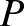$P$ pont legalább két háromszögnek is pontja.

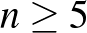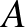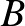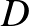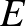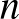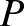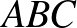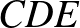Ha $n\ge 5$ , akkor vegyük a sokszög öt egymás utáni csúcsát, az $A$ , $B$ , $C$ , $D$ , $E$ csúcsokat. A konvex $n$ -szög belsejében felvett $P$ pont nem lehet egyszerre az $ABC$ és a $CDE$ háromszög belsejében vagy határán. Feltehetjük, hogy nincs az 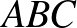$ABC$ háromszög belsejében, és nincs a határán sem. 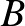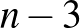Hagyjuk el a $B$ csúcsot a sokszögből, és a megmaradó konvex $(n-1)$ -szögben az indukciós feltevés szerint van $n-3$ olyan háromszög, amelynek pontja a 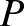$P$ pont. A konvex 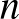$n$ -szöget a 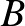$B$ csúcsból húzott átlókkal daraboljuk fel háromszögekre. Ezek közül legalább egy háromszögnek pontja a 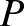$P$ pont. Ez a háromszög különbözik az előbbi 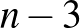$n-3$ háromszögtől. Ezek együtt 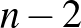$n-2$ olyan háromszöget jelentenek, amelynek pontja a 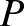$P$ pont.

Tehát egy a kilencszög belsejében felvett 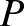$P$ pont legalább 7 háromszögnek pontja, és van is olyan 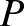$P$ pont, amely csak 7 háromszögnek pontja.

Turchányi Gyula készített egy „térképet”. „… amikor még csak gondolkoztam a feladaton, hogy lássam, merre keressek megoldást, készítettem programmal egy ábrát a szabályos kilencszögre. Nem kevés munkával olyan szép ábrát hoztam létre, hogy megosztásra érdemesnek tartom. Ezen az ábrán a területek belsejét színek kódolják, mellette a magyarázat, hogy az adott szín hány háromszöget jelent; az éleken és csúcsokon (a részek élein és csúcsain) lévő számok pedig azt jelölik, hogy az adott él, pont hány csúcsok alkotta háromszögnek része.”

52. Van-e olyan hétjegyű szám, amely leltározza önmagát? Ezen a következőt értjük: a szám első számjegye egyenlő a szám számjegyei között található 0-k számával, a második számjegye az 1-esek számával, a harmadik számjegye a 2-esek számával, és így tovább, a hatodik számjegye az 5-ösök számával, míg a hetedik számjegye a számban szereplő különböző számjegyek számát mutatja.

A válasz: Igen, van ilyen szám.

Megoldás: Megnézhetjük a hétjegyű számokat, mindegyikről készítünk leltárt, és ha valamelyik leltár visszaadja a leltározott számot, akkor rátaláltunk egy önleltározó számra. Ez számítógép nélkül reménytelen.

Van esély, hogy gyorsan eljussunk egy önmagát leltározó számhoz. Ha felírunk egy tetszőleges hétjegyű számot, erről készítünk egy leltárt, a leltárról is készítek leltárt, újra ismételgetem ezt a lépést, akkor eljuthatok egy fixpontba, ami akkor egy önmagát leltározó szám.

Nézzük meg az eljárást 6, 7 és 8-jegyű számokon:

123456	314159	1234567	1114449	3141592	12345678	31415926
011116	020115	0111117	0300303	0211116	01111118	02111117
140003	221004	1500003	4003002	1410004	16000003	15100004
310114	212014	4101014	4011104	3200203	51000014	42001104
130114	122014	2300203	2300203	3022003	42001104	32102004
130114	122014	3022003	3022003	3022003	32102004	31211005
		3022003	3022003		31211005	23110105
					23110105	23110105
					23110105

Rátaláltunk önmagukat leltározó számokra. Egy ilyen hétjegyű szám: 3022003.

Van-e másik önmagát leltározó hétjegyű szám? A leltározó eljárást az összes hétjegyű számra lefuttatta számítógéppel Makay Géza és Turchányi Gyula. Más eseteket is megvizsgáltak.

A leltározó eljárás a kiinduló számból belefuthat stabil pontba vagy ciklusba, és mindegyik előfordult. Az eljárás hétjegyű számok esetén gyakrabban fut ciklusba, az 1320014 után a 2211105 szám következik, majd újra az előbbi szám, és ebben az esetben nincs is másik ciklus. Összesen két fixpont van: 3022003 és 3103003, és az első önleltározó szám jóval gyakrabban volt végállás a fenti eljárásban, mint a második.

3- és 4-jegyű önleltározó szám nincs, míg 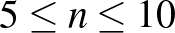$5\le n\le 10$ esetén van 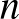$n$ -jegyű önleltározó szám:

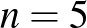$n=5$ esetén 12104,

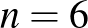$n=6$ esetén 122014 és 130114,

$n=7$ esetén 3022003 és 3103003,

$n=8$ esetén 23110105,

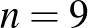$n=9$ esetén 322101005 és 412020004,

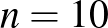$n=10$ esetén 4220110005 és 4301110005.

Nézzünk egy szép megoldást a feladatra, Makay Géza megoldását.

Legyen a hétjegyű számunk az 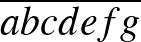$\overline{abcdefg}$ . Ha a szám leltározza önmagát, akkor

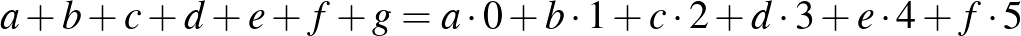
$\displaystyle a+b+c+d+e+f+g=a\cdot 0+b\cdot 1+c\cdot 2+d\cdot 3+e\cdot 4+f\cdot 5$

teljesül.

Mivel a szám hétjegyű, 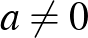$a\neq 0$ kell legyen, így a számban van nem 0 és 0 számjegy is. Ha pontosan két különböző számjegy van, akkor 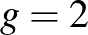$g=2$ , ezért 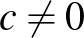$c\neq 0$ , és a feltevés miatt csak 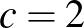$c=2$ lehet, ám a 2020002 szám nem önleltározó.

A 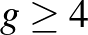$g\ge 4$ eset sem lehetséges. Itt a 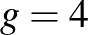$g=4$ esetet írjuk le, hasonló bizonyítás működik 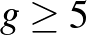$g\ge 5$ -re is.

Két lehetőség van.

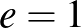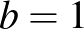(1) Az első hat számjegy között 3 különböző számjegy van, és ezek egyike sem 4, ekkor a 4-esek száma $e=1$ . Ha $b=1$ lenne, akkor a számban volna 2 db 1-es, ami ellentmond ennek, tehát $b\ge 2$ .

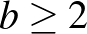A 3 különböző számjegy 0, 1 és 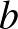$b$ , így a nulla számjegyek száma 1 vagy $b$ .

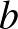Ha 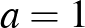$a=1$ , akkor a hat számjegy között van 1 darab 0, 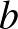$b$ darab 1-es és 1 darab 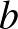$b$ számjegy: 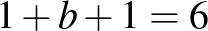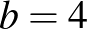$1+b+1=6$ , $b=4$ , amit a mostani feltevésünk kizár.

Ha $a=b$ , akkor a hat számjegy között van 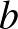$b$ darab 0, 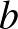$b$ darab 1-es és 1 darab 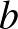$b$ számjegy: $2b+1=6$ , ami láthatóan nem ad megoldást.

(2) Az első hat számjegy között is szerepel a 4-es és még három másik különböző számjegy, mondjuk a 0, 1 és 2. Ekkor a számjegyek között valamelyikből 4 darab van, a többiekből rendre legalább 2, illetve 1 darab. Eddig háromféle számjegyet számoltunk össze, ezekből van 7, és a negyedik számjegy miatt már 8 lenne a számjegyek száma.

Így csak a 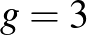$g=3$ eset maradt. Az első hat számjegyben szerepelhet a 0, a 3 és még egy számjegy. A 0, 1, 2, 3, 4, 5 számjegyekből három nem szerepel, őket 3 darab 0 leltározza, tehát 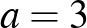$a=3$ . Ebből következik, hogy 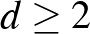$d\ge 2$ , és hogy nem lehet 4-es és 5-ös számjegy. Kipróbálva a lehetséges 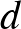$d$ -ket, a következő megoldásokat kapjuk:

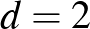$d=2$ : 3022003, önleltározó,

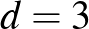$d=3$ : 3103003, önleltározó,

és ez az összes megoldás.

Nézzük Dombi Péter szellemes megoldását.

Igen, két ilyen tulajdonságú szám van, a 3022003 és a 3103003. Először is vegyük észre, hogy az első hat számjegy összege 7 kell, hogy legyen. Ezek után tekintsük át a lehetőségeket úgy, hogy csak az első számjegyet – a nullák számát – „vesszük komolyan”, a többit csak nagyság szerint és „szerep nélkül” soroljuk fel, arra figyelve, hogy a hat számjegy összege 7 legyen. Az első számjegyet vastagítva jelezzük, amit az alábbi néhány módon lehet a kellő számú összeadandóval 7-re kipótolni:

a) 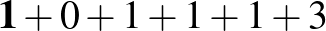$\mathb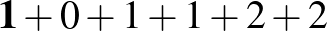f{1}+0+1+1+1+3$

b) $\mathbf{1}+0+1+1+2+2$

c) 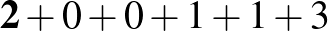$\mathbf{2}+0+0+1+1+3$

d) 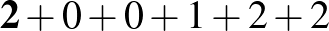$\mathbf{2}+0+0+1+2+2$

e) 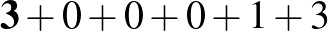$\mathbf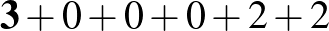{3}+0+0+0+1+3$

f) $\mathbf{3}+0+0+0+2+2$

g) 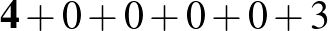$\mathbf{4}+0+0+0+0+3$

Az a)-beli számjegyekkel nem lehet megfelelő számot előállítani, hisz ott négy 1-es van, míg a multiplicitások (0, 1, 3) mind 4-nél kisebbek. Hasonlóan, a b)-nél három darab 1-es, a d)-nél három darab 2-es van, de a multiplicitások (0, 1, 2) 3-nál kisebbek. A g) is ránézésre kizárható, mivel a 3 nem lehet semelyik számjegy multiplicitása. Végül a c) esetben pontosan két 1-es lenne a számban (a hetedik jegy is nyilván 1-estől különböző), de olyan 2-es nincs a számjegyek között, ami az 1-es multiplicitása lehetne.

Maradt az e) és az f) elrendezés, amelyeknél az e)-ből egyből adódik a 3103003, az f)-ből pedig a 3022003 szám.

Megjegyzés. Ezzel a módszerrel könnyen találhatunk nemcsak hétjegyű, de egyéb hosszúságú önleltározó számokat is:

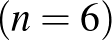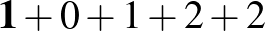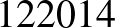$\displaystyle (n=6)$	$\displaystyle \mathbf{1}+0+1+2+2$	$\displaystyle \Longrightarrow$	$\displaystyle 122014$
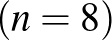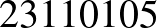$\displaystyle (n=8)$	$\displaystyle \mathbf{2}+0+0+1+1+1+3$	$\displaystyle \Longrightarrow$	$\displaystyle 23110105$
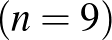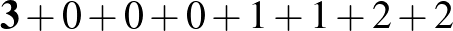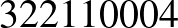$\displaystyle (n=9)$	$\displaystyle \mathbf{3}+0+0+0+1+1+2+2$	$\displaystyle \Longrightarrow$	$\displaystyle 322110004$
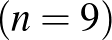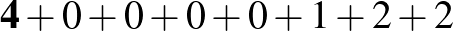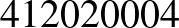$\displaystyle (n=9)$	$\displaystyle \mathbf{4}+0+0+0+0+1+2+2$	$\displaystyle \Longrightarrow$	$\displaystyle 412020004$
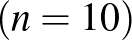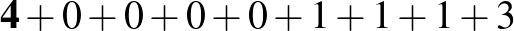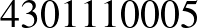$\displaystyle (n=10)$	$\displaystyle \mathbf{4}+0+0+0+0+1+1+1+3$	$\displaystyle \Longrightarrow$	$\displaystyle 4301110005$
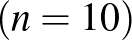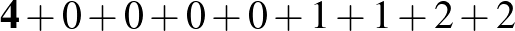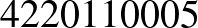$\displaystyle (n=10)$	$\displaystyle \mathbf{4}+0+0+0+0+1+1+2+2$	$\displaystyle \Longrightarrow$	$\displaystyle 4220110005$

Az önleltározó számmal rokon az önleíró szám:

https://en.wikipedia.org/wiki/Self-descriptive_number

Volt már a feladathoz hasonló kérdés a KöMaL-ban:

http://db.komal.hu/KomalHU/feladat.phtml?id=54292

53. Írjuk be az 1, 2, 3, …, 64 számokat egymás után egy 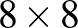$8\times 8$ -as táblázat mezőibe úgy, hogy az egymás után beírt számok mindegyike az előző számmal oldalszomszédos mezőbe kerüljön. Legfeljebb mekkora lehet a főátlóba beírt nyolc szám összege?

A válasz: 432.

Megoldás. Van olyan kitöltés, amikor a főátlóban a számok összege 432, a főátlón a 26, 52, 54, 56, …, 64 számokkal. Az ábrán kígyózó kitöltésben a sakkban szokásos jelölésekkel a számok beírását az a1 mezőn (a kék vonalon) kezdjük, és a g2 mezőn fejezzük be. A főátló számai 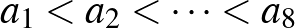$a_1<a_2<\cdots <a_8$ .

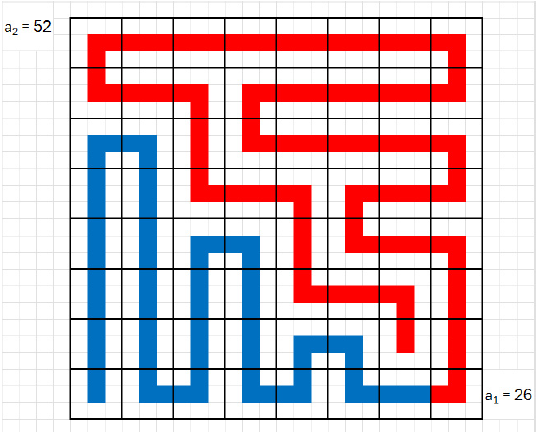
Ha a táblázat mezőit sakktábla módjára színezzük fehérre és feketére, akkor két szomszédos szám különböző színű mezőkbe kerül, ezért az azonos színű mezőkbe ugyanolyan paritású számokat írunk. A főátlón lévő mezők azonos színűek, így az ott álló számok vagy mind párosak, vagy mind páratlanok.

A főátlóban lévő legkisebb szám legyen 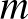$m$ . Ekkor a nála kisebb számok mind a főátló egyik oldalán helyezkednek el. A főátló két háromszögre bontja a táblát, mindkét oldalon 28 mező van, ezek közül 16 fehér, 12 fekete, vagy fordítva. A számok beírásakor váltakozó színű mezőkbe írjuk a számokat, ezért a főátlóra lépés előtt legfeljebb 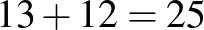$13+12=25$ lépést tehetünk, így a főátlón felbukkanó legkisebb szám 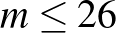$m\le 26$ . Ezért a főátlóban álló számok nem nagyobbak a 26, 52, 54, 56, 58, 60, 62, 64 számoknál. A fenti kitöltés éppen ilyen.

Dombi Péter is belátja, hogy az átlós összeg 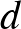$d$ értéke legfeljebb 432, amiből következtet arra, hogy 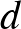$d$ minimális értéke 88.

Az előbbi ábrán kígyózó kitöltésben a sakkban szokásos jelölésekkel a kígyó feje az a1 mezőn, a farka a g2 mezőn van. Ha ellenkező irányban, a „farkától a fejéig” számozzuk, akkor az 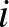$i$ -edik mezőn 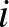$i$ helyett 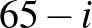$65-i$ áll, ezzel az átlóban a korábbi 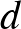$d$ összeg 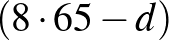$(8\cdot 65-d)$ -re, azaz 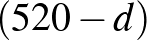$(520-d)$ -re változik. Így kapjuk a maximális 432 összegből a minimális átlós összeget, 88-at.

Belátja azt is, hogy az átlós összeg 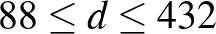$88\le d\le 432$ értéke bármilyen páros szám lehet, kivétel a 90 és a 430.

A táblába sokféle úton beírhatók az 1, 2, …, 64 számok. Most olyan bejárást keres, aminél a kígyó feje és farka szomszédos mezőn van, így a kígyó kört (Hamilton-kört) alkot. Ennek a trükknek az lesz az előnye, ha a körön a számozást 1-gyel későbbi mezőn kezdi, akkor minden átlós mezőt 1-gyel korábban ér el, vagyis 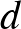$d$ értéke éppen 8-cal fog csökkenni.

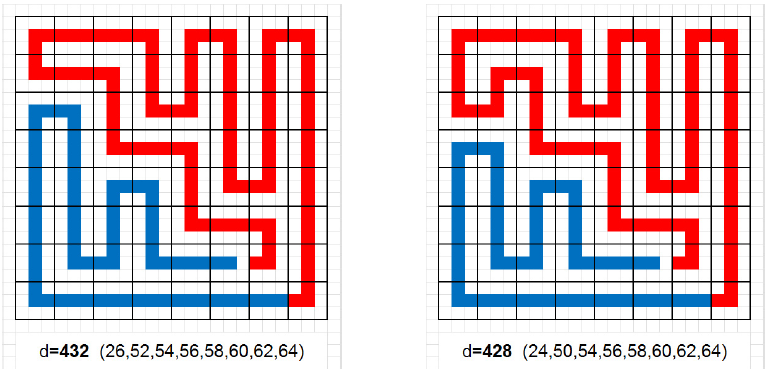
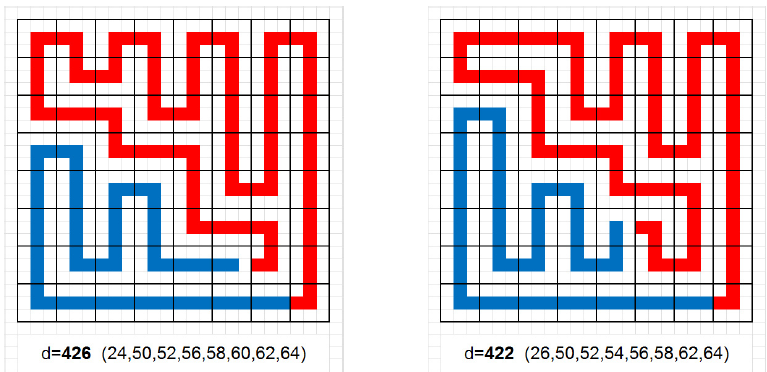
Vizsgálja a feladatot 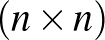$(n\times n)$ -es táblázatra, meghatározza a maximális átlós összeget is. Az ábra mutatja 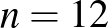$n=12$ -re és 13-ra a maximumot adó kitöltést (a kitöltés a bal alsó sarokból indul).

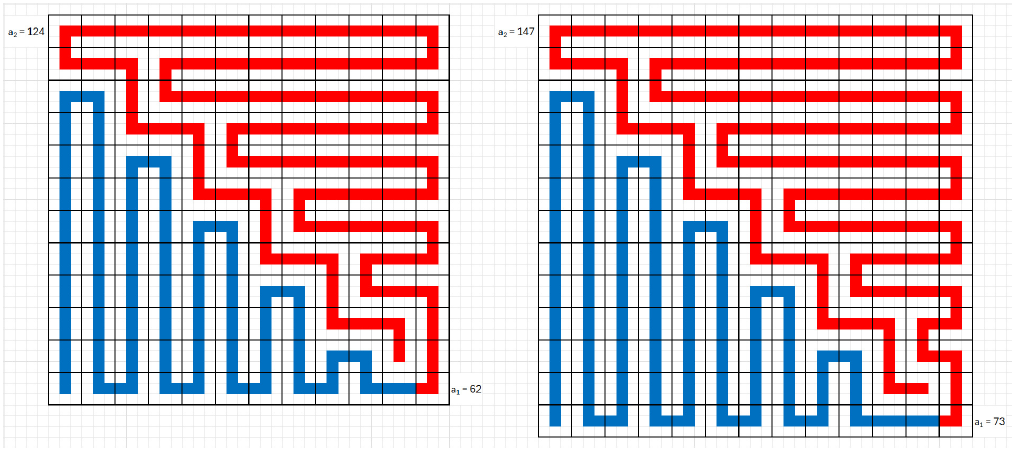
A mintázat gond nélkül kiterjeszthető tetszőleges 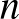$n$ -re.

54. Az asztalra 8 különböző zsetont tettünk le egy sorba. Rendezzük őket fordított sorrendbe úgy, hogy egy lépésben vagy két szomszédos zsetont cserélünk meg, és ezért fizetünk 1 tallért, vagy két olyan zsetont cserélünk fel ingyen, amelyek között pontosan 3 zseton helyezkedik el. Legkevesebb hány tallért kell fizetnünk az átrendezésért?

A válasz: 4 tallért.

Megoldás. Számozzuk meg a zsetonokat az 1, 2, 3, …, 8 számokkal. Figyeljük meg a zsetonok helyének paritását. Az átrendezés után minden zseton más paritású helyre kerül (a páratlan helyekre kerülnek a páros számok, és a páros helyekre a páratlanok).

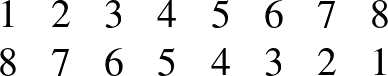
$\displaystyle \begin{matrix} 1&2&3&4&5&6&7&8\\ 8&7&6&5&4&3&2&1 \end{matrix}$

Az ingyenes cserék nem változtatják meg a zsetonok helyének paritását, csak a fizetős cserék. Egy csere 2 zseton paritásán változtat, így a 8 zseton paritásának megváltoztatásáért legalább 4 tallért fizetni kell.

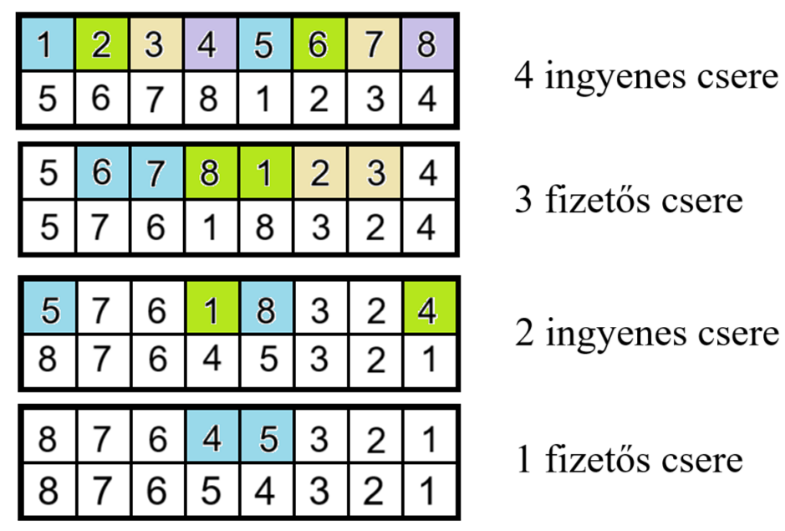
(Az azonos színű számokat felcseréltük.)

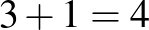$3+1=4$ tallér kifizetésével megcserélhető a zsetonok sorrendje.

55. Egy királyságban a kancellár és a 33 fős kancellária testületében mindenkinek egy-egy tallér a fizetése. A fizetések módosulnak, ha a kancellár erre javaslatot tesz, és azt a testület szavazással elfogadja. Mindenkinek a fizetése csak egész számú tallér lehet, és a fizetések összege mindig 34 tallér. Ha több szavazat van a javaslat mellett, mint ellene, akkor azt elfogadják. A kancellár nem szavazhat, csak a testület 33 tagja. Egy szavazó igennel szavaz, ha a javaslat növeli a fizetését, és nemmel szavaz, ha csökkenne a fizetése. Ha a fizetése az előző fizetéséhez képest nem változik, akkor tartózkodik a szavazástól. A kancellár naponta tehet egy újabb javaslatot.

A kancellár eléggé önző, és ugyanakkor okos is. Mekkora a legnagyobb fizetés, amit megszerezhet magának a kancellár?

A válasz: 31 tallér.

Megoldás. Két szempontot követnek a javaslatok. A kancellár átmenetileg lemond a fizetéséről, így nagyobb a mozgástere, hogy a szavazásoknál megkapja a többséget. Továbbá minden javaslatával közel a felére csökkenti a fizetett testületi tagok számát. A végső javaslat majd elveszi a megmaradt fizetett tagoktól a pénzt, mert olcsón „szavazatokat vásárolhat” a fizetés nélküliek köréből.

Az első javaslat 17 főnek a fizetését megduplázza, és a többiek nem kapnak fizetést. A javaslatot 17 igen és 16 nem szavazattal elfogadják. (17-en kapnak fizetést.)

A második javaslat 9 fő fizetését 2 tallérról 3 vagy 4 tallérra emeli, és 8 főtől elveszi a 2 talléros fizetést. A javaslatot 9:8 arányban elfogadják. (9-en kapnak fizetést.)

A harmadik javaslat után már csak 5 fő kap fizetést. A negyedik szavazás után 3 fő, az ötödik szavazás után már csak 2 fő kap fizetést.

A kancellár a hatodik napon lekenyerez három fizetés nélkül dolgozót 1-1 tallérral, és a megmaradó 31 tallér lesz majd a kancellár saját fizetése. Ezt a javaslatot 3:2 arányban elfogadják. (És a hetedik napon megpihen …)

Mivel a kancellár nem tudja elérni azt, hogy valamelyik szavazási kör után csak egyetlen fizetett testületi tag maradjon, ezért az utolsó körben van legalább 2 fizetett fő, akik nemmel szavaznak a fizetésük elvesztésére, emiatt kell 3 igen szavazat, ami legalább 3 tallér. 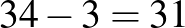$34-3=31$ tallérnál nagyobb fizetést nem szavaznak meg a kancellárnak.

Koncz Levente indoklása arra, hogy a kancellár legfeljebb 31 tallért tud megszerezni.

Amikor utoljára növeli a fizetését, akkor legalább egyvalakinek csökken, tehát kell legalább két igen szavazó, akinek rajta kívül nő a fizetése. Ezért 1-1 tallér mindenképp „kint marad”. Ha 32-t meg tudna szerezni, az csak úgy volna lehetséges, ha előtte minden „kint levő” tallér egy kézben lenne, ami lehetetlen: mindig kell hogy legyen két olyan szavazó, akinek nem 0 a fizetése. Ha csak egy lenne, akkor az utolsó előtti pozitív fizetésű szavazó fizetésének nullára csökkentéséhez nem lett volna meg a két igen szavazat.

56. Egy 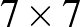$7\times 7$ -es táblázat celláiból hányféleképpen választhatunk ki 15 cellát úgy, hogy azoknak ne legyen közös pontja? (Azaz semelyik két cellának se legyen közös csúcsa vagy közös oldala.)

A válasz: 64

Megoldás. A 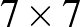$7\times 7$ -es táblázat celláiból egyféleképpen választhatunk 16 cellát úgy, hogy azoknak nincs közös pontja. A táblát felosztottuk 16 tartományra és a kiválasztott cellákat befestettük kékre.

Egy tartományból legfeljebb egy cellát választhatunk. A 4 cellából álló tartománynak választhatjuk bármelyik celláját: a befestett helyzetűt, legyen ez az alaphelyzet (A); a felső cellát (F); a jobb oldalit (J); vagy a jobb felső sarokban levőt (S).

Ha mind a 15 kiválasztott cella alaphelyzetben van, akkor egy tartomány üresen marad, onnan nem választottunk. Ez 16 lehetőség.

(1) Ha valamelyik tartományban a kiválasztott cella felső helyzetű, akkor a felette lévő tartományokban a kiválasztott cella is felső helyzetű, majd következik egy üres tartomány, és a következő tartományok alaphelyzetűek. Ugyanez igaz akkor is, ha a 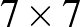$7\times 7$ -es tábla jobb szélén a 2 cellából álló tartományok egyikében a felül lévő cellát választjuk.

(2) Ha valamelyik tartományban jobb oldali a kiválasztott cella, akkor a tőle jobbra sorakozó tartományokban is jobb oldali helyzetű a kiválasztott cella, majd jön egy üres tartomány, és a következő tartományok alaphelyzetűek. Ugyanez igaz akkor is, ha a 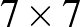$7\times 7$ -es tábla felső sorában a 2 cellából álló tartományok egyikében a jobb szélső cellát választjuk.

Nem választhatunk egy tartományban S helyzetű cellát, mert akkor a felette lévő tartományok egyike üres, és a tőle jobbra lévő tartományok közül is üres az egyik. Azonban csak egy üres tartomány lehet. Nem lehet az sem, hogy a kiválasztottak között van F, és van J helyzetű cella is.

Az (1) esetben kiválasztjuk a tartományok oszlopának egyikét, és abban az oszlopban azt a legalsó tartományt, amelyben F helyzetű a kijelölt cella, és kiválasztjuk az üresen maradó tartományt. A lehetőségek száma 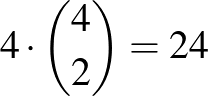$4\cdot \binom{4}{2}=24$ . Ehhez hasonlóan a (2) eset is 24 lehetőséget ad.

A 15 cella kiválasztása tehát 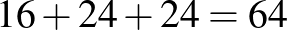$16+24+24=64$ -féleképp történhet.

Koncz Levente vázlatos indoklása:

Az világos, hogy 16 cellát egyféleképpen lehet kiválasztani. Az így kiválasztható 16 cellából bármelyiket elhagyhatjuk, ez 16 jó kiválasztás.

Keressük még azokat a kiválasztásokat, amelyekben van olyan kiválasztott cella, ami nincs a fenti 16 között. Könnyű meggondolni, hogy egy ilyen konstrukcióban vagy 3 sorban ki van választva 4 cella, és egy negyedik sorban 3, vagy pedig 3 oszlopban van kiválasztva 4 cella, és egy negyedik oszlopban 3. Azt is könnyű meggondolni, hogy egy sorból (vagy oszlopból) 3 cellát 6-féleképpen lehet úgy kiválasztani, hogy ne legyen mindhárom kiválasztott cella a fenti 16 között. 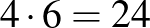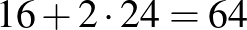Ez a „soros” és az „oszlopos” kiválasztások esetén is $4\cdot 6=24$ lehetőség, az összes megfelelő kiválasztások száma ezért $16+2\cdot 24=64$ .

Dombi Péter megoldása:

A 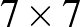$7\times 7$ -es táblázat celláiból 64-féleképpen választhatunk ki 15 ilyen cellát (a cellaválasztást egyszerűen bábuk – sakknyelven egymást nem támadó királyok – elhelyezésével is kifejezhetjük). Megfelelő elrendezést a következőképpen kaphatunk. Tekintjük azt az egyetlen felállítást, ami 16 bábuval elérhető, majd ebből tetszőlegesen elhagyunk 1-et. Ilyenből nyilván 16 van, egy látható a bal oldali ábrán. Ezeken kívül még az is megfelelő, ha egy-egy ilyen állásnál kiválasztjuk a hiányos sort vagy oszlopot, és abban a vonalban az ottani 3 bábut elmozgatjuk úgy, hogy továbbra se kerüljön 2 egymás mellé. Ez tulajdonképpen a feladat egydimenziós változata, 7 mezőn 3 bábuval, itt a lehetőségek száma 10 (hogy miért, arra később visszatérek). 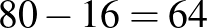A 8 lehetséges vonalra így 80 felállás adódik, de éppen az előrebocsátott 16 helyzetet kétszer is számba vettük, egyszer sor- és egyszer oszlopirányban, vagyis az egy-egy vonalban „elrontott”, különböző állások száma $80-16=64$ .

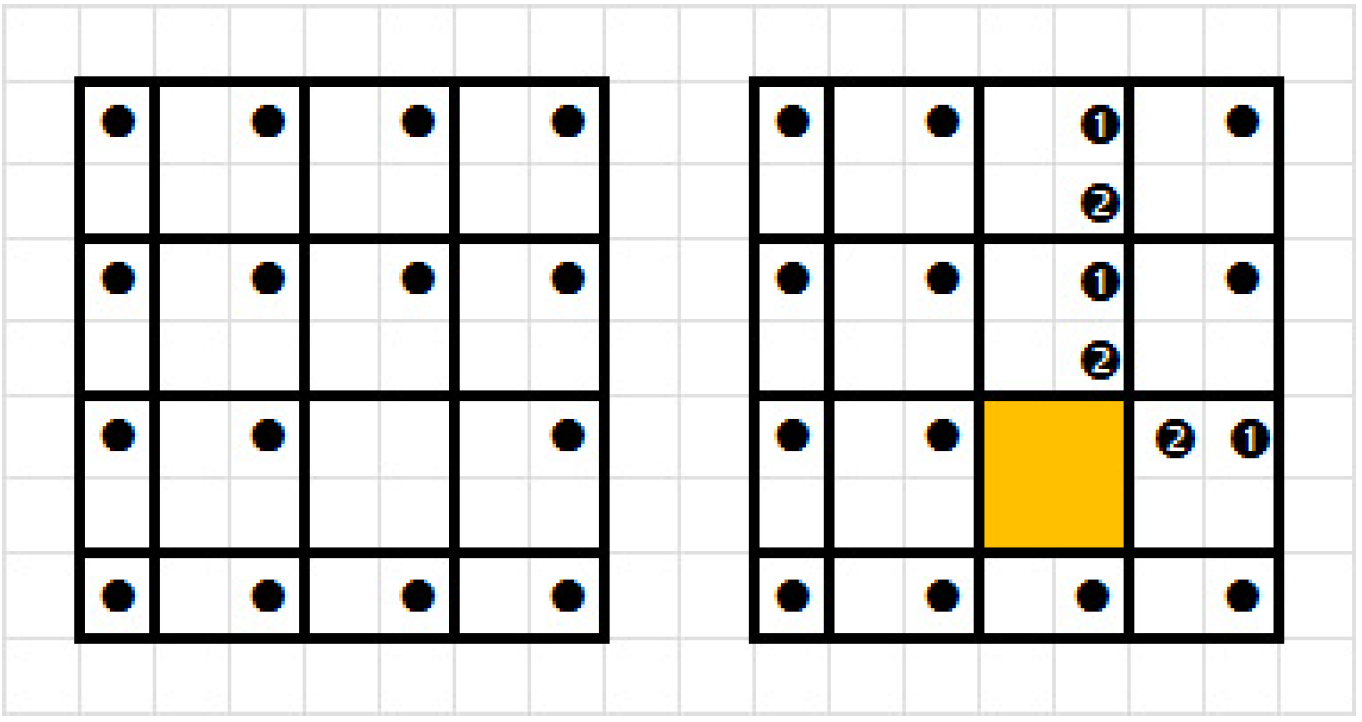
Meg kell még mutatni, hogy minden keresett helyzet ilyen, azaz egyetlen „elrontott” vonalat leszámítva „teljesen szabályos”. Tekintsünk egy, a feladatnak megfelelő állást. Osszuk fel a táblát az ábra szerint 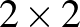$2\times 2$ -es, illetve a szélen 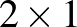$2\times 1$ -es lapokra. Mivel 15 bábu van, ezért 1 kivétellel minden lap pontosan 1 bábut fog tartalmazni. Bár nincs érdemi különbség, de először tegyük fel, hogy valamelyik 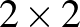$2\times 2$ -es lap maradt üresen. Ekkor a szélső „dominókon” biztosan az ábra szerinti helyzet jön létre (a szomszédos lapokon a bábuk lapon belüli kényszerhelyzetét azzal lehet érzékeltetni, mintha ezek azonos töltésű mágnesek lennének).

Legyen A egy olyan lap, amelyik nincs az üres lappal egy vonalban. Ezen a bábu akadálytalanul „látja” a vele sorban és egy oszlopban levő dominó bábuját, és mivel a szélső dominók bábui – a sarok miatt – nyilván rendezettek, ezért ezektől egyesével haladva A irányába az A-beli bábunak is rendezettnek – jobb felső cellásnak – kell lennie.

Ha A az üres lappal egy vonalban, például felette található, akkor az A-beli báburól csak annyi állítható, hogy a lap jobb oldalán, tehát az üres lap alatti rendezett bábuvonalban lesz, de esetleg a lap alsó cellájában. Hasonlóan, az üres laptól jobbra eső A lapban a bábu a felső sorba kényszerül ugyan, de kerülhet a bal oldali cellába is. Fontos észrevenni, hogy egy „mutáns” A laptól az üres lap felé haladva minden lapnak mutánsnak kell lenni, ezért nem lehet egyszerre az üres lap sorában is és oszlopában is mutáns lap, mert akkor az üres lap felső és jobb oldali szomszédja mindkettő mutáns lenne, és ez szomszédos bábupozíciót eredményezne (az ábrán (2)-es jellel).

Ugyanezzel a gondolatmenettel intézhető el az az eset is, amikor az üres lap a bal alsó sarokmező, vagy egy szélső „dominó”. Ezzel beláttuk, hogy 15 bábus megfelelő állást csak úgy kaphatunk, ha egy szabályos 15-ös állásnak valamelyik sorát vagy oszlopát – a feltételt megtartva – átrendezzük.

Megjegyzések. Dombi Péter bizonyítja az általános esetet is, hogy 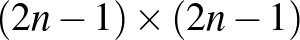$(2n-1)\times (2n-1)$ -es táblázatból 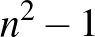$n^2-1$ közös pont nélküli cella kiválasztására 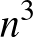$n^3$ különböző lehetőség van.

Feltehetjük a következő kérdést is: Hányféleképp választhatunk a 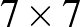$7\times 7$ -es táblán a feltétel szerint 14 cellát?

Információk

Főmenü

Megoldások, megjegyzések a Héttusa 8. fordulójának feladataihoz