„Møbee Twin”

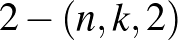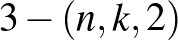„Møbee Twin” avagy konstrukciók és blokkrendszerekre

Blokkrendszerek és duálisaik

Tavalyelőtt került piacra a Møbee nevű kártyajáték, aminek a szabálya nagyon egyszerű, egymondatos: Csapj fel három lapot a pakliból és keresd meg azt az egyetlen figurát, amelyik mindhármon szerepel! A leggyorsabb játékos nyeri a kört. Az ilyen paklik gyártásához szükséges kombinatorikai struktúrákat, a 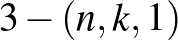$3-(n,k,1)$ blokkrendszereket tárgyalja a szerző korábbi [5] cikke. 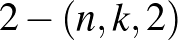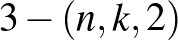Jelen cikkben $2-(n,k,2)$ és $3-(n,k,2)$ blokkrendszerekre adunk konstrukciókat. Az utóbbi blokkrendszerekből „Møbee Twin” paklik gyárthatók, ahol minden lapon ugyanannyi figura szerepel és bármely három lapon pontosan kettő azonos közöttük. A könnyebb érthetőség érdekében a legfontosabb fogalmakat, tételeket újratárgyaljuk.

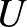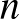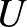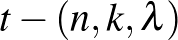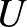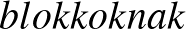1. Definíció. Legyen $U$ nemüres, $n$ -elemű halmaz. Az $U$ feletti $t-(n,k,\lambda)$ blokkrendszer alatt $U$ olyan kitüntetett $k$ -elemű részhalmazainak (amelyeket $blokkoknak$ nevezünk) halmazát értjük, amire teljesül, hogy 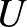$U$ bármely 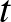$t$ különböző elemét választva mindig éppen 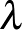$\lambda$ olyan blokk van, ami mindegyiket tartalmazza.

Az első természetes kérdés, hogy mely paraméterek esetén léteznek ilyen 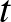$t$ -blokkrendszerek. A kérdésre a részleges választ, pontosabban 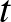$t$ számú szükséges feltételt ad az alábbi tétel:

1. tétel. (Oszthatósági feltételek) Ha létezik 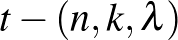$t-(n,k,\lambda)$ blokkrendszer, akkor teljesülnek az alábbi oszthatóságok:

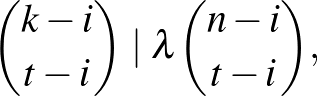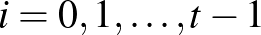$\displaystyle \binom {k-i}{t-i} \mid \lambda \binom {n-i}{t-i},$ ahol $i=0,1,\dots,t-1$ .

A bizonyítás egyszerűen elvégezhető, elegendő rendre a blokkok számát, egy rögzített 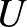$U$ -beli elemet tartalmazó blokkokat, egy rögzített 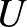$U$ -beli elempárt tartalmazó blokkokat, illetve egy rögzített 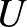$U$ -beli elemhármast tartalmazó blokkokat, stb. összeszámolni és felhasználni, hogy az eredményül kapott törtek mind egészek.

A 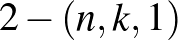$2-(n,k,1)$ blokkrendszerekre általános konstrukciók adhatók véges projektív és véges affin síkok segítségével, részletesen lásd például [1],[2],[4]. A 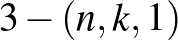$3-(n,k,1)$ blokkrendszerek véges geometriai, Möbius-síkokat használó konstrukcióit részletesen tárgyalja [5].

A továbbiakban feltételezzük, hogy 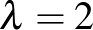$\lambda =2$ . Megjegyezzük, hogy míg a 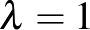$\lambda =1$ -re végtelen sok különböző blokkrendszert ismerünk, ez nem igaz a 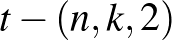$t-(n,k,2)$ -re, ugyanis ez esetben egyelőre csak véges listával rendelkezünk.

Kiindulva egy 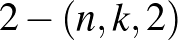$2-(n,k,2)$ blokkrendszerből, illetve egy 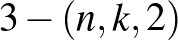$3-(n,k,2)$ blokkrendszerből, az első esetben természetes módon tudunk gyártani olyan 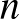$n$ -lapos „Dobble” paklit, ahol minden lapon ugyanannyi figura szerepel és bármely két lapon pontosan kettő azonos közöttük, a másik esetben pedig egy 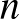$n$ -lapos „Møbee Twin” paklit, ahol szintén minden lapon ugyanannyi figura szerepel és bármely három lapon pontosan kettő azonos közöttük (de bármely kettő lapon kettőnél több közös figura is szerepel). Legyenek ugyanis a pakli lapjai az 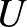$U$ elemei, a figurák pedig a blokkrendszer blokkjai. Egy figura pontosan akkor szerepeljen egy lapon, ha a neki megfelelő blokk tartalmazza a lapnak megfelelő 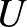$U$ -beli elemet. Az így kapott „Møbee Twin” pakli lapjainak száma tehát 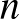$n$ , a felhasznált figurák száma 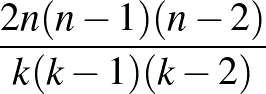$\frac{2n(n-1)(n-2)}{k(k-1)(k-2)}$ , az egy lapon szereplő figurák száma pedig 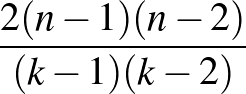$\frac{2(n-1)(n-2)}{(k-1)(k-2)}$ . Két lapon a közös figurák száma éppen 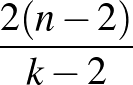$\frac{2(n-2)}{k-2}$ és minden figura $k$ lapon fordul elő. (Ezeket az értékeket kaptuk, amikor a fenti oszthatósági feltételeket bizonyítottuk.)

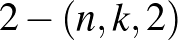blokkrendszerek

Először vizsgáljuk a 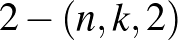$2-(n,k,2)$ blokkrendszereket 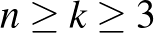$n \geq k\geq 3$ feltételekkel.

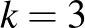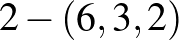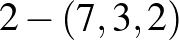Nézzük a $k=3$ esetet. Az oszthatósági feltételek szerint a legkisebb lehetséges, nemtriviális megoldások a $2-(6,3,2)$ és $2-(7,3,2)$ blokkrendszerek. Ezekre mutatunk egy-egy elemi konstrukciót a következőkben.

$2-(6,3,2)$ :

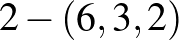Legyen 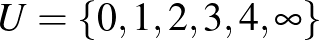$U=\{0,1,2,3,4,\infty\}$ , a blokkok (összesen 10) pedig kétfélék:

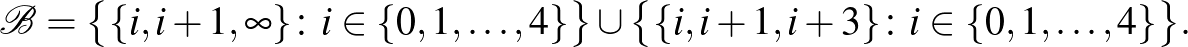
$\displaystyle \mathcal{B}=\bigl\{\{i,i+1,\infty\}\colon i \in \{0,1,\dots,4\}\bigr\}\cup \bigl\{\{i,i+1,i+3\}\colon i \in \{0,1,\dots,4\}\bigr\}.$

A konstrukcióban az összeadást mod 5 értjük. Ha a két kiválasztott 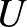$U$ -beli elem egyike sem a 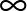$\infty$ , akkor amennyiben nem 1-gyel térnek el (mod 5), akkor a második típusú blokkok közül pontosan 2 tartalmazza őket, ha szomszédosak, akkor pedig az első típusú és a második típusú blokkok közül is 1-1 felel meg. Ha a kiválasztott két elem közt ott van 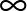$\infty$ is, akkor pontosan 2 első típusú, mindkét elemet tartalmazó blokk van.

$2-(7,3,2)$ :

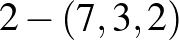Legyen 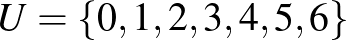$U=\{0,1,2,3,4,5,6\}$ , a blokkok (összesen 14) pedig kétfélék:

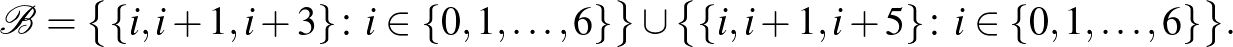
$\displaystyle \mathcal{B}=\bigl\{\{i,i+1,i+3\}\colon i \in \{0,1,\dots,6\}\bigr\}\cup \bigl\{\{i,i+1,i+5\}\colon i \in \{0,1,\dots,6\}\bigr\}.$

A konstrukcióban az összeadást itt mod 7 értjük. Megjegyezzük, hogy külön tekintve, az első típusú blokkok épp egy Fano-sík egyeneseinek megfelelő blokkok és ugyanez igaz a második típusú blokkokra is.

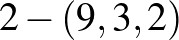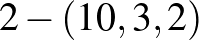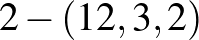A következő lehetséges (az oszthatósági feltételeket teljesítő) paraméterhármasok: $2-(9,3,2)$ , $2-(10,3,2)$ és $2-(12,3,2)$ . Mindhárom esetben adhatók a fentiekhez hasonló elemi konstrukciók, melyek közül az elsőre hamarosan visszatérünk, a másodikra is mutatunk példát, a harmadikat pedig „házi feladatként” az olvasóra hagyjuk.

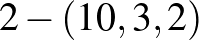$2-(10,3,2)$ :

Legyen 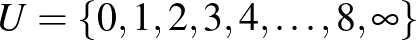$U=\{0,1,2,3,4,\dots,8,\infty\}$ , a blokkok (összesen 30) pedig négyfélék:

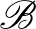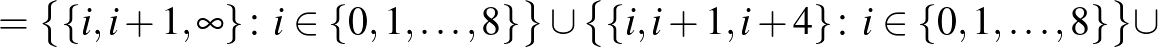$\displaystyle \mathcal{B}$	$\displaystyle =\bigl\{\{i,i+1,\infty\}\colon i \in \{0,1,\dots,8\}\bigr\}\cup \bigl\{\{i,i+1,i+4\}\colon i \in \{0,1,\dots,8\}\bigr\}\cup$
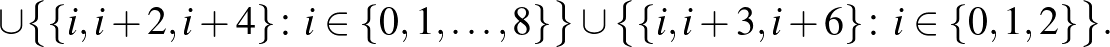	$\displaystyle \qquad \cup \bigl\{\{i,i+2,i+4\}\colon i \in \{0,1,\dots,8\}\bigr\}\cup \bigl\{\{i,i+3,i+6\}\colon i \in \{0,1,2\}\bigr\}.$

A konstrukcióban az összeadást mod 9 értjük. Ha a 2 kiválasztott elem közül egyik a 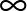$\infty$ , akkor az első típusú blokkból van mindkettő olyan blokk, ami tartalmazza ezt a két elemet. Ha mindkét kiválasztott elem a 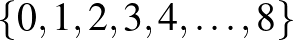$\{0,1,2,3,4,\dots,8\}$ -ból való, akkor a mod 9 „távolságuk” alapján esetekre bontva a lehetőségeket, mindig 2 megfelelő blokkot találunk.

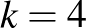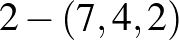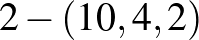Nézzük a $k=4$ esetet. Az oszthatósági feltételek szerint a legkisebb lehetséges, nemtriviális megoldások a $2-(7,4,2)$ és $2-(10,4,2)$ blokkrendszerek.

Az elsőre egyszerű konstrukció adható úgy, hogy a Fano-sík ponthalmazán blokkoknak tekintjük az egyenesek komplementereit (amik épp a sík 4-ívei, ún. hiperoválisok):

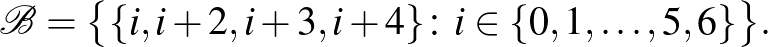
$\displaystyle \mathcal{B}=\bigl\{\{i,i+2,i+3,i+4\}\colon i \in \{0,1,\dots,5,6\}\bigr\}.$

A konstrukcióban az összeadást itt is mod 7 értjük. A kapott blokkrendszer pedig példa bisíkra (olyan 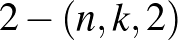$2-(n,k,2)$ blokkrendszerre, ahol a blokkok száma megegyezik az alaphalmaz elemszámával). Egy 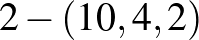$2-(10,4,2)$ blokkrendszer megadását házi feladatként az olvasóra hagyjuk.

Tekintsük a 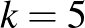$k=5$ esetet. Ekkor a legkisebb paraméterhármas, ami teljesíti az oszthatósági feltételeket, a 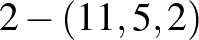$2-(11,5,2)$ . Ebben az esetben Paley nevéhez fűződő (szintén bisíkot adó) konstrukciót mutatunk.

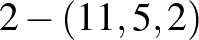$2-(11,5,2)$ :

Legyen 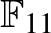$\mathbb{F}_{11}$ a 11-elemű test (a testben mod 11 definiáljuk az összeadást és a szorzást is). Az 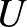$U$ alaphalmaz elemei pedig legyenek ennek a testnek az elemei, 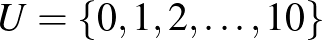$U=\{0,1,2,\dots,10\}$ . A blokkok a test nemnulla négyzetelemeinek (azaz olyan testelemeinek, amelyek előállnak valamelyik testelem négyzeteként) halmazát, a 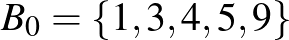${B}_0=\{1,3,4,5,9\}$ blokkot „eltolva” adódó 5-elemű részhalmazok:

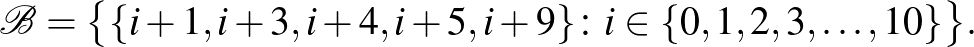
$\displaystyle \mathcal{B}=\bigl\{\{i+1,i+3,i+4,i+5,i+9\}\colon i \in \{0,1,2,3,\dots,10\}\bigr\}.$

A kapott halmazrendszer valóban 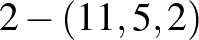$2-(11,5,2)$ blokkrendszer (és mivel a blokkok száma épp 11, így bisík is), ami azon múlik, hogy minden blokkban teljesül, hogy a blokk elemeiből képezhető különbségek a test minden (nemnulla) elemét pontosan kétszer állítják elő. Megjegyezzük, hogy a test nemnulla nem-négyzetelemeinek halmazára (és annak eltoltjaira) ugyanez igaz. Ez a tulajdonság később még hasznos lesz egy 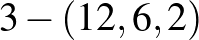$3-(12,6,2)$ blokkrendszer megadásához.

A 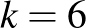$k=6$ esetben a legkisebb lehetséges paraméterhármas a 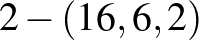$2-(16,6,2)$ , mely esetben bizonyítható, hogy 3 lényegesen különböző ún. Menon-blokkrendszer létezik (ezek is bisíkok). Ezek közül az egyik Kummer nevéhez fűződik, ezt mutatjuk be a következőkben.

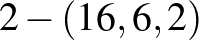$2-(16,6,2)$ :

Legyen 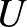$U$ alaphalmaz egy 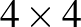$4\times4$ -es rács pontjainak halmaza:

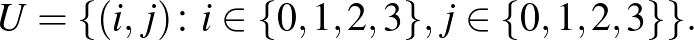
$\displaystyle U=\{(i,j)\colon i\in \{0,1,2,3\}, j\in \{0,1,2,3\} \}.$

A blokkok (összesen 16) pedig legyenek a rács pontjaival indexelve, 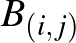$B_{(i,j)}$ tartalmazza az 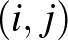$(i,j)$ rácsponttal azonos sorban, illetve azonos oszlopban levő 3-3 rácspontot (az 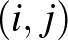$(i,j)$ rácspontot kihagyjuk). A kapott 16 blokk megfelel, minden rácspont pár esetén pontosan 2 mindkettőt tartalmazó blokk van: Ha a két rácspont azonos sorban vagy azonos oszlopban van, akkor a két őket tartalmazó blokk az a sorukban (vagy oszlopukban) levő másik két rácsponttal indexelt blokk. 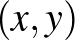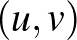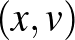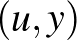Amennyiben a két kiválasztott rácspont $(x,y)$ és $(u,v)$ nincsenek azonos sorban sem oszlopban, akkor pedig a két őket tartalmazó blokk az $(x,v)$ és $(u,y)$ rácspontokkal indexelt blokkok.

A 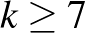$k \geq 7$ esetről bővebben a [2]-ből tájékozódhatnak az érdeklődő olvasók.

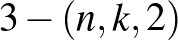blokkrendszerek

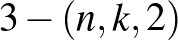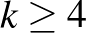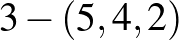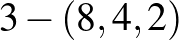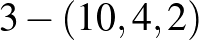A továbbiakban a $3-(n,k,2)$ blokkrendszereket vizsgáljuk. Természetesen a $k \geq 4$ feltétel szükséges. Ebben az esetben a legkisebb, az oszthatósági feltételeket teljesítő paraméterhármasok: $3-(5,4,2)$ , $3-(8,4,2)$ és $3-(10,4,2)$ .

Az első esetben egy 5-elemű alaphalmaz minden 4-elemű részhalmazát tekintve blokkoknak, nyilván 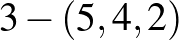$3-(5,4,2)$ blokkrendszert kapunk.

A második esetben, illetve később többször hasznos lesz az alábbi tétel.

2. tétel. (Derivált blokkrendszerek) Ha létezik 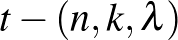$t-(n,k,\lambda)$ blokkrendszer ( 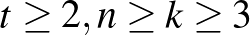$t\geq 2, n\geq k\geq 3$ ), akkor létezik 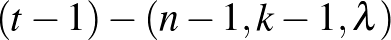$(t-1)-(n-1,k-1,\lambda)$ blokkrendszer.

A bizonyítás egyszerű, ugyanis rögzítve egy 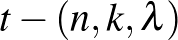$t-(n,k,\lambda)$ blokkrendszer alaphalmazának egy 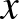$x$ elemét, és blokkoknak tekintve az alaphalmaz azon részhalmazait, amik az 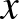$x$ -et tartalmazó eredeti blokkokból adódnak 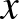$x$ törlésével, a kapott ún. derivált blokkrendszer paraméterei 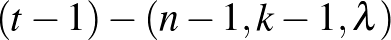$(t-1)-(n-1,k-1,\lambda)$ . Gondoljuk meg, hogy ugyanezt a deriválási eljárást hajtottuk végre, abban a speciális esetben is, amikor prímhatvány 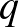$q$ esetén egy sztereografikus projekcióval kaptuk a 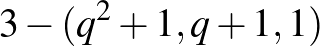$3-(q^2+1,q+1,1)$ Möbius-síkból a 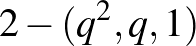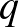$2-(q^2,q,1)$ , $q$ -rendű affin síkot (részletesen lásd [4], 10.33. Lemma). Megjegyezzük, hogy különböző alaphalmazbeli 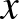$x$ elemekhez nem feltétlenül tartoznak egymással izomorf derivált blokkrendszerek.

A nehezebb kérdés az, hogy az eljárás mikor fordítható meg, azaz egy 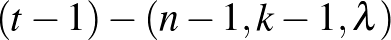$(t-1)-(n-1,k-1,\lambda)$ blokkrendszerből, kibővítve azt, kaphatunk-e 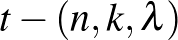$t-(n,k,\lambda)$ blokkrendszert? A válasz általában az, hogy a bővítés nem megoldható, de vannak esetek amikor ez kivitelezhető. Ilyen bővítésekre mutatunk az alábbiakban két példát.

Egy 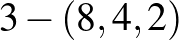$3-(8,4,2)$ blokkrendszer kapható a fentebb konstruált 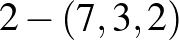$2-(7,3,2)$ blokkrendszer kibővítésével:

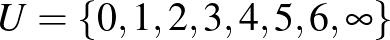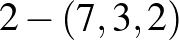Legyen az alaphalmaz $U=\{0,1,2,3,4,5,6,\infty\}$ . A $2-(7,3,2)$ blokkjait kiegészítjük a 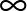$\infty$ elemmel, így kapunk 14 új blokkot. Ugyanezen blokkok 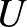$U$ -ra vonatkozó komplementereit is vegyük be a blokkok közé.

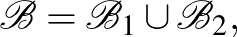
$\displaystyle \mathcal{B}=\mathcal{B}_1 \cup \mathcal{B}_2,$

ahol

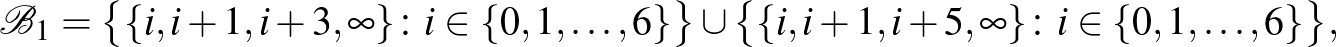$\displaystyle \mathcal{B}_1=\bigl\{\{i,i+1,i+3,\infty\}\colon i \in \{0,1,\dots,6\}\bigr\}\cup \bigl\{\{i,i+1,i+5,\infty\}\colon i \in \{0,1,\dots,6\}\bigr\},$

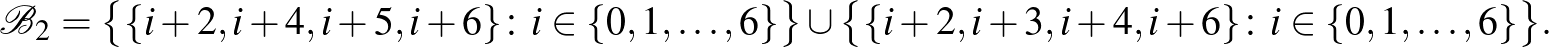$\displaystyle \mathcal{B}_2=\bigl\{\{i+2,i+4,i+5,i+6\}\colon i \in \{0,1,\dots,6\}\bigr\}\cup \bigl\{\{i+2,i+3,i+4,i+6\}\colon i \in \{0,1,\dots,6\}\bigr\}.$

Ez az összesen 28 blokk egy 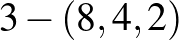$3-(8,4,2)$ blokkrendszert alkot, az ellenőrzés könnyű esetszétválasztás, részletes végiggondolását az olvasóra hagyjuk.

Teljesen hasonló módon kaphatjuk meg a 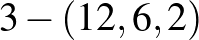$3-(12,6,2)$ blokkrendszert a korábban konstruált 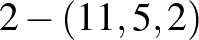$2-(11,5,2)$ Paley-blokkrendszer kibővítésével:

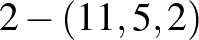Legyen az alaphalmaz $U=\{0,1,2,3,4,5,6,7,8,9,10,\infty\}$ . A fenti $2-(11,5,2)$ blokkjait kiegészítjük a 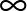$\infty$ elemmel, így kapunk 11 új blokkot. Ugyanezen blokkok 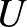$U$ -ra vonatkozó komplementereit is vegyük be a blokkok közé.

Ez az összesen 22 blokk egy 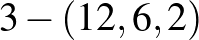$3-(12,6,2)$ blokkrendszert alkot, az ellenőrzés itt is könnyű esetszétválasztás, részletes végiggondolását az olvasóra hagyjuk. (Megjegyezzük, hogy a kapott blokkrendszer egy ún. Hadamard 3-blokkrendszer).

A 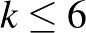$k\leq 6$ esetben 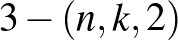$3-(n,k,2)$ blokkrendszerek csak egyetlen eddig nem tárgyalt esetben ismertek (érdemes megjegyezni, hogy a 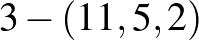$3-(11,5,2)$ paraméterek ugyan teljesítik az oszthatósági feltételeket, mégsem létezik ilyen blokkrendszer). Ez a hiányzó blokkrendszer a 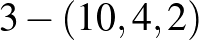$3-(10,4,2)$ paraméterű blokkrendszer, egy ilyet konstruálunk az alábbiakban.

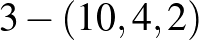$3-(10,4,2)$ :

Legyen az alaphalmaz:

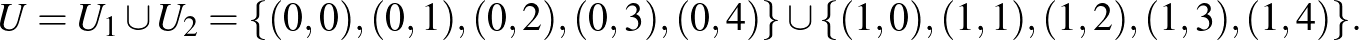
$\displaystyle U=U_1\cup U_2=\{(0,0),(0,1),(0,2),(0,3),(0,4)\}\cup\{(1,0),(1,1),(1,2),(1,3),(1,4)\}.$

A blokkok pedig:

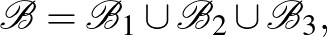
$\displaystyle \mathcal{B}=\mathcal{B}_1\cup \mathcal{B}_2\cup \mathcal{B}_3,$

ahol:

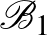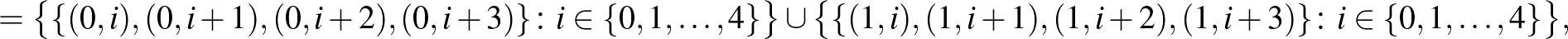$\displaystyle \mathcal{B}_1$	$\displaystyle =\bigl\{\{(0,i),(0,i+1),(0,i+2),(0,i+3)\}\colon i\in \{0,1,\dots,... ...\cup\bigl\{\{(1,i),(1,i+1),(1,i+2),(1,i+3)\}\colon i\in \{0,1,\dots,4\}\bigr\},$
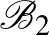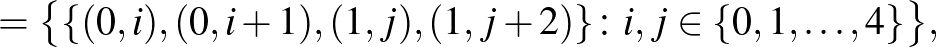$\displaystyle \mathcal{B}_2$	$\displaystyle =\bigl\{\{(0,i),(0,i+1),(1,j),(1,j+2)\}\colon i,j\in \{0,1,\dots,4\}\bigr\},$
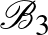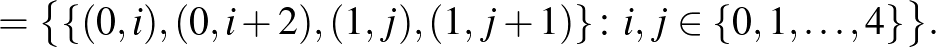$\displaystyle \mathcal{B}_3$	$\displaystyle =\bigl\{\{(0,i),(0,i+2),(1,j),(1,j+1)\}\colon i,j\in \{0,1,\dots,4\}\bigr\}.$

Az alaphalmazbeli elemek második koordinátáiban a számítások mod 5 értendők. Könnyen ellenőrizhető, hogy az így adódó 60 részhalmaz 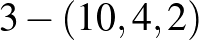$3-(10,4,2)$ blokkrendszert alkot. Amennyiben a 3 kiválasztott alaphalmazbeli elem mindegyike 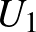$U_1$ -ből vagy mindegyik 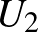$U_2$ -ből való, akkor az őket tartalmazó mindkét blokk 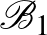$\mathcal{B}_1$ -beli. Ha a kiválasztott 3 elem közül kettő 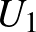$U_1$ -ből, egy pedig 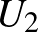$U_2$ -ből származik, vagy fordítva, akkor az őket tartalmazó két blokk 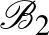$\mathcal{B}_2$ -ből és 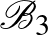$\mathcal{B}_3$ -ból származik.

Ebből a blokkrendszerből a fenti módon (egy alaphalmazbeli elemet rögzítve) kaphatjuk a korábban már említett 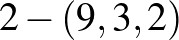$2-(9,3,2)$ derivált blokkrendszert.

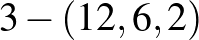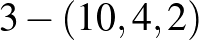Az utolsó két 3-blokkrendszerünkből ( $3-(12,6,2)$ és $3-(10,4,2)$ ) egy 12 és egy 10 lapos „Møbee Twin” pakli gyártható, laponként 11, illetve 24 figurával, ahol bármely három lapon pontosan 2 közös figura található és a paklikban összesen rendre 22, illetve 60 figura fordul elő.

Hivatkozások

: [1] Hajnal Péter: Halmazrendszerek, Polygon Kiadó, Szeged 2002.
: [2] P. Kaski, P. R. J. Östergård: Classification algorithms for codes and designs, Springer 2006.
: [3] Kárteszi Ferenc: Bevezetés a véges geometriákba, Akadémiai Kiadó, Budapest, 1973.
: [4] Kiss György, Szőnyi Tamás: Véges geometriák, Polygon Kiadó, Szeged, 2001.
: [5] Ruff János: Möbius-síkok, blokkrendszerek, Møbee játék, Érintő 2024. március.