Kollár János, a modulusterek varázslója

Kollár János munkássága a matematika sok ágára terjed ki. Itt ezek közül a legjelentősebb területre, az algebrai geometriára, és azon belül is a magasabb dimenziós algebrai geometriára koncentrálunk.

Mi is az az algebrai geometria? Első közelítésben a matematikának ez az ága azzal foglalkozik, hogy algebrai módszerekkel keressen választ geometriai kérdésekre, bár aki kihatóbban foglalkozik a témával hamar ráébred, hogy a kapcsolat sokkal bonyolultabb és inkább arról van szó, hogy az algebra és a geometria valójában ugyanannak a problémának a két látszólag különböző megközelítése. Mindkét oldal részt vesz a problémák megoldásában is és az alkalmazásokban is.

A XVII-ik században Fermat és Descartes bevezették a koordináta-rendszert, amelyet az algebrai geometria kezdetének tekinthetünk. A koordináta-rendszer arra ad lehetőséget, hogy egy geometriai kérdést lefordítsunk az algebra nyelvére. Hasonlóan, fordítva is gondolkodhatunk, és tekinthetünk algebrailag definiált halmazokat. Ilyen például a kör vagy a gömb, amelyeket az , illetve az 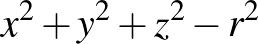polinomokkal tudunk definiálni. Hasonlóak a kúpszeletek, az ellipszis, a hiperbola, a parabola és sok más jól ismert geometriai alakzat.

A polinomok megoldásait kutatva hamar eljutunk a komplex számokhoz, vagy általánosabban az algebrailag zárt testekhez. Az egyszerűség kedvéért a komplex számokra fogunk szoriíkozni. Más szavakkal, a továbbiakban feltesszük, hogy a polinomok és megoldásaik a komplex számtest, azaz felett lesznek definiálva.

A kört, vagy általánosabban egy síkgörbét tekinthetünk úgy, mint egy kétváltozós polinom megoldáshalmazát: Ha 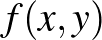egy polinom, akkor tekintsük a

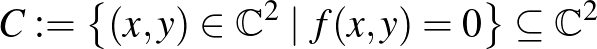
halmazt. Habár ezt a halmazt síkgörbének, vagy általánosabban algebrai görbének nevezzük, a szokásos dimenziófogalmunk értelmében ezek felületnek tűnnek. Ez a látszólagos ellentmondás abból adódik, hogy a komplex számok halmazát, úgymond a komplex „számegyenest" egy síkkal reprezentáljuk, és ezért ami a komplex számok felett egydimenziós, az topológiailag, vagyis úgymond „ránézésre”, kétdimenziósnak látszik. Ez az oka, hogy az algebrai görbéket – a felfedezőjükről, Bernhard Riemannról elnevezve – Riemann-felületekként is ismerjük.

A Riemann-felületek elmélete rendkívül kiterjedt. A történetük és a jelenleg még mindig aktív kutatásuk sok nem algebrai módszert is használ, de ezen belül az algebrai elmélet is sokrétű és szerteágazó. Nem sokat veszítünk az általánosságból, ha kompakt Riemann-felületekre szorítkozunk, ezért mostantól kezdve csak ezekkel fogunk foglalkozni.

A (kompakt, komplex) Riemann-felületek osztályozása egyszerűen indul: topológiai szempontból egyetlen paraméter számít, a nemszám, vagy génusz, amit 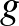-vel jelölünk. Ez az érték a felületen levő lyukak száma. A szóban forgó felület Euler-karakterisztikáját a formula adja meg.

Topológiailag ekvivalens Riemann-felületek lehetnek eltérőek algebrai, analitikus vagy differenciálgeometriai szemszögből. Ez a 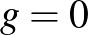esetben még nem jelentkezik, az egyetlen kompakt komplex Riemann-felület a gömb, vagyis a komplex számsík egypontos kompaktifikációja, amit úgy is ismerünk, mint a komplex projektív egyenes. A 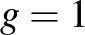esetben, azaz amikor a felület topológiailag egy tórusz, van még egy releváns paraméter, az úgynevezett -invariáns, ami osztályozza az 1 génuszú kompakt komplex Riemann-felületek 1-paraméteres családját.

A 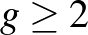génuszú Riemann-felületek egymáshoz hasonlóan viselkednek  (és különbözően, mint a 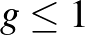génuszúak), ezért gyakran ezeket együtt vizsgáljuk. Ezeket a felületeket általános típusúként is ismerjük. Hamarosan ezeknek a magasabb dimenziós rokonaival fogunk foglalkozni és ezért mostantól kezdve „Riemann-felület” helyett algebrai görbének fogjuk őket hívni.

Tehát az általános típusú algebrai görbék családja magába foglalja az összes algebrai görbét, kivéve azokat, amelyek a gömbbel vagy a tórusszal homeomorfak. Ahogy a génusz nő, egyre több algebrailag nem ekvivalens görbét találunk, és ennek megfelelően a megértésük egyre nehezebbé válik. Már Riemann tudta, hogy a 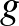génuszú algebrai görbék családját paraméterrel lehet leírni. Ezeket a paramétereket Riemann modulusnak nevezte el. Innen származik a modulustér fogalma, az egy olyan geometriai objektum, amely egy adott osztály tagjainak az izomorfizmusosztályait parametrizálja.

Annak ellenére, hogy Riemann megálmodta ezeket a modulustereket, az aktuális konstrukciójukhoz hosszú út vezetett el, és végül a 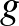génuszú algebrai görbék modulusterét David Mumford konstruálta meg a 1960-as években. Ez önmagában is egy nagyon fontos eredmény, de Mumford még többet is tett. A modulusterek hasznossága abban rejlik, hogy a geometriájuk magában foglalja azt, hogy a kérdéses objektumok – ezeket ezentúl varietásnak fogjuk nevezni – ez esetben az algebrai görbék, milyen családokat alkotnak, vagyis hogyan lehet őket deformálni. Ezen túlmenően, az is egy érdekes kérdés, hogy milyen degenerációjuk van ezeknek a görbéknek. Például, a kúpszeletek osztályozásában a degenerált eseteket, azaz a két metsző egyenest és a dupla egyenest is felsoroljuk. Ennek a moduluselméleti megfelelője az, hogy a kezdeti modulusproblémát kiterjesztjük úgy, hogy az így kapott nagyobb osztálynak a modulustere kompakt legyen, ami azt eredményezi, hogy a degenerációkat is parametrizáljuk. A görbék esetében ez a nagyobb osztály viszonylag egyszerű, de ehhez előbb meg kell említenünk a szingularitásokat, azaz olyan pontokat ahol a görbe nem egy sokaság, vagyis ahol a tangenstér 1-nél nagyobb dimenziós. A kiterjesztett problémában szereplő görbéket stabilnak hívjuk. A stabil görbék lehetnek szingulárisak, de a lehető legegyszerűbb módon, azaz úgy, hogy lokálisan két metsző egyeneshez hasonlítanak. A 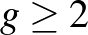feltételt pedig lecseréljük egy azzal ekvivalens feltételre, ami szinguláris varietásokra is értelmezett. Mumford, a Geometriai Invariáns Elmélet (vagy GIT, az angol megfelelőnek a röviditése alapján) segítségével bebizonyította, hogy a stabil görbéknek is létezik modulusterük, ami egy projektív varietás, azaz egy olyan komplex analitikus tér, amely egy komplex projektív térbe beágyazható mint zárt halmaz.

Ezzel lezárult a kérdés a görbék modulustereinek létezéséről, de ezeknek a modulustereknek a vizsgálata a mai napig folyik. Az alkalmazások száma szinte leírhatatlanul nagy, ami természetesen már Mumfordot és sok más követőjét arra vezette, hogy a görbék esetéhez hasonlóan megpróbálják a felületek és a magasabb dimenziós varietások modulustereit is megkonstruálni.

Ez a törekvés valamennyire sikeres volt a sima felületek esetében, de már a stabil felületek definíciója is eleinte túl nehéznek bizonyult. A korrekt definíciót Kollár János és Nicholas Shepherd-Barron adta meg 1988-ban [6]. Azonban a stabil, illetve ahogyan most ismeretes, a KSB-stabil felületek modulusterének létezésere újabb három évtizedet kellett várni. Az a jó hír, hogy ezek létezését sikerült egyszerre bizonyítani az összes dimenzióban. Ez valószínűleg azért történt így, mert utólag kiderült, hogy a felületek elmélete már minden problémát és akadályt bemutat [4].

A fennt említett modulusterek megkonstruálása a központi témája Kollár János 2023-ban megjelent Families of varieties of general type című könyvének [3]. Ez a könyv messzemenőkig eltér a szokásostól. A könyv nagyrésze eddig nem publikált eredményeket tartalmaz, és több új fogalom is szerepel benne, amelyek szükségesek voltak az elmélet teljessé tételéhez.

Miért is volt ez a probléma annyira nehéz? Az első akadály az volt, hogy bár a GIT nagyon hasznos módszer a görbék es a vektornyalábok tanulmányozásához, a magasabb dimenziós varietásokhoz nem bizonyult megfelelőnek, és ezért más módszerekre volt szükség.

A varietások egy adott osztálya modulusterének a konstruálásához az első szükséges lépés az, hogy valahogyan összegyűjtsük ezeket a varietásokat egy helyre. A megvalósítás ötlete Teruhisa Matsusakától, Kollár János doktori témavezetőjétől, származik. Matsusaka azt javasolta, hogy a kérdéses varietásokat egy adott projektív térbe kell beágyazni. Ezzel azt érjük el, hogy az összes varietás, amelyet parametrizálni szeretnénk, egy fix térnek a részvarietása és így ennek az adott térnek a geometriáját használhatjuk arra, hogy a kérdéses varietásokról többet megtudjunk.

Matsusaka 1972-ben bebizonyította, hogy ez a beágyazás valóban lehetséges. Ez az eredmény úgy ismeretes, mint Matsusaka Nagy Tétele (Matsusaka's Big Theorem).

Sajnos akkor ez az eredmény még csak sima varietásokra volt ismert, de akkor még a KSB-stabil varietások definíciója sem volt definiálva, úgyhogy ez teljesen érthető. A megfelelő tételt KSB-stabil varietásokra Christopher Hacon, James McKernan és Chenyang Xu bizonyította 2018-ban.

Ettől az eredménytől függetlenül a felületek és magasabb dimenziós varietások modulustér-elmélete egy alapvető problémába ütközik az első lépésnél, ami teljesen megváltoztatja a helyzetet a görbékhez képest. A Matsusaka által kijelölt célt úgy lehet elérni, hogy egy megfelelő egyenesnyalábot választunk az összes szóban forgó varietáson egyszerre. Ezt az egyenesnyalábot a görbék esetében a differenciálformák nyalábja adja. Eredetileg ezt sima varietásokra értelmezzük, de a sima definíciót ki lehet terjeszteni enyhén szinguláris varietásokra, például a KSB-stabil varietásokra is. A probléma abból ered, hogy a görbék esetében a stabil görbékre egy egyenes nyalábot kapunk, de már a felületek esetében is a megfelelő kiterjesztés csak egy úgynevezett 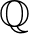-egyenes nyaláb, azaz egy olyan kéve, ami önmaga nem feltétlenül egyenes nyaláb, de amelynek egy megfelelő hatványa egy egyenes nyaláb. Ezt a hatványt fel lehet használni, hogy a Matsusaka-féle beágyazást megkapjuk, de ez újabb nehézséget okoz: a  moduluselmélet azt kívánja, hogy az összes varietásra ugyanazt a hatványt használjuk. Ez azt eredményezi, hogy egy-egy adott deformációt tekintve nehéz megállapítani, hogy mi az a hatvány, ami az összes többi varietásra is működik. Ezt a problémát Kollár ismerte fel több mint 30 évvel ezelőtt, de a megoldásra 2013-ig kellett várni. Talán nem meglepő módon a megoldás is Kollártól származik. Ez a probléma kulcsfontosságú volt a magasabb dimenziós varietások elméletében, és amíg meg nem született a megoldása, nem sok előrelépés történt.

Ez a motívum végigkísérte a modulusterek elméletét az elmúlt 30 évben: felmerül egy akadály, amire találunk egy megoldást, de a megoldás rövidesen egy újabb akadályhoz vezet. Az akadályok és megoldásaik fokozódóan nehezebbé válnak. Ezen akadályok oroszlánrészét Kollár oldotta meg és a megoldások nagy része a Families of varieties of general type-ban került először publikálásra.

Az egyik ilyen probléma és annak a megoldása áll a vadonatúj -laposság fogalma mögött. Ez is Kollár egyik jelentős felfedezése. A laposság egy régóta ismert és használt fogalom, ami a modulusterek elméletében alapvető szerepet játszik. Azonban a fent említett akadályok egyike az, hogy bizonyos segédobjektumokra, amelyek a varietásainkon élnek és fontos szerepet játszanak a modulusfeladat leírásában, nem követelhetjük meg, hogy laposak legyenek. Ugyanakkor valamilyen megszorításra mindenképpen szükség van, és azt szeretnénk, hogy ezek annyira laposak legyenek, amennyire csak lehetséges. Más szóval egy új fogalomra van szükség, ami a laposságnál egy kicsit gyengébb, de továbbra is elég erős ahhoz, hogy alkalmazható legyen. Ezt az elvárást tölti be a -laposság. Érdekes módon, bár általában a laposságnál ez egy gyengébb fogalom, bizonyos helyzetekben jobban viselkedik annál.

Ahogyan említettük, ez a könyv inkább egy 500 oldalas tudományos dolgozat, egy 3 évtizedes tudományos program eredménye. Jelenleg ez az egyetlen forrás, ahol a magasabb dimenziós varietások moduluselméletének eredményeit el lehet érni. Megjelenése óta szinte azonnal alapvető tankönyvvé és elengedhetetlen kutatási forrásanyaggá vált.

Egy ilyen könyv megírása önmagában is hatalmas fegyvertény, de ez Kollár munkásságának csak egy részét mutatja be. Mindenekelőtt meg kell említeni, hogy ennek a könyvnek van egy „előzetese”. A Singularities of the minimal model program [2] eredetileg a bevezető fejezete lett volna a modulustérről szóló könyvnek, de hamarosan kinőtte magát egy teljes könyvvé. Ez a tény önmagában bepillantást ad arra, hogy ez a téma mennyire összetett, nehéz és szerteágazó.

Kollár eredményei számosak és sokrétűek. Eltűnési tételektől kezdve projektivitási kérdéseken keresztül, kitérnek az algebrai varietások topológiai és differenciálgeometriai tulajdonságaira. Mori mellett, ő a minimális model program egyik főépítésze. Az 1998-as könyvük [5] mind a mai napig a legalapvetőbb tankönyv ebben a témában. Kollár volt az egyik legfőbb úttörője a varietásokon található racionális görbék tanulmányozásának és annak, hogy ezek hogyan és milyen mértékben befolyásolják a kérdéses varietás geometriáját. Ebben a témában írt könyve [1] szintén alapvető fontossággal bír.

Kollár bizonyitásai konceptuálisak és feltárják annak mélyebb okait, hogy egy-egy állítás miért is igaz, ezért az eredményei széles körben alkalmazhatók. Ez a rövid cikk nem alkalmas arra, hogy Kollár teljes munkásságát bemutassa. Csak maguknak a témáknak a felsorolása, amelyekben jelentős eredményeket ért el, szükségessé tenne egy újabb oldalt, ezért ettől most eltekintünk.

A magasabb dimenziós varietások moduluselmélete matematikusok egy egész csoportja szerteágazó munkáinak eredményeként jött létre. Ennek ellenére a szükséges eredmények nagyrésze Kollártól származik. Ő jelölte ki az útirányt három évtizeddel ezelőtt, ő oldotta meg a legtöbb felmerülő problémát, és ő vezette el a kutatást a végső eredményhez.

Hivatkozások

[1] J. KOLLÁR: Rational curves on algebraic varieties, Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge. A Series of Modern Surveys in Mathematics, vol. 32, Springer-Verlag, Berlin, 1996.

[2] J. KOLLÁR: Singularities of the minimal model program, Cambridge Tracts in Mathematics, vol. 200, Cambridge University Press, 2013, with the collaboration of SÁNDOR J. KOVÁCS.

[3] J. KOLLÁR: Families of varieties of general type, Cambridge Tracts in Mathematics, vol. 231, Cambridge University Press, Cambridge, 2023, With the collaboration of Klaus Altmann and Sándor Kovács.

[4] J. KOLLÁR AND S. J. KOVÁCS: KSB stability is automatic in codimension 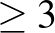, Moduli 1 (2024), Paper No. e5, 19.

[5] J. KOLLÁR AND S. MORI: Birational geometry of algebraic varieties, Cambridge Tracts in Mathematics, vol. 134, Cambridge University Press, Cambridge, 1998, With the collaboration of C. H. Clemens and A. Corti, Translated from the 1998 Japanese original.

[6] J. KOLLÁR AND N. I. SHEPHERD-BARRON: Threefolds and deformations of surface singularities, Invent. Math. 91 (1988), no. 2, 299–338.