A szerda esténkénti előadássorozat különlegessége, hogy utolsó alkalommal a PhD dolgozatomról fogok mesélni. Maga az értekezés nem különlegesebb, mint akármelyik másik disszertáció, nem is aktuálisabb: valójában semmi ok nincs arra, hogy épp ez legyen a téma egy ismeretterjesztő − együttgondolkodós − szórakoztató rendezvénysorozaton. Az indítékom ennek megfelelően eléggé prózai: ha már megírtam, elmesélném az érdeklődőknek, mivel foglalkoztam az elmúlt években. Hiszen érdeklődés az van, már amennyiben a „mondd el miről szól, úgyse fogom érteni” annak számít. Erre a kérdésre eddig is volt kidolgozott válaszom: elmondtam, hogy nemizolált komplex felületszingularitásokról szól, és minden szóról tudok mesélni egy picit. Szoktam rajzolni ilyenkor egy Whitney-esernyőt, annak mindenki örül.
A MateMorfózis nem népszerűsítő előadássorozat abban az értelemben, hogy nem az a cél, hogy a matematika vagy a tudomány népszerű legyen. Sokkal inkább az, hogy bárkinek lehessen köze hozzá. A személy a fontos, nem a tárgy. Így tehát, mondhatni, belefér: nem célom népszerűen beszélni róla, csak minél érthetőbben, és úgy, ahogy számomra izgalmas és érdekes.
Másrészt meg ez nem egy kirakatnak szánt mézesmadzag, ezzel tényleg foglalkoznak a hivatkozáslistámban szereplő szerzők, és én is dolgoztam rajta változó hatékonysággal az elmúlt években. Talán ez önmagában izgalmassá teszi a vállalkozást.
Harmadrészt pedig, bár maga a téma nem népszerű, annál népszerűbb elemekből áll az odavezető út, ráadásul amilyen mákom van, még a címe is felkapott kifejezés mostanában, összemosódva valami homályos képpel az ősrobbanástól Hawkingon át a mesterséges intelligencia uralmáig. Én persze minden alkalmas fórumon - itt is - hangsúlyozni fogom, hogy ezekről nem lesz szó. Bár a fekete lyukakkal távoli rokonságban állnak a mi szingularitásaink és szerkezetileg egészen hasonlatosak az ősrobbanáshoz, amennyiben ezek is egy pontból kinövekedő önmagukba csavarodó 3-dimenziós terek, közvetlen kapcsolatot nem ismerek, és ha van, akkor sem lesz róla szó.
Az első négy alkalom tehát az a bizonyos oda vezető út. A nemizolált komplex felületszingularitások röviden: egy pont körül csavarodó 4-dimenziós terek a 6-dimenziós térben. Legalábbis számomra – kevésbé álmodozó hajlamú matematikusok gondolhatnak rájuk formális algebrai objektumokként is, a modern matematika természetéből fakadóan ezen nem fogunk összeveszni, legfeljebb más irányú intuíciókat nyerni. Az előadássorozat stratégiája tehát: szavanként kibontani az előző meghatározást.
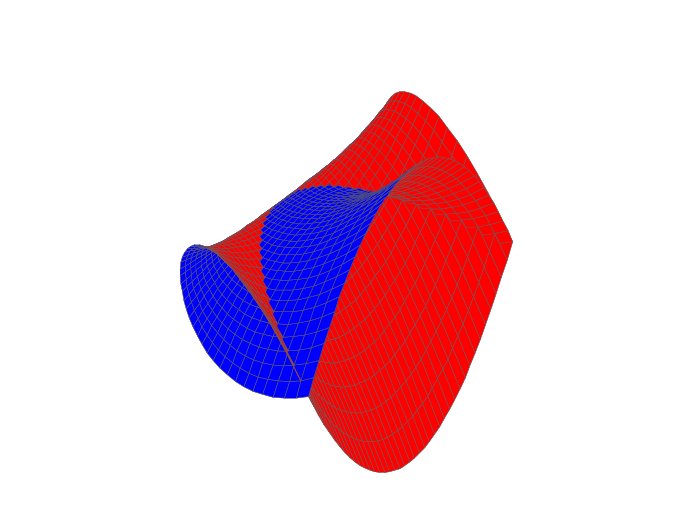
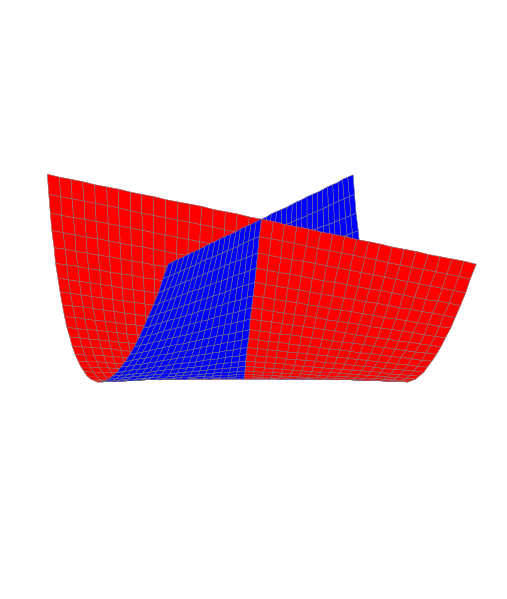
Ápr. 4.: Önmagukba záródó terek − A lyukakat megkerüljük
Első alkalommal megbarátkozunk a csavarodással, a topológia népszerű alakzataival, mint tórusz, Möbiusz-szalag, Klein-kancsó, illetve a lyukasság filozófiailag is érdekes fogalmának geg-szerű megzabolázásával, az úgynevezett fundamentális csoporttal. A honlapon föllelhető Térteremtés ill. Mi a lyuk, hiány vagy tulajdonság c. videókban is ezekről beszélek. Azt hangsúlyozom, ami engem lenyűgözött a témában: hogy egy objektumnak lehet alakja az őt körülvevő tértől függetlenül is, egészen új értelmezést adva ezzel a geometriának. A megközelítés hasonló a Tér alakja című könyvéhez, csak itt távolságokat egyáltalán nem használunk.
Ápr. 11.: Tökéletes ölelés − 4 és több dimenziós gömbök
Magasabb dimenziós terekkel és gömbökkel ismerkedünk, megnézzük, hogyan lehet ilyeneket elképzelni. Szintén nem tartozik a népszerű kategóriába, de kitérek arra is, milyen értelemben léteznek − szerintem − ezek az objektumok, az épp aktuális húrelméleti eredményektől függetlenül. A megálmodott cél két tórusz „tökéletes ölelésben” összeolvadása 3-dimenziós gömbfelületté − ezt a konstrukciót a jin-jang 4-dimenziós, tökéletesített változatának tekintem.
Ápr. 25.: Az akadályokat megkerüljük − komplex számok
Az egész sorozaton végigvonul egy kép különböző formákban: az akadályok kerülgetése, amellyel a fundamentális csoportnál már találkoztunk. Így reményeim szerint ismerős lesz már az algebra alaptételének topológiai szemléltetéséhez. Ezt az igen szemléletes bizonyítást a topológia tanáromtól, Szűcs Andrástól tanultam, megtalálható a jegyzetének első oldalain. MateMorfózis előadásokon nem erőltetem az állítás−bizonyítás szerkezetet, az algebra alaptételét is inkább, mint jelenséget próbálom bemutatni.
Máj. 2.: Katasztrófaelmélet & a gömb kifordítása
„És most jön az ereszkedés...” − ahogy a Bizottság vezette fel a Kalandra fel című lemezének első zeneművét − a lemez nyitányául szolgáló kiabálást követően. Ez történik itt is, a 4. alkalom már a disszertációm alapjául szolgáló fogalmakba vezet be: immerziók, szingularitások. Ez azonban még a népszerű kategória. Megnézzük a gömb kifordításáról szóló 20 perces dialógusos animációt, arról beszélgetünk. Majd a Katasztrófaelmélet népszerű képeiről, a zsenikről és mániákusokról, hullámfrontok szingularitásairól. Semmi mélyebb belemenés, csak ereszkedés.
Máj. 9.: Nemizolált felületszingularitások − MateMorfózis házi védés
Az utolsó alkalmat mindenki saját felelősségére látogathatja. Az értekezésem témája lokális analitikus geometria és topológia keveréke, na ezekről itt − szinte − szó sem lesz. Viszont reményeim szerint az eddig kialakult képekre alapozva be tudom vezetni a leképezések stabilitását intuitívan: ábrákon, animációkon megnézzük, hogyan esik szét egy paraméterezett felület szingularitása Whitney-esernyőkre és háromszoros pontokra, látni fogjuk a peremen megjelenő síkgörbe-immerziót, ami ismerős lesz az előző heti filmből. Innét már el tudom mondani, miről szól az első eredmény a tézisemben: paraméterezett komplex felület szingularitása körül megjelenő immerzió Smale-invariánsa megegyezik a stabilizálás során keletkező Whitney-esernyők számával. A másik eredmény is látszódni fog a valós képen: a Milnor-fibrum pereméhez az immerzió képét kell átműteni. A cél, hogy összekössük ezt a jelenséget a tökéletes öleléssel. Reméljük a legjobbakat.
Mindegyik alkalommal előadás jellegű program lesz 18:30-20:30-ig, aztán szünet után kötetlenebb beszélgetés. A rendezvényre minden érdeklődőt szeretettel várok! Helyszín: Gólya, Bókay utca − Práter utca sarok.
Pintér Gergő
MTA Rényi Alfréd Matematikai Kutatóintézet
