„Földtől eloldja az eget
a hajnal s tiszta, lágy szavára
a bogarak, a gyerekek
kipörögnek a napvilágra;
a levegőben semmi pára,
a csilló könnyűség lebeg!
Az éjjel rászálltak a fákra,
mint kis lepkék, a levelek.”
(József Attila: Eszmélet I.)
1. Személyes motiváció (bevezetés helyett)
I. Majdnem tizenöt évvel ezelőtt hallgattam néhai Rózsa Pál professzor mátrixelmélet kurzusát. Könyvének (Bevezetés a mátrixelméletbe [27]) legelső hivatkozására máig emlékszem, Beke Manó: Determinánsok, 1915 [2]. Fennakadtam rajta, hogy egyrészt komolyan, valaki egy egész könyvet írt csak a determinánsokról, másrészt hogy egy 2000 utáni szakkönyv egy 1915-ösre hivatkozik, azért ez sem mindennapi, harmadrészt, hogy milyen vicces neve van a szerzőnek.
II. Nemrégiben olvastam Tverdota György irodalomtörténész Tizenkét vers című könyvét [36], mely József Attila Eszmélet költeményét vizsgálja. Az Eszmélet láthatóan az egyik legizgalmasabb verse József Attila életművének – és mellesleg az egész 20. századi magyar lírának – abban az értelemben feltétlenül, hogy egy komplett könyvet, két könyvhosszúságú tanulmányt, és számtalan cikket írtak erről az egyetlen versről; a róla szervezett 2012-es konferencia anyagát több mint 500 oldalban adták ki. Volt, aki a marxista világképet látta benne, volt aki a marxista világkép elvetését. Elemezték pszichoanalitikusan, posztmodernként, volt aki nemes egyszerűséggel azt mondta, hogy „vonzóereje, megfejtésének reményétől függetlenül, maga a rejtélyesség” [4]. Talán épp értelmezési lehetőségeinek sokfélesége teszi egyik legtalányosabb versünkké. Tverdota könyvének alapállítása, melyre a címe is utal, hogy az Eszméletet valójában nem egységes költeményként, hanem versciklusként lehet (és célszerű) elemezni. A Tizenkét vers kapcsán a legérdekesebb, hogy bár én minden vagyok, csak irodalmár nem, mégis – miközben egyes részei kimondottan mély irodalmi részletkérdésekbe merülnek – számomra is kifejezetten olvasmányos, végig érdekes, és egyáltalán: tanulságos könyv volt.
III. Közel nincs olyan olvasottságom a szépirodalomban, hogy egyáltalán merjek olyat mondani, hogy ki a „kedvenc” költőm, de tény ami tény, a Tiszta szívvel az egyetlen vers, amit fejből tudok (akárhányat is próbált nekem memoriterként a közoktatás megtanítani). Megmondom őszintén, még a Himnuszt sem biztos, hogy elejétől végéig el tudnám mondani bármikor, de a „Nincsen apám versemet” igen.
2. Kérdésfelvetés
Tverdota a könyvének elején, az Eszmélet keletkezésének releváns életrajzi hátterét bemutatva, tesz egy apró megjegyzést: „Olyanfajta barátság fűzhette össze József Attilát és Pákozdyt, amelyben az utóbbi elismeri társa költő és szellemi felsőbbségét. 1934. évi tavaszi együttlétüknek érdekes dokumentuma az 1934. június 20-án kelt, Beke Manó matematikusnak címzett, el nem küldött levél, amelyben a két barát egy vitatott matematikai kérdésben szeretné döntőbírónak felkérni az ismert szakembert.” [36, 26–27.o.].
Az olvasó most értheti meg, hogy mi szükség volt a hosszú, személyes bevezetőre: így válik azt hiszem azonnal világossá, hogy miért döbbentem meg a fenti sorokat olvasva (valószínűleg sokkal jobban, mint Tverdota könyvének bármely olvasója tette ennél a bekezdésnél).
De vajon mi lehet ez a kérdés? Az előbbiek alapján az is érthető, hogy miért kezdett azonnal nagyon furdalni a kíváncsiság, sajnos azonban Tverdota könyve magát a kérdést nem közli. Szerencsére sikerült utánajárnom: az 1. ábrán József Attila és Pákozdy Ferenc ominózus levelének facsimile oldala látható.

1. ábra. József Attila és Pákozdy Ferenc levele Beke Manónak. Forrás: Petőfi Irodalmi Múzeum Kézirattár, JA. 708.
Noha a levél jól olvasható, a biztonság kedvéért közlöm a szöveghű átiratát is:
Méltóságos Uram!
Egy társaságban a következő kérdés merült föl:
Lehetséges-e, hogy a „cikloist” író pont pályája egybeessék a talppontot a tetőponttal összekötő dislokációs egyenessel, ha a gördülési pályát csak a saját – pozitiv vagy negativ – irányába mozgatjuk el? (Félreértés elkerülése végett megjegyezzük, hogy „gördülési pálya” alatt Méltóságod „Bevezetés a differenciál- és integrálszámításba” c. könyvének (Népszerű Főiskola Könyvtára, II. kiad.) 38. oldalán szereplő ábrán 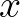 tengelyként jellemzett egyenest értjük.)
tengelyként jellemzett egyenest értjük.)
E lehetőség állitója szerint erre van legalább egy eset, mégpedig akkor, ha a pálya elmozditása a gördüléssel ellenkező irányba történik
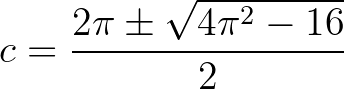 … / sebességgel
… / sebességgel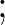
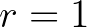 ; gördülési sebesség = 1.
; gördülési sebesség = 1.
Méltóságod szives bocsánatát kérjük a zaklatásért és kérjük, hogy igennel vagy nemmel válaszoljon Méltóságod a mellékelt levelezőlapon.
Megtudta József és Pákozdy a választ erre a kérdésre? Valószínűsíthetően nem, ugyanis az 1976-ban az Akadémiai Kiadónál megjelent József Attila válogatott levelezése című gyűjtemény [6] végjegyzetei között ezt írja a levélről: „A közlés alapjául szolgáló levél nem látszik misszilisnek [tényleges (értsd: nem költői) levélnek – FT]. Nem is fogalmazványjellegű. Írói, valószínűleg, eredeti tervüktől elállottak és nem küldték el a címzettnek.” [6, 466.o.]. A 2006-os, teljesség igényével készült József Attila levelezése hasonlóan nyilatkozik („géppel írott, el nem küldött levél” [12, 407.o.]); érdekesebb az ezt követő megjegyzése a végjegyzetnek: „a […] levelet valószínűleg azért nem küldték el, mert belátták dilettáns voltát” [12, 686.o.]. Sajnos a kötet szerkesztői nem közölték, hogy ez utóbbi megállapításukat mire alapozzák. (Hozzá kell tenni, hogy bár a kérdésre adott válasz tényleg nem különösebben érdekes, de azért dilettánsnak – én legalábbis – nem nevezném.) Péter László József Attila közöttünk című 1980-as könyve szintén megerősíti, hogy a levelet nem küldték el [25, 86.o.].
Mi sem áll távolabb jelen sorok szerzőjétől, mint hogy Beke Manónak képzelje magát, de – noha végeredményben a kérdésfelvetés nem túl izgalmas válaszra vezet, és Józsefék jó eséllyel félreértettek valamit – nem minden tanulság nélküli megválaszolni a feltett kérdést.
3. Eredmény és megbeszélés
3.1. A ciklois fogalma és alkalmazásai
Elöljáróban egy kis magyarázat azok számára, akik nem ismerik a ciklois fogalmát. Képzeljünk el egy vízszintes, egyenes úton gördülő kocsikereket! Képzeletben jelöljük meg az épp földdel érintkező pontját, és nézzük meg, hogy milyen pályát ír le, miközben a kerék tovagördül az úton. Azt látjuk, hogy szép szabályos ívet követ: a földhöz közeledve látszólag lelassul, szinte függőlegesen megy le-föl, a másik oldalon pedig gyorsan suhan vízszintesen. Ezt a görbét hívjuk cikloisnak. A 2. ábra mutatja a cikloist, szemléltetve annak kialakulását is (a https://www.github.com/tamas-ferenci/JozsefAttilaEgyMatematikaiKerdese oldalon mindez animáció formájában is megtekinthető).
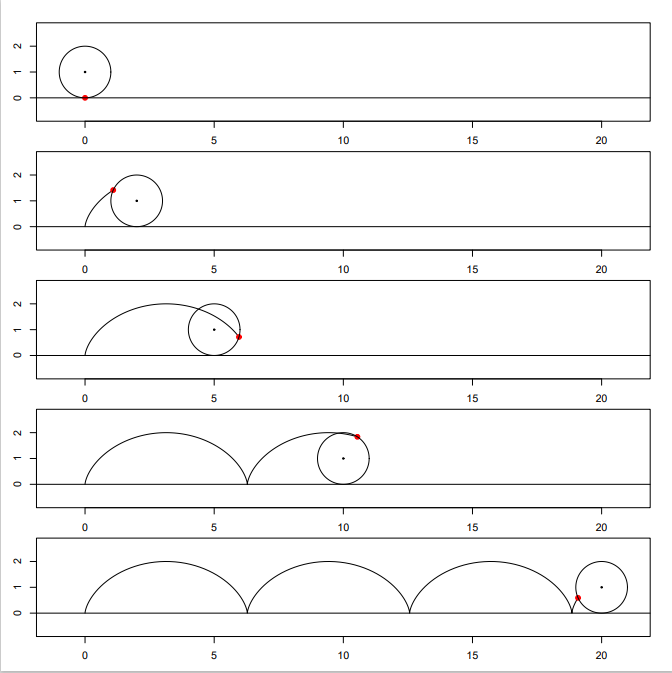
2. ábra. A ciklois görbe és létrejötte.
A ciklois több matematikai probléma kapcsán előjön, ezek közül a két leghíresebbet említem meg itt. Noha a megoldásuk mélyebb eszközöket igényel, maguk a problémák – és az eredmények – teljesen hétköznapi nyelven elmondhatóak (és elég érdekesek is!). A megértés szempontjából nem lényeges, és helyenként matematikailag mélyebb részeket lábjegyzetben közlöm.
3.1.1. A brachisztochron probléma
Az egyik ilyen nevezetes kérdés a brachisztochron probléma: egy függőleges falon kijelölünk két, nem egymás felett lévő pontot. Kiterjedt barkácstudásunk lehetővé teszi, hogy tetszőleges alakú rámpát ácsoljunk a két pont között, amelyen aztán a magasabban fekvő pontból legurítunk egy golyót az alacsonyabban fekvő pontba. Az egyszerűség kedvéért tételezzük fel, hogy a gravitáció mindenhol azonos nagyságú, valamint, hogy a golyó súrlódás nélkül csúszik a rámpán. A kérdés: milyen alakú rámpán fog a legrövidebb idő alatt legurulni a feljebb fekvő pontból a lejjebb fekvő pontba a golyó? Érezhető, hogy az nem lesz jó, ha eleinte szinte vízszintes a rámpa és aztán esik gyorsan, hiszen így nagyon sok idő lesz, míg a gyors esésig „elcsorog” a golyó. Akkor talán pont a fordítottja lesz a jó, eleinte essen meredeken, aztán legyen hosszan vízszintes? Így először nagyon begyorsul, viszont cserében még sokat meg kell tenni egy szinte vízszintes szakaszon. Vagy inkább kössük őket egyszerűen össze egyenesen? Akár az az eretnek gondolat is az eszünkbe juthat, hogy engedjük a golyót a lejjebb fekvő pontnál is mélyebbre, hogy jó nagy lendületet vegyen, és a végén kicsit fordítsuk vissza.
A 3. ábra szemlélteti1, hogy mi lesz a megoldás: a ciklois! Egy ciklois alakú rámpát kell ácsolnunk, és azzal összekötnünk a két pontot, ezen fog a legrövidebb idő alatt eljutni a golyó az egyik pontból a másikba. (Az alábbi és a később következő animációk is megtekinthetők a https://www.github.com/tamas-ferenci/JozsefAttilaEgyMatematikaiKerdese oldalon.)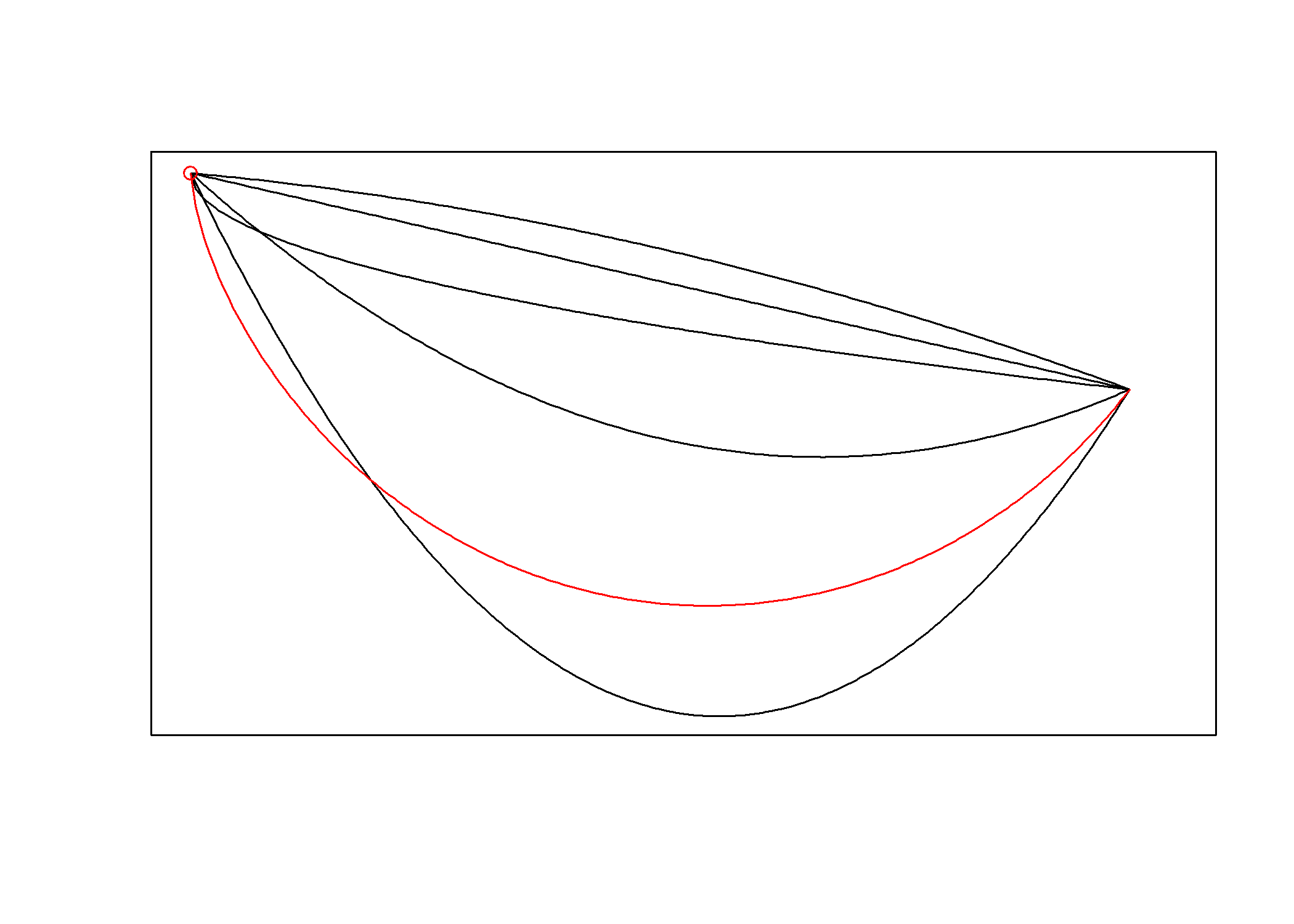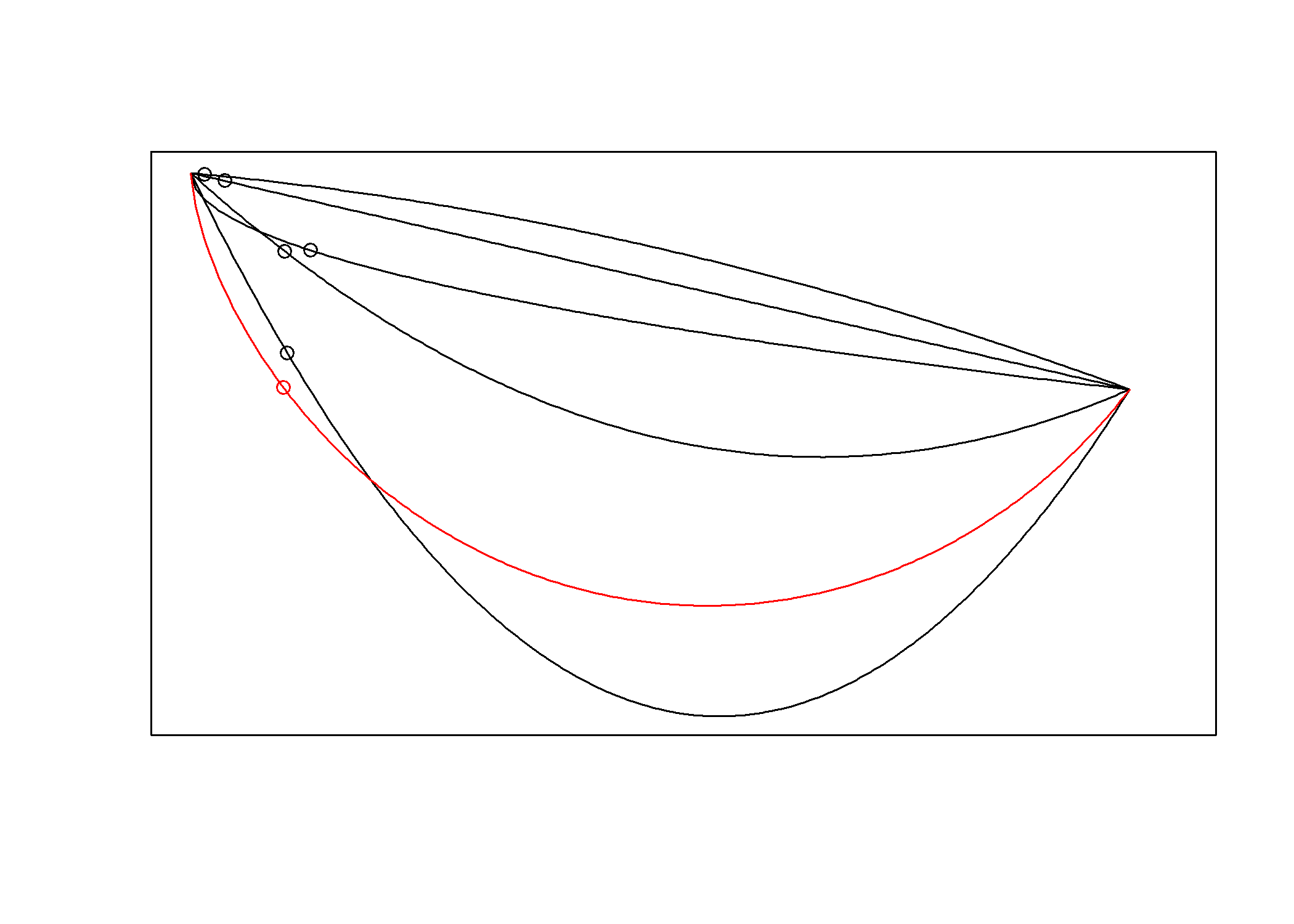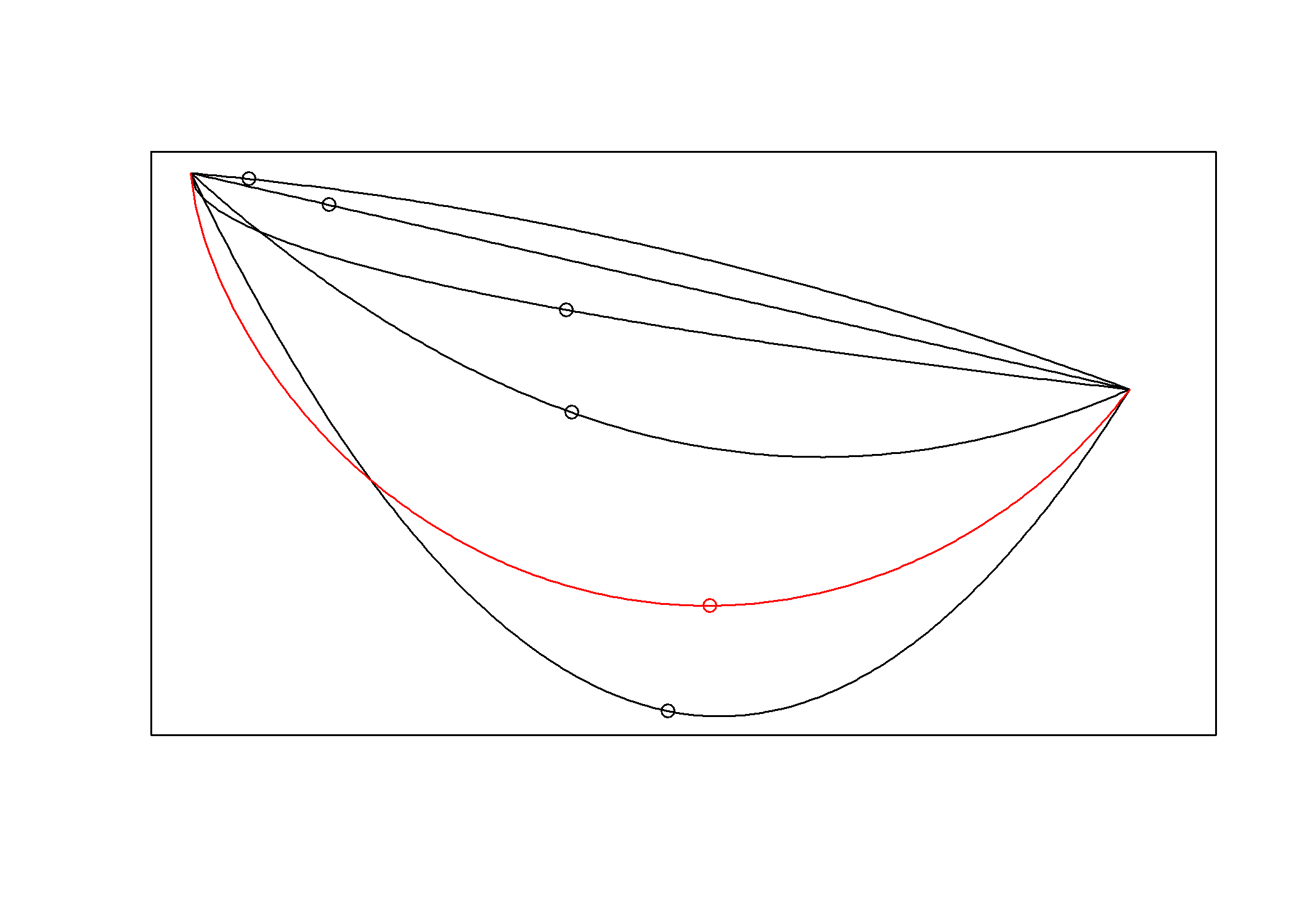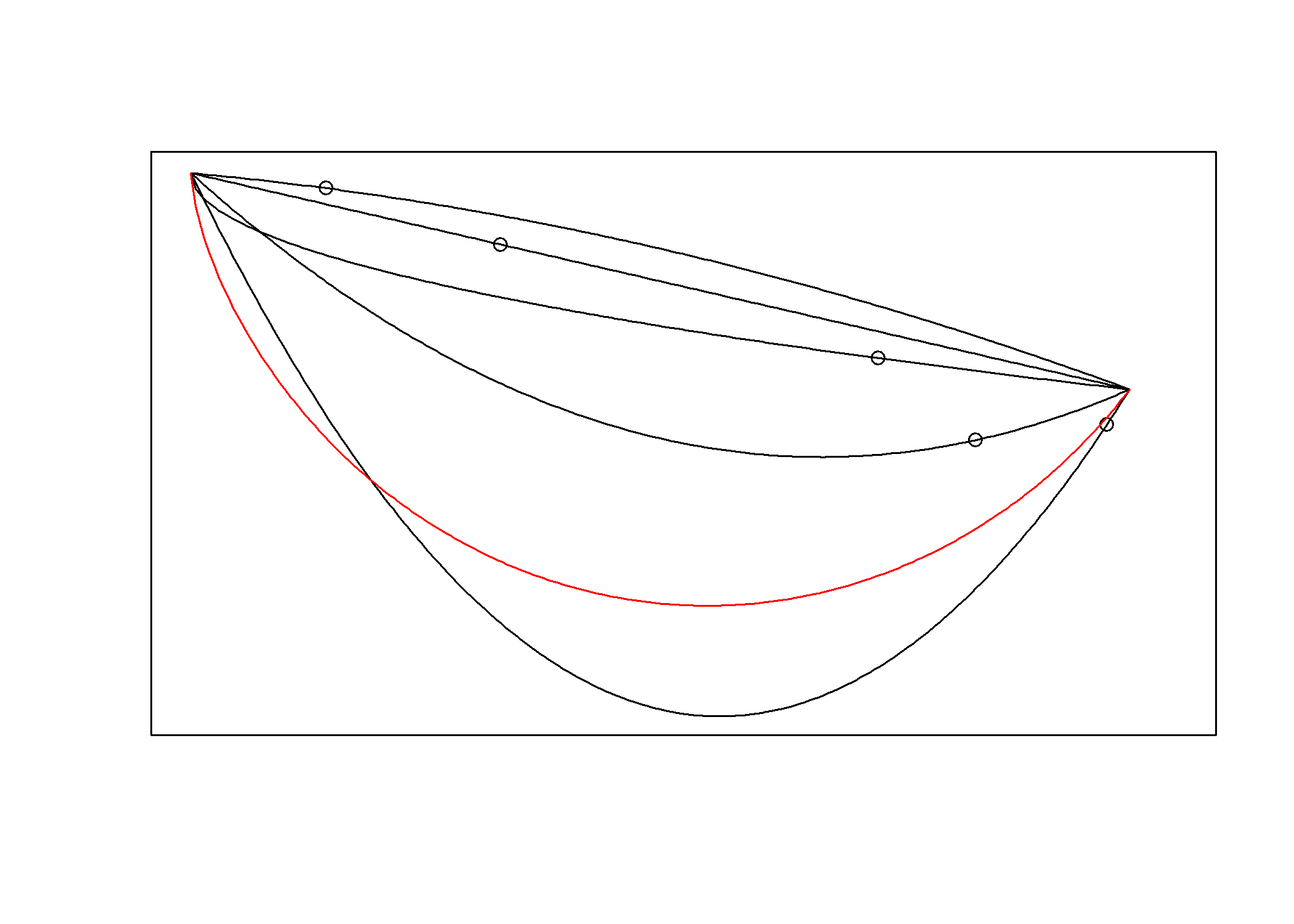
3. ábra. A brachisztochron probléma: a fenti pontból azonos időpontban elindított golyók legurulása különböző alakú pályákon. Az ábra a ciklois mentén (piros görbe) leguruló golyó beérkezése előtti pillanatot ábrázolja; jól látható, hogy a többi golyó többé vagy kevésbé, de mind le van maradva.
A bizonyítás messze meghaladja ezen írás kereteit2, de a történetére egy gondolat erejéig érdemes kitérni. A problémát Johann Bernoulli (a Bernoulli család legelső tudósgenerációjának Johannja) tűzte ki 1696-ban egy folyóiratcikkben, célirányosan a „világ briliáns matematikusait” megszólítva. Valóban elég erős mezőny gyűlt össze: egy évvel később Newton, Leibniz és l'Hospital megoldásait közölte, együtt a sajátjával és a bátyjáéval, Jakob Bernoulliével (aki testvéréhez hasonlóan foglalkozott analízissel, de mellette ő a valószínűségszámítás egyik első nagy alakja). Ők ketten aztán úgy össze is vitatkoztak a megoldásaikon, hogy az éveken át tartó konfliktushoz vezetett [29]. (A Bernoulli famíliában nem teljesen ismeretlen jelenség a családtagok közti irigykedés egymás tudományos eredményeire: az itt is említett Johann kidobta a családi házból a saját fiát, Daniel Bernoullit – az áramlástan későbbi megalapítóját – annyira felhúzta magát azon, hogy megosztva kapták meg a Francia Tudományos Akadémia díját, amit érzése szerint egyedül érdemelt volna meg…)
3.1.2. A tautochron probléma
A másik problémánál is egy függőleges falunk van, rajta két, nem egymás fölött elhelyezkedő ponttal, közöttük ácsolandó rámpával és azon leguruló golyóval, csak itt a kérdés a következő: ácsolható-e olyan rámpa, hogy a golyó mindig ugyanannyi idő alatt ér le rajta az alsó ponthoz, függetlenül attól, hogy honnan indítjuk a rámpa mentén? Tehát akár a tetejéről indítjuk a golyót, akár a közepéről, akár az aljához nagyon közel, mindig ugyanannyi időt vesz igénybe, hogy az alsó ponthoz érjen. (Úgy is megfogalmazhatjuk, hogy ha elindítunk tetszőleges számú golyót a rámpa tetszőleges pontjairól, akkor azok pontosan egy pillanatban érjék utol egymást, mégpedig akkor, amikor mind épp az alsó ponthoz ér.) Megvalósítható ez?
Első ránézésre meglepő, hogy ilyen alakú rámpa egyáltalán létezhet. Sokan ugyanis arra gondolnak, hogy amit feljebbről indítunk, annak nagyobb utat kell megtennie, hogyan érhetné akkor utol egyáltalán a lejjebbről indulót?! Igen ám, de választhatunk olyan alakot, hogy feljebb egyúttal meredekebb is legyen a rámpa, így az onnan induló golyók nagyobb sebességet érjenek el! Tehát a kérdés lényegében az, hogy vajon létezik-e olyan alak, ahol a feljebb lévő nagyobb meredekség pontosan akkora előnyt ad a golyónak, mint amekkora hátrányt a nagyobb út.
A válasz a kérdésre pozitív, és a megfejtés: a ciklois.
Ciklois alakú rámpán ez megvalósul: ha ácsolunk egy kilométer hosszú cikloist és elindítunk egy golyót a végéből, akkor bármilyen nehéz is elhinni, de az pontosan akkor fog az aljára érni, mint az a golyó, amelyet egy arasznyira indítottunk el az aljától. (Természetesen a súrlódástól ennél a feladatnál is eltekintünk.) A 4. ábra ezt szemlélteti, illetve a már említett oldalon is megtalálható az animáció.

4. ábra. A tautochron probléma: a ciklois alakú pálya különböző pontjairól elindított golyók legurulásának néhány „pillanatfelvétele”. Jól látszik, hogy mindegy honnan indult a golyó, ugyanannyi idő kell, hogy leérjen, ezért pontosan az alsó pontban találkoznak, indítási helytől függetlenül.
Említsük meg egy érdekes alkalmazását ennek az eredménynek. Aki középiskolában végigszámolta fizikaórán az inga lengését, talán emlékszik rá, hogy a levezetés úgy indul, hogy „tegyük fel, hogy az ingát csak kicsit térítjük ki”. Néhányan talán arra is emlékeznek, hogy ez azért fontos, hogy a számolásban megjelenő szögfüggvényekre a kis szögeknél működő közelítést3 használni tudjuk. De mi történik, ha a kitérítés nem kicsi? A dolog persze ekkor is végigszámolható, az eredmény sokkal bonyolultabb alakú lesz, de most nekünk nem is ez fontos, hanem az, hogy amit kapunk, az nem csak számértékében fog eltérni a közelítőtől, hanem abban is, hogy a lengés periódusideje – szemben a közelítő számítással – függeni fog a kitérítés mértékétől! A dolog azért érdekes, mert van egy eszköz, ami több mint 200 éven keresztül alapvető fontosságú volt a társadalom és gazdaság működésében, és aminek a pontossága kritikusan függ egy inga periódusidejétől: az ingaóra. Az előzőekből látszik az ingaóra egyik problémája: a periódusidő a valóságban függeni fog attól, hogy mennyire tér ki az ingája, csakhogy ez óhatatlanul változik időben, ami így elkerülhetetlenül hibához vezet.
Christiaan Huygens, aki magát az ingaórát is megvalósította 1656-ban, pár évtizeddel később rájött a megoldásra: olyan ingát kell szerkeszteni, amelynek a súlya egy ciklois alakú pálya mentén leng! Hiszen a tautochron probléma megoldása épp azt mondja, hogy ez esetben a lengés periódusideje nem fog függeni a kitérítéstől. Kérdés persze, hogy hogyan lehet a gyakorlatban elérni, hogy a súly ne egy kör alakú pályán, hanem cikloison lengjen, de Huygens ezt is megoldotta: az inga felfüggesztése köré mindkét oldalra egy – fejjel lefelé fordított – ciklois alakú határolót kell rakni [11]. Miközben az inga leng, a tartó fonala felütközik ezekre a pofákra, és ez az inga súlyát egy ciklois alakú pályára kényszeríti4. Ez az ún. cikloidális inga. A dolog ugyan elméletben valóban megjavította az ingaórát, de a gyakorlatban nem vált be: egyrészt az ingaóra pontatlanságának összes egyéb forrása, pláne a 17. században, lényegesen nagyobb volt, mint a kitéréstől függő periódusidő jelentette hiba (különösen, ha biztosítjuk, hogy a kitérés ne lehessen túl nagy), másrészt a fonál pofára való felütközése mechanikai veszteségekkel jár, úgyhogy a megoldás igazából maga is teremt egy új hibaforrást.
3.2. A ciklois egyenlete
A tárgyalás pontosításához először is vezessünk be egy koordinátarendszert, ami a 2. ábrára ránézve teljesen kézenfekvő lesz: a nyomon követett pont kezdeti pozíciója legyen az origó, a függőleges tengely mutasson függőlegesen, pozitív iránnyal felfelé, a vízszintes pedig vízszintesen, pozitív iránnyal jobbra.
Azért, hogy a kérdést ne bonyolítsuk feleslegesen, a lényegen nem változtató paramétereket válasszuk egységnyire5. Azaz: a kerék sugara legyen 1, a gördülési sebessége pedig olyan, hogy egységnyi idő alatt 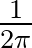 fordulatot tegyen meg a kerék. Ez utóbbi így kimondva egyáltalán nem tűnik egységnyinek, de valójában az, hiszen azt jelenti, hogy
fordulatot tegyen meg a kerék. Ez utóbbi így kimondva egyáltalán nem tűnik egységnyinek, de valójában az, hiszen azt jelenti, hogy 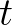 idő alatt
idő alatt 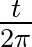 fordulatot tesz meg a kerék, azaz a szögelfordulása épp
fordulatot tesz meg a kerék, azaz a szögelfordulása épp 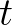 (mivel 1 fordulat az
(mivel 1 fordulat az 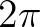 szögelfordulás), ami egyúttal azt is megadja, hogy a középpont épp
szögelfordulás), ami egyúttal azt is megadja, hogy a középpont épp 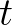 utat haladt jobbra, hiszen az egységnyi kerület miatt
utat haladt jobbra, hiszen az egységnyi kerület miatt 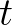 szögelforduláshoz
szögelforduláshoz 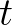 ívhosszúság tartozik, ami „hozzáért” az úthoz, tehát amennyivel odébb ment a kerék6. A szögelfordulást úgy értjük, hogy a kerék középpontját a nyomon követett ponttal összekötő egyenes mennyit fordult el a függőlegeshez képest, a pozitív szög az óramutató járása szerinti elfordulást – jobbra gördülést – jelenti. (A szöget radiánban mérjük.)
ívhosszúság tartozik, ami „hozzáért” az úthoz, tehát amennyivel odébb ment a kerék6. A szögelfordulást úgy értjük, hogy a kerék középpontját a nyomon követett ponttal összekötő egyenes mennyit fordult el a függőlegeshez képest, a pozitív szög az óramutató járása szerinti elfordulást – jobbra gördülést – jelenti. (A szöget radiánban mérjük.)
A ciklois egyenletének az előállítása paraméteres formában egyszerű. Nézzük először a függőleges mozgást! Itt nem számít, hogy a kerék jobbra is gördül, csak annyi a fontos, hogy 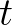 szöget fordult el, ezért a pont
szöget fordult el, ezért a pont 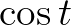 -vel van a középpont alatt (ez persze lehet negatív is – ekkor fölötte van). Mivel a középpont 1-gyel van a talaj fölött, így a pont függőleges koordinátája
-vel van a középpont alatt (ez persze lehet negatív is – ekkor fölötte van). Mivel a középpont 1-gyel van a talaj fölött, így a pont függőleges koordinátája 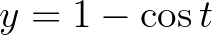 . Vízszintes irányban a középpont
. Vízszintes irányban a középpont 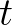 -t haladt jobbra, de a pont
-t haladt jobbra, de a pont 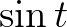 -val van tőle balra (természetesen ez is lehet negatív), így a vízszintes koordinátája
-val van tőle balra (természetesen ez is lehet negatív), így a vízszintes koordinátája 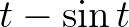 .
.
A ciklois paraméteres egyenletrendszere tehát:
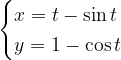
(A matematikai leírás szempontjából nyugodtan el is felejthetjük, hogy a 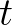 -nek mi idő interpretációt adtunk, a lényeg, hogy a
-nek mi idő interpretációt adtunk, a lényeg, hogy a 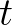 egy nemnegatív valós szám.)
egy nemnegatív valós szám.)
Elő lehet állítani ebből explicit alakot is? Érdekes módon az a válasz, hogy csak az egyik irányban lesz zárt alakú megoldásunk.
Ha ugyanis kifejezzük a 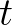 -t
-t 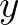 -ból, akkor azt kapjuk, hogy
-ból, akkor azt kapjuk, hogy 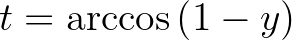 , így
, így
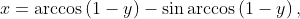
ami egyszerűsítés után
![]()
mivel7 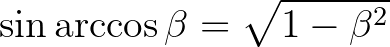 . Természetesen így – szemben a paraméteres alakkal – csak a ciklois egy „ciklusát”, és annak is csak az első felét tudjuk megkapni (logikusan, hiszen utána egy adott
. Természetesen így – szemben a paraméteres alakkal – csak a ciklois egy „ciklusát”, és annak is csak az első felét tudjuk megkapni (logikusan, hiszen utána egy adott 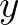 -hoz már több
-hoz már több 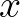 is tartozhat).
is tartozhat).
Ha azonban fordítva akarjuk kifejezni a cikloist, tehát – természetesebb módon – 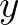 -t az
-t az 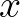 -ből, akkor hamar elakadunk: az
-ből, akkor hamar elakadunk: az 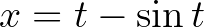 egyenletet kellene megoldanunk
egyenletet kellene megoldanunk 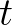 -re, csakhogy ez egy transzcendens egyenlet, aminek nincs zárt alakú megoldása! A cikloist tehát általában nem lehet explicit formában felírni, még egy ciklusra, sőt, még egy fél ciklusra sem.
-re, csakhogy ez egy transzcendens egyenlet, aminek nincs zárt alakú megoldása! A cikloist tehát általában nem lehet explicit formában felírni, még egy ciklusra, sőt, még egy fél ciklusra sem.
3.3. József Attila és Pákozdy Ferenc kérdésének megválaszolása
Térjünk most rá Józsefék kérdésére! Először is állapítsuk meg, hogy a kérdés nem úgy értendő, hogy akkor mi történik, ha a keréknek az úthoz viszonyított sebességét változtatjuk. Tudniillik ha a kereket magát úgy mozgatjuk, hogy egy körbefordulásnyi idő alatt nem egy kerületnyi (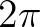 ) utat halad a középpontja, akkor a kerék természetesen kénytelen lesz csúszni. (Pontosabb is lett volna, ha a definícióba belemondjuk, hogy „csúszás nélkül” gördül.) Természetesen az is érdekes matematikai probléma, hogy a csúszásos esetben mi történik, de a kérdés vélhetően nem erre irányult, hiszen úgy fogalmaz, hogy „a gördülési pályát […] mozgatjuk”, tehát a kerék kényszerített mozgatásáról szó sincs. Ettől függetlenül egy gondolat erejéig térjünk ki erre is: ha a kerék csúszik, akkor a leírt pálya vagy hurkolt, vagy nyújtott ciklois lesz [14]. Hogy mik ezek? Rokonai a „szokásos” cikloisnak, olyannyira, hogy megkaphatjuk őket úgy is, hogy csúszásmentesen gördül a kerék, csak épp ekkor nem a kerék kerületén fekvő pontot kell néznünk, hanem egy „küllőjén” találhatót, tehát belső pontot (nyújtott ciklois), vagy a küllő képzeletbeli meghosszabbításában egy külső pontot (hurkolt ciklois). Az 5. ábra mutatja az ilyen görbéket. Ha tehát a kerék csúszását is megengedjük, akkor ilyet fogunk kapni (ha még azt is megengedjük, hogy az ellenkező irányba forogjon mint amerre csúszik, akkor esetleg ezeket tükrözve a vízszintes tengelyre); összefoglaló nevén ezeket a görbéket hívjuk trochoidnak. A dolog még tovább is általánosítható, ha nem egyenes mentén gördítjük a kört, vagy nem kört gördítünk, az így kapott görbéket rulettáknak szokás nevezni [26], de ez már végképp nem tartozik a mostani tárgyunkhoz.
) utat halad a középpontja, akkor a kerék természetesen kénytelen lesz csúszni. (Pontosabb is lett volna, ha a definícióba belemondjuk, hogy „csúszás nélkül” gördül.) Természetesen az is érdekes matematikai probléma, hogy a csúszásos esetben mi történik, de a kérdés vélhetően nem erre irányult, hiszen úgy fogalmaz, hogy „a gördülési pályát […] mozgatjuk”, tehát a kerék kényszerített mozgatásáról szó sincs. Ettől függetlenül egy gondolat erejéig térjünk ki erre is: ha a kerék csúszik, akkor a leírt pálya vagy hurkolt, vagy nyújtott ciklois lesz [14]. Hogy mik ezek? Rokonai a „szokásos” cikloisnak, olyannyira, hogy megkaphatjuk őket úgy is, hogy csúszásmentesen gördül a kerék, csak épp ekkor nem a kerék kerületén fekvő pontot kell néznünk, hanem egy „küllőjén” találhatót, tehát belső pontot (nyújtott ciklois), vagy a küllő képzeletbeli meghosszabbításában egy külső pontot (hurkolt ciklois). Az 5. ábra mutatja az ilyen görbéket. Ha tehát a kerék csúszását is megengedjük, akkor ilyet fogunk kapni (ha még azt is megengedjük, hogy az ellenkező irányba forogjon mint amerre csúszik, akkor esetleg ezeket tükrözve a vízszintes tengelyre); összefoglaló nevén ezeket a görbéket hívjuk trochoidnak. A dolog még tovább is általánosítható, ha nem egyenes mentén gördítjük a kört, vagy nem kört gördítünk, az így kapott görbéket rulettáknak szokás nevezni [26], de ez már végképp nem tartozik a mostani tárgyunkhoz.
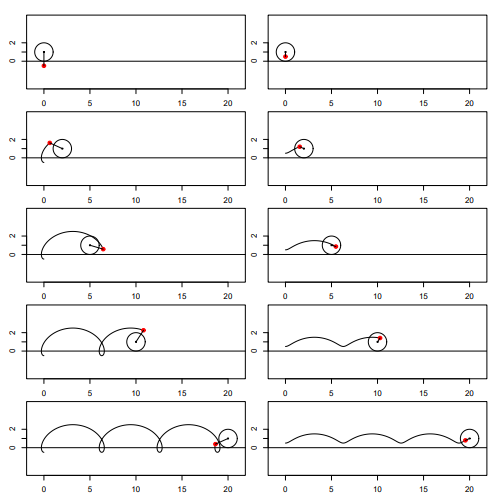
5. ábra. A hurkolt (balra) és a nyújtott (jobbra) ciklois görbék és létrejöttük. Ezeket, együtt a „szokásos” (szép nevén: csúcsos) cikloissal, szokás trochoid görbéknek nevezni. Mozgásban itt lehet látni a hurkolt és a nyújtott cikloist.
De mi a helyzet József Attiláék kérdésével? A megfogalmazás egyértelmű, a pályát magát mozgatjuk, a kerék szép nyugodtan gördül (csúszás nélkül), azt nem befolyásoljuk. Világos, hogy itt nincs a fentihez hasonló csúszási probléma: ha a pályát mozgatjuk (magunkhoz képest), akkor minden sebességnél csúszás nélkül tud haladni a kerék, hiszen annak gördülését a pályához képest értjük. Így már teljesen értelmes a kérdésfelvetés, a pályát húzzuk, azon pedig „szokásosan” gördül a kerék. Vegyük észre, hogy az így megfogalmazott feladat azonos azzal, mintha nem a pályát mozgatnánk, hanem saját magunkat, a megfigyelőt, tehát egy teljesen hagyományos cikloisról beszélnénk, csak épp úgy, hogy közben a megfigyelő is odébb megy.
Nagyobb problémát jelent a kérdés megértésénél, hogy mégis pontosan mi kell, hogy egyenes legyen. A zavart elsősorban a „talppont”, „tetőpont” és – különösen – a „dislokációs egyenes” szavak használata okozza, melyeket a levél sehol nem definiál. Első ránézésre az ember azt gondolhatná, hogy ezeket minden bizonnyal Beke Manó használta a levél által is hivatkozott könyvében [3]. Bár ez nagyon kézenfekvő magyarázat lenne, sajnos nem igaz: a 6. ábra mutatja Beke könyvének cikloisról szóló részét, pontosan abból az 1920-as második kiadásából, amit a levél alapján József Attiláék is olvastak. Jól látható, hogy a nem definiált kifejezések egyike sem szerepel benne.

6. ábra. Facsimile oldalak Beke Manó Bevezetés a differenciál- és integrálszámításba könyvének azon kiadásából, amelyre József Attila és Pákozdy Ferenc levele hivatkozik.
Magunkra vagyunk tehát utalva, hogy kiválasszuk a megfelelő értelmezést. A legvalószínűbb talán a következő: a talppont a kerék talajjal érintkező pontja a gördülés megkezdésekor (tehát a ciklois kiindulópontja), a tetőpont a ciklois legmagasabb pontja, tehát a nyomon követett pont helye egy fél kerékfordulat után, a „dislokációs egyenes” pedig egyszerűen a kettőt összekötő egyenes.
Ha így definiáljuk, akkor a probléma nagyon egyszerűen megoldható, csak egy dologra kell odafigyelnünk.
Ha pálya a húzás révén 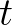 időben
időben 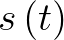 távolsággal van eltolódva (a pozitív szám jelentse a koordinátarendszer előjelével egyezően a jobbra mozgatást), akkor a görbe paraméteres egyenletrendszere nyilván:
távolsággal van eltolódva (a pozitív szám jelentse a koordinátarendszer előjelével egyezően a jobbra mozgatást), akkor a görbe paraméteres egyenletrendszere nyilván:
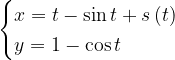
Ahhoz, hogy ez épp egy egyenes legyen, az 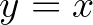 egyenlőségnek kell megvalósulnia. (Természetesen nyugodtan mondhattunk volna
egyenlőségnek kell megvalósulnia. (Természetesen nyugodtan mondhattunk volna 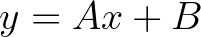 egyenlőséget is, de részint érezhető, hogy ez – pusztán lineáris átskálázás révén – érdemi újdonságot nem fog hozni, csak a jelöléseket bonyolítja, részint a kérdés pozitív megválaszolásához nekünk elég egy egyenest mutatnunk.) A megoldandó egyenlet tehát:
egyenlőséget is, de részint érezhető, hogy ez – pusztán lineáris átskálázás révén – érdemi újdonságot nem fog hozni, csak a jelöléseket bonyolítja, részint a kérdés pozitív megválaszolásához nekünk elég egy egyenest mutatnunk.) A megoldandó egyenlet tehát:
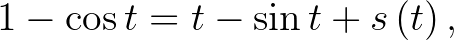
amiből

Ez egyáltalán nem volt nehéz, sőt, rögtön látszik, hogy minden létező paraméteres görbére egyszerűen megoldható ugyanilyen módon, a kérdés inkább csak az lehet, hogy ez a mozgás fizikailag realizálható-e. Ha például az 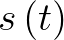 függvénynek szakadása van, akkor az nyilván nem lehet egy talaj tényleges mozgása, hiszen az nem tud pillanatszerűen „odébb ugrani”. Itt belefutunk abba, hogy mi a pontos definíciója annak, hogy „fizikailag realizálható”, mert amellett is lehet érvelni, hogy mondjuk a sebesség maga sem tud pillanatszerűen megváltozni.
függvénynek szakadása van, akkor az nyilván nem lehet egy talaj tényleges mozgása, hiszen az nem tud pillanatszerűen „odébb ugrani”. Itt belefutunk abba, hogy mi a pontos definíciója annak, hogy „fizikailag realizálható”, mert amellett is lehet érvelni, hogy mondjuk a sebesség maga sem tud pillanatszerűen megváltozni.
Szerencsénkre mind a szinusz-, mind a koszinuszfüggvény nem csak, hogy folytonos, de mivel a deriváltjaik is szinuszok és koszinuszok lesznek, így elmondható, hogy minden deriváltjuk is folytonos8. Mivel 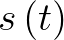 időbeli deriváltja lesz a talaj mozgatásának szükséges sebessége, annak deriváltja a szükséges gyorsulás, és így tovább, ha ez mind folytonos, akkor nyugodtak lehetünk afelől, hogy ez a mozgatása a talajnak – avagy, fordítva nézve, a megfigyelőnek – fizikailag realizálható.
időbeli deriváltja lesz a talaj mozgatásának szükséges sebessége, annak deriváltja a szükséges gyorsulás, és így tovább, ha ez mind folytonos, akkor nyugodtak lehetünk afelől, hogy ez a mozgatása a talajnak – avagy, fordítva nézve, a megfigyelőnek – fizikailag realizálható.
A 7. ábra mutatja az ahhoz szükséges talajsebességet és -gyorsulást, hogy a pont pályája egyenes legyen. A sebesség jórészt negatív, de gondoljuk végig, hogy ez teljesen logikus: mivel a kerék jobbra (pozitív irányba) gördül, így a talajt nyilván balra (negatív irányba) kell húznunk, hogy egyáltalán esélye legyen az 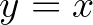 egyenesen maradnia a pontnak és ne „gördüljön ki” jobbra.
egyenesen maradnia a pontnak és ne „gördüljön ki” jobbra.
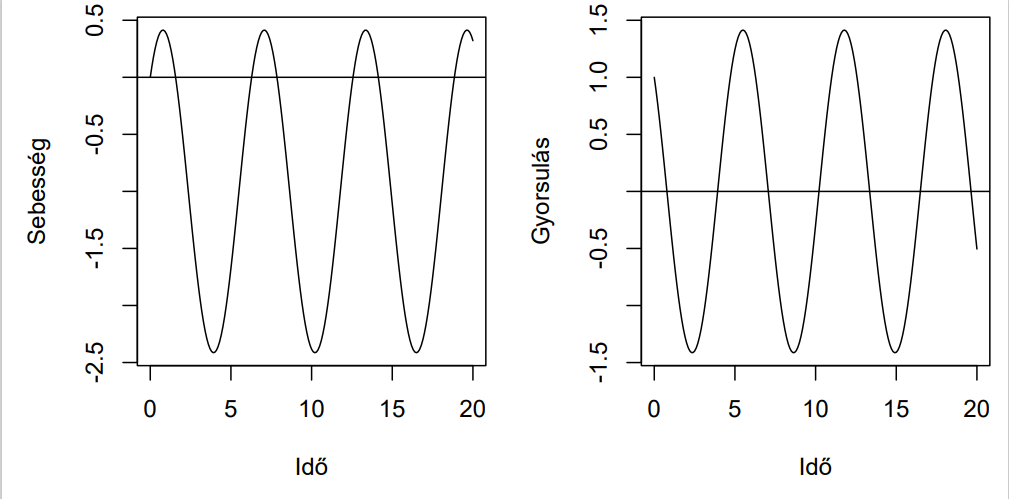
7. ábra. A József és Pákozdy levelében felvetett kérdésre választ adó talaj-mozgatás szükséges sebessége és gyorsulása.
Ha ezt kicsit nehéz is elképzelni, a https://www.github.com/tamas-ferenci/JozsefAttilaEgyMatematikaiKerdese oldal utolsó animációja segít, mert megmutatja a dolgot működés közben (azzal, hogy megfigyelőt mozgatja, nem a talajt, de mint már volt róla szó, ez természetesen egyenértékű).
4. Konklúzió
„Vasútnál lakom. Erre sok
vonat jön-megy és el-elnézem,
hogy’ szállnak fényes ablakok
a lengedező szösz-sötétben.
Igy iramlanak örök éjben
kivilágított nappalok
s én állok minden fülke-fényben,
én könyöklök és hallgatok.”
(József Attila: Eszmélet XII.)
József és Pákozdy kérdésére tehát egyfelől igenlő válasz adható, másrészt viszont a megvalósítás nem az, amit a levélben leírtak. Minden valószínűség szerint félreérthettek valamit, bár arra nem sikerült rájönnöm, hogy mit (az világos, hogy az 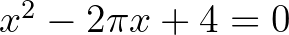 egyenletet megoldva keresték a választ).
egyenletet megoldva keresték a választ).
Első ránézésre meglepőnek tűnhet, hogy József Attila levelezésében egyáltalán ilyet találni. Valójában annyira nem meglepő, de ennek megértéséhez tegyünk egy lépést hátra, és nézzük átfogóbban a kérdést – hogyan viszonyult József Attila a matematikához? Ott kezdeném, hogy József a makói gimnáziumban, ahová 1920-tól '23-ig járt, kiváló volt matematikából, az, hogy érettségi jegye „jó” lett, inkább annak köszönhető, hogy milyen körülmények között érettségizett. Testvére, József Jolán, az Attiláról írt életrajzi regényében, A város peremén című könyvében még külön ki is tér erre: „Mennyiségtanban különösen kiváló képességeket árult el, tanára később váltig biztatta, hagyja az irodalmat, foglalkozzon matematikával” [17, 123.o.]. József Jolán írása szerint, amikor később „felforgató tevékenysége” miatt – azaz, hogy Ady Endrét szavalt az önképzőkörben – felvenni sem akarták a következő évfolyamra, mennyiségtantanára ezt mondta: „Ilyen koponya évtizedek alatt sem bukkan föl gimnáziumunkban! Micsoda matematikus lehetne belőle! Barátaim, egy nagy tudós…” [17, 132–133.o.]. (Hozzá kell azért tenni, hogy József Jolán műve eléggé ki van színezve, ennél az esetnél ráadásul Jolán jelen sem lehetett.)
József Attila rövid szegedi egyetemi tanulmányai szintén alátámasztják természettudományos érdeklődését: indexének tanúsága szerint [32], noha magyar–francia–filozófia szakra járt, felvette Ortvay Rudolf Az anyag korpuszkuláris elmélete és Kiss Árpád Az atomok és molekulák szerkezete című kurzusait. A tematikák alapján az előbbi kurzuson bizonyosan hallott az akkor legkorszerűbb kvantumfizikai ismeretekről, az utóbbi pedig a radioaktivitást járta körül [9]. (1924-ben a kvantumfizika „régi kvantumelmélet” érája nagyjából lezárt volt, és erről Ortvay minden bizonnyal átfogóan tudott beszélni, hiszen maga is a legnagyobbaktól tanult, például Arnold Sommerfeldtől9 Münchenben. A radioaktivitás bemutatása azonban mindenképp nagyon hiányos kellett legyen, hiszen a neutront majd csak 1932-ben fogja felfedezni Chadwick, a nélkül pedig bajos a radioaktivitást bármilyen közelítéssel is elmondani.) József Attila ezeken túlmenően a relativitáselméletről is hallott; Gazda István alaposan feltárta, hogy mi lehetett ezen tudásának a forrása: minden bizonnyal Fényes Samu, ismeretterjesztőnek is kitűnő író, ügyvéd cikkei [8, 9]. Tverdota György József kozmológiai ismeretei lehetséges forrásainak járt utána egy írásában [35], több közlemény, köztük Marx Györgyé pedig általában a modern fizikával való érintkezését mutatta be [23, 30, 34].
A fentiek fényében talán nem annyira meglepő, hogy a most tárgyalt kérdésen kívül valójában van még egy, jól dokumentált esete József Attila matematikai érdeklődésének! Bécsi tartózkodása alatt, 1926. januárjában levelet írt Galamb Ödönnek, aki a makói gimnáziumban tanára – és egyben pártfogója – volt. Ez a fizikusok számára is érdekes lehet, hiszen egy helyen ezt írja benne: „Ezek az anyagi okok nálam azt idézik elő, hogy más etikai síkon nyilvánuljon meg az általuk jelen körülmények között elfojtott erő (betörés, gyilkosság, szélhám), hanem életemet befelé irányítják s előáll, de pszihikai kvalitásban az az Einstein állította eset, hogy t. i. egy bizonyos sebességi erő hat egy bizonyos testre s ha az erő akkora, hogy a sebességi határnál (300.000 km. sec.‒1) nagyobb gyorsasággal kéne haladnia a testnek, akkor az erő maga is átalakul anyaggá. Ez az anyag vagyok én és ez az erő vagyok én.” [6, 90.o.]. (Ebből is érzékelhető, hogy József egyrészt nem értette meg pontosan az einsteini állítást, másrészt, hogy a hozzáállása inkább misztikus, és szabadon használja a felszínes, sőt, pusztán verbális hasonlóságokon alapuló analógiákat.) Fizikusok számára valószínűleg megdöbbentőbb a következő rész, ugyanebből a levélből: „t. i. a mi univerzumunk a pozitiv és negativ elektrónok rendszere, és a másik jelenlevő univerzum pedig azoké, melyekhez képest a jelen ismert negativok – pozitivok; illetve a jelen ismert elektrónok pozitiv és negativ egyedei által alkotott rendszer – pozitiv rendszer és ennek megfelelően van negativ rendszer is”. Az előbbi megjegyzés fényében valószínűleg nem érdemes túlértelmezni ennek a jelentőségét, de azért enyhén szólva is meghökkentő a dolog: Dirac csak 1928-ban, azaz két évvel e levél után vetette fel először az antielektronok létét! Amit aztán csak 1932-ben, hat évvel József Attila levele után igazolt egyértelműen Carl David Anderson kísérletesen is. Toró Tibor egész cikket szentelt e kérdés vizsgálatának, melyben alaposan körüljárja a kapcsolódó fizikai ismereteket is [32]. (Bár hozzá kell tenni, hogy jelen sorok szerzője szerint néhol már kissé a József Attila-i viselkedés inverzébe esve, nem a természettudományhoz kötve felszínes analógiákkal művészetet, hanem a művészethez kötve felszínes analógiákkal természettudományt: „Visszatérve a CP-sértés problematikájához, van tehát egy megmaradási törvény, a CP-paritás megmaradása, amely 99,8 százalékban érvényes, de ugyanakkor a K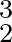 mezon két pi-mezonos bomlásánál a megmaradási törvény szerkezete fellazul és szisztematikusan 0,2 százalékos, nagyon kicsiny CP-sértés lép fel. Következésképpen a „törvény szövedéke itt, egy kicsit fölfeslik”, de csak 0,2 százalékosan, 99,8 százalékban továbbra is érvényben marad.” [32, 92.o.].)
mezon két pi-mezonos bomlásánál a megmaradási törvény szerkezete fellazul és szisztematikusan 0,2 százalékos, nagyon kicsiny CP-sértés lép fel. Következésképpen a „törvény szövedéke itt, egy kicsit fölfeslik”, de csak 0,2 százalékosan, 99,8 százalékban továbbra is érvényben marad.” [32, 92.o.].)
De nézzük most a matematika szempontjából érdekes részt! Ugyanezen levélben ezt írja: „Az 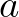 egyenes hossza:
egyenes hossza: 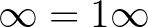 . A
. A 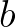 görbe hossza:
görbe hossza: 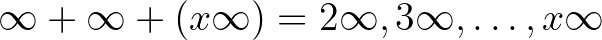 . Tehát a
. Tehát a 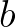 görbe hossza legalább 2 végtelennél több. T.i. vedd magadat tengelynek, akkor ha jobbról indul a görbe balra, éppen mert görbe, vissza is tér, akkor is, ha szabálytalan és a visszatérés is legalább
görbe hossza legalább 2 végtelennél több. T.i. vedd magadat tengelynek, akkor ha jobbról indul a görbe balra, éppen mert görbe, vissza is tér, akkor is, ha szabálytalan és a visszatérés is legalább 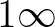 , amennyi az odahaladás. Ez azután geometriailag igazolja, hogy van 1. 2. 3. … x. rendű végtelen és így zérus. Három pont, két egymást metsző egyenes (tehát összetartó, párhuzamos) vagy 1 görbe meghatároz egy síkot. (Azt hiszem nem mondták még ki ezt a kézenfekvő dolgot a görbével.) No most, ha az egyenes mozog, nem a saját irányában, síkot alkot. A mozgás egy speciális esete a forgás, ha idegen tengely körül történik, szintén síkot alkot. No most képzelj el egy parabólát forgó mozgásban, még pedig úgy, hogy a mozgási tengely a szárainál, a végtelenben van. Tehát: [8. ábra] Ekkor szintén »sík«jön létre, amely sík zárt egész, s amely síknak vetületei, az engem érdeklö helyzetben: [8. ábra] Ez a »zárt sík«, ha az A tengely körül forog, korongalaku testet kapunk, míg ha a B tengely körül forog, egyáltalában nem kapunk testet. Ami azt hiszem, azt bizonyítja geometriailag, hogy van abszolút zérus, tehát a 0 értékek sorozatának limese. T.i. a pontnak nincs kiterjedése, 2 pontnak szintén 3nak szintén nincs kiterjedése, tehát
, amennyi az odahaladás. Ez azután geometriailag igazolja, hogy van 1. 2. 3. … x. rendű végtelen és így zérus. Három pont, két egymást metsző egyenes (tehát összetartó, párhuzamos) vagy 1 görbe meghatároz egy síkot. (Azt hiszem nem mondták még ki ezt a kézenfekvő dolgot a görbével.) No most, ha az egyenes mozog, nem a saját irányában, síkot alkot. A mozgás egy speciális esete a forgás, ha idegen tengely körül történik, szintén síkot alkot. No most képzelj el egy parabólát forgó mozgásban, még pedig úgy, hogy a mozgási tengely a szárainál, a végtelenben van. Tehát: [8. ábra] Ekkor szintén »sík«jön létre, amely sík zárt egész, s amely síknak vetületei, az engem érdeklö helyzetben: [8. ábra] Ez a »zárt sík«, ha az A tengely körül forog, korongalaku testet kapunk, míg ha a B tengely körül forog, egyáltalában nem kapunk testet. Ami azt hiszem, azt bizonyítja geometriailag, hogy van abszolút zérus, tehát a 0 értékek sorozatának limese. T.i. a pontnak nincs kiterjedése, 2 pontnak szintén 3nak szintén nincs kiterjedése, tehát 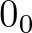 ,
, 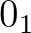 ,
, 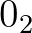 ,
, 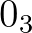 , …, ahol a
, …, ahol a 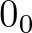 geometriai értékét a fentebb, a B tengely körüli forgás eredménye jelzi. (A pontnak nincs kiterjedése, ezért nem foroghat a »saját tengelye« körül, mely esetben az eredmény ugyanaz volna.)” [12, 94.o.].
geometriai értékét a fentebb, a B tengely körüli forgás eredménye jelzi. (A pontnak nincs kiterjedése, ezért nem foroghat a »saját tengelye« körül, mely esetben az eredmény ugyanaz volna.)” [12, 94.o.].
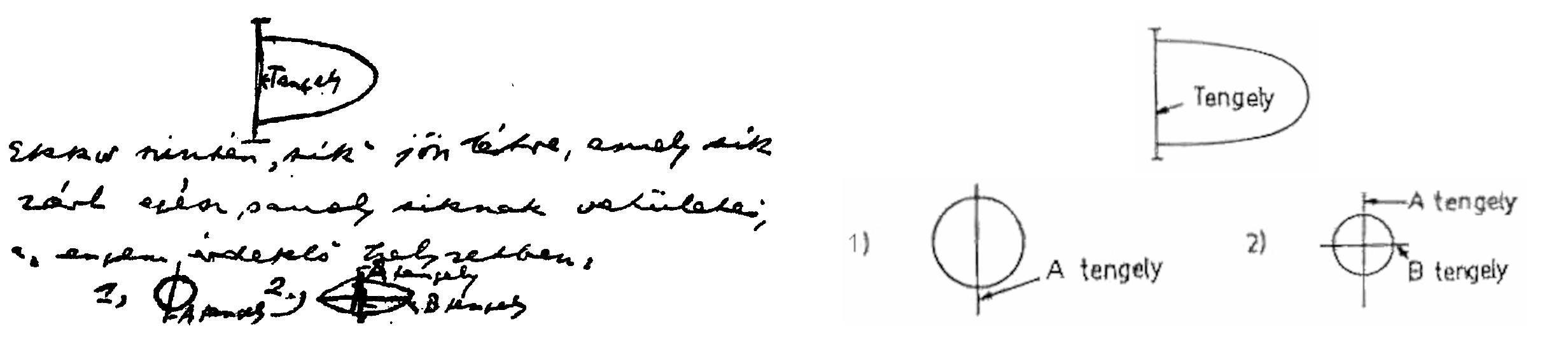
8. ábra. József Attila levelének facsimile részlete (balra) és a válogatott levelezésben található stilizált ábrák (jobbra).
Ezen gondolatok elemzését meg a parabola forgatását meghagyom egy másik írás tárgyának, de azt hiszem ennyiből is érzékelhető, hogy a matematikában is érvényesülnek a fizikában korábban mondottak, hogy ti. József egy sor fogalmat nem pontosan használ, és a kiinduló koncepciókat szabadon alakítja úgy, mintha a szavak egymás után fűzése egyúttal matematikai levezetés, illetve bizonyítás is lenne. (Valójában a sík görbületére vonatkozó gondolatait is valószínű, hogy a relativitáselmélet nagyon naiv értelmezései adták.) A magabiztossága ugyanakkor e tekintetben is olyan, mint a korszak több más leveléből is érződik; 1926 februárjában ezt írja Jolán nővérének: „a szabálytalan görbékre vonatkozó fejtegetéseimmel erős lökést adtam a geometriának” [12, 98.o.].
Amiért mégis ide idéztem a dolgot, azon túl, hogy a diszkusszió teljességéhez hozzá tartozik, egy későbbi fejlemény ezen idézet kapcsán. A már említett Galamb Ödön, József Attila makói tanára és pártfogója 1941-ben könyvet adott ki Józseffel kapcsolatos emlékeiről, Makói évek címmel. A könyvben Galamb felidézi ezt a levélváltásukat is, viszont érzékeli, hogy a tartalmát nemigen tudja megítélni (Galamb latin-történelem-gyorsírás tanár volt, József Attilának görögpótló10 irodalmat tanított [25]), úgyhogy erre tekintettel a lehető legfelelősebb döntést hozta, és inkább kikérte egy hozzáértő, Kun-Kuti Márton matematikatanár-társa véleményét. (Bár ma is így járnának el a könyvek és újságok szerzői hasonló helyzetben…) Kun-Kuti pontokba foglalva fogalmazta meg észrevételeit; véleményem szerint 80 év távlatából is helytálló, tanulságos módon:
„ – A valóságtudományok szakemberei – az eredményért való felelősségük tudatában – nagy gonddal vigyáznak arra, hogy állításaik a bizonyíthatóság kereteit ne lépjék túl. Ez pedig a szabadon csapongani szerető fantáziát oly nagy mértékben korlátozza, hogy az eredmény rendszerint nagyon szerény.
– Egészen más a helyzet az ú. n. művészlelkű embereknél. Az ő fantáziájuk szabadon csaponghat. Nem korlátozza semmi. Ezért van az, hogy az írók, költők, művészek fantáziája a dolgok lényegének oly mélységeire is rátapint néha, ahova a bizonyíthatóság keretein belül maradó ész talán soha sem juthat el. Egyes írók – pl. Verne, Jókai – oly gépekről írtak részletesen, melyeket később találtak fel. Vagy a valóság titkairól néha oly elgondolásokat nyilvánítottak, melyeket a tudomány később igazolt.
– Ilyen szabadon csapongó fantáziájú, erős intuíciójú művészlélek volt József Attila is. […]
– Egy másik helyen igen érdekes – de nem új – matematikai problémát fejteget… A sík végtelen sugarú gömb felületeként fogható fel. A gömbfelület görbe. A sík nem görbe. Mégis a kettő azonosítható. Ezért kérdezi: – Van-e görbe sík? – Itt nyilván; a van alatt fogalmi és nem tárgyi létezésre gondol.
– Fejtegeti a végtelen problémáját. Mint a legtöbb nem szakember, ő is a végtelent valami misztikus színezetű, észfölötti távolságok homályába vesző, konkréten létező objektumnak tekinti. Nem gondolva arra, hogy a matematikus a végtelen alatt nem valami ténylegesen létező objektumot, hanem pusztán csak végnélküliséget ért, azaz pl. egy végtelen sorozatnál annyit és csak annyit ért alatta, hogy akármily távoli tagot szemelünk is ki, azon túl a sorozatnak még van tagja. Tehát a végtelen csak egy – az emberi értelmet túl nem lépő – tulajdonság a matematikában, melynek létmódja az érvényesség és nem a tárgyi létezés. Valószínűleg ez az oka annak, hogy a végtelen, nagy és végtelen kicsi számmal éppen úgy szoroz, mint a közönséges számokkal, pedig végtelen nagy és végtelen kicsi szám voltaképpen nincs is.
– A tárgyi precizitás részleteitől eltekintve elmélkedései mélyre tapintó érdekes gondolatokat tartalmaznak, melyek a valóság megismeréséért évezredek óta világszerte folyó óriási szellemi küzdelemnek több legizgatóbb problémáját érintik” [7, pp. 71–73].
Ha már úgyis emlegettem korábban József Jolán regényét, nem tudom megállni, hogy egy roppant érdekes momentumra fel ne hívjam a figyelmet ezen a ponton. Kun-Kuti előbbi véleménye Jolán művében is megjelenik – csak épp abban Rákosi Mátyás mondja! József Jolán ideologikusan nagyon terhelt regényében11 ugyanis a fiatal Rákosi találkozik József Attilával, sőt – minő véletlen – a találkozás „éles fordulatot jelentett Attila szellemi fejlődésében”, és „Marx gazdasági tanainak, a marxi történelemfilozófiának ismeretét ekkor kapta útravalóul” [17, p. 166]. (Az egyébként elképzelhető, hogy József Attila és Rákosi tényleg találkozott, de az összes többi már az 1948 utáni kommunista rendszer primitív, propagandisztikus kitalációja. Helyenként abszurdba hajló mozzanatokkal tarkítva: József Jolán, mint újságíró 1949-ben interjút készített Rákosi Mátyással, ami az országgyűlési választások napjára időzítve jelent meg, ebből megtudjuk, hogy a jóságos Rákosi még a börtönből is egyengette József Attila útját… [15]. Szőke György izgalmas cikkben járt utána annak, hogy mindebből mi lehet igaz [31].) József Jolán regénye szerint Makai Ödönt, Attila sógorát – egyben gyámját, és a történet időpontjában szállásadóját – látogatja meg Rákosi, akinek Makai ezt mondja: „Éppen a végtelen problémáját fejtegette az ifjú. Úgy sejtem – nézett Attilára –, azt akartad bizonyítani, hogy a végtelen valami észfölötti távolságok homályába vesző, valóságban létező objektum.”, mire Rákosi azt válaszolja: „A végtelen csak egy tulajdonság a matematikában. Létmódja az érvényesség, nem pedig a tárgyi létezés.”. Azaz: József Jolán fogta a makói matematikatanár véleményét, és a bölcs Rákosi Mátyás12 szájába adta! (Azzal a már-már mókás módosítással, hogy valójában még Makai Ödön szabatosan megfogalmazott felvetésének a megszövegezését is Kun-Kutitól kölcsönözte…) Természetesen az időpontok sem stimmelnek, hiszen ekkor a regényben József még el sem utazott Bécsbe, márpedig, mint láttuk, a valóságban egy onnan írt levelében vetette fel először ezt a problémát.
Még egy érdekes „kapcsolódási pontot” hadd említsek meg József Attila és a matematika között. Egy pillanatra visszaadom a szót Tverdota Györgynek, amint az Eszmélet keletkezését datálja: „ha nem feltételezzük, hogy a XII. szakaszt 1934 júliusában vagy augusztusában, Budapestre, a Korong utcába való 1934. július 1-je táján történt visszatérése után írta, akkor a »Vasútnál lakom«– kijelentést korrekt módon csak Hódmezővásárhelyen történt ideiglenes letelepedése, 1934. március 1-je előtt és Szántó Judittal a Korong utcába költözésük (valószínűleg 1933. október) után tehette” [36, 15.o.]. Mint az ebből is kiderül, József Attila, ha megszakításokkal is, de többször élt a Korong utcában; egész pontosan a Korong utca 6. szám alatt. Ha valaki elzarándokol erre a címre, akkor csakugyan megtalálja József Attila emléktábláját a házon. De megtalál egy másik emléktáblát is… (9. ábra).

9. ábra. A Korong utca 6. szám alatti emléktáblák együtt (felül) és a két emléktábla közelebbről (alul).
Bizony ám, pontosan ugyanabban a házban lakott Arany Dániel, mint József Attila! Bóra Eszter alapos tanulmányban mutatta be13 Arany Dániel életútját [5], kitérve a Józseffel való kapcsolatára is: „Arany Dániel 1896-ban Budapesten épített egy villát, ez a mai napig áll a körvasúton túl Zuglóban a mai Korong utca 6. szám alatt. Ebben a csodálatos villa-lakásban élt és dolgozott a nagy műveltségű, széles érdeklődésű matematikus. A ház érdekessége, hogy 1933–1936 között József Attila bérelt benne egy szerény padlásszobát, »a város peremén«. Nem ismert, hogy a költő kitől bérelte a kis szobát, de annyi biztos, hogy ismerték egymást a matematikussal. [5, CLIV.o.], bár sajnos ez utóbbi állítást nem részletezi a cikk. (Feltűnő lehet az emléktábláról, hogy Arany Dániel halálának a dátuma nem ismert pontosan. 1944-ben gettósították Arany Dánielt zsidó származása miatt – jellemző adalék, hogy még ekkor is hazájára és a matematikára gondolt: gyorsan elajándékozta hatalmas könyvtárát az Eötvös Loránd Matematikai és Fizikai Társulatnak, hogy a háború utáni újrakezdésnél legyen szakirodalma az országnak; ezek a könyvek egyébként máig fellelhetőek a BME Matematikai Intézetének könyvtárában – és a gettót nem élte túl. A magyar matematikatanítás egyik legnagyobb alakját, a Középiskolai Matematikai Lapok megalapítóját úgy pusztították el feleségével együtt, hogy még a halálának pontos dátuma sem ismert, hamvai jeltelen sírban nyugszanak.)
Nagyon sokat beszéltünk József Attiláról, de mi a helyzet Pákozdy Ferenccel? Az ő életéről, és természettudományos érdeklődésről jóval kevesebb forrással rendelkezem (valószínűleg jóval kevesebb is áll rendelkezésre), de ennek ellenére egyáltalán nem meglepő, hogy a kérdést felvető levélnek ő is szerzője. Pákozdy ugyanis, amellett, hogy maga is költő és műfordító volt, és – mint a Tverdota idézetből is kiderült – József Attila barátja és hódmezővásárhelyi körének tagja, meglehetősen polihisztor alkat volt: eredetileg orvosnak tanult, aztán jogot végzett, dolgozott jegyzőként, levéltárosként majd évtizedekig könyvtárosként, mindemellett kitűnő sakkozóként is ismerték [1, 18].
Kitérő megjegyzés Pákozdy kapcsán: talán többen tudják, hogy történetesen – és teljesen véletlen egybeesésként – Pákozdy Ferencnek hívták azt a költőt is, akinek az 1933-ban a Társadalmi Szemlében megjelent kritikája, melyben azt írta, hogy a „magyar proletárirodalom sok problémája uj problémával szaporodott: József Attilával” szerepet játszott József Attila és az illegális kommunista párt kapcsolatának megromlásában. (Pákozdy, mármint a bántó kritikát író Pákozdy14 számára érhető módon elég kellemetlenné vált15 később ez az írás, 1954-ben azzal magyarázkodott Révai Józsefnek, hogy valójában nem gondolta így a leírtakat, csak az újság szerkesztőinek, Madzsar Józsefnek és Sándor Pálnak a nyomására jelentette meg a kritikát, akik arra hivatkoztak, hogy József Attila elítélése „a párt kívánsága” [21]. Érdekes adalék, hogy Sándor Pál egy 1964-es írásában ezt kategorikusan tagadta: „1. Én a Pákozdy által említett megbeszélésen nem vettem részt. 2. Sem Pákozdy, sem a Társadalmi Szemle egyetlen munkatársa előtt sem hivatkoztam soha arra, hogy »ez a párt álláspontja«. […] 3. Pákozdy levele szerint azon a beszélgetésen Madzsar vitte a szót és elsősorban saját kifogásait hozta fel a József Attila magatartásával kapcsolatban és fejtette ki véleményét a megírandó cikkre vonatkozólag.” [28]. Madzsar nem volt abban a helyzetben, hogy tiltakozzon, ugyanis az anya- és csecsemővédelem hazai megszervezőjét, a honi népegészségtan egyik legnagyobb alakját addig zaklatta a Horthy-rendőrség (Madzsar illegális kommunista volt), amíg a Szovjetunióba emigrált – ahol meg aztán két év után utolérte a sztálini tisztogatás: a kommunista pribékek minden nyom nélkül eltüntették, a mai napig még csak azt sem tudni, hogy egyáltalán hol vagy mikor halt meg. Madzsar helyett azonban a lánya, Lili beszállt a ringbe: „Apám 1945 után már nem élt, s Sándor Pál – kihasználva a lehetőséget – úgy védekezett, ahogy tudott. Azt állította, hogy a cikk megírásához neki nem volt köze, arra édesapám adta a megbízatást. Ezt a tényekkel határozottan meg lehetett cáfolni, hiszen apám a cikk megjelenését megelőző hónapokban börtönben volt, s minthogy eléggé rossz egészségi állapotban volt, idejött hozzánk Kassára, s egy ideig itt tartózkodott.” [22]. Ezt meg Sándor vitatja [28, 38], szóval mondhatjuk, hogy a kör bezárult…
5. Zárszó
Ha az írásom elején nagyon szubjektív voltam, hadd legyek a végén is az. Az Eszmélet nem olyan, mint a többi – szerintem – nagyon szép József Attila vers, a Tiszta szívvel, a Thomas Mann üdvözlése vagy az (Ime, hát megleltem hazámat). Sokszor kell elolvasni. Nem „érti” az ember elsőre, de ahogy újra és újra elolvassa, egyre közelebb kerül hozzá, míg egyszer csak azt nem veszi észre, hogy libabőrös lesz, ahogy az utolsó sorok végére ér.
Ferenci Tamás
Köszönetnyilvánítás
Mindenekelőtt hálás köszönetemet szeretném kifejezni Tverdota Györgynek (ELTE BTK Modern Magyar Irodalomtörténeti Tanszék): számomra már az is rendkívül megtisztelő, hogy az egyik legnagyobb József Attila-kutató vette a fáradságot, és egy hozzám hasonló teljes kívülálló írását egyáltalán elolvasta. Tverdota György azonban ennél sokkal többet tett, részletes magyarázattal szolgált számomra József Attila matematikai érdeklődése és ismeretei kapcsán; a Konklúzió fejezet idevágó részét teljes egészében az ő útmutatása alapján kutattam fel és írtam meg. Köszönöm Maczák Ibolyának (PPKE BTK Magyar Irodalomtudományi Tanszék) a segítőkészségét, és hogy több forrásra is felhívta a figyelmemet Pákozdy Ferenc (József Attila barátja...) kapcsán. Köszönöm Tóth Jánosnak (BME TTK Analízis Tanszék) a nagyon kedves szerkesztői munkát, és különösen, hogy felhívta a figyelmemet a Korong utca 6. szám alatti emléktáblapárra.
Dr. Ferenci Tamás klinikai biostatisztikus, az Óbudai Egyetem Élettani Szabályozások Kutatóközpontjában habilitált egyetemi docens. Emellett a Budapesti Corvinus Egyetem Statisztika Tanszékének félállású docense, és a Semmelweis Egyetem Népegészségtani Intézetének óraadó oktatója.
Irodalomjegyzék
[1] Bata Imre. A vásárhelyi poéta. Pákozdy Ferenc emlékezete.Tiszatáj, 31(4):72–76, 1977.
[2] Beke Manó. Determinánsok. Athenaeum Irodalmi és Nyomdai R.-T., 1915.
[3] Beke Manó. Bevezetés a differenciál-és integrálszámításba: a Népszerű Főiskolai Tanfolyam 1906-ik évi II. sorozatában tartott előadások. Franklin-Társulat, 2 edition, 1920.
[4] Beney Zsuzsa. Az eszmélet lírája. Tiszatáj, 43(1):60–69, 1989.
[5] Bóra Eszter. Ismeretlen ismerősünk: Arany Dániel. Természet Világa, 140(10):CLI–CLV, 2009.
[6] Fehér Erzsébet. József Attila válogatott levelezése. Akadémiai Kiadó, 1976.
[7] Galamb Ödön. Makói évek. Cserépfalvi, 1941.
[8] Gazda István. Einstein relativitáselméletének első hazai interpretátorai. Magyar Tudomány, 24(6):476–483, 1979.: http://real.mtak.hu/19206/1/gazda_MATUD_1979.pdf.
[9] Gazda István. József Attila és a relativitáselmélet. Kritika, 80(3):4–6, 1980.
[10] Izrail Moiseevitch Gelfand and Sergei Vasilyevich Fomin. Calculus of variations. Courier Corporation, 2000.
[11] Szemjon Grigorjevics Gingyikin. Történetek fizikusokról és matematikusokról. Typotex, 2004.
[12] H. Bagó Ilona, Hegyi Katalin, Stoll Béla. József Attila levelezése. Osiris Kiadó, 2006.
[13] Járai Antal. Modern alkalmazott analízis. Typotex, 2007.
[14] David C. Johnston. Cycloidal paths in physics as superpositions of translational and rotational motions. American Journal of Physics, 87(10):802–814, 2019. http://aapt.scitation.org/doi/10.1119/1.5115340.
[15] József Jolán. Rákosi Mátyás József Attiláról. Szabad Nép, 7(112):11, 1949.
[16] József Jolán. József Attila élete. Szépirodalmi Könyvkiadó, 1955.
[17] József Jolán. A város peremén. Móra Ferenc Könyvkiadó, 1975.
[18] Kenyeres Ágnes. Magyar életrajzi lexikon. Akadémiai Kiadó, 1994.
[19] Kósa András. Variációszámítás. Tankönyvkiadó, 1973.
[20] Kőszegfalvi Ferenc. Pákozdy Ferenc (1904–1970) bibliográfia, 2003.
[21] Legát Tibor. József Attila esete a két Pákozdy Ferenccel, akik szintén költők voltak. Magyar Narancs, 2020. https://magyarnarancs.hu/sorkoz/jozsef-attila-esete-a-ket-pakozdy-ferenccel-akik-szinten-koltok-voltak-128728 (elérés dátuma 2020. 10. 06.).
[22] Madzsar Lili. Madzsar Lili visszaemlékezése. Palócföld, 22(6):51–59, 1988.
[23] Marx György. A modern fizika forradalma és József Attila. Új írás, 21(2):66–70, 1981.
[24] Nobel Prize organisation. Nomination archive – Arnold Sommerfeld, 2020. https://www.nobelprize.org/nomination/archive/show_people.php?id=8661 (elérés dátuma 2020. 10. 16.)
[25] Péter László. József Attila közöttünk. Somogyi-könyvtár, 1980.
[26] Reiman István. A geometria és határterületei. Gondolat, 1986.
[27] Rózsa Pál. Bevezetés a mátrixelméletbe. Typotex, 2009.
[28] Sándor Pál. József Attila és az illegális kommunista párt. Kritika, 80(3):7–9, 1980.
[29] George F Simmons. Differential equations with applications and historical notes. CRC Press, 2016.
[30] Simon Péter. “József Attila és a fizika”. Természet Világa 136.11 (2005), 495–498. old.
[31] Szőke György. „Akire csak a párt vigyáz...”. Forrás, 37(4):58–62, 2005. http://www.forrasfolyoirat.hu/0504/szoke.html
[32] Toró Tibor. József Attila transznegatívum-elmélete és az anyag-antianyag-szimmetria(sértés). Természet Világa, 137(I. különszám):88–92, 2006. : http://www.termeszetvilaga.hu/szamok/kulonszamok/k0601/toro.pdf.
[33] Tóth János, Simon L Péter. Differenciálegyenletek. Bevezetés az elméletbe és az alkalmazásokba.Typotex, 2020.
[34] Tuska Ágnes. “...a működésben van a nyugalom”. Fizikai Szemle 30.11 (1980), 430–434. old.
[35] Tverdota György. József Attila költészetének kozmológiai vonatkozásai. Irodalomtörténeti Közlemények, 83(2):121–133, 1979.
[36] Tverdota György. Tizenkét vers. József Attila Eszmélet-ciklusának elemzése. Gondolat, 2004.
[37] Valachi Anna. Három testvér – háromféle kísérlet az elveszett gyermekkor visszahódítására. Thalassa, 12(2-3):145–154, 2001. http://imago.mtapi.hu/a_folyoirat/e_szovegek/pdf/(12)2001_2-3/145-154_Valachi-A.pdf.
[38] Vértes György. József Attila és az illegális kommunista párt. Irodalomtörténeti Közlemények, 21(2):192–218, 1963.
[39] Robert Weinstock. Calculus of variations: with applications to physics and engineering. Courier Corporation, 1974.
Lábjegyzetek
- 1
- Azok számára, akik szeretnék saját kezűleg megvizsgálni ezt, a következő a fizikai levezetés. Vegyük fel a koordinátarendszerünk origóját a kezdőpontban, az
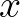 tengely mutasson vízszintesen jobbra, az
tengely mutasson vízszintesen jobbra, az 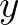 pedig függőlegesen lefelé. Mivel a golyó energiája kezdetben nulla, és a gravitáción kívül más nem hat rá, így
pedig függőlegesen lefelé. Mivel a golyó energiája kezdetben nulla, és a gravitáción kívül más nem hat rá, így 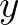 „magasságban” (mélységben)
„magasságban” (mélységben) 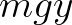 helyzeti energiát nyer; a súrlódás hiánya miatt ez teljesen egészében az
helyzeti energiát nyer; a súrlódás hiánya miatt ez teljesen egészében az 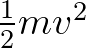 mozgási energiájává alakul. Azaz a sebessége, midőn a függőleges koordinátája
mozgási energiájává alakul. Azaz a sebessége, midőn a függőleges koordinátája 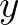 , épp
, épp  . Másrészről, egy piciny
. Másrészről, egy piciny 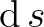 szakasz megtételéhez szükséges idő, ha épp
szakasz megtételéhez szükséges idő, ha épp 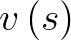 a golyó sebessége (ahol
a golyó sebessége (ahol 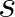 az indulási ponttól a pályán mérve megtett út) természetesen
az indulási ponttól a pályán mérve megtett út) természetesen 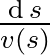 , így az egész út megtételéhez szükséges idő
, így az egész út megtételéhez szükséges idő 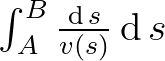 . Hogy áttérjünk
. Hogy áttérjünk 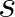 -ről
-ről 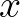 -re, kellene tudni, hogy
-re, kellene tudni, hogy 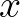 koordinátánál mennyi a pályán mért elmozdulás, ha egy kicsiny
koordinátánál mennyi a pályán mért elmozdulás, ha egy kicsiny 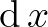 távolsággal odébb megyünk. Szerencsére ez analízisből ismert, hiszen lényegében egy ívhosszról van szó:
távolsággal odébb megyünk. Szerencsére ez analízisből ismert, hiszen lényegében egy ívhosszról van szó: ![$\operatorname{d}s=\sqrt{1+\left[y'\left(x\right)\right]^2} \operatorname{d}x$](/images/stories/latexuj/2020-11/2020-11-ferencitamasjozsefattila/img15.png) , ahol
, ahol 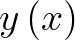 a rámpa alakja, mint függvény. Ezt behelyettesítve kapjuk, hogy a szükséges idő
a rámpa alakja, mint függvény. Ezt behelyettesítve kapjuk, hogy a szükséges idő ![$\int_0^b \frac{1}{\sqrt{2gy\left(x\right)}} \sqrt{1+\left[y'\left(x\right)\right]^2} \operatorname{d}x$](/images/stories/latexuj/2020-11/2020-11-ferencitamasjozsefattila/img17.png) , ha
, ha 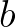 a
a 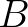 pont vízszintes távolsága
pont vízszintes távolsága 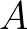 -tól. Kihasználtuk, hogy a golyó vízszintesen csak szigorúan
-tól. Kihasználtuk, hogy a golyó vízszintesen csak szigorúan 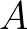 -ból
-ból 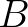 fele tud haladni (egy csak alátámasztást nyújtó rámpával nem tudjuk visszafordítani vízszintesen), így a teljes út integrálása megfelel az
fele tud haladni (egy csak alátámasztást nyújtó rámpával nem tudjuk visszafordítani vízszintesen), így a teljes út integrálása megfelel az 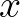 szerint 0-tól
szerint 0-tól 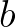 -ig történő integrálásnak. (Ha a görbénk paraméteresen adott, akkor a
-ig történő integrálásnak. (Ha a görbénk paraméteresen adott, akkor a ![$\int_{t_a}^{t_b} \frac{1}{\sqrt{2gy\left(t\right)}} \sqrt{\left[x'\left(t\right)\right]^2+\left[y'\left(t\right)\right]^2} \operatorname{d}t$](/images/stories/latexuj/2020-11/2020-11-ferencitamasjozsefattila/img21.png) alak használható, ahol
alak használható, ahol 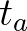 és
és 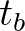 azok az értékek, amik között a paraméternek futnia kell, hogy megkapjuk a görbét
azok az értékek, amik között a paraméternek futnia kell, hogy megkapjuk a görbét 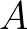 -ból
-ból 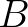 -be.) A feladat az, hogy megtaláljuk azt az
-be.) A feladat az, hogy megtaláljuk azt az 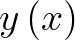 függvényt, ami ezt a kifejezést minimalizálja. Itt arról van tehát szó, hogy minden függvényhez hozzárendelünk egy számot, ezt szép néven funkcionálnak szokták hívni, és ezek körében minimalizálunk – keressük azt a függvényt, amihez rendelt szám a minimális. A matematika azon területét, ami ilyen szélsőérték-keresési feladatokkal foglalkozik, szokás variációszámításnak nevezni; a brachisztochron probléma a legelső történeti példák egyike variációszámításos feladatra [10, 13, 19, 33, 39].
függvényt, ami ezt a kifejezést minimalizálja. Itt arról van tehát szó, hogy minden függvényhez hozzárendelünk egy számot, ezt szép néven funkcionálnak szokták hívni, és ezek körében minimalizálunk – keressük azt a függvényt, amihez rendelt szám a minimális. A matematika azon területét, ami ilyen szélsőérték-keresési feladatokkal foglalkozik, szokás variációszámításnak nevezni; a brachisztochron probléma a legelső történeti példák egyike variációszámításos feladatra [10, 13, 19, 33, 39]. - 2
- Mindazonáltal néhány egyszerű alakú függvényre, például egyenesre, különböző kitevőjű hatványokra, különböző gyökökre, vagy akár paraméteresen adott görbékre, például körre, ellipszisre stb. érdekes lehet kiszámolni – ha lehet, analitikusan, ha nem, numerikusan – az integrált, és megnézni mit kapunk!
- 3
- Az ingánál konkrétan azt, hogy
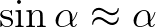 .
. - 4
- Fontos, hogy ez nem valamiféle triviálisan látható dolog, be kell bizonyítani, és az csak véletlen, hogy a ciklois alakú pályára kényszerítéshez épp ciklois alakú pofákra volt szükség. Azt, hogy adott alakú pofánál a rá felütköző fonál végpontja milyen görbét ír le, a pofa evolvensének nevezzük, megfordítva pedig azt mondjuk, hogy a pofa alakja az evolútája annak a görbének, amit a rá felütköző fonal végpontja leír. (Természetesen a matematikai definíciónál a gravitációra meg a felütközésre nincs szükség: azt mondjuk, hogy a fonalat mindig megfeszítve tartjuk.) Evolvensből végtelen sok van, attól függően, hogy milyen hosszú a fonál, evolútából viszont csak egy. A kérdés tehát az, hogy melyik görbének lesz az evolvense a ciklois, avagy fordítva megfogalmazva, mi a ciklois evolútája – és a válasz az, hogy a ciklois! De ismét hangsúlyozni kell, hogy ez csak véletlen, például a kör evolútája egy pont (gondoljuk végig!), az
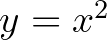 parabola evolútája az
parabola evolútája az 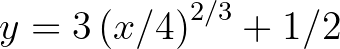 ún. Neil-parabola. Még csak az sem igaz, hogy a ciklois az egyetlen görbe ami saját maga evolútája, például a (logaritmikus) spirálnak szintén önmaga az evolútája.
ún. Neil-parabola. Még csak az sem igaz, hogy a ciklois az egyetlen görbe ami saját maga evolútája, például a (logaritmikus) spirálnak szintén önmaga az evolútája. - 5
- Igen, tudom, hogy a fizikus olvasók most a szívükhöz kapnak, hiszen így dimenzionálisan elromlanak az egyenletek. Itt most legyünk picit matematikusak.
- 6
- Ami egységnyi itt, azt a fizikusok úgy hívnák, hogy a forgás körfrekvenciája:
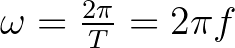 , ahol
, ahol 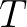 a periódusidő,
a periódusidő, 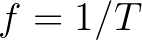 a frekvencia.
a frekvencia. - 7
- Tudjuk, hogy
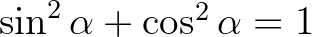 . Legyen
. Legyen 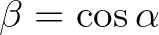 , és így
, és így 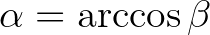 , ezt az előző egyenletbe helyettesítve kapjuk, hogy
, ezt az előző egyenletbe helyettesítve kapjuk, hogy 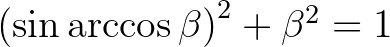 , ahonnan már adódik a felhasznált összefüggés.
, ahonnan már adódik a felhasznált összefüggés. - 8
- Analízises emberek úgy mondanák: végtelenszer folytonosan differenciálhatóak, avagy
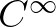 -beliek.
-beliek. - 9
- Sommerfeld a világ legpechesebb fizikusa, akit 1917 és '51 között összesen 84-szer jelöltek Nobel-díjra és egyszer sem kapta meg [24]. Amellett, hogy a saját jogán is kitűnő fizikus volt, hihetetlen volt a tehetségnevelése: hét tanítványából lett Nobel-díjas!
- 10
- Az 1924-es reformig így nevezték azokat a tárgyakat, amit a tanulók az 1890-ben eltörölt kötelező görög helyett tanultak a gimnáziumokban.
- 11
- József Jolán műve szívbemarkoló képet fest a '10-es, '20-as, '30-as évek rongyokban járó, éhező, poloskák között ablaktalan lyukakban tengődő munkásainak, cselédjeinek, nincstelenjeinek tömegeiről, és nem lehet kétségünk, hogy e kép megfelel a valóságnak, különösen, mert ezek Jolánnak is személyes élményein nyugszanak, ettől függetlenül a munkásmozgalom bemutatása még ezekben a részekben is zavaróan didaktikus a regényben. Jolán ráadásul, amellett, hogy egyéb esetekben is kever dátumokat, eseményeket, a József Attila-képet is érezhetően igyekszik sematikusan heroizálni (nem mintha erre József rászorulna). Csak egyetlen példa: a regényben Attila azért nem tér vissza a makói internátusba utolsó évében, 1922 őszén, mert „még a nélkülözést is inkább vállalja, mint hogy visszamenjen a megyei birtokosok és nagygazdák csemetéi közé” [17, pp. 132–133]. A valóságban József azért nem tudott visszamenni, mert 1922. június 26-án gyógyszerrel öngyilkosságot kísérelt meg, ami automatikus kicsapással járt, ezt egy korábbi diák példájából ő is tudhatta [7, pp. 21–25]. József Jolán könyvében azonban már csak azért sem derülhet ki ez az összefüggés, mert ő még az öngyilkossági kísérlet tényét is elhallgatja! Az ilyen torzítások jóval kevésbé – bár még így sem elhanyagolhatóan – voltak jelen Jolán tíz évvel korábban, 1940-ben írt, József Attila élete címet viselő könyvében [16]. Valachi Anna szerint, aki Jolánról József Jolán, az édes mostoha – Egy önérvényesítő nő a XX. század első felében címmel egész könyvet írt, az 1950-es regény megírására a Rajk-per alatt kapott pártmegbízást, és nem mert rá nemet mondani [37].
- 12
- 1975-ben újra kiadták József Jolán 1950-es regényét, de akkorra meg már Rákosi személye vált kellemetlenné. Jellemző a korabeli szocialista viszonyokra, hogy a problémát úgy hidalták át, hogy egész egyszerűen kihúzták a könyvből Rákosi nevét, de a személyét és a történetszálát nem, így az ezen kiadást olvasók csak arról értesülhettek, hogy József Attila egy név nélküli idegennel találkozik, aki alapvetően hat az életére…
- 13
- Bóra középiskolás diák volt a cikkének publikálásakor!
- 14
- Érdekességként megjegyzem, hogy a Wikipedia e sorok írásának pillanatában is azt írja a kritika kapcsán, hogy József Attila tudta, hogy az írás nem Pákozdy gondolatait tükrözi, mert korábban Pákozdy a Hétfői Újságban József Attila mellé állt. Igen ám, de a Hétfői Újság egy hódmezővásárhelyi lap volt, így – bár ez vegytiszta spekuláció a részemről – de elég gyanúsnak tűnik, hogy ez a Pákozdy valójában a másik Pákozdy volt, és így persze az egész okfejtés bukik. A keveredés nem lenne teljesen példátlan, vicces módon még a 2004-es kiadású Új Magyar Életrajzi lexikon hódmezővásárhelyi Pákozdyról szóló szócikkébe is bekerült hivatkozásként egy olyan cikk, ami valójában a másik Pákozdyról szól [20].
- 15
- Hogy „kellemetlenné vált”, az enyhe kifejezés, például az 1951-ben kiadott gimnáziumi tankönyvben ezt olvashatta Pákozdy saját magáról: „a kötettel kapcsolatban támadás érte [József Attilát] a munkásmozgalom egy szektáriánus, tehetségtelen költője részéről is”...