Matematika a díjak hátterében

Az MTA 197. közgyűlésének matematikus díjazottjai

A Magyar Tudományos Akadémia 197. Közgyűlésének ünnepi ülésén, illetve a Közgyűléshez kapcsolódó osztályrendezvényeken számos rangos tudományos díjat és elismerést adtak át. Ebben a cikkben röviden bemutatjuk a matematikus díjazottakat.

1. Akadémiai Díj

Az Akadémiai Díjat 1960-ban alapították. A díj az évek során több változáson ment át, de azok magát az érmet nem érintették. A díjat az MTA Elnöksége adományozza évente 11 kiemelkedő tudományos tevékenységet végző kutatónak vagy kutatócsoportnak, az utolsó öt évben elért tudományos eredményük elismerésére.

Forrás: mta.hu

A díj idei matematikus díjazott Matolcsi Máté, a HUN-REN Rényi Alfréd Matematikai Kutatóintézet tudományos tanácsadója, a BME Analízis és Operációkutatás Tanszékének egyetemi tanára. Az indoklás szerint a díjat a Fourier-analízis sokrétű alkalmazásaiban – többek között Fuglede spektrális halmazokra vonatkozó, valamint Erdős egységtávolságot elkerülő halmazokra vonatkozó több évtizedes sejtéseinek a megoldásában – vállalt kiemelkedő szerepének elismeréseként kapta.

Középen a díjazott Matolcsi Máté. (Forrás: Szigeti Tamás, mta.hu)

Matolcsi Máté 2003-ban szerzett PhD fokozatot az Eötvös Loránd Tudományegyetemen, 2015 óta az MTA doktora. Pályafutása során dolgozott a Rényi Intézetben, a Budapesti Műszaki és Gazdaságtudományi Egyetemen, a University of Crete-n, a University of Orleans-on, és az Erwin Schrödinger Intézetben.

Az utóbbi évek tudományos eredményei közül arról a kettőről számolunk be röviden, amelyeket a méltatás is megemlít. Az első Bent Fuglede világhírű dán matematikus régóta vizsgált sejtésével kapcsolatos. Fuglede 1974-ben bevezette a spektrális halmaz fogalmát, és megfogalmazta a sejtést, miszerint egy halmaz pontosan akkor spektrális, ha hézagmentesen parkettázza a teret. Matolcsi és Kolountzakis 2006-ban olyan halmazokat konstruáltak, amelyek parkettáznak, de nem spektrálisak. Ez a negatív eredményük ugyan cáfolta a sejtést, de nem cáfolta a sejtés egy konvex testekre vonatkozó változatát. Végül 2019-ben Nir Levvel közös munkájukban sikerült megmutatniuk, hogy a sejtés ebben a módosított formában igaz. Dolgozatuk az Acta Mathematica-ban, a világ egyik vezető matematikai folyóiratában jelent meg, a szerzők pedig Frontiers of Science Award díjban részesültek.

Matolcsi másik kiemelkedő eredménye Erdős Pál egy sejtéséhez kapcsolódik. Azt mondjuk, hogy egy síkbeli halmaz elkerüli az egységtávolságot, ha bármely két pontja között a távolság nem egyenlő 1-gyel. Erdős 1985-ben azt a sejtést fogalmazta meg, hogy egy ilyen egységtávolságot elkerülő halmaz sűrűsége kisebb, mint 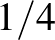$1/4$ . A sejtéssel kapcsolatban az utóbbi évtizedben számos komoly eredmény látott napvilágot, ezek közül több is Matolcsi nevéhez fűződik. A végső áttörést Ambrus Gergely, Csiszárik Adrián, Matolcsi Máté, Varga Dániel, és Zsámboki Pál cikke hozta meg, amelyben a Fourier-analízis, a geometria és a kombinatorika módszereit kombinálták. A cikk a Mathematical Programming című folyóiratban jelent meg 2023-ban.

Az eredményről mi is írtunk az Érintőben.

2. Az MTA III. osztályának díjai

2024. május 8.-án 14:00 órától a Magyar Tudományos Akadémia 197. közgyűléséhez kapcsolódó rendezvénysorozat keretében a Matematikai Tudományok Osztálya „Pozitív definit függvények alkalmazásai” címmel ünnepi délutánt rendezett a Rényi Alfréd Matematikai Kutatóintézetben Nagytermében. Ezen a rendezvényen adta át Páles Zsolt, a Matematikai Tudományok Osztályának elnöke az MTA III. osztályának díjait.

Az MTA Elnöksége 1972-ben – Erdős Pál akadémikus kezdeményezésére és szülei emlékére – a tudományos munkára való ösztönzés és a tudományos utánpótlás támogatása érdekében a matematika és annak ágazatai bármelyikében elért, világviszonylatban is kiemelkedő eredmény elismerésére megalapította a Matematikai Díjat. Erdős Pál halála után a díj nevét az osztály Erdős Pál-díjra változtatta. A díjat évente ítélik oda, az elbírálás előtti három év folyamán elért teljesítményért. Az idei évben a díjat Kiss Gergely kapta a harmonikus analízis, a geometria, a kommutatív algebra, a függvényegyenletek és a félcsoportelmélet vizsgálatában elért eredményei elismeréséül.

Kiss Gergely Erdős Pál-díjas Páles Zsolttal. (Forrás: Nagy Roland, mta.hu)

Kiss Gergely 2015-ben szerzett PhD-t az ELTÉ-n. 2013-2015 között a BME tanársegédje volt, 2015-2018 között posztdoktori állást töltött be a Luxembourgi Egyetemen. 2019-ben az MTA Prémium posztdoktori ösztöndíj elnyerésével tért haza, azóta a Rényi Intézetben dolgozik. Tudományos munkássága rendkívül sokoldalú, foglalkozott harmonikus analízissel, geometriával, kommutatív algebrával, és félcsoportelmélettel is. Ebben a rövid írásban csak egy témát, a diszkrét Pompeiu problémával foglalkozunk.

A diszkrét Pompeiu probléma a 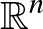$\mathbb{R}^n$ -en a következőképpen formalizálható. Legyen f egy olyan valós (avagy komplex értékű) függvény 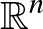$\mathbb{R}^n$ -en, melyre igaz, hogy egy adott véges 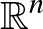$\mathbb{R}^n$ -beli A minta minden, egy adott transzformációcsoport általi képén vett függvényértékeinek összege 0. Igaz-e, hogy az f függvény csakis azonosan 0 lehet? Ha ez az következtetés fennáll, akkor a halmazt Pompeiunak hívjuk az adott traszformációcsoportra nézve. A három legtermészetesebb eset 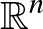$\mathbb{R}^n$ -en az, amikor a szóban forgó transzformációcsoport az eltolások, a hasonlóságok illetve az egybevágóságok csoportja. Kiss Gergely, Laczkovich Miklós, és Vincze Csaba 2018-ban megmutatták, hogy semmilyen legalább 2 elemszámú halmaz nem Pompeiu eltolásokra nézve, illetve 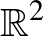$\mathbb{R}^2$ minden részhalmaza Pompeiu a hasonlóságokra nézve. A kérdés egybevágóságokra nézve már a síkon is csak speciális esetben volt ismert. Azonban a közelmúltban egy friss, még nem publikált eredményükben Kiss és Laczkovich megmutatták, hogy 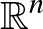$\mathbb{R}^n$ minden véges részhalmaza Pompeiu az egybevágóságokra nézve. Az eredmény jelentősége az is, hogy választ ad Steve Jackson véges Steinhaus-halmazokra vonatkozó alábbi kérdésére: Van-e olyan véges A halmaz a síkon (avagy 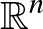$\mathbb{R}^n$ -en), melyhez található olyan S halmaz a síkon (avagy 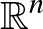$\mathbb{R}^n$ -en), úgy, hogy A minden egybevágó példánya S-sel pontosan egy pontban metsz össze. A fenti eredmények következménye, hogy ilyen halmaz nincsen, ha 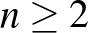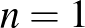$n\ge 2$ . $n=1$ esetben ismert, hogy ilyen véges halmazok léteznek. A teljesség kedvéért megemlítjük, hogy fenti kétszerzős munkában a hasonlóságok esetét kiterjesztették 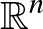$\mathbb{R}^n$ -re tetszőleges 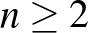$n\ge 2$ esetére, ezzel tisztázva 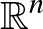$\mathbb{R}^n$ három legtermészetesebb transzformációcsoportjára a Pompeiu problémát.

Alexits György-díjban részesült Virosztek Dániel az optimális transzport elmélete, a kvantum információelmélet, a funkcionálanalízis és a megőrzési problémák vizsgálatában elért eredményeinek elismeréséül. Az 1984-ben alapított díj az Alexits György által elsősorban művelt tudományág, az analízis és annak alkalmazása területén elért kimagasló tudományos eredményekért ítélhető oda.

Virosztek Dániel Alexits György-díjas Páles Zsolttal. (Forrás: Nagy Roland, mta.hu)

Virosztek Dániel 2016-ban szerzett PhD fokozatot a Budapesti Műszaki és Gazdaságtudományi Egyetemen Petz Dénes témavezetésével. Egy évig a BME-n volt posztdoktori állásban, illetve tagja volt a Molnár Lajos által vezetett Funkcionálanalízis Lendület kutatócsoportnak. 2017-től négy éven át a klosterneuburgi IST Austria posztdoktori kutatója volt Erdős László kutatócsoportjában, ebből két évig IST fellowship, két évig pedig Marie Skłodowska-Curie ösztöndíjjal. 2021-ben tért haza az MTA Lendület programjának keretében, azóta a HUN-REN Rényi Alfréd Matematikai Kutatóintézet kutatója.

Első jelentősebb eredményeit témavezetőjével, Petz Dénessel érte el a kvantum információelmélet területén, majd Molnár Lajos hatására figyelme a megőrzési problémák felé fordult. Első közös cikkükben karakterizálták az Einstein giro-csoport folytonos algebrai endomorfizmusait: megmutatták, hogy minden ilyen endomorfizmus a háromdimenziós euklideszi tér egy ortogonális transzformációjából származik. Később Gehér György Pállal és Titkos Tamással egy valószínűségi mértékek tereivel kapcsolatos speciális megőrzési problémát, nevezetesen p-Wasserstein terek izometriáit és izometrikus beágyazásait kezdték vizsgálni. Kiemelkedőek a Transactions of the American Mathematical Society-ban és a Journal of the London Mathematical Society-ben közölt eredményeik, amelyekben a számegyenesre és a kompakt intervallumra épített 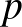$p$ -Wasserstein terek rigiditását vizsgálták. Régóta nyitott kérdés volt, hogy egy teljes szeparábilis metrikus térre épített 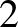$2$ -Wasserstein térnek lehetnek-e tömeghasító izometriái. Virosztek és szerzőtársai megmutatták, hogy ilyen 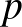$p$ -Wasserstein teret nem csak 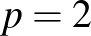$p=2$ , hanem minden 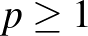$p\geq 1$ -re lehet konsturáulni, ám 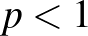$p<1$ esetén ilyen egzotikus 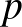$p$ -Wasserstein tér nem létezhet.

Virosztek Dániel jelentős eredményeket ért el a (kvantum) Bregman- és Jensen-divergenciak elméletben is, ezek közül kiemelkedik Lamberti egy több mint tíz éves sejtésének bizonyítása. Az Advances in Mathematicsban közölt cikkben bebizonyította, hogy a kvantum Jensen-Shannon divergencia négyzetgyöke egy valódi metrika a pozitív mátrixok kúpján.

Az MTA 2003-ban a magyar matematika kiemelkedő alakja emlékének méltó megörökítésére Gyires Béla-díj alapítását határozta el. A díjat kétévente ítélik oda a matematikában, elsősorban a Gyires Béla által művelt tudományágak és annak alkalmazásai területén elért kimagasló tudományos eredményekért. A díjat idén Ferenci Tamás kapta a biostatisztikai (orvosi statisztikai) területen, azon belül különösen az orvosi statisztikai kutatások kritikus értékelése terén elért eredményei elismeréséül.

Páles Zsolt átadja a Gyires Béla-díjat Ferenci Tamásnak. (Forrás: Nagy Roland, mta.hu)

Ferenci Tamás 2013-ban szerzett doktori fokozatot az Óbudai Egyetemen, 2019-ben habilitált. Jelenleg az Óbudai Egyetem Élettani Szabályozások Kutatóközpontjának egyetemi docense és a Budapesti Corvinus Egyetem félállású egyetemi docense, emellett óraadó oktató a Semmelweis Egyetem Népegészségtani Intézetében. Tudományos eredményeit 2010-ben Mundruczó György-díjjal, 2013-ban Nyerges Gábor Díjjal, 2017-ben Kemény János-díjjal ismerték el, két alkalommal nyerte el a Markusovszky Lajos-díjat (2017 és 2021), emellett 2011-ben az év fiatal biostatisztikusának választották.

Eredményeit elsősorban biostatisztikai területen, különösen annak epidemiológiával érintkező részein érte el. Munkájának egy jelentős része a HUNVASCDATA projekthez kötődik, melynek keretében kutatótársaival együtt már majdnem egy évtizede vizsgálja a magyarországi érbetegeket és ellátásuk jellemzőit, de számos orvosi terület kutatásaiban működött közre kardiológiától a gyermekgyógyászaton át az infektológiáig. A koronavírus-járvány alatt biostatisztikusaként vett részt a védekezésben, jelenleg is az Egészségbiztonság Nemzeti Laboratórium tagja.

A matematikai területen jelentős az oktatási tevékenysége is, amelynek egy része az utóbbi években már a YouTube-csatornájához kötődik. A tudománynépszerűsítés, ismeretterjesztés területén is aktív, a védőoltásokról írt könyve már két kiadást élt meg, emellett az orvosi kutatások kritikus értékelése kapcsán a szélesebb közvélemény számára írt érvelő, vitatkozó esszéket is rendszeresen publikál (https://www.medstat.hu/).

A Prékopa András-díj a matematikában, elsősorban a Prékopa András által művelt tudományágak: az operációkutatás és az alkalmazott matematika területén elért kimagasló tudományos eredményekért ítélhető oda. Kétévente egy díj kerül átadásra, amelynek odaítélésére javaslatot tehetnek a Matematikai Tudományok Osztálya tagjai és az Osztály Matematikai Tudományos Bizottságának, Operációkutatási Tudományos Bizottságának és az Informatika- és Számítástudományi Tudományos Bizottságának tagjai. A díjat az idei évben Deák István kapta a Monte Carlo-módszerek, véletlenszám-generálási algoritmusok, szimulációs és numerikus módszerek vizsgálatában elért elismeréséül.

Deák István Prékopa András-díjas Páles Zsolttal (Forrás: Nagy Roland, mta.hu)

Deák István az Eötvös Loránd Tudományegyetemen szerzett egyetemi doktori, kandidátusi, majd PhD fokozatot, 2006 óta az MTA Doktora. Pályafutása során dolgozott a BME-n, a SZTAKI-ban, a Nyíregyházi Főiskolán és a Budapesti Corvinus Egyetemen, valamint olyan neves külföldi egyetemeken tanított vendégprofesszorként, mint a kanadai Dalhousie Egyetem, a Wisconsin-Madison Egyetem, a Zürichi Egyetem, és a Rutgers Egyetem. 2014 óta Corvinus Egyetem Professor Emeritusa. Munkásságát korábban Farkas Gyula díjjal (1976) és Egerváry díjjal (2020) ismerték el.

Deák Istvánnak a Monte Carlo-módszerekkel, véletlenszám-generálási algoritmusokkal, szimulációs és numerikus módszerekkel kapcsolatos eredményei között különösen nagy jelentőségűek a többdimenziós normális eloszlás eloszlásfüggvényének kiszámítására kidolgozott eljárása, valamint néhány véletlenszám-generálási algoritmusa. Fontos eredményeket ért el szukcesszív regressziós közelítéseknek a sztochasztikus programozásban való felhasználásával. Új, regresszión alapuló nemlineáris optimalizálási eljárásokat dolgozott ki, amelyek zajos függvények esetén is alkalmazhatók. Eredményeit más elméleti területeken is alkalmazták, ezek között jelentős a térfogatszámítás. Elméleti kutatási tevékenysége több területen is kapcsolódik az alkalmazásokhoz, ipari és gazdasági rendszerek nagyméretű és sztochasztikus optimalizálásával kapcsolatos kérdésekhez.

Információk