A logika szörnyei és a turbulencia

I. Poincaré

„Miért van az, hogy annyi elme nem hajlandó megérteni a matematikát? Nincs ebben valami paradoxon? Hogy lehet az, hogy egy olyan tudomány, amely csak a logika alapelveire, például az ellentmondás elvére hivatkozik, arra, ami úgymond az értelmünk csontváza, arra, amit nem tudunk levetkőzni anélkül, hogy megszűnne a gondolkodásunk, és vannak emberek, akik ezt homályosnak találják! és még ők vannak többségben! Az, hogy képtelenek újat kitalálni, az rendben van, de hogy nem értik a nekik bemutatott demonstrációkat, hogy vakok maradnak, amikor olyan fényt mutatunk nekik, amely számunkra tiszta fénnyel ragyog, az egészen rendkívüli.

Pedig nem kell sok tanári tapasztalat ahhoz, hogy tudjuk, ezek a vak emberek semmiképpen sem kivételesek. Van itt egy probléma, amelyet nem könnyű megoldani, de amelynek foglalkoztatnia kell mindazokat, akik a tanításnak akarják szentelni magukat.”

Ezeket a sorokat Poincaré írta 1908-ban a „Tudomány és módszer” című kötetében. A probléma, amit itt megnevez, a helyes matematikai definíció problémája. Poincaré szerint a jó definíciónak két fontos tulajdonsága kell hogy legyen: le lehessen belőle vezetni matematikai szigorral az objektum kívánt (vagy megfigyelhető) tulajdonságait, de ugyanakkor intuitív legyen hogy egyrészt a tanításnál meg lehessen értetni a dolog lényegét és másrészt hogy ne szüljön szörnyeket. Az, hogy milyen szörnyekre gondol itt Poincaré, azt egy pár oldallal később írja le:

„A logika néha szörnyeket szül. Az elmúlt fél évszázadban rengeteg olyan bizarr függvény megjelenésének lehettünk tanúi, amelyek látszólag arra törekednek, hogy a lehető legkevésbé hasonlítsanak a célt szolgáló, becsületes függvényekre. Nincs többé folytonosság, vagy van folytonosság, de nincs derivált, és így tovább. Ráadásul logikai szempontból ezek a furcsa függvények a legáltalánosabbak; azok, amelyekkel anélkül találkozunk, hogy kerestük volna őket, csak speciális esetként jelennek meg….

A múltban, amikor feltaláltunk egy új függvényt, az valamilyen gyakorlati célt szolgált; ma már direkt azért találjuk fel őket, hogy megkérdőjelezzük apáink gondolkodását, és ez minden, amit valaha is kihozunk belőlük.”

A szörny, amire Poincaré itt hivatkozott, 1872-ben született Karl Weierstrass, a híres berlini professzor egyik előadásán, és így néz ki:

$\displaystyle f(x)=\frac{1}{2}\cos(3\pi x)+\frac{1}{4}\cos(9\pi x)+\frac{1}{8}\cos(27\pi x)+\ldots,$

illetve, általánosabban¹

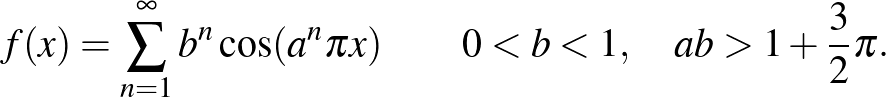
$\displaystyle f(x)=\sum\limits_{n=1}^{\infty}b^n\cos(a^n\pi x)\qquad 0<b<1,\quad ab>1+\frac{3}{2}\pi.$

Ez a függvény, amelyről Weierstrass bebizonyította hogy folytonos, de sehol sem differenciálható, nagy port kavart, főleg az akkori matematika fellegvárában, Párizsban. Ennek két oka volt. Az egyik, hogy akkoriban a differenciál- és integrálszámítás (tehát a valós függvénytan) egyik alaptételének számított a híres francia matematikus és fizikus André-Marie Ampére tétele 1806-ból „théorème fondamental”, amely szerint minden folytonos függvény egy pontosan meghatározható kivételes és izolált halmazon kívül differenciálható („certaines valeurs particulières et isolées”). Ezt sok egyetemi könyvben és jegyzetben megtalálni a 19. században, bár egyes szerzők, pl. Weierstrass, hozzátette gondos előrelátással, hogy a függvény nem csak folytonos hanem szakaszonként monoton legyen. A másik ok bizonyára a francia-porosz háború volt, amelyet a franciák 1871-ben csúfosan elvesztettek. Tehát hogy egy porosz professzor még a francia tételeket is döntögeti, biztos szálka volt a franciák szemében. A híres Charles Hermite, akkoriban a Sorbonne egyetem professzora, a francia akadémia tagja és a francia becsületlégió nagytisztje, 1893-ban egy Stietjes-hez írt levélben ezt írta:

„Az Analízis az egyik kezével elveszi azt, amit a másikkal ad. Elborzadva és megdöbbenve fordulok el a folytonos függvények e siralmas csapásától, amelyeknek nincsenek deriváltjaik…”

Egyszóval nem voltak jó véleménnyel Weierstrass szörnyéről, és hasznát semmiképpen sem látták. Ugyanakkor, mint azt más kontextusból is ismerjük, Poincaré tévedései utólag majdnem hogy fontosabbnak nyilvánultak mint a helyes bizonyításai, és ebben az előadásban erről is van szó.

II. Hidrodinamika

A 20. század elején közismert mondás volt, hogy a hidrodinamikával foglalkozó kutatók társadalma két csoportra osztható: azok, akik a folyadékok olyan tulajdonságait észlelik amiket nem tudunk bizonyítani, és azok, akik a folyadékok olyan tulajdonságait bizonyítják, amiket nem tudunk észlelni. Tehát volt (és bizonyos fokig még mindig van) egyfajta disszonancia a

megfigyelhető, illetve bizonyítható

jelenségek és tulajdonságok között. Erre az egyik kedvenc példám a hidrodinamika egyik nagy klasszikus problémája: Mekkora az ellenálláserő, amely az egyenletes, stacionárius 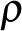$\varrho$ -sűrűségű folyadékban 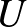sebességgel haladó 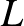sugarú gömbre hat?

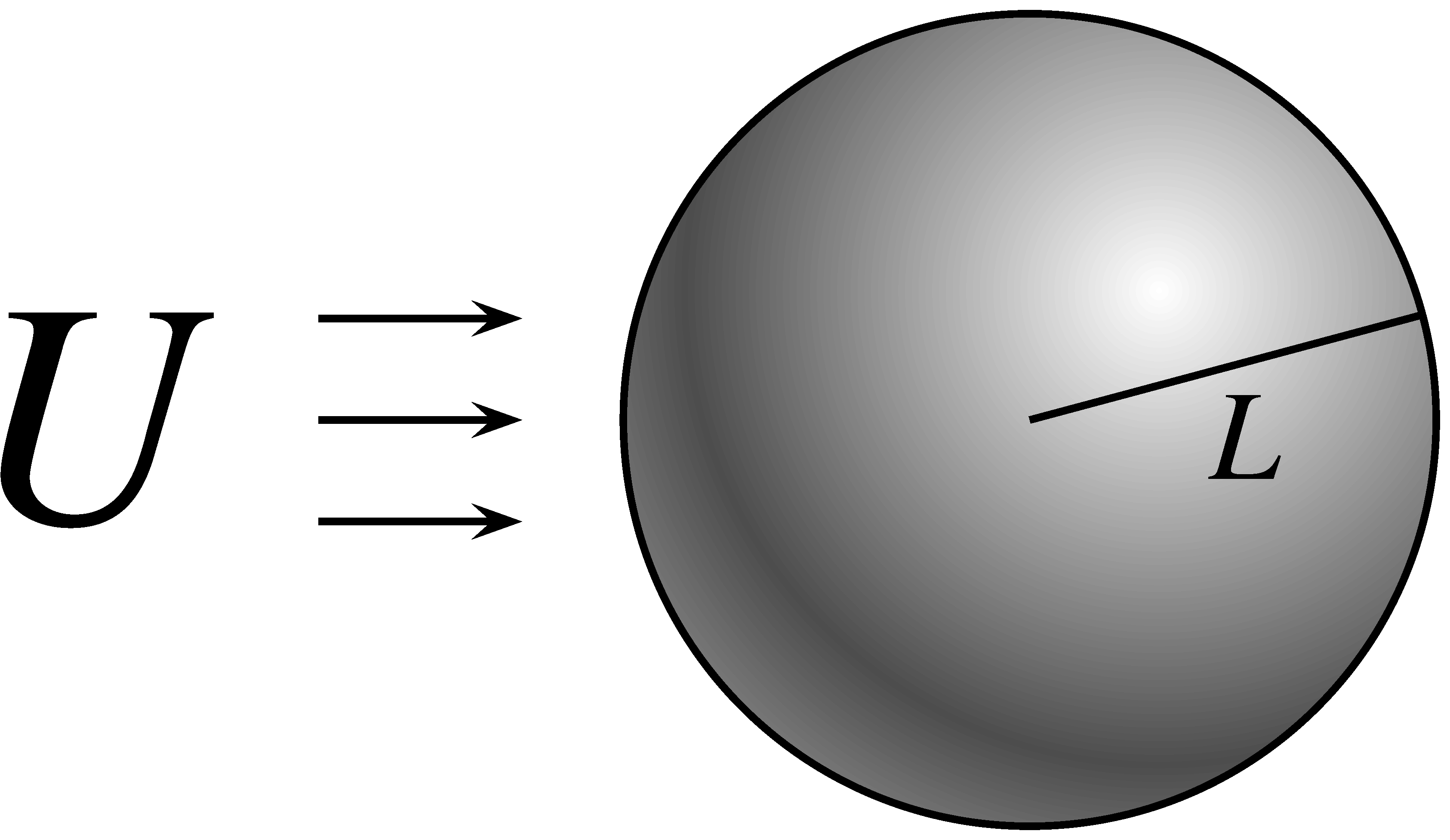
Ezzel már maga Newton foglalkozott, és a Principia-jában megtaláljuk a választ:

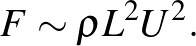
$\displaystyle F\sim \varrho L^2U^2.$

Ezt Newton egyszerűen úgy vezette le, hogy ha feltesszük, hogy 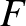$F$ csak ettől a három paramétertől függhet, ez az egyetlen képlet, amelynek helyes a mértékegysége.

Ez a képlet nagyjából megfelel a valóságnak sok esetben, ezt számos kísérlettel lehet igazolni. De mi ezzel a baj? Az, hogy látszólag nem bizonyítható. Ezalatt azt értem, hogy a Newton törvényeket leíró kontinuum egyenletekből, a Navier–Stokes vagy az Euler-egyenletekből nem ez a képlet, hanem valami egész más következik:

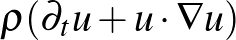$\displaystyle \varrho(\partial_tu+u\cdot\nabla u)$	$\displaystyle =-\nabla p+\nu\Delta u$
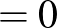$\displaystyle \nabla\cdot u$	$\displaystyle =0$

Amennyiben a folyadék viszkozitása 0, d’Alembert bizonyította 1752-ben, hogy 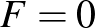$F=0$ . Ez nyilván paradoxon és a valóságnak ellentmond. D’Alembert eredményét Stokes általánosította 1851-ben viszkózus folyadékokra, amely szerint:

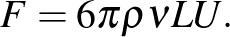
$\displaystyle F=6\pi\varrho\nu LU.$

Stokes képlete is helyes bizonyos esetekben. Hogy Stokes-nak vagy Newtonnak van igaza, az attól függ, hogy mennyire turbulens a folyadék. Ezt egy dimenziómentes mérőszámmal, a Reynolds-számmal szokás kvantifikálni.

$\displaystyle {Re}=\frac{LU}{\nu}.$

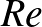Ha ${Re}$ kicsi (kb. 1), akkor Stokes-nak van igaza. Ha 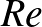${Re}$ nagy (kb. 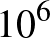$10^6$ ), akkor Newtonnak. A 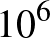$10^6$ soknak tűnik, de ez a tipikus Reynolds-szám pl. egy autónál városi közlekedésnél. Megfigyelhetjük, hogy ha a viszkozitás 0-hoz tart, akkor a Reynolds-szám divergál végtelenhez, tehát egyrészt Newton turbulens esetében vagyunk, másrészt az egyenletrendszer formálisan leegyszerűsödik az Euler-egyenletté, ahol viszont d’Alembert tétele érvényes. Ez a baj.

III. Gyenge megoldások

A kulcskérdés az, hogy mit fogadunk el mint megoldás definíciója, és ehhez tudni kell hogy a

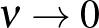
$\displaystyle \nu\to 0$

határátmenet egy szinguláris perturbáció.

Hogy ez mit jelent, azt Michael Berry írta le nagyon találóan:

Ha beleharapunk egy almába, és egy kukacot találunk benne, az elég kellemetlen felfedezés. De ha csak egy fél kukacot találunk, az még rosszabb; ha egy kukac egyharmadát, az még kellemetlenebb. Ugye minél kevesebb hányadát találjuk meg a kukacnak az első harapás után, annál többet ehettünk meg. Ugyanakkor, ha nincs egyáltalán kukac az almában a harapás után, akkor minden oké. Erre mondjuk azt, hogy a „kukachányad tart nullához” határérték szinguláris.

Ugyanez a szituáció áll fenn ha a Navier–Stokes-egyenletnél a viszkozitás nullához tart – illetve a Reynolds-szám tart végtelenhez. A probléma az, hogy az Euler-egyenletnek létezik sima megoldása, de ez a sima megoldás nem írja le a turbulens mozgást, amit a gömb körül, illetve a gömb mögött észlelünk. Tehát meg kell változtatni a megoldásfogalmat, itt jönnek a képbe a gyenge megoldások.

Bár azt hihetnénk, hogy a parciális differenciálegyenletek gyenge megoldáselmélete a huszadik században keletkezett a modern funkcionálanalízis születésével párhuzamosan, de igazából a gyenge megoldások története olyan régi, mint a parciális differenciálegyenleteké. Az első egyenletek egyike a kifeszített húr rezgését leíró lineáris hullámegyenlet,

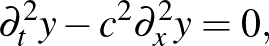
$\displaystyle \partial_t^2y-c^2\partial_x^2y=0,$

amelyet d’Alembert 1747-ben írt fel, és lényegében azt a fizikai tételt írja le, hogy a húrra ható függőleges erő (és ezáltal a gyorsulása) egyenesen arányos a húr görbületével. d’Alembert le is vezette ennek az egyenletnek az általános megoldását,

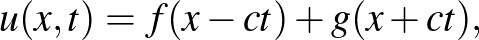
$\displaystyle u(x,t)=f(x-ct)+g(x+ct),$

szóval az általános rezgőmozgás leírható mint két utazóhullám szuperpoziciója, az egyik $c$ sebességgel jobbra, a másik $c$ sebességgel balra tart. Itt egyből felmerült a kérdés, hogy ez a képlet hogyan értelmezhető, ha a két hullámot leíró $f$ és $g$ függvények nem deriválhatóak. d’Alembert ezt a lehetőséget egyszerűen kizárta, mert ugye a hullámegyenletben két deriváltat kell tudni értelmezni, viszont Euler azt állította hogy ebben az esetben is kell tudni értelmezni a megoldást. Kettejük között heves intellektuális vita alakult ki, amely arra összpontosult, hogy hogyan lehet egy tört vonal alakú kezdeti értéknél Newton törvényét értelmezni, hiszen a töréspontnál a görbület, így a húrra ható rugalmassági erő végtelen nagyságú.

A vitának végül 1760-ban Lagrange vetett véget azzal az érvvel, hogy az erőviszonyokat és Newton második törvényét nem pontonként, hanem, mivel egy kontinuum-modellről van szó, infinitezimális intervallumokon kell tudni értelmezni. Tehát a görbületet kis delta-nagyságú intervallumokon kell átlagolni, ez megadja az átlagolt erőt, amely delta-nagyságú intervallumokra hat, és ha az ebből keletkező delta-átlagolt mozgásnak van egyértelmű $\delta\to 0$ limesze, akkor ez a limesz az egyértelmű megoldás.

Ezzel tulajdonképpen Lagrange bevezette a gyenge megoldások elméletét, amit manapság disztribució-értelemben vett megoldásnak nevezünk. A Navier–Stokes-egyenlet esetében a gyenge megoldás exisztenciaelmélete sokkal bonyolultabb, ezt csak 1934-ben sikerült Jean Leray-nek megalkotnia. Mellesleg ezt a megoldásfogalmat Leray „solution turbulent”-nek nevezte.

Van még egy másik definíciója is a gyenge megoldásnak, és ez is a hullámegyenlettel kezdődött. Ha a húr két végét fixáljuk, akkor természetesebb elképzelni a húr mozgását mint sajátrezgések szuperpozicióját, nem pedig utazóhullámok szuperpoziciójaként. Így a Fourier sorfelbontáshoz jutunk, miszerint

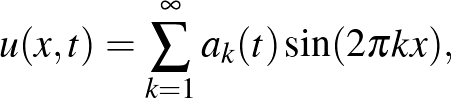
$\displaystyle u(x,t)=\sum\limits_{k=1}^{\infty}a_k(t)\sin(2\pi kx),$

és minden amplitúdó egy közönséges differenciálegyenletet kell hogy megoldjon:

$\displaystyle \frac{d^2}{dt^2}a_k(t)=-4\pi^2c^2k^2a_k(t).$

Ez a megoldás akkor értelmezhető, ha a sor abszolút konvergál, de ebben az esetben a megoldás nem feltétlenül deriválható. Az Euler-egyenletre Lars Onsager alkalmazta ezt a megoldás-definiciót, erre még visszatérünk.

Azt is hozzáteszem, hogy ha más kikötést nem teszünk, ez a két definíciója a gyenge megoldásnak ekvivalens.

Mint említettem, a Navier–Stokes-egyenletre Leray dolgozta ki a gyenge megoldások exisztenciatételét, de unicitást nem tudott bizonyítani. A gyenge megoldások egyértelműsége mai napig megoldatlan probléma. Az Euler-egyenletre sokkal később sikerült gyenge megoldásokat konstruálni, először Vladimir Scheffernek sikerült 1993-ban. Viszont ami itt született, az megint egy szörny (Cedric Villani fogalmazása szerint): Scheffer bizonyította, hogy az Euler-egyenletnek létezik olyan gyenge megoldása, amely egy kezdeti időintervallumban 0, tehát a folyadék sebessége nulla, azután a folyadék egyszer csak el kezd magától mozogni, és egy még későbbi időintervallumban magától a folyadék megint megáll és a sebessége nulla. Nyilván egy olyan megoldásról van szó, ami fizikai szempontból semmiképpen sem értelmezhető. Tehát azzal, hogy a megoldásfogalmat általánosítottuk, átestünk a ló másik oldalára, és az új kérdés az hogy milyen plusz kikötésekkel tudnánk a gyenge megoldások közül a fizikailag értelmezhetőeket kiválasztani.

IV. Energiakaszkád

Ennél a pontnál vizsgáljuk meg újra a Fourier-soros definíciót. A hullámegyenletnél minden sajátrezgés amplitúdója egymástól függetlenül változott, és minden sajátrezgés kinetikus energiája külön-külön időben konstans volt – ezért volt könnyű dolgunk. Viszont a Navier–Stokes és az Euler-egyenlet nem lineáris, a nemlinearitás miatt a különböző sajátrezgések egymással kapcsolatban vannak, és egymásnak átadhatják a kinetikus energiájuk egy részét. Így egy energiakaszkád jön létre, ezt egy egyszerű modellel szeretném illusztrálni.

Képzeljünk el különböző méretű kerekeket, amelyek szabadon tudnak forogni. Ezek a kerekek szimbolizálják a különböző nagyságrendű Fourier-sajátrezgéseket, illetve folyadékáramlás esetében a különböző karakterisztikus méretű folyadékmozgásokat. A hullámegyenlet esetében minden kerék egymástól függetlenül forog, és mindegyiket külön erő forgatja. De a nemlinearitás miatt a Navier–Stokes és Euler-egyenleteknél van kapcsolat, ez itt legyen egy plusz áttétel és lánc, ami a szomszédos kerekeket összeköti. Mint egy bicikli végtelen sok kerékkel, mondhatjuk: Hilbert-bicikli.

Most képzeljünk el egy turbulens áramlást. Az első, amit észreveszünk turbulens áramlásnál, hogy részleteiben kaotikus és megismételhetetlen, de a mozgás statisztikája (pl. egy pontban vett sebesség változásainak disztribuciófüggvénye) időben eltolás-invariáns, más szóval stacionárius. Itt kézenfekvő a statisztikus fizika eszközeit bevetni, de figyelembe kell venni, hogy nem egy zárt rendszerről van szó, mert egy turbulens folyamot állandóan keverni kell, hogy mozgásban maradjon és állandóan kinetikus energiát veszít ugyanolyan arányban a belső súrlódás miatt. Neumann János szavaival élve itt a stacionárius állapotot nem az energia ekviparticiója, hanem a disszipáció ekvipartíciója írja le. Ez ezt meghatározó paraméter tehát az energiadisszipáció mértéke 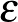$\epsilon$ . A turbulencia egyik empirikus alaptétele (sokan ezt a turbulencia nulladik tételének nevezik) az, hogy az energiadisszipáció mértéke nem függ a Reynolds-számtól (illetve a viszkozitástól).

A Hilbert-biciklin ezt úgy tudjuk modellezni, hogy pedált rakunk az első kerékre, és féket az utolsóra. A kérdés, hogy a 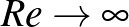${Re}\to\infty$ „turbulens limeszben” a stacionárius állapotban mekkora lesz az egyes kerekek kinetikus energiája. Ha feltesszük, hogy az 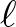$\ell$ -sugarú kerék energiája csak az 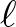$\ell$ hossztól és 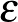$\epsilon$ -tól függhet, ezt kapjuk:

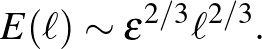
$\displaystyle E(\ell)\sim \epsilon^{2/3}\ell^{2/3}.$

Ez egy variánsa a Kolmogorov-féle $5/3$ tételnek (ami ennek a Fourier-transzformáltja). Mivel a kinetikus energia a sebesség négyzetével arányos, ez egy sebességfüggvénynek felel meg, amely kísértetiesen hasonlít Weierstrass szörnyére:

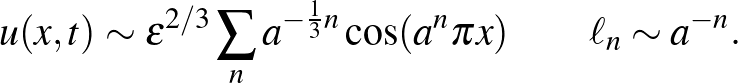
$\displaystyle u(x,t)\sim \epsilon^{2/3}\sum\limits_na^{-\frac{1}{3}n}\cos(a^n\pi x)\qquad \ell_n\sim a^{-n}.$

Mivel a disszipáció mértéke független a viszkozitástól, a 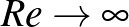${Re}\to\infty$ limeszben olyan gyenge megoldásokat kell keresni az Euler-egyenlethez, amelyeknél az energia nem marad meg, pedig nincs külső erő – mert a fék infinitezimális és nem látni. Olyan ez, mint az infinitezimális kukac az almában. Onsager 1941-ben megfogalmazott sejtése pont erről szól, tehát hogy létezhetnek ilyen struktúrájú gyenge megoldások. Pontosabban, léteznek Hölder-folytonos de nem deriválható sebességfüggvények az 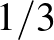$1/3$ exponensig, amelyeknél a kinetikus energia nem állandó, 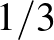$1/3$ exponens felett viszont a kinetikus energia szükségképpen állandó minden gyenge megoldásnál. Ezt kb. 5 éve sikerült igazolnunk.

A tételünknek viszont volt egy szépséghibája: az energia csökkenhet, de nőhet is, és a kettő között csak mesterségesen tudunk különbséget tenni. Ugyanis a módszerünk, a Hilbert-biciklin illusztrálva, a következő. Nem az első kerékre rakjuk a pedált, hanem a másodikra. Persze, mivel ez a kerék kisebb, ugyanakkor kinetikus energia generálásához gyorsabban kell tekerni. Ha a harmadikra rakjuk a pedált, akkor még gyorsabban és így tovább. Ad infinitum azt kapjuk, hogy az infinitezimálisan kis pedált tekerjük végtelen sebességgel, vagyis mintha Maxwell démonja tekerné Hilbert bicikliét.

És nemcsak tekerni hanem kontrázni is tud, persze. Ezt az egyszerű konstrukciós elvet Gromov konvex integrálás módszerével sikerült megvalósítanunk, de persze ez a Scheffer-féle szörnyekhez is vezetett.

V. A nulladik törvény

Egy turbulens áramlásnál, ha átlagolunk kis 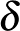$\delta$ -méretű tartományokon, akkor meg kellene kapnunk egy nagyobb, effektív viszkozitást, ami azon a skálán megfelel a disszipáció mértékének – ugyanúgy, ahogy Lagrange átlagolása megadta az effektív rugalmassági erőt a kifeszített húr kis 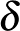$\delta$ -szakaszain. Ennek a matematikai módszere a homogenizálás. Egy tavaly ősszel megjelent cikkben a lipcsei kollegáimmal sikerült együtt alkalmaznunk a homogenizálást a konvex integrációval: bár még nem a Navier–Stokes-egyenletre, hanem a lineáris transzport-diffúzió egyenletre:

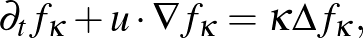
$\displaystyle \partial_tf_{\kappa}+u\cdot\nabla f_{\kappa}=\kappa\Delta f_{\kappa},$

ahol az 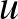$u$ vektormező az Euler-egyenlet Onsager-féle gyenge megoldása. Ez az egyenlet azt írja le, hogy hogyan változik pl. egy, a turbulens áramlásba befecskendezett, anyag sűrűsége 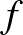$f$ , ha ez egyrészt az áramlással együtt sodródik (transzport), másrészt kis kappa diffúziós együtthatóval terjed. A tételünk azt mondja ki, hogy az effektív diffúzió mértéke független a kappától:

$\displaystyle \limsup\limits_{\kappa\to 0}\frac{\int\bigl\vert f_{\kappa}(x,t)\... ...t^2\,\mathrm{d}x}{\int\bigl\vert f_{\kappa}(x,0)\bigr\vert^2\,\mathrm{d}x}<1.$

Itt a négyzetintegrál nem más mint az 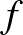$f$ sűrűség szórása. Enyhén túlzással ez egy matematikai bizonyítása a turbulencia nulladik törvényére, legalábbis a passzív transzport speciális esetében.

VI. Pillangóhatás

Visszatérve a Scheffer-szörnyhöz, most szeretnék arra rámutatni, hogy ez a Scheffer-szörny, tehát a Maxwell-démon által hajtott Hilbert-bicikli, mégis hasznos kapcsolatban van valós jelenségekkel, de nem a hagyományos, Kolmogorov-féle energiakaszkáddal kapcsolatban, hanem egy úgynevezett inverz-energiakaszkáddal kapcsolatban. Ehhez kicsit ki kell térnem a Lorenz-féle pillangóhatásra.

Ennek a közismert változata, amely Edward Lorenz 1963-as cikkére van alapozva, azt jelenti, hogy véges dimenziós kaotikus dinamikus rendszereknél a apró (de véges) változtatása a kezdeti feltételeknek nagy változásokat okoz a későbbi dinamikában: „egy pillangó egyetlen szárnycsapása a Föld egyik oldalán tornádót idézhet elő a másikon”. Most én egy sokkal komolyabb pillangóhatásról szeretnék beszélni, ami Edward Lorenz kevésbé ismert 1969-es cikkére alapul. Itt nem alacsony-dimenziós dinamikus rendszerekről van szó, mint a klasszikus értelemben (az eredeti Lorenz-rendszer háromdimenziós), hanem magas-dimenziós rendszerekről.

Lorenz ebben a cikkben bevezette a kiszámíthatósági tartomány, illetve kiszámíthatósági idő fogalmát. Ez alatt egy olyan időintervallumot kell érteni, amelyen belül, ha tipikus nagyságú mérési hibákat végzünk a kezdeti állapot meghatározásánál, akkor ez még elfogadható nagyságú hibát eredményez. Tehát ennyi ideig még egy elfogadható hibahatáron belül maradunk. A kiszámíthatósági idő nyilván arányos lesz egy adott skálán adott kinetikus energiával rendelkező dinamikus rendszer tipikus időskálájával, tehát

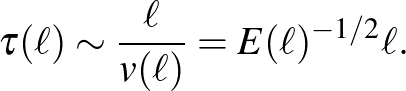
$\displaystyle \tau(\ell)\sim\frac{\ell}{v(\ell)}=E(\ell)^{-1/2}\ell.$

Vegyünk most egy olyan dinamikus rendszert, amely nagy szabadsági fokszámmal rendelkezik, tehát sok különböző skálán történik a dinamika – ilyen a föld alsó atmoszférájában a levegő áramlása. Tegyük fel azt is, hogy a dinamika nemlineáris, és minden skálán vett mozgás előbb-utóbb instabillá válik, ezután pedig lényegesen hat nagyobb skálákon is. Tehát pl. 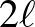az $\ell$ skálán vett mozgás $\tau(\ell)$ idő után instabillá válik és hatással lesz a $2\ell$ skálán történő dinamikára. Ebben az esetben azt kérdezhetjük, hogy egy, kis 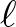$\ell$ skálán vett hiba mennyi idő múlva van lényeges hatással a nagy 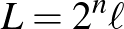$L=2^n\ell$ skálán történő dinamikára? A válasz nagyon egyszerű:

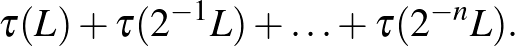
$\displaystyle \tau(L)+\tau(2^{-1}L)+\ldots+\tau(2^{-n}L).$

Lorenz rámutatott, hogy két lehetséges szituáció létezik, attól függően, hogy a

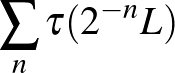
$\displaystyle \sum\limits_n\tau(2^{-n}L)$

sor konvergál-e vagy sem. Ha konvergál, az azt jelenti, hogy bármilyen kis skálán vett hiba fix véges időn belül (ami arányos a $\tau(L)$ idővel) lényegesen befolyásolja a dinamikát. Ez a pillangóhatás erős változata! Ha viszont divergál, akkor minél kisebb skálán történik hiba, annál tovább tart, mire az a hiba látszani fog a nagy skálán. Ugyanez megfogalmazva a kiszámíthatósági idővel: ha a sor konvergál, akkor a rendszer kiszámíthatósági ideje felülről korlátos, bármilyen precíz méréseket is végzünk.

Mint láttuk, a Navier–Stokes turbulens áramlásában

$\displaystyle E(\ell)\sim^{\ell^{2/3}}\quad \tau(\ell)\sim \ell^{2/3},$

tehát a fenti sor konvergál. Ha ezt a föld alsó atmoszféráján vett áramlásra alkalmazzuk, akkor a következő megdöbbentő eredményt kapjuk: ha mondjuk az 1000 km-es skálán vett kiszámíthatósági idő 3 nap (tipikus számok az európai meteorológiai előrejelzésnél), akkor a hasonlósági elv miatt az 1 km-es skálán vett kiszámíthatósági idő kb. 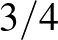$3/4$ óra (ez pl. egy tipikus felhő mérete) és 1 m-es skálán vett kiszámíthatósági idő kb. fél perc. Tehát, ha sok pénzből elhatároznánk, hogy a meteorológiai előrejelzéshez a numerikus felbontást és az ehhez szolgáltatott mérési adathálózatot (amely jelenleg kb. 5–10 km felbontású) 1 m-es felbontásra finomítjuk, akkor ezzel a kiszámíthatósági időt, tehát az időt, amelyen belül a mérési és numerikus hibahatár elfogadható marad, csak kb. fél perccel javítanánk!

Persze nagyobb távolságokon (pl. nagyobb mint 10 km) a tipikus atmoszferikus dinamikát nem a 3D Navier–Stokes-egyenlet írja le, hanem 2D egyenletek, pl. a kvázi-geosztrófikus egyenlet (amely hasonlít a 2D Euler-egyenlethez) – az első numerikus időjárás-előrejelzésnél, amelyet Neumann János vezetésével végeztek a princetoni Institute for Advanced Study-ban 1950-ben, ezt az egyenletet használták. Ennél az egyenletnél az energiaspektrum más, itt

$\displaystyle E(\ell)\sim\ell^2\qquad \tau(\ell)\sim 1,$

tehát itt Lorenz jobbik esetében vagyunk, ahol a sor divergál.

Tisztán matematikai szemszögből nézve Lorenz gondolatmenete azzal áll kapcsolatban, hogy a kezdetiérték-problémának létezik-e egyértelmű megoldása. Ehhez pedig nem feltétlenül a stacionárius állapot energiaspektruma mérvadó, hanem a kezdeti sebességmezőé. Itt egy érdekes példa a 2D Euler-egyenletnél fellépő Kelvin–Helmholtz instabilitás, amelynél a kezdeti sebességmező nem folytonos hanem van egy szakadása, ebből pedig következik hogy a kezdeti energiaspektrum nem a fenti, hanem

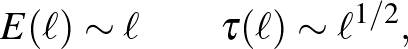
$\displaystyle E(\ell)\sim\ell\qquad\tau(\ell)\sim\ell^{1/2},$

és ismét a konvergáló esetnél vagyunk. Azt ugyan nem nehéz igazolni, hogy ebben a speciális esetben végtelen sok gyenge megoldás létezik, viszont a kérdés megint az, hogy melyik megoldás-definíció szerint? Ugyanis ennél a végtelen sok gyenge megoldásnál (úgy mint a Scheffer-féle szörnynél) a sebességmező „csak” egy $L2$ függvény, tehát mérhető, és a négyzete integrálható, viszont a Kelvin–Helmholtz kezdeti sebességmező vorticitása egy véges mérték (ez majdnem azzal ekvivalens hogy a sebességmező korlátos változású), és azt tudjuk (ez Jean Delort francia matematikus híres cikke 1992-ből), hogy létezik olyan gyenge megoldás, amelynek ez a tulajdonsága megmarad. Továbbá, ez az a megoldástípus, amit akkor kapunk ha a sima megoldások terét lezárjuk, vagyis klasszikus megoldások limeszeit vesszük.

A matematikai probléma tehát az, hogy tudjuk-e igazolni a Lorenz-féle erős pillangóhatást a Kelvin–Helmholtz instabilitásra, tehát azt, hogy ha a kezdeti sebesség a Kelvin–Helmholtz-nak tetszőlegesen közeli sima approximációja, akkor egységnyi idő alatt a Kelvin–Helmholtz stacionárius megoldástól, lényeges, egységnyi eltérést tapasztalunk. De ez már a jövő muzsikája.

ifj. Székelyhidi László

A Kelvin-Helmholtz instabilitás hatására kialakuló spirális örvények:

https://www.idojarasesradar.hu/idojaras-info/hullamzo-egbolt-ritka-fotok-kelvin-helmholtz-felhok--52f69d0e-cff3-4402-ae7e-a4f1b11271c1

Lábjegyzet

: ¹Aki figyel a részletekre, észre fogja venni hogy a fenti példa nem teljesíti Weierstrass kikötését az 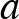és 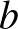paraméterekre. Viszont 1916-ban Hardy bizonyította, hogy elégséges az 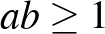$ab\ge 1$ feltétel is.