Az Erdős–Moser sejtés bizonyítása

A sík legfeljebb mekkora hányada színezhető ki úgy, hogy két kiszínezett pont nem lehet pontosan egység távolságra egymástól? Ezt a geometriai kérdést Leo Moser fogalmazta meg az 1960-as évek elején, Hadwiger és Nelson egy rokon problémájával kapcsolatban. Leo Moser és Erdős Pál sejtése szerint ez a hányad nem érheti el az 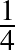$\frac{1}{4}$ -et; a jelenleg ismert legerősebb, 0,2293 értékű alsó korlátot Hallard Croft 1967-es konstrukciója adja. A problémával kapcsolatban számos kutatócsoport publikált már részeredményeket, amelyek a kezdeti 0,2857-es felső sűrűség-becslést az elmúlt 60 évben fokozatosan 0.2544-ig élesítették. Az Ambrus Gergely (Szegedi Tudományegyetem és Rényi Intézet), Csiszárik Adrián (Rényi Intézet és Eötvös Loránd Tudományegyetem), Matolcsi Máté (Budapesti Műszaki Egyetem és Rényi Intézet), Varga Dániel (Rényi Intézet) és Zsámboki Pál (Rényi Intézet) által jegyzett új eredményünk szerint a kérdéses sűrűség nem haladhatja meg a 0,247-et. Ezzel sikerüt igazolnunk Leo Moser és Erdős Pál sejtését [2].

Egységtávolság-kerülő halmaznak nevezzük azon ponthalmazokat, amelyeknek semelyik két eleme nincs egység távolságra egymástól. Moser kérdése tehát a sík mérhető, egységtávolság-kerülő halmazainak lehetséges legnagyobb felső sűrűségére vonatkozik – az általánosság megszorítása nélkül az is feltehető, hogy a kérdéses halmaz sűrűsége létezik, ami ekkor intuitíve a halmaz által fedett síkrész arányát jelenti. Bár a kérdés természetesen értelmezhető, és aktívan kutatott a térben, gömbfelszínen és további struktúrákon is, mi a továbbiakbakban kizárólag a klasszikus, síkbeli változatra szorítkozunk. Ebben az esetben a feltétel úgy is megfogalmazható, hogy ha egy pont benne van az egységtávolság-kerülő halmazban, akkor a köré rajzolt egység sugarú körvonal nem metszheti a halmazt.

Minél nagyobb sűrűségű egységtávolság-kerülő halmazokat keresve természetesen adódik a következő konstrukció: egy egység átmérőjű nyílt körlemez egységtávolság-kerülő, hiszen az összes, két pontja között előforduló távolság kisebb 1-nél. Az ezzel egybevágó nyílt körlemezeket pedig úgy helyezhetjük el egységtávolság-kerülő módon a leggazdaságosabban, hogy egy 2 lépésközű szabályos háromszögrács pontjai köré írjuk őket. Ezzel két különböző körlemez tetszőleges pontjai közötti távolság szigorúan 1-nél nagyobb lesz.

Az így konstruált halmaz sűrűsége nagyjából 0,2267. Ezt sikerült Hallard Croftnak 1967-ben megjavítania közel 0,2293-re. Croft nem változtatta meg túlságosan a konstrukció logikáját, de rájött, hogy érdemes a körlemezeket egy kicsit sűrűbben elrendezni, még azon az áron is, hogy emiatt egy kis részt le kell vágni belőlük az egységtávolság-kerülő tulajdonság megtartásához. Az így adódó, egy körlemez és egy gondosan megválasztott oldalhosszú szabályos hatszög metszeteként előálló halmazt Croft teknősének hívja a szakirodalom (ld. 1. ábra).

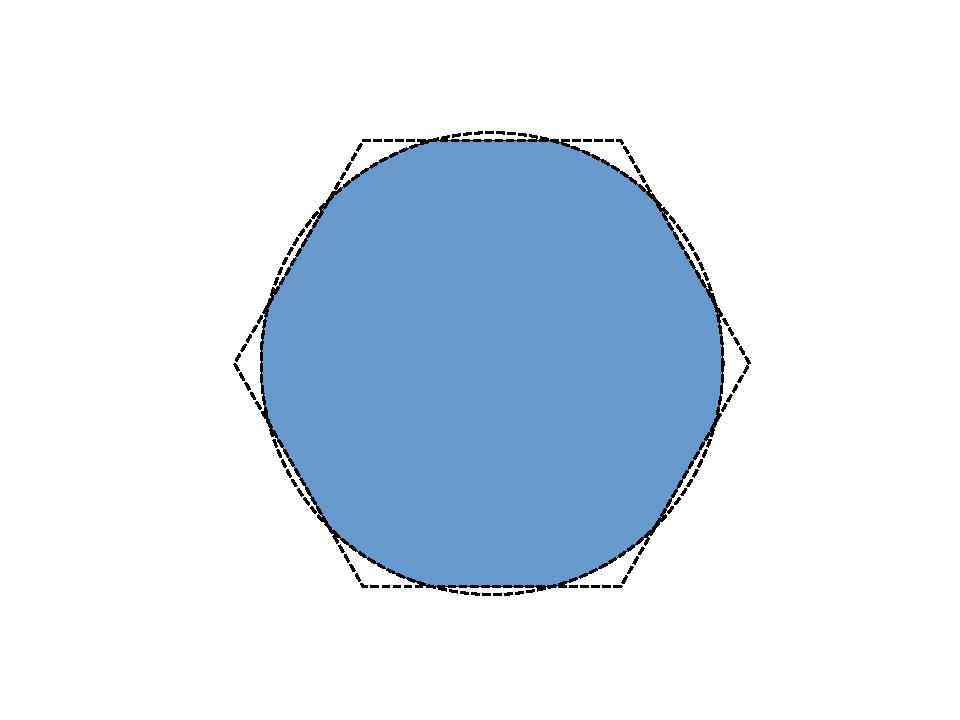
1. ábra. Croft teknőse

Bár Croft konstrukciója kissé esetlegesnek tűnhet, és 1967 óta számosan próbálkoztak jobbat találni nála, ez máig sikertelen maradt. Ma már sokan azt sejtik, hogy a konstrukció a lehető legnagyobb sűrűségű egységtávolság-kerülő halmaz a síkon. Érdekes tulajdonsága, hogy 4 diszjunkt példány is elhelyezhető belőle a síkon.

Hogyan bizonyíthatjuk, hogy egy egységtávolság-kerülő halmaz (amit jelöljünk mostantól 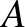$A$ -val) nem lehet nagy sűrűségű? Logikus gondolat a következő: toljuk el az 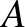$A$ halmazt 1 távolságra valamilyen irányba, az eltolt halmaz természetesen 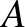$A$ -val azonos sűrűségű. Jelöljük 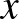$x$ -szel az eltoláshoz használt egységvektort, és 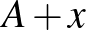$A+x$ -szel az eltolt halmazt. 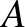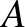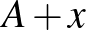Mivel $A$ nem tartalmaz két, egységnyi távolságra levő pontot, így $A$ és $A+x$ metszete szükségképpen üres. Innen pedig rögtön adódik, hogy az 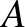$A$ halmaz sűrűsége legfeljebb 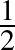$\frac{1}{2}$ . A gondolatot továbbvezetve, egy (tetszőlegesen elhelyezett) egység oldalú szabályos háromszög csúcsainak helyvektorát választva az eltolásokhoz, a három kapott eltolt példány páronként diszjunkt, ami 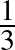$\frac{1}{3}$ felső becslést ad az 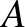$A$ halmaz sűrűségére.

2. ábra. Egy egységtávolság-kerülő halmazból lerakható három, páronként diszjunkt eltolt példány, tehát sűrűsége nem lehet nagyobb, mint 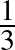$\frac{1}{3}$ .

A felső becslések sorát folytatta Leo Moser 1966-ban a 3. ábrán látható, Moser-rokkának nevezett gráf segítségével, amelynek élei 1 hosszúságúak.

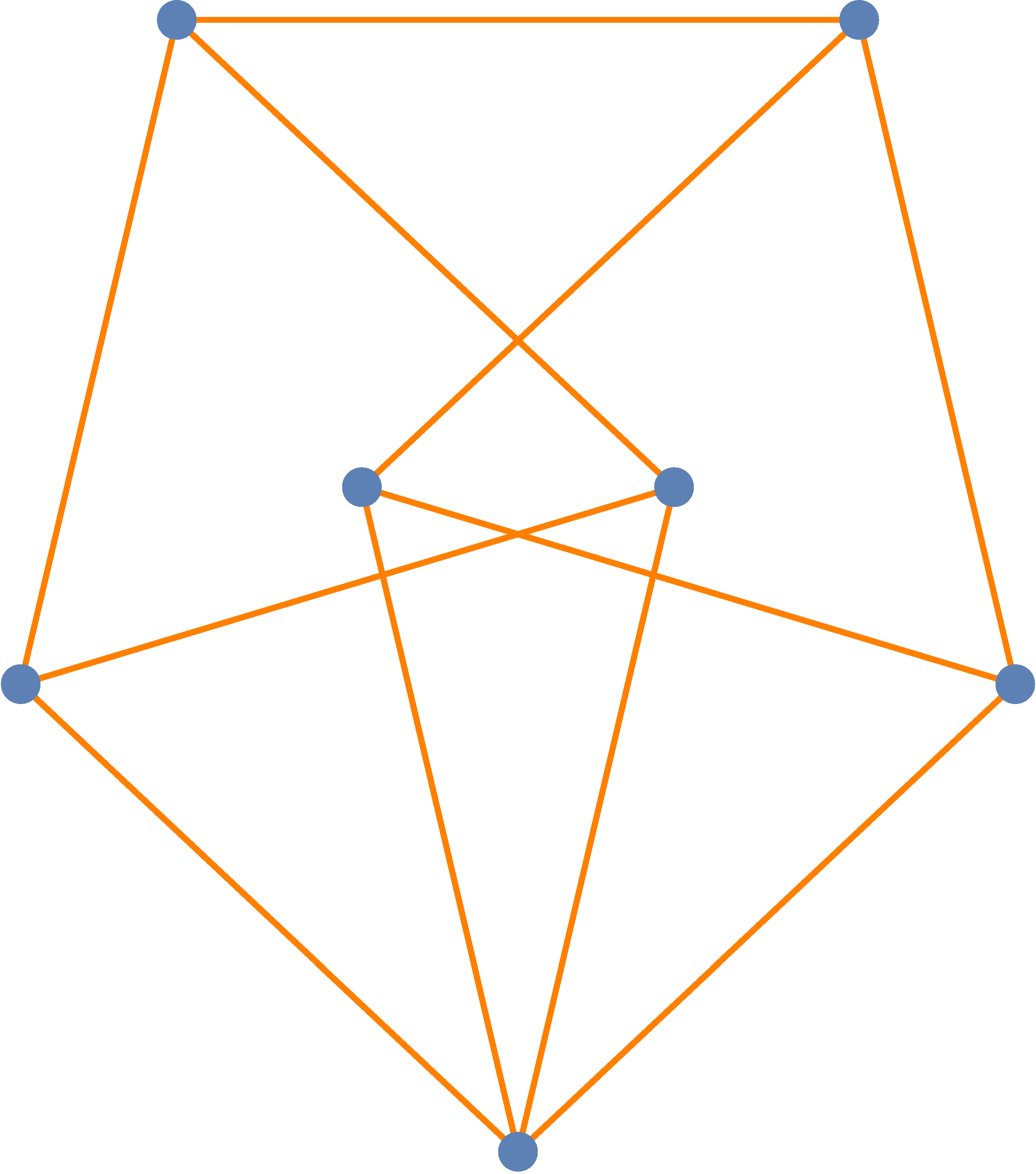
3. ábra. Moser rokkája

Könnyen ellenőrizhető, hogy a gráf függetlenségi száma 2, így akárhogy is választjuk ki három csúcsát, azok között lesz legalább egy él. Ebből pedig rögtön következik, hogy ha az 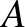$A$ halmazt a gráf csúcsainak helyvektoraival toljuk el, akkor az így kapott 7 egybevágó, eltolt példány legfeljebb 2 rétegben fedi le a síkot (4. ábra), és így 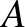$A$ sűrűsége legfeljebb 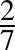$\frac{2}{7}$ lehet.

4. ábra. Egy egységtávolság-kerülő halmazból lerakható 7 eltolt példány úgy, hogy együttesen legfeljebb kétrétűen fedik le a síkot.

Moser eredménye nyomán sokan próbáltak az egységtávolság-kerülő halmazok sűrűségére felső becslést adni hasonló módszerrel: ha sikerül olyan 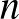$n$ elemű ponthalmazt konstruálnunk, amelynek bármely 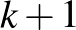$k+1$ eleme között előfordul egységtávolság, akkor beláttuk, hogy tetszőleges 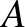$A$ egységtávolság-kerülő halmaz sűrűsége legfeljebb 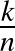$\frac{k}{n}$ , mert az 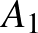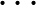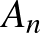$A_1$ , $\dots$ , $A_n$ egybevágó eltolt példányok a sík egyetlen pontját sem fedhetik le 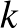$k$ -nál több rétegben. Az évek alatt a hasonló, gráfelméleti módszeren alapuló becslések egyre javultak, Moser 1966-os 0,2857 eredményétől egészen Bellitto, Pêcher és Sédillot 2018-as 0,2565-es felső korlátjáig. Az utóbbi eredmények már komoly számítógépes apparátust használtak a megfelelő ponthalmaz megtalálásához, illetve elvárt tulajdonságainak formális ellenőrzéséhez.

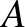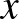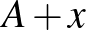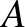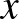Mindeközben F. Vallentin és F. M. de Oliveira Filho munkája nyomán egy másik megközelítés segítségével is egyre erősebb korlátokat sikerült bizonyítani. Emlékezzünk rá, hogy ha $A$ -t egy $x$ síkbeli egységvektorral toljuk el, akkor a kapott $A+x$ halmaz diszjunkt $A$ -tól, tehát az $A\cap(A +x)$ halmaz sűrűsége 0. Természetes ötlet elhagyni az $x$ vektor egységnyi hosszára vonatkozó feltételt. Így a kérdéses sűrűséget 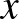$x$ függvényeként definiálhatjuk: ez az úgynevezett autokorrelációs függvény, amelynek formális definíciója

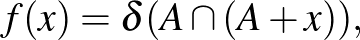
$\displaystyle f(x)=\delta(A\cap(A+x)),$

ahol 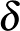$\delta$ a sűrűséget jelöli.

Az autokorrelációs függvény rengeteg információt hordoz magáról az 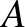$A$ halmazról. Legegyszerűbb példaként vegyük észre, hogy 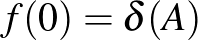$f(0)=\delta(A)$ , míg az egységtávolság-kerülő tulajdonság következményeként 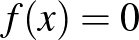$f(x)=0$ minden 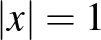$\vert x\vert=1$ esetén. Ez azonban még csak a jéghegy csúcsa, hiszen a függvény segítségével több, különböző vektorokkal vett eltolt metszési struktúrájáról is fontos becsléseket nyerhetünk.

Ezen a ponton szükséges egy alapvető, ám az általános eredményt nem befolyásoló feltevést tennünk: nevezetesen, hogy az 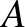$A$ halmaz periodikus (ezt úgy képzelhetjük el, hogy 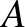$A$ -nak csak egy hatalmas négyzetbe eső részét vesszük, majd a sík többi részén a halmazt ennek négyzetrács-szerű eltoltjaival definiáljuk). E feltétel mellett definiálhatjuk az 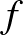$f$ autokorrelációs függvény Fourier-transzformáltját, ami az 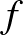$f$ -et elemi trigonometrikus függvények lineáris kombinációjaként építi fel. A harmonikus analízis egy alapvető azonossága, a Parseval-formula pedig garantálja azt, hogy a vonatkozó Fourier-együtthatók nemnegatívak – azaz 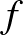$f$ pozitív szemidefinit. Ennek a tulajdonságnak fontos szerep jut majd a későbbiekben.

Visszatérve Moser 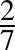$\frac{2}{7}$ -es becslésének bizonyításához, láttuk, hogy a gondolatmenetben az 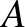$A$ halmaz eltolt példányainak metszési struktúrája játszotta a főszerepet (nevezetesen, semelyik 3 eltoltnak nem lehet közös metszete). Innen természetes általánosítással adódik a következő ötlet: vegyünk egy tetszőleges 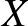$X$ ponthalmazt, ennek elemeivel vett eltoltakat vizsgáljunk, és ezek metszet-sűrűségeinek segítségével próbáljuk optimalizálni a teljes sűrűség-becslést! A kérdéses mennyiségeket az 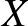$X$ által definiált atomoknak fogjuk hívni: ha 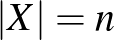$\vert X\vert=n$ , akkor az 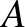$A$ halmaz 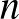$n$ eltoltját véve, az ezeket leíró teljes absztrakt Venn-diagram 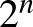$2^n$ cellájának sűrűségei adják optimalizálási problémánk 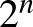$2^n$ atomi változóját.

Az atomok és a Fourier-együtthatók közötti összefüggést azonnal láthatjuk, ha az autokorrelációs függvény értékeit egyszerű, két csúcsú gráfokhoz tartozó atomokként interpretáljuk. Így nemnegatív, atomi és Fourier-változók hadát kapjuk, amelyek között lineáris egyenlőségek, illetve egyenlőtlenségek írhatók fel, többek között a szita-formula megfelelő alkalmazásainak segítségével. Ezeket összegyűjtve végül egy olyan feladathoz jutunk, amelyet matematikai optimalizálás központi eszköze, a lineáris programozás segítségével tudunk kezelni. Kulcsfontosságú, hogy míg a Fourier-változók függetlenek a 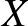$X$ ponthalmaz választásától, addig az atomi változók és a vonatkozó lineáris összefüggések az adott 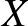$X$ által kerülnek definiálásra, és a kapott rendszer teljesül tetszőleges egységtávolság-kerülő 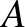$A$ halmazra. Így különböző 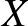$X$ halmazok választásával más és más sűrűségbecsléseket kaphatunk – feladatunk, hogy olyan halmazt keressünk, amelynek segítségével 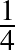$\frac{1}{4}$ -nél kisebb felső becslés adódik.

A fenti módszerre építve, 2022-ben megjelent cikkükben Ambrus és Matolcsi az addigi legerősebb, 0,2544 becslést bizonyították, de az Erdős által sejtett 0,25-os korlát elérése továbbra is távolinak tűnt.

A sejtés bizonyításához szükséges első áttörést az hozta, hogy kutatócsoportunk a korábbinál sokkal teljesebben és általánosabban alkalmazta a gráfelméleti, atomi változókra alapuló megközelítést, illetve ötvözte azt a harmonikus analízis módszereivel. Ennek köszönhetően a problémát egy, a korábbinál jóval összetettebb lineáris programozási feladatra sikerült visszavezetnünk, amit nagy teljesítményű számítógépek segítségével hatékonyan tudtunk kezelni.

Az elméleti háttér pontos kidolgozása után már „csupán” egy megfelelő 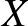$X$ ponthalmaz megtalálására volt szükség. Ahhoz, hogy a kapott becslés minél erősebb legyen, elengedhetetlen, hogy 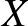$X$ pontjai között sok egységtávolság forduljon elő, valamint hogy 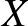$X$ sok egybevágó részhalmaz-párt tartalmazzon. Célunk egy olyan ponthalmaz keresése volt, mely által generált lineáris programozási feladat megoldása szigorúan 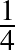$\frac{1}{4}$ alatt van, implikálva az Erdős–Moser sejtést.

A ponthalmaz keresési problémája elemi eszközökkel megoldhatatlannak bizonyult, így a mesterséges intelligencia módszereit alkalmaztuk. Ehhez a Rényi Intézet nagy számítási kapacitású számítógépeit vettük igénybe, amelyeket a Mesterséges Intelligencia Nemzeti Laboratórium (MILAB) biztosított. Több hónapnyi intenzív kísérletezést és algoritmus-optimalizálást követően a számítógép-hálózat végül egy egy hetes keresés során talált olyan 23 pontból álló ponthalmazt, amely alkalmas volt a sejtés bizonyítására (5. ábra).

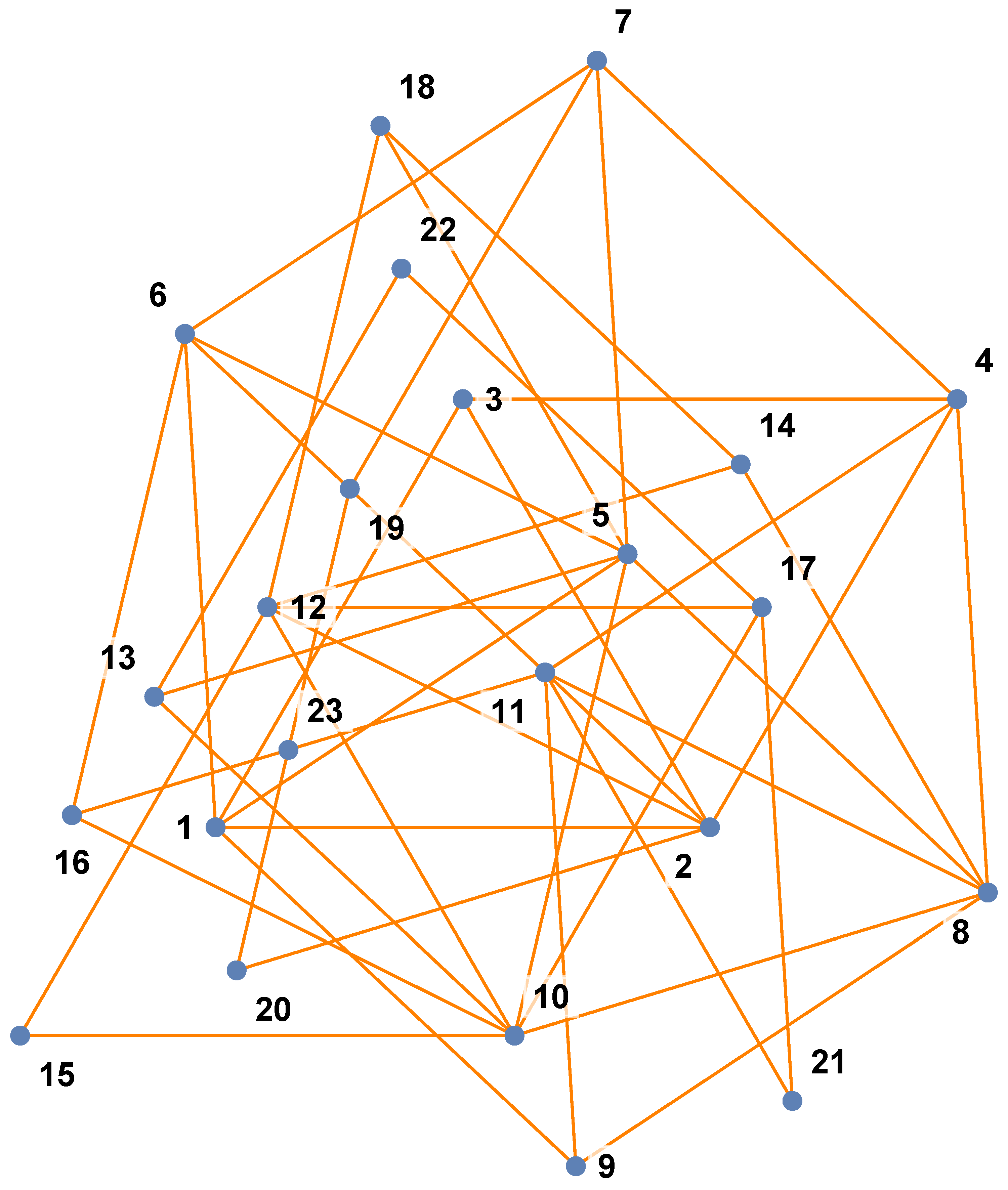
5. ábra. A számítógépes keresés által megtalált 23 elemű ponthalmaz, amely tanúsítványként szolgál arra, hogy Erdős sejtése igaz.

A megfelelő ponthalmaz megtalálása után az Erdős–Moser sejtés igazolásához szükséges utolsó lépés a lineáris programozás dualitására épülő, tisztán elméleti bizonyítás kidolgozása volt, amit a numerikus analízis szokásos eszközeinek alkalmazásával végeztünk el. A végső, tisztán matematikai eszközökkel bizonyított becslés szerint tetszőleges mérhető, egységtávolság-mentes síkbeli halmaz felső sűrűsége legfeljebb 0,247 lehet.

Az eredmény a Mathematical Programming folyóiratban jelenik meg. Az intézmények (Rényi Intézet, BME, ELTE, SZTE), illetve tudományterületek (geometria, Fourier-analízis, lineáris programozás, gráfelmélet, mesterséges intelligencia) közötti sikeres együttműködést a továbbiakban is folytatjuk, célunk a sík színezéseihez kapcsolódó további problémák vizsgálata.