A sonkásszendvics-probléma

Ahogy már egy korábbi Érintő cikkben is szerepelt, a híres lvivi Skót Kávéház olyan kiváló lengyel matematikusok gyülekezőhelye volt, mint Banach, Borsuk, Mazur, Kuratowski, Steinhaus, vagy épp Ulam. Egyes elmondások szerint Banach felesége, mások szerint maga Banach vásárolt egy keményfedeles füzetet, amelybe a fontosabb matematikai problémákat feljegyezték. A füzet, amelynek első oldalán a Ksiega Szkocka, azaz Skót Könyv név szerepel, mindig a kávéházban volt elrejtve, a főpincértől lehetett elkérni, ha szükség volt rá. A könyvben 193 számozott probléma szerepel, az első bejegyzés dátuma 1935. július 17., az utolsóé 1941. május 31. Ebben a cikkben Hugo Steinhaus 123-as sorszámú problémájáról lesz szó, amelyet ma már csak sonkásszendvics-problémaként emlegetnek.

1. ábra. Steinhaus eredeti bejegyzése.

1. A sonkásszendvics-probléma

A probléma (kicsit leegyszerűsítve) így szól: adott három véges térfogatú halmaz 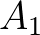, , 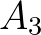a 3-dimenziós Euklidészi térben. Létezik olyan sík, amelyik mindhárom halmazt elfelezi? Steinhaus híres volt arról, hogy a legabsztraktabb problémákat is el tudta magyarázni egy szemléletes példa segítségével. Most sincs ez másképp, noha a konkrét részletek az évek során (ahogy a probléma terjedt) egy kicsit megváltoztak. 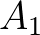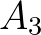A mai verzió így szól: legyen egy szelet kenyér, egy szelet sonka, pedig egy szelet sajt, a felező sík szerepét pedig játssza egy nagyon éles kés.

2. ábra.

Igaz-e, hogy bárhogy is állítanak össze egy sonkás szendvicset ebből a három összetevőből, azt ketté tudjuk vágni igazságosan egyetlen vágással? Igazságos alatt azt kell érteni, hogy a kenyér mennyisége a két fél szendvicsben egyenlő, és ugyanez igaz a sonkára és a sajtra is. Az eredeti probléma kitér a magasabb dimenziós esetre is, mi ebben a cikkben csak a 3-dimenziós kérdéssel, és annak történetével foglalkozunk. Azt már tudjuk, hogy a problémát Steinhaus tűzte ki. A Skót Könyv egy későbbi (egyébként üres) oldalán egy megjegyzést találunk, ugyancsak Steinhaustól: a megoldás megtalálható a Mathesis Polska 1936-os számában.

3. ábra. Addendum a 123-as problémához.

Bár a Skót Könyv létezéséről sokan tudhattak akkoriban, az nem valószínű, hogy mindenki naprakész volt a benne található problémákat illetően, az pedig egészen biztos, hogy Lengyelországon kívül nem sokan olvasták a lengyel nyelven írt Mathesis Polskát. Nem meglepő, hogy a sonkásszendvics-probléma eredetét illetően volt némi zavar. Stone és Tukey 1942-es [5] cikkében az áll, hogy a fent bemutatott probléma (pontosabban ahogy ők hívják: tétel) bizonyítása Karol Borsuk egy tételén alapul, és lábjegyzetben hozzáteszik, hogy a felfedezés Stanisław Ulamtól származik. Ezenfelül köszönik a bírálónak, hogy felhívta a figyelmüket erre a tényre. Borsuk és Ulam neve, mint az rögtön kiderül, nem véletlenül került szóba.

Steinhaus a náci megszállás alatt (egészen a második világháború végéig) egy Osiczyna nevű településen bujkált, egy nem sokkal korábban elhunyt erdész, bizonyos Grzegorz Krochmalny iratait használva. Amikor a háború végeztével megtudta, hogy a lvivi egyetemet „átköltöztették” Wroclawba, ő maga is elfogadott ott egy állást. Egy 1945-ös cikkében [4] – amelyben a bujkálás évei alatt kidolozott eredményeket közöl – bebizonyítja a sonkásszendvics-tételt, és megjegyzi, hogy a probléma tőle származik, és elsőként Stefan Banach oldotta meg, Borsuk és Ulam tételét felhasználva. Mielőtt rátérnénk a matematikára, néhány mondat Borsukról és Ulamról.

4. ábra. Karol Borsuk (balra) és Stanisław Ulam (jobbra).

[Fotók: Wikimedia Commons illetve https://www.researchgate.net/figure/Polish-mathematician-Stanislaw-Ulam-together-with-the-current-version-of-the-first-page_fig5_229066089 uploaded by Francesc Font-Clos]

Stanisław Ulam a lvivi matematikai iskola kiemelkedő alakja, számtalan mély matematikai eredmény fűződik a nevéhez. Legtöbben mégis fizikusként ismerik, ugyanis részt vett a termonukleáris fegyverek kifejlesztésére szolgáló Manhattan-tervben. Ulam szerepe a Skót Könyv történetében is rendkívül jelentős: egyrészt ő maga is tűzött ki és oldott meg problémákat, másrészt ő volt az, aki – a világháborút egy futballpályán elásva átvészelő – Skót Könyvet angolra fordította. A fordítás 1957-ben Los Alamosban jelent meg.

Karol Borsuk a varsói matematikai iskola jeles képviselője, nevéhez köthető a topologikus terek elméletének több fontos eredménye. A német megszállás alatt kivette a részét az ellenállásból, többek között folytatta az akkoriban tiltott egyetemi szintű tanítást. Emiatt a Gestapo börtönbe zárta, és csak a szerencsének köszönhette, hogy elkerülte a kivégzést [2]. Egy érdekesség: a börtönből szabadulva, hogy családját valahogy eltartsa, kifejlesztett (és saját költségén ki is adott) egy társasjátékot, amit ma Szuper Farmer néven forgalmaznak. Sokáig úgy hitték, hogy a varsói felkelés és a háború utáni káoszban az összes eredeti példány megsemmisült, de később találtak egy sértetlen készletet, és Borsuk 90. születésnapja és halálának 15. évfordulója alkalmából a játékot újra kiadták.

5. ábra. A társasjáték magyar kiadása.

2. A bizonyítás (vázlata)

Térjünk rá a bizonyításra, pontosabban annak egy vázlatára. Vázlatról beszélünk, mert formálisan nem lesz kifogástalan (arról nem is beszélve, hogy két segédtételt nem bizonyítunk), de a valóban precíz bizonyítás is ezeket a lépéseket követi, lásd például [1,3,4]. Az [1] cikk már csak azért is érdekes, mert abban le van írva, hogy a szerzők hogyan jutottak hozzá az addendumban említett Mathesis Polska számhoz, és közlik a sonkásszendvics-tételről szóló rész angol fordítását.

Egy egyszerűbb problémával kezdünk, nevezetesen egy síkbeli alakzat, egy képzeletben kétdimenziós pizza elfelezésével. A hétköznapi életben hogyan feleznénk el nagyjából igazságosan egy pizzát? Valahová odaillesztenénk a késünket, és megnéznénk, hogy azzal a vágással feleznénk-e. Ha úgy látjuk, hogy a késtől balra lévő rész nagyobb, akkor kicsit balra mozdítjuk a kést. Ha úgy látjuk, hogy most meg már a jobboldali rész nagyobb, akkor az igazság valahol a két vágás között van. Lényegében itt is ezt fogjuk tenni.

Rögzítsünk egy 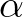szöget, ez az a szög, amiben a kést tartjuk.

6. ábra.  A pizza és az 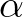szögben álló kés.

Csúsztassuk végig az 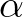szögben tartott kést a pizza fölött.

7. ábra.  Az 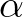szögű vágások.

A csúsztatás során minden időpillanatban feljegyezzük, hogy mennyi a kés két oldalán lévő területek különbsége (a jobboldali darabból levonva a baloldalit). Az alábbi ábrán két kimerevített pillanat (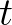 és ) látható. Ha az adott pillanatban vágnánk, akkor a pizza 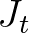és területű, illetve 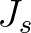és területű darabokra esne.

8. ábra. Vágás a 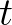és pillanatokban.

Azt látjuk, hogy a területek különbsége egyszer negatív, egyszer pedig pozitív, következésképp valahol a két kimerevített pillanat között volt olyan is, amikor a különbség nulla volt, tehát a kés két oldalán lévő terület megegyezett.

Miről van itt szó? Először is, a késünket folytonosan mozgatjuk, tehát ha csak egy kicsit mozdítjuk meg, akkor a vágásnál kapott területek nagysága is csak kicsit változik. Tehát a területek eltéréséből készített függvény folytonos, így a negatív és pozitív érték között valahol nullát is fel kell vegyen, ezt Bolzano tételének nevezik.

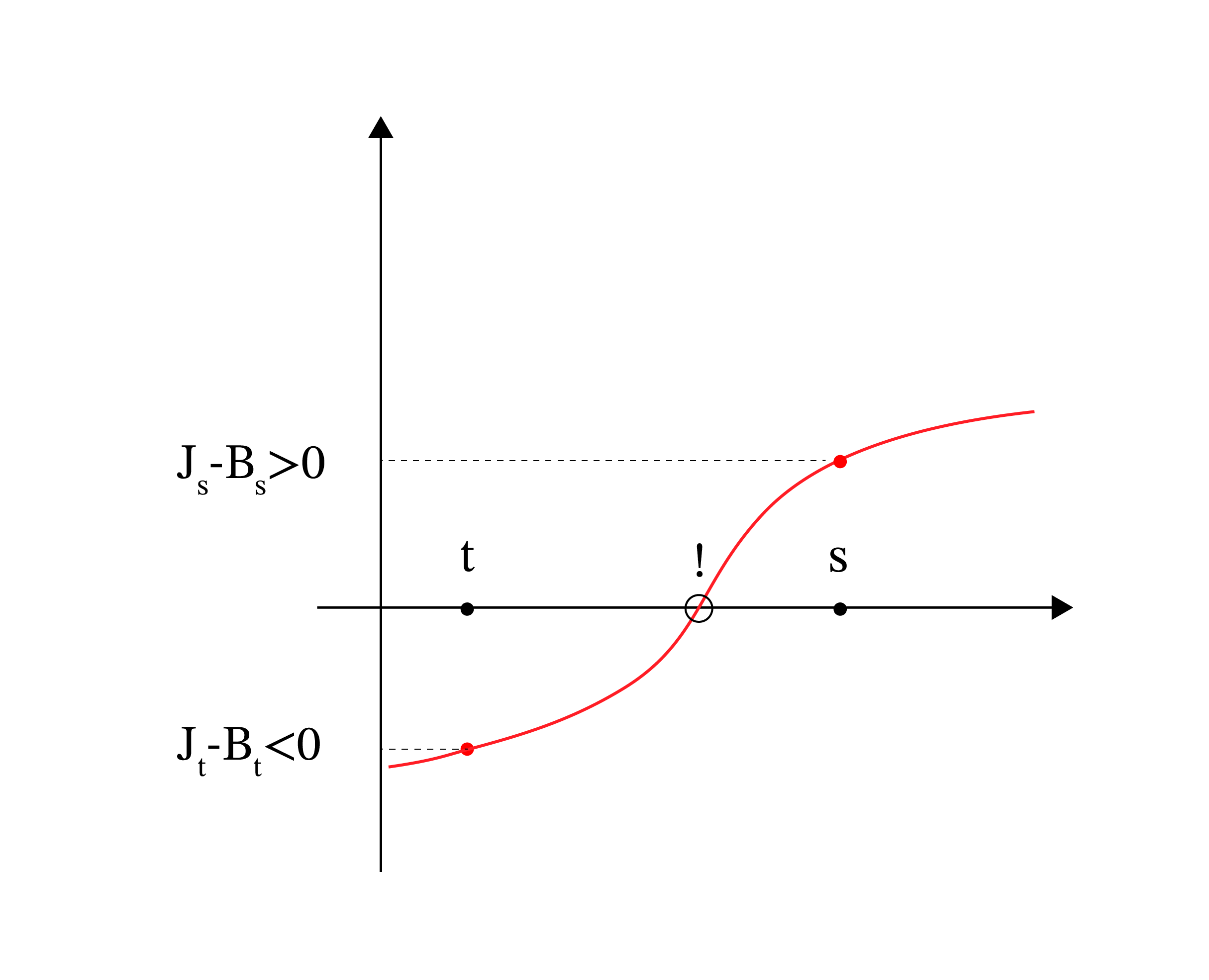
9. ábra. Szemléletesen: ha egy határ egyik oldaláról átjutottunk a határ másik oldalára, akkor valahol átmentünk a határon.

Másodszor, teszünk egy egyszerű megfigyelést, ami később jól fog jönni. Tegyük fel most, hogy nem a vágás során kapott területek különbségét jegyezzük fel, hanem mindig csak a késtől jobbra levő rész területét. Igen ám, de ha átmegyünk a pizza túloldalára, és „szemből vágunk” (azaz 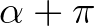szögben vágunk), akkor megfordulnak az oldalak, és a 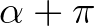vágásnál az a rész van jobbra, amelyik az 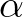-vágásnál balra volt. Tehát ha az 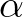és a 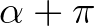szögű vágásoknál ugyanazt a mennyiséget jegyeztük fel, akkor az épp azt jelenti, hogy a pizzánkat megfeleztük.

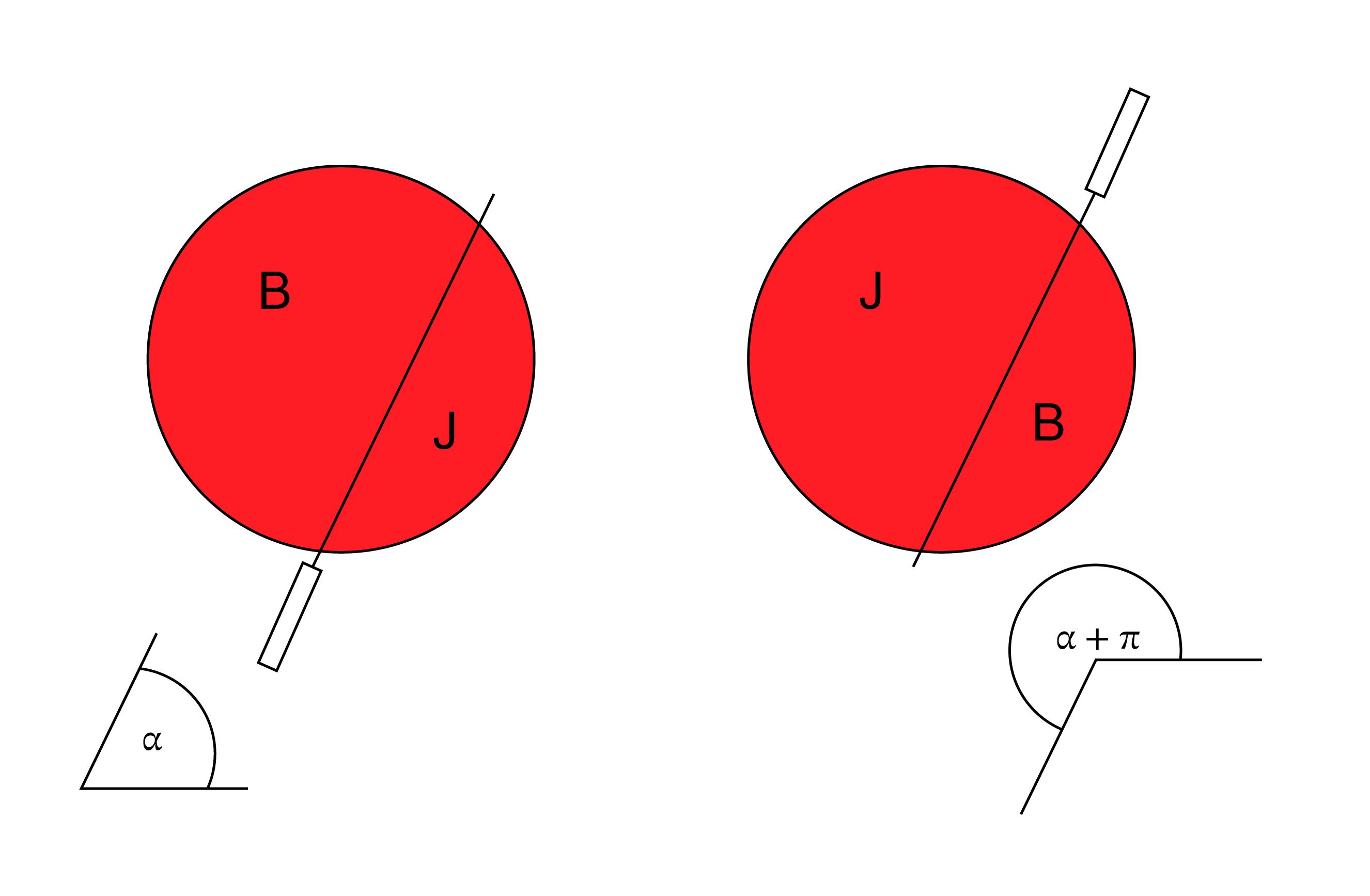
10. ábra. A bal oldal és a jobb oldal szerepet cserél.

Vegyük észre, hogy a fenti csúsztatós okoskodásunkban nem játszott semmilyen szerepet, hogy az 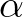szöget milyennek választottuk: minden szöghöz pontosan ugyanígy találunk egy felező vágást. Sőt, valójában a pizza alakja sem volt érdekes, sőt még a dimenziója sem. Ha a síknak feltételezett pizza helyett most egy valódi háromdimenziós sajtdarabra gondolunk, amit félbe kell vágnunk egy síkkal, akkor ugyanezt az elvet követjük: fogunk egy tetszőleges síkot, elkezdjük folytonosan csúsztatni a sajt mentén, és vágunk abban a pillanatban, amikor a sík két oldalán lévő részek térfogatának eltérése nulla. Ilyen időpillanat létezik, megintcsak a Bolzano-tétel miatt.

Tehát most ott tartunk, hogy egy darab halmazt a háromdimenziós térben már el tudunk felezni bármilyen dőlésszögű sík segítségével. Mielőtt tovább mennénk, próbáljuk meg ügyesen elképzelni az összes lehetséges dőlésszögű síkot. Vegyünk a háromdimenziós térben egy gömbfelületet, jelölje ezt . Ezekután az gömbfelület minden pontjához képzeljük oda a gömböt abban a pontban érintő síkot.

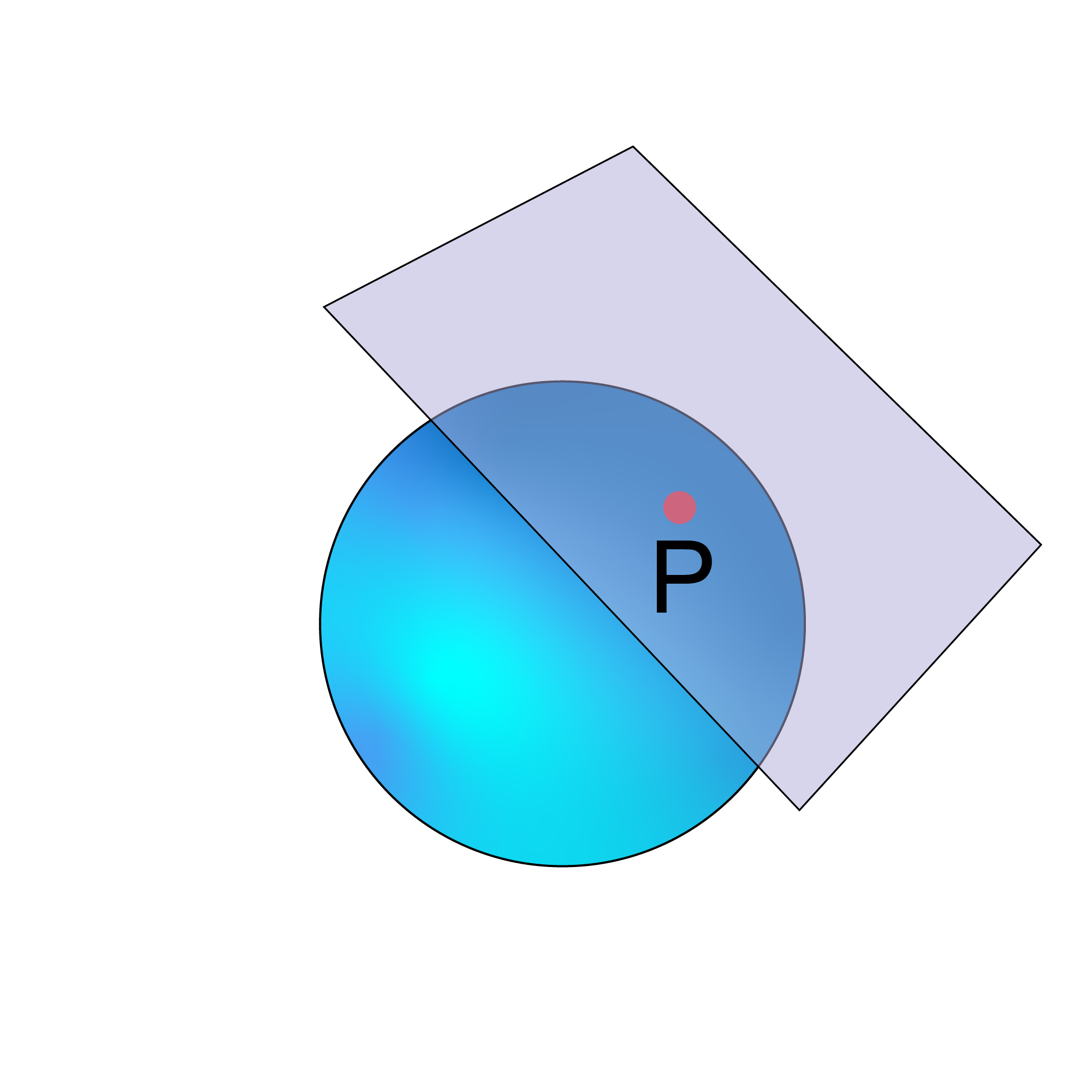
11. ábra. A gömbfelület 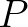pontja, és a 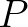-beli érintősík.

Az így kapott (síkokból álló) kollekció valóban minden létező dőlésszögű síkot tartalmaz, ráadásul kétszer. Érdemes már most megjegyezni, hogy 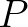-hez és a 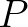-vel szemközti 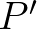ponthoz ugyanolyan dőlésszögű sík tartozik.

12. ábra. A 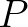-beli és 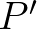-beli érintősíkok egymás eltoltjai.

Ne feledjük, hogy a feladatunk három halmaz együttes felezése, mi pedig eddig csak egyet tudunk elfelezni, igaz azt sokféleképp. Mi garantálja, hogy van ezek között olyan felezősík, ami a másik két halmazt is felezi? Ezen a ponton kell használnunk Borsuk és Ulam tételét. A tétel azt mondja, hogy ha 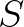pontjait folytonosan beleképezzük a síkba, akkor lesz olyan 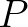pont, hogy a függvény értéke 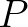-ben és a vele átellenes 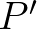-ben megegyezik. Ismét csak Steinhaus szemléltető képességeire támaszkodva ezt így lehet közérthetően elmondani: képzeljük el, hogy 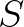a Föld bolygó felszíne. A Föld minden 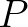pontjában feljegyzünk két értéket: a hőmérsékletet (jelölje ezt 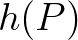) és a nyomást (jelölje ezt 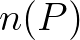). Ezzel az 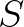minden pontját beleképeztük a síkba: a 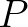ponthoz hozzárendeltük a 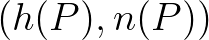hőmérséklet–nyomás számpárt. Mit mond a tétel? A tétel azt mondja, hogy ha egy időpillanatban elvégezzük a két mérést a Föld összes pontján, akkor mindig találni fogunk egy olyan 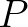pontot, hogy 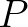-ben és a vele átellenes 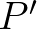pontban 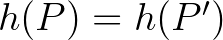és 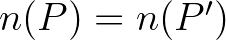, azaz mindkét pontban ugyanannyi lesz a hőmérséklet és a nyomás is. A szemléletető példában maga a hőmérséklet és a nyomás semmilyen szerepet nem játszott, nyugodtan képzelhetünk (és képzelni is fogunk!) a helyükbe bármilyen mérhető mennyiséget. A Borsuk–Ulam tételt itt nem igazoljuk. Az érdeklődő olvasó az [1] cikkben talál egy ravasz bizonyítást, ami Auerbachtól származik.

A fenti előkészületek után minden készen áll ahhoz, hogy bebizonyítsuk a sonkásszendvics-tételt. Adott tehát három halmaz, 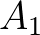, és .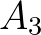. Azt már tudjuk az előző okoskodásból, hogy az 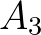-at el tudjuk felezni egy síkkal, ráadásul nagyon sokféleképpen. A gömbfelület minden pontjához tartozik egy sík, ahhoz pedig egy felezés. Vegyük az 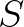gömbfelületünknek egy 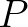pontját, és vegyük az érintősíkot, ami 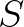-et 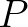-ben érinti. Ennek a síknak két oldala van, nevezzük az 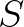-et tartalmazó részt a negatív oldalának, a másikat pedig a pozitív oldalának. Értelemszerűen, ha a síkot eltoljuk, akkor vele együtt mozog a pozitív és negatív oldala. (Ahogy az eltolásnál együtt mozgott a késsel a bal és a jobb oldala. Vigyázzunk, a kés forgatásánál már helyet cserélt a két oldal!) Tudjuk, hogy ennek a síknak valamelyik eltoltja pont félbevágja 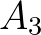-at. Jegyezzük fel, hogy 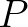-hez melyik felezősíkot választottuk, és hogy ez a sík hogyan metszette 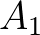-et és -t. Konkrétabban: jegyezzük fel, hogy az 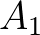-nek mekkora területű része van az 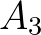-at felező sík pozitív oldalán (jelöljük ezt a számot 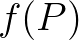-vel), és hogy -nek mekkora része van az 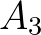-at felező sík pozitív oldalán (jelöljük 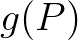-vel). Tehát a gömb 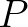pontjához feljegyeztünk egy 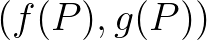párt.

13. ábra. Az 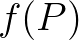szám a zöld ellipszoid sík fölötti részének térfogata, a 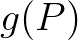szám a lila ellipszoid sík fölötti részének térfogata.

Azt is megbeszéltük, hogy az átellenes 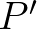ponthoz ugyanolyan dőlésszögű sík tartozik, mint 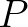-hez, tehát 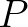-hez és 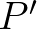-höz választhatjuk ugyanazt az 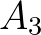-at elfelező síkot. Az egyetlen különbség, hogy pozitív és negatív oldalak 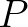és 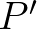esetén pont fordítva vannak, hiszen a gömb ezeknek a síkoknak „ellentétes oldalán” van. (Úgy is képzelhetjük, mintha a fenti ábrát kézenállva néznénk, és ami az előbb alul volt, az így felülre kerül.) Emlékezzünk vissza, ugyanezt láttuk a pizzás példánál a „túloldali vágásnál”! Ott a bal és jobb oldal cserélt helyet, itt pedig az pozitív és negatív oldal. Hasonlóan az ott leírtakhoz, itt is azt látjuk, hogy 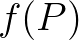és 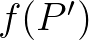együtt épp az 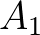félbevágásáról ad információt, 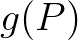és pedig az félbevágásáról.

Ahhoz, hogy mindhárom halmazt jól vágjuk félbe, az kell, hogy találjunk egy 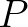pontot, amire 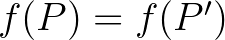és 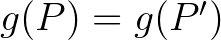egyszerre teljesül, magyarul 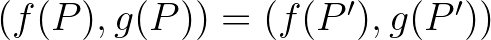. Borsuk és Ulam fenti tétele épp azt mondja, hogy ilyen pont biztosan létezik.

Ezzel a bizonyítás kész. Tehát ha két ember között igazságosan kell elfeleznünk egy sonkás szendvicset (bármilyen slendrián módon is van elkészítve, bárhogy is néz ki a három összetevő, bárhol is helyezkednek el a térben), biztosak lehetünk benne, hogy létezik olyan vágás, ami megoldja a problémánkat. Mivel két olyan tételt is használtunk, nevezetesen a Bolzano-tételt és a Borsuk–Ulam-tételt, ami csak létezést garantál, ezért arról természetesen fogalmunk sincs, hogy pontosan melyik lehet az a bizonyos igazságos vágás.

A legjobb módszer a lehető legnagyobb pontosság elérésére valószínűleg az, ha az egyik ember vág, és a másik választ.

Irodalomjegyzék

[1] W. A. Beyer, A. Zardecki, The Early History of the Ham Sandwich Theorem, The American Mathematical Monthly, 111:1 (2004), 58–61.

[2] A. Granas, J. Jaworowski, Reminiscences of Karol Borsuk, Topol. Methods Nonlinear Anal., 1993, 3–8.

[3] H. Steinhaus and others, Notatki: Z topologii, Mathesis Polska, XI, (1938), pp. 26–28.

[4] H. Steinhaus, Sur la division des ensembles de l'espace par les plans et des ensembles plans par les cercles, Fundamenta Mathematicae, Volume: 33, Issue: 1 (1945), 245–263.

[5] A. H. Stone, J. W. Tukey, Generalized “sandwich” theorems, Duke Mathematical Journal, 9 (1942) (2): 356–359.