A XX. századi matematika egyik rendkívül érdekes fejezete a Lvivben található Skót Kávéházhoz köthető. Ugyan Lviv ma Ukrajnához tartozik, történetünk kezdetén, 1935-ben a lengyel-szovjet háborút lezáró rigai béke értelmében Lwów néven még Lengyelország részét képezte. A Skót Kávéház matematikusaira ezért mint lengyel matematikusokra szokás hivatkozni. 1939-től aztán szovjet fennhatóság alá került a város egészen az 1941-es német megszállásig. Azon túl, hogy az Einsatzkommando azonnal megölt több mint 45 professzort (köztük három matematikust: Antoni Marian Lomnickit, Stanislaw Ruziewiczet, és Wlodzimierz Stożeket), a németek a népes zsidó lakosságot, köztük jónéhány matematikust gettóba gyűjtötték, koncentrációs táborokba deportálták, vagy épp orvosi kísérleteknek vetették alá. Noha nyilvánvaló, hogy a város tragédiákkal terhelt történelme és a Skót Kávéház tudósainak élete nem választható szét, ebben a most induló cikk- és bejegyzéssorozatban megpróbálunk főleg a matematikára és a társaság környezetének sokszínűségére fókuszálni.
1. A Skót Kávéház
A huszadik század első felében a kávéházak a társasági élet legfontosabb helyszínei voltak Európa-szerte: irodalmárok, képzőművészek, tudósok csoportjai tartottak rendszeres összejöveteleket, vagy éppen dolgoztak egy-egy kávéház törzsvendégeként. Példaként említhetjük Karinthy Frigyest, aki amellett, hogy előszeretettel írt kávéházakban, és vélhetően a szórakoz(tat)ásra is szakított némi időt, a Hadikban működő sakk-kör elnöki posztját is betöltötte. (Egyik leghirhedtebb sakk eredménye, hogy egy szimultán alkalmával komiszul ellopta a világbajnok Alekszandr Aljechin egyik bástyáját.) De említhetnénk a Japán kávéházat is. Faludy György elmondása alapján: „A Japán a XX. század első évtizedeiben a főváros egyik neves kávéháza volt, elsősorban festők találkozóhelye. A tulajdonos szerette volna, ha kávéházát költők is látogatják – ez vonzerőt gyakorolt a polgári közönségre –, de a kávé árát kevesen tudtuk volna megfizetni. Ezért létesítette az úgynevezett mocsár asztalt. Ide pincér csak akkor jött, ha kifejezetten hívták, viszont óránként 2-2 pohár friss vizet tett mindenki elé tálcán. Borravalót értünk a tulajdonos adott, nehogy a pincérek lenézzenek bennünket.”
Lwówban a Monopol és a Café de la Paix voltak az „irodalmi kávéházak”, míg a fizikusok, kémikusok és matematikusok törzshelye az egyetemhez közeli Róma Kávéház volt.
Tomasz Broda lengyel művész formabontó képein (http://www.matematyka.wroc.pl/
Íme az eredeti fényképek, Banach és Steinhaus:
Heti rendszerességű szemináriumuk után ide vonult át a Stefan Banach és Hugo Steinhaus nevével fémjelzett Lengyel Matematikai Társaság tagsága kiegészülve néhány kiváló fiatal hallgatóval, köztük Stanislaw Ulammal. (Ulam neve főleg az termonukleáris fegyverek kifejlesztésére szolgáló Manhattan-terv kapcsán lehet ismerős az olvasóknak, ahol Teller Ede kutatócsoportjában dolgozott.) Steinhaus egy elegánsabb cukrászdát favorizált volna, de Banach ragaszkodott a kávéházhoz, ahol oldottabban lehetett matematikáról vitatkozni, inni, dohányozni, és sakkozni. Banach maga a többiektől függetlenül is rengeteg időt töltött a Rómában. Mivel az egyetemi fizetésből − különösen a hónap végén − nehezen lehetett kifizetni a fogyasztást, a hely tulajdonosa pedig meglehetősen rugalmatlan volt, Banach egy napon ráunt a kellemetlenségekre, és átsétált a néhány lépésre lévő Skót Kávéházba (Café Szkocka). Ez a nagyjából 50 fő befogadására alkalmas hely onnantól fogva a matematikus elit állandó gyülekezőhelyének számított. A társaság központi figurái: Banach, Mazur és Ulam, de mint később látni fogjuk, a legendás márványasztaloknál rengeteg világhírű matematikus megfordult, többek közt Neumann János és Maurice René Fréchet. A kávéházat vezető Tomasz Zielinski rugalmasságáról nem is a helyenként nagyvonalú számlakezelés árulkodik a legjobban, hanem az asztalok tisztántartása, vagy éppen tisztán nem tartása! Az asztalok ugyanis fehér márvánnyal voltak borítva, és a márványra jól lehetett írni puha ceruzával. Persze amilyen könnyű volt ráírni, olyan könnyű volt letakarítani, ezért néhány tragikus törlés után megkörnyékezték Zielinskit. Arra kérték, hogy a záróráig tartó összejövetelek után takarja le, vagy különítse el a teleírt asztalokat, nehogy a személyzet megsemmisítse a munkát. Így is történt, a következő nap délelőttjén pedig érkezett egy diák, és mindent lejegyzetelt.
2. A Skót Könyv
Vitán felül nagyon eredeti ez a munkafolyamat, de mint látjuk, elég sok szervezést igényel. Egyes elmondások szerint Zielinski panaszára Banach felesége, mások szerint maga Banach vásárolt egy kemény fedeles füzetet, amelybe azután a fontosabb problémákat feljegyezték. A füzet attól kezdve mindig a kávéházban volt elrejtve, a főpincértől lehetett kikérni, ha szükség volt rá. A napnál is világosabb, hogy egy ilyen szent tárgy neve nem lehet egyszerűen „a füzet”: az első oldalon Ksiega Szkocka, azaz Skót Könyv áll, csupa nagy betűvel. Az első tudományos bejegyzés 1935. július 17. dátummal szerepel:
Banach kérdése tömören így fogalmazható meg:
(a) Milyen feltételek mellett lehet egy (esetleg (B)-típusú) metrikus téren olyan új metrikát megadni, amellyel az már egyfelől teljes és kompakt, másfelől minden sorozat ami az eredeti metrika szerint konvergens volt, konvergens az új metrika szerint is? [A (B)-típusú tereket ma Banach tereknek nevezik.]
(b) A zérus sorozatok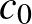 
terét lehet így metrizálni? [A 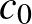tér eredeti távolsága ebben a kérdésben az egyenletes távolság.]
A probléma jóval bonyolultabb annál, mint hogy itt tárgyalhassuk, de a (b) pontról annyit legalábbis el lehet mondani, hogy 1957-ben oldotta meg egy Victor Klee nevű amerikai matematikus [4].
A Skót Könyvben összesen 193 probléma található, többnyire funkcionálanalízisből és topológiából. Néhányat ők maguk megoldottak a helyszínen, néhány a mai napig megoldatlan. A későbbiekben jónéhány problémát részletesen bemutatunk majd. Most csak egyet említünk meg érdekességként.
53. Probléma (RUZIEWICZ). Felbontható-e egy négyzet egymástól mind eltérő oldalhosszúságú négyzetek átfedés nélküli egyesítésére?
Ez egy roppant egyszerű fejtörő, bárki nekiugorhat! Aki ezt megteszi, némi próbálkozás után garantáltan elkezd majd gyanakodni, hogy ez a fejtörő az egyszerűtől meglehetősen távol van. Eleinte sokan azon a véleményen voltak (többek közt a legendás orosz matematikus Nikolai Luzin is), hogy ilyen felbontás nem létezhet. A sok megoldás közül egyet emelünk ki, 1948-ban Theophilus Harding Willcocks amatőr matematikus és sakkfanatikus megadta a négyzetnek egy olyan feldarabolását, ami 24 eltérő méretű négyzetből áll. Érdekesség, hogy Willcocks a megoldást egy tündérsakk magazinban hozta nyilvánosságra (Fairy Chess Review) [3].
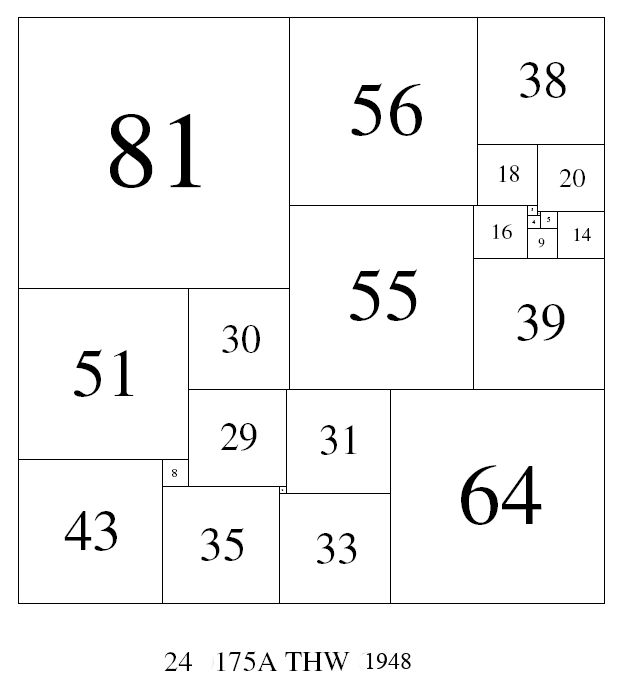
Akit ez a probléma jobban érdekel, nézze meg ezt a honlapot: http://www.squaring.net/sq/ss/s-pss.html.
A problémák mellé nemegyszer díjat is kitűztek. Általában egy-két üveg bort vagy sört (Neumann János whiskey-t), de volt néhány érdekesebb felajánlás is: Steinhaus 100 gramm kaviárt, Saks egy kiló bacont ajánlott jutalmul. (Ne felejtsük, hogy nagy világválság idején vagyunk!)
A legkülönösebb felajánlás kétség kívül Mazuré, aki 1936. november 6-án egy élő libát tűzött ki a 153. probléma megoldásáért. A megoldásra 1973-ig kellett várni: a legendás svéd matematikus Per Enflo ellenpéldát konstruált [1], ami rámutatott arra, hogy a 153-as problémában leírt approximációs tulajdonság nem mindig teljesül. A díjátadó ceremóniát akkor lengyelországszerte közvetítették, az alábbi kép pedig a mai napig gyakran felbukkan olyan előadásokban, amelyek bármilyen módon kapcsolatba hozhatók az approximációs problémával, vagy a Schauder-bázis létezésének problémájával.
A társaság történetére visszatérve: a náci megszállás elől többen emigráltak (Mazur például Neumann meghívására Princetonba ment), sokakat pedig ellehetlenítettek vagy meggyilkoltak. A legenda szerint magát a könyvet egy kapufa tövéhez közel ásták el egy bizonyos futballpályán. Akár így volt, akár nem, a könyv sikeresen túlélte a háborút, a szkennelt változata bárki számára elérhető.
A következő hónapokban az Érintő facebook oldalán rövid bejegyzések formájában folytatjuk a Skót Kávéház, illetve a Skót Könyv történetének bemutátását. Magáról a Skót Könyvről Daniel R. Mauldin szerkesztésében egy komoly kötet is megjelent, amelyben részleteen áttekintették rengeteg probléma történetét [2]. A kötetnek számos magyar vonatkozása van, ezekről is szó lesz: néhány problémát Buczolich Zoltán és Laczkovich Miklós tisztázott, egy egész fejezet szól Erdős Pál kedvenc könyvbéli problémáiról, és többször is feltűnik Neumann János neve.
Irodalomjegyzék
- [1] P. Enflo, A counterexample to the approximation problem in Banach spaces, Acta Mathematica, (1973) 130: 309–317.
[2] The Scottish Book Mathematics from The Scottish Café, with Selected Problems from The New Scottish Book, Springer International Publishing, Switzerland, 2015.
[3] T. H. Willcocks, Problem 7795 and solution, Fairy Chess Rev. 7 (1948), 97 (Aug.), 106 (Oct.).
[4] V. Klee, On a problem of Banach, Coll. Math. 5 (1957), 280–285.
A cikk az ITM és az NKFIH ÚNKP-20-5-BGE-1 és PD128374 kódszámú projektjeinek, valamint az MTA Bolyai János Kutatási Ösztöndíjának támogatásával készült.