Penrose munkássága előtt tisztelgő áttekintő írásunk első részében a fizikai Nobel-díjas matematikus főleg matematikai jellegű eredményeit (lehetetlen ábrák, kváziperiodikus csempézések és tvisztor-elmélet) tekintettük át [10]. A második részben elméleti fizikai, pontosabban gravitációelméleti erdeményeit vesszük közelebbről szemügyre; ezekért az 1960-70-es években folytatott vizsgálataiért nyerte el a fizikai Nobel-díjat 2020-ban.
1. Szingularitási tételek
A gravitáció modern elmélete Einstein általános relativitáselmélete, amelyet hosszú küzdelem után és a fizikus társadalom általános értetlenkedése közepette Einstein 1915-ben öntött végleges formába [11]. Az általános relativitáselmélet a klasszikus newtoni gravitáció-elmélet számos fogalmi nehézségét, valamint hibás kísérleti előrejelzését kiküszöböli; ennek viszont az az ára, hogy – a newtoni fizikával ellentétben – igen bonyolult matematikai apparátuson alapul: művelése a modern absztrakt differenciálgeometria és a nemlineáris parciális differenciálegyenletek elmélete szinte teljes fegyvertárának bevetését igényli. A mi szempontunkból most elegendő megemlíteni, hogy az általános relativitáselmélet alapfeltevése szerint a fizikai világ összes eseményei egy kauzális struktúrával ellátott négydimenziós kontinuumot alkotnak, a téridőt, amelynek matematikai modellje egy 
-dimenziós 
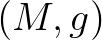Lorentz-sokaság: az 
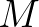differenciálható sokaság pontjai modellezik a fizikai eseményeket, a köztük levő ok-okozati viszonyokat pedig a 
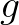Lorentz-metrika írja le, a gravitációs mezőt pedig a metrika 
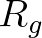Riemann-féle görbületi tenzora adja meg. A 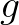kauzális szerkezet és ezzel az 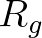gravitációs mező konkrét alakját az anyag téridőbeli eloszlása határozza meg (és fordítva) egy nagyon bonyolult másodrendű nemlineáris parciális differenciálegyenleten keresztül, ami az Einstein-egyenlet (a klasszikus gravitáció-elmélet Poisson-egyenletének messzemenő általánosítása.) Ennek az immár száz éves egyenletnek a vizsgálata a matematika máig aktívan kutatott, nyitott területe, véglegesnek tekinthető válaszok nélkül. Mindezek ellenére fogalmi egyszerűsége, szigorúan megalapozott matematikai háttere, valamint rendkívüli kísérleti jóslóereje az általános relativitáselméletet a fizika történetének talán esztétikailag legvonzóbb elméletévé teszi. Népszerűsítő bevezetés Einstein örökzöld könyvecskéje [1], egyetemi szintű fizikai-matematikai igényességű pedig pl. [12].
A természetben két makroszkopikus méretekben is jelen lévő kölcsönhatást ismerünk: az elektromágneses és a gravitációs kölcsönhatást. Míg az előbbi mind vonzó-, mind taszítóerő kifejtésére képes, a gravitációs erő mindig univerzális vonzóerőként jelentkezik. A gravitációs kölcsönhatás e tulajdonsága sajátos belső instabilitást eredményez, ami semmilyen más természeti erő esetében nem lép fel: nagy (csillagászati méretű) tömegek jelenlétében ez a nem kioltható vonzóerő olyan óriásivá fokozódhat, hogy minden más fizikai mechanizmust legyőzve a fizikai objektumot teljesen összeroppanthatja, valamiféle „kiterjedés nélküli” téridőbeli szingularitást hagyva csupán hátra. De miféle dolog egy ilyen „téridő-szingularitás” fizikai, ill. matematikai szempontból? Első ötletünk klasszikus elektrodinamikai ill. gravitációelméleti analógiák alapján a pontszerű töltések terében jelen lévő divergenciák mintájára az lenne, hogy a téridő azon tartományát kell szingulárisnak tekinteni, ahol a gravitációs térerősség, vagyis az Einstein-egyenlet 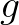megoldásából kapott 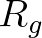görbületi tenzor divergál. Ilyen esetekben gyakran előfordul, hogy az 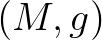téridő tartalmaz olyan megfigyelőt, egy 
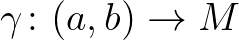differenciálható jövőirányú nemtérszerű görbét, ami úgy éri el a végtelen görbületű szinguláris tartományt, hogy közben a saját óráján csak véges idő telik el. Fizikailag szólva tehát található olyan fizikai objektum (akár egy űrhajós), amely a fizika törvényeinek megsértése nélkül saját ideje szerint véges (esetleg nagyon rövid) idő alatt elérheti a téridő végtelenül nagy gravitációs mezejű tartományait. Ez a lehetőség az ide érkező objektum feltehetően teljes fizikai megsemmisülésén túl azért is nyugtalanító, mert lehetőséget ad arra, hogy fizikai entitások véges idő alatt teljesen „eltűnjenek”, vagyis „kilépjenek a térből-időből”, „lemenjenek a térképről” stb. ami képtelenségnek tűnik. Tehát az Einstein-elmélet fizikai tartalma szempontjából döntő fontosságú a szingularitások meglétének-hiányának tisztázása az elméletben. Matematikailag (vagyis kevésbé drámaian) szólva az eddig elmondottak azt jelentik, hogy szingularitást tartalmazó 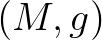Lorentz-sokaságokban létezhetnek nemmeghosszabítható de véges hosszúságú nemtérszerű 
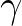görbék. Penrose nagy jelentőségű meglátása az volt, hogy így a gravitációs „téridő-szingularitás” fizikai szempontból nagyon nehezen körülhatárolható fogalma matematikailag megragadhatóvá válik, ha azt nem a görbület, hanem a görbék hossza felől fogjuk meg:
Definíció. Legyen 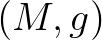egy olyan téridő, amely maximális, tehát tovább (pl. differenciálhatóan) nem terjeszthető. Ekkor 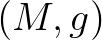szinguláris, ha mint Lorentz-sokaság nemtérszerűen nemteljes, pontosabban tartalmaz legalább egy olyan 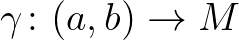differenciálható időszerű görbét vagy fényszerű geodetikust, mely (pl. differenciálhatóan) nemmeghosszabbítható, de 
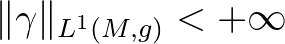. Itt
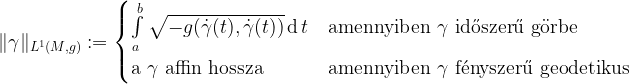
a 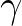görbe hosszát jelöli.
Fontos hangsúlyozni, hogy a definícióban végül is arról nem esik szó, hogy divergens-e az 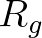görbületi tenzor vagy sem, vagyis hogy végül is milyen természetű a szingularitás: ennek vizsgálata további, esetleg nagyon bonyolult, meggondolásokat igényel. Kérdés mármost az, hogy a fizikai szempontból lényeges − pl. a csillagok gravitációs terét, vagy a Világegyetemet kozmikus léptékben leíró stb. − téridők szingulárisak-e a fentebbi egyszerű és általános értelemben. Az 1960-70-es években Penrose-t és akkori tanítványát, S. W. Hawkingot az Einstein-egyenlet megoldásainak beható tanulmányozása számos olyan „szingularitási tétel” megfogalmazására vezette, amelyek fizikailag fontos feltételek mellett garantálják szingularitások létezését. A szingularitási tételek, amik tehát differenciálgeometriai nyelven megfogalmazott és matematikai értelemben szigorúan bizonyított állítások, az alábbi sémára épülnek:
1. Tétel. Legyen 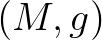egy olyan téridő, ami egy fizikailag releváns anyagmezőt vagy a vákuumot tartalmazó Einstein-egyenlet maximális, tehát tovább nem terjeszthető megoldása. Tegyük fel, hogy 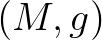ezen kívül eleget tesz bizonyos fizikai szempontból releváns és differenciálgeometriai nyelven jól megfogalmazható feltételeknek. Ekkor 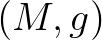szinguláris, vagyis tartalmaz legalább egy nemmeghosszabítható nemtérszerű 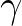görbét, amelynek hossza véges.
Sajnos e rövid áttekintésben e tételek pontos jelentését és sava-borsát (tehát erősségét) adó „fizikai szempontból releváns és differenciálgeometriai nyelven jól megfogalmazható” feltételek részletezésére nem térhetünk ki kifejezetten technikai jellegüknél fogva (de l. pl. [12, Chapter 9]). Mindenesetre e tételek fényében az Einstein-egyenlet „tipikus” megoldásai szingulárisak. Ez a tény fizikailag nem meglepő annak ismeretében amit a gravitáció univerzális vonzó jellegéről fentebb mondtunk; de matematikailag sem váratlan az eredmény hiszen Lorentz-sokaságokról van szó, és ezek körében nem igaz a Hopf-Rinow tétel (mely Riemann-sokaságok esetében tipikusan garantálja pl. a geodetikus teljességet).
Az első, immár tudománytörténeti jelentőségű szingularitási tételt Penrose bizonyította 1965-ben [7]. A Nobel Bizottság hivatalos indoklása szerint ezen eredményéből következő és 2019-ben kísérletileg is igazolt fizikai jóslatokért (fekete lyukak létezése, l. alább) nyerte el Penrose két másik tudóstársával a 2020-as Nobel-díjat. Azóta számos erősebb tétel-változat született, meg kell említeni ezek közül a Hawking-Penrose szingularitási tételt [5], amelyet a szerzők 1970-ben bizonyítottak be.
2. Kozmikus cenzor hipotézisek
A fentebbiekben a szingularitási tételek kapcsán az alábbi észrevételeket tettük: (i) a tételek azt mondják ki, hogy az Einstein-egyenlet fizikailag releváns megoldásai szingulárisak; (ii) egy szinguláris téridőben véges időn belül fizikai entitások „tűnhetnek el – jelenhetnek meg” a „semmiből” ami fizikai szerepüket igen kétségessé teszi (hiszen e téridők sértik az ok-okozatiság elvét); (iii) a szingularitási tételekben nincs szó a görbületi tenzor viselkedéséről; (iv) különböző „erősségű” szingularitási tételek léteznek.
Vizsgáljuk meg e kijelentéseket részletesebben. Az (i) észrevétel alapján az Einstein-elmélet matematikai szerkezete olyan, hogy az Einstein-egyenlet fizikailag releváns megoldásai kauzálisan nemteljesek, ez viszont (ii) alapján Einstein elméletét fizikai szempontból igen kétségessé teszi. Viszont nem szabad elfelejteni, hogy habár Penrose szingularitás-definíciója matematikai szempontból nagyon szabatos, fizikai szempontból esetleg túl általános, a (iii) szerinti értelemben. Valóban, az összes ismert igazán fontos, tehát nem csak valamiféle matematikai értelemben, hanem fizikai-csillagászati szempontból is jelentős de szinguláris Einstein-egyenlet megoldás kétféle osztályba sorolható: vagy ún. fekete lyuk vagy pedig. ún. kozmológiai típusú. Az előbbi típusba esnek a Schwarzschild, a Reissner-Nordstrøm valamint a Kerr és a Kerr-Newman téridők melyek különböző szimmetriájú, elektromosan semleges vagy töltött kompakt objektumok, pl. csillagok gravitációs tereit írják le. E megoldások közös tulajdonsága szinguláris jellegükön túl az, hogy bennük a görbületi tenzor is divergál, de úgy, hogy a tenzormező divergens része egy távoli megfigyelő számára nem észlelhető, mert azt egy, e tartományt körülvevő, ún. eseményhorizont mindig elrejti. Itt technikai okok miatt megintcsak nem definiáljuk, mit is értünk ezen (de l. pl. [12, Chapter 12]), hanem egy hasonlattal élünk: egy megfelelően görbült téridőben egy megfigyelő szempontjából létezhetnek nem megfigyelhető események pontosan úgy, mint ahogy egy valahol az Alföldön álló szemlélő számára bizonyos túl messzi, „horizonton túli” tereptárgyak már nem láthatóak a földfelszín görbültsége miatt. Egy ilyen téridőben az eseményhorizonton túli történések, események összességét fekete lyuknak nevezzük és azt mondjuk, hogy ez a téridő fekete lyukat tartalmaz. Tehát amennyiben egy téridő úgy szinguláris, hogy benne a kauzálisan problematikus tartományok mind fekete lyukak mélyén helyezkednek el, vagyis egy szokványos megfigyelő elől eseményhorizontok által mindig rejtve maradnak, akkor ezt a helyzetet kauzalitási szempontból végül is nem tartjuk aggályosnak. Fontos hangsúlyozni, hogy a fentebbi téridők szinguláris jellege és bennük eseményhorizontok létezése látszólag egymástól teljesen függetlenek, mindkét megnyilvánulás az Einstein-egyenlet két szubtilis és látszólag független tulajdonsága, ezek együttes megjelenésére viszont egy fizikailag releváns megoldásban az ok-okozatisági elv effektív teljesülése szempontjából szükség van.
Az utóbbi, tehát a kozmológiai típusú szingularitásokra példa a modern kozmológia standard modelljének számító Friedman-Lemaître-Robertson-Walker téridő, ami az általunk megfigyelhető Világegyetem nagybani, homogén és izotrópnak látszó szerkezetét modellezi. Ez a téridő szintén szinguláris és benne a görbület divergál, de úgy, hogy a kauzalitás-sértés minden lehetséges megfigyelő számára annak múltjában található (tehát elvben „látható”). Egy kozmológiai szingularitást tartalmazó téridőben tehát kauzalitás-sértési szempontból „mindössze” annyi történhet, hogy „minden egyszerre csak megjelenik” (Ősrobbanás). Ismét meg kell jegyezni, hogy a kauzalitás-sértés pontosan efféle jellege látszólag véletlen, az Einstein-egyenlet szerkezete ezt a priori nem garantálja. Emiatt is Penrose-t sokat foglalkoztatta az, hogy a szingularitási tételek által feltárt és generikusnak tekinthető kauzalitás-sértési lehetőségek az általános relativitáselméletben minden esetben a fentebbi két biztonságos osztályba esnek-e, ami tehát azt jelenti, hogy tipikus megfigyelő elől „eltakartak” ill. általa „nem vehetők igénybe”. Jobb híján tehát elvként ki kell kötnünk, nagyon vázlatosan fogalmazva, hogy fennáll:
Kozmikus cenzor hipotézisek. A fizikai világ térideje olyan, hogy az egyetlen kozmológiai típusú, tehát elvben látható múltbeli (Ősrobbanás) szingularitáson kívül csakis fekete lyuk típusú, tehát nem látható (mert eseményhorizontok mögé rejtett) szingularitásokat tartalmaz.
A hipotézist szokás erős és gyenge változatban kimondani, ill. egyre finomabb precíz matematikai alakok is léteznek, ezekre azonban itt nem térhetünk ki (de l. pl. [12, Section 12.1]). Az erős változat megfogalmazása Penrose egyik 1979-es dolgozatában található meg először [8]. Az elmúlt fél évszázad során mind a fizikusok, mind a matematikusok nagy erőkkel dolgoztak a kozmikus cenzor hipotézisek valamely változatának bizonyításán – vagy éppen ellenkezőleg: cáfolatán. Azt lehetne mondani, hogy míg a hipotézisek megfogalmazása idején, tehát a korai 1970-80-as években mindenki meg volt győződve a hipotézisek (valamely formájának) igazságáról, manapság a helyzet egyre kevésbé világos [2,3,4,9].
Érdemes röviden kitérni a hipotézisek elnevezésének eredetére. Egy elvben máig érvényben lévő XVI. századi rendelet szerint az angol királyság területén működő színházakban tilos a nyíltszíni meztelenkedés. De mivel ezt gyakran megsértették, azt is elrendelték, hogy minden egyes előadás alkalmával a nézőtér első sorában egy ülőhelyet fent kell tartani a hivatalos királyi cenzor számára, akinek feladata, hogy egy pokróccal kezében az előadást figyelje és ha meztelenkedésre kerülne sor, akkor azonnal a színpadra lépjen és mindenkit letakarjon – lehetőleg az előadás megzavarása nélkül.
A most leírtak motivációul szolgálnak a szingularitási tételek, ill. a kozmikus cenzor hipotézisek bizonyos kurrens továbbfejlődési irányainak áttekintéséhez, amikre a (iv) pontban utaltunk. Egy szingularitási tétel „erejét” az dönti el, hogy a benne szereplő „fizikai szempontból releváns és differenciálgeometriai nyelven jól megfogalmazható” feltételek mennyire lokális (tehát nem globális) jellegűek, ui. egy konkrét megfigyelőnek (pl. űrhajósnak) csupán a téridő lokális tulajdonságainak meghatározására van lehetősége, efféle mérésekből kell kitalálnia, hogy pl. a körülötte elhelyezkedő ismeretlen téridő-tartomány tartalmaz-e fekete lyukat vagy sem. Nem túlzás azt állítani, hogy a kérdés helyes megválaszolása egy eljövendő űrhajós számára kulcsfontosságú lehet. Az eredeti Penrose-, ill. Hawking-Penrose-féle és viszonylag könnyen bizonyítható szingularitási tételek még sok olyan feltevést tartalmaznak, amelyek globálisak (pl. hogy a teljes téridő globálisan hiperbolikus, benne a Cauchy-felületek nem kompaktak, stb.). Az ilyen feltevések egy lokális megfigyelő szempontjából praktikusan nem eldönthetőek, a priori adottnak tekintendők. Pl., ha a priori tudjuk, hogy a téridő tartalmaz egy fekete lyukat, akkor egy ilyen fekete lyuk látványa megfesthető. Kip Thorne amerikai fizikus (aki 2017-ben kapott fizikai Nobel-díjat a 2016-ban kísérletileg szintén kimutatott, összeütköző fekete lyukak keltette gravitációs hullámok megjóslásáért) számításai és instrukciói alapján az Interstellar (Csillagok között) c. 2014-es erősen hollywoodi jellegű filmben megjelenik egy tudományos szempontból korrekt feketelyuk-ábrázolás (l. 1. ábra).
Mit látunk ezen a festményen? Egy forgó fekete lyuk képét látjuk, amelynek forgástengelye egy, a kép síkjába eső függőleges egyenes, és a rá merőleges egyenlítői síkban a fekete lyukat egy izzó gázokból álló ún. akkréciós korong veszi körül. Hawking egy alapvető fontosságú tétele szerint a fekete lyuk eseményhorizontja egy téridőbe ágyazott (vagy esetleg csak immertált) felület, amely mindig homeomorf egy kédimenziós gömbbel. Az 1. ábrán ezt a gömböt fekete korong szemlélteti, „azon túl” van a fekete lyuk. Egy szokásos gömb szemlélésével ellentétben viszont e látvány rendkívüli tulajdonságokkal bír: nemcsak az eseményhorizont felénk néző „eleje”, hanem a „hátulsó fele” is látszódik, hiszen a fekete lyuk hatalmas gravitácós tere a hátrafelé induló fotonok egy részét is „visszafordítja” felénk (emiatt látunk egy fényes korongot a merőleges síkban is, ami nem más, mint az eredeti akkréciós korong „hátsó fele”).
Abban a szerencsés helyzetben vagyunk, hogy ezt a képet már össze tudjuk hasonlítani egy tőlünk kb. 53 millió fényévnyire lévő igazi és nagyon aktív szuperóriás fekete lyuk portréjával (l. 2. ábra). A híres felvétel 2019 májusában járta be a világsajtót és Penrose Nobel-díjának kísérleti alapját is adja.
Mielőtt tovább mennénk, meg kell említeni, hogy a 2020-as fizikai Nobel-díj két másik kitüntetettje: Andrea Ghez amerikai és Reinhard Genzel német fizikusok e kép megszületésében játszott szerepükért nyerték el a rangos elismerést. Visszatérve, ez a kép már nem annyira meggyőző, mint az előző; pl. összevetve a tőlünk kb. 640 fényévre található haldokló vörösóriás csillag, a Betelgeuse (az Orion-alak jobb válla) szintén 2019-ben készült fényképével (l. 3. ábra) némi hasonlóságot is vélünk felfedezni (minden bizonnyal még jobban hasonlító csillagászati felvételeket is találhattunk volna).
Felvetődik hát a kérdés: léteznek-e praktikus szingularitási tételek, amik tehát tisztán lokális tulajdonságokból eldöntik, hogy egy adott téridő-tartomány tartalmaz-e fekete lyukat vagy csak egy arra nagyon hasonlító valamit? Véleményünk szerint komoly óvatosságra int, hogy ilyen tételek nem léteznek: friss eredmények [6] szerint egy a priori ismereteket nem feltételező, tehát tisztán csak lokális tulajdonságokat meghatározni képes megfigyelő egy téridő tartományról csak akkor tudja biztosan eldönteni, hogy tartalmaz-e fekete lyukat, ha a fekete lyuk belsejében is meghatároz bizonyos lokális tulajdonságokat [6, Section 6]. Másként fogalmazva: egy űrhajós csak akkor bizonyosodhat meg egy közeli fekete lyuk ottlétéről, ha már nem tudja azt többé elhagyni!
Irodalomjegyzék
- [1] Einstein, A.: A speciális és általános relativitás elmélete, Gondolat, Budapest (1963).
[2] Etesi, G.: A proof of the Geroch-Horowitz-Penrose formulation of the strong cosmic censor conjecture motivated by computability theory, Int. Journ. Theor. Phys. 52, 946-960 (2013).
[3] Etesi, G.: Exotica and the status of the strong cosmic censor conjecture in four dimensions, Class. Quant. Grav. 34, 245010 (2017).
[4] Etesi, G.: Global solvability of the vacuum Einstein equation and the strong cosmic censorship in four dimensions, Journ. Geom. Phys. 164, 104164 (2021).
[5] Hawking, S.W., Penrose, R.: The singularities of gravitational collapse and cosmology, Proc. Roy. Soc. London A314, 529–548 (1970).
[6] Müller, O.: Black holes in Einstein-Maxwell theory, Class. Quant. Grav. 36, 015002 (2019).
[7] Penrose, R.: Gravitational collapse and space-time singularities, Phys. Rev. Lett. 14, 57–59 (1965).
[8] Penrose, R.: Singularities and time asymmetry, in: General relativity, an Einstein centenary survey (ed. S. W. Hawking, W. Israel), Cambridge Univ. Press, Cambridge (1979).
[9] Penrose, R.: The question of cosmic censorship, Journ. Astrophys. Astr. 20, 233-248 (1999).
[10] Szabó Sz.: Roger Penrose, az első Nobel-díjas matematikus, 1. rész, megjelent az Érintő 2020 decemberi számában.
[11] Vizgin, V.P.: A modern gravitációelmélet kialakulása, Gondolat, Budapest (1989).
[12] Wald, R. M.: General relativity, Chicago Univ. Press, Chicago (1984).