Bevezetés
Közismert tény, hogy matematikából nem osztanak Nobel-díjat, így csekély az esélye, hogy egy matematikust kitüntessenek vele. Bizonyos értelemben idén először mégis ez történt: Roger Penrose elnyerte a fizikai Nobel-díjat.
A fenti kijelentés kétfelől is megkérdőjelezhető, ezért helyes értelmezése némi magyarázatra szorul. Egyrészről megkérdőjelezhető, hogy idén először történt-e ilyen: felvethető például a lineáris programozási feladat mellett többek között az optimális szállítási feladatról [3] is ismert Leonyid Vitalijevics Kantorovics, valamint az Egy csodálatos elme című film főhőse, a metrikus differenciálgeometriában is jelentős eredményeket elért John Nash esete, akik 1975-ben illetve 1994-ben matematikus létükre megkapták a közgazdaságtani Nobel-díjat, és akik azóta is matematikusok generációinak munkáját inspirálták. Ez ugyan igaz, azonban (minden elismerésünk mellett) a közgazdaságtani Nobel-díj szigorú értelemben véve nem egyike az Alfred Nobel által végrendeletében eredetileg meghagyott díjaknak, hanem a Svéd Jegybank által, megalapításának 300-adik évfordulója alkalmából, A. Nobel tiszteletére létrehozott díj [1].
A másik lehetséges ellenvetés a fenti állítással szemben az, hogy mennyiben tekinthető Penrose matematikusnak. Kétségtelen, hogy a díjat a bizottság a fizikai munkásságára ítélte, egész pontosan „annak felfedezéséért, hogy a fekete lyuk kialakulása az általános relativitáselmélet robusztus előrejelzése” [2]. Mindazonáltal, az angolszász tudományos közéletben nincs éles határvonal a matematika és fizika között. Gondoljunk csak Sir Isaac Newton-ra, aki egyaránt alkotott rendkívül jelentőset mindkét tudományban. (Hasonló igaz egyébiránt más országokban is, pl. a francia Joseph-Louis Lagrange, vagy éppen Neumann János esetében, és a sort hosszan folytathatnánk.) Jóllehet, manapság talán ritkább az ilyen multidiszciplináris tudós, ám Sir Roger Penrose éppen a kivételek egyike, és talán túlzás nélkül az egyik legnagyobbika. Mi sem bizonyítja ezt jobban, mint az, hogy matematikus egyetemi végzettsége és algebrai geometriából szerzett PhD fokozata után egyaránt közölt matematikai és fizikai témájú eredményeket. Munkahelye az Oxfordi Egyetem Matematika Intézete volt, ahol jelenleg emeritus professzor, eddigi elismerései között pedig éppúgy találunk matematikaiakat (Clay Award for Dissemination of Mathematical Knowledge (2018), De Morgan medal (2004) és Naylor Prize (1991), London Mathematical Society), mint fizikaiakat (Dirac Medal for the Advancement of Theoretical Physics (2006) és Einstein Medal, Albert Einstein Society (1990)).
Életműve rendkívül szerteágazó, az algebrai geometriától a diszkrét geometrián és differencálgeometrián keresztül a kozmológiáig, sőt egészen az emberi tudat fizikájáig számos témát felölel. Ezen cikkben a matematikailag jelentős eredményei közül mutatunk be néhányat.
Lehetetlen ábrák
Penrose egyetemi tanulmányai alatt 1954-ben Amszterdamban járt, ahol megtekintette az akkoriban már elismert Maurits Cornelis Escher holland grafikus egy kiállítását, amelyen valószínűleg látott kiállítva a művész akkoriban már létező lehetetlen ábrái (pl. Relativiteit (1953)) közül néhányat. Egy ábrát akkor nevezünk lehetetlennek, ha minden kellően kicsiny részlete valamely térbeli test vetülete, ám nem létezik olyan térbeli test, amelynek egészében véve vetülete lenne. (Mellékesen megjegyezzük, hogy lehetetlen ábrát Escher előtt már a svéd Oscar Reutervärd is alkotott.) Ez az élmény annyira lenyűgözte, hogy édesapjával, a matematikus, genetikus, pszichiáter Lionel Penrose-zal közösen szerkesztett egy folytonosan emelkedő, önmagába visszatérő lépcső ábráját, amely matematikailag a Penrose-háromszög nevű alakzattal egyenértékű.

A Penrose-háromszög (Forrás: https://en.wikipedia.org/wiki/Roger_Penrose#/media/File:Penrose-dreieck.svg)
Az ebből írt cikket [5] elküldte Eschernek, aki ennek hatására további lehetetlen ábrákat tartalmazó metszeteket (Klimmen en daalen – Ascending and Descending (1960), Waterval – Waterfall (1961)) készített.

M. C. Escher: Waterval – Waterfall – Vízesés (Forrás: https://en.wikipedia.org/wiki/Waterfall_(M._C._Escher)#/media/File:Escher_Waterfall.jpg)
Egy későbbi írásában [7] Roger Penrose visszatér a lehetetlen ábrák témájához, ezúttal azonban azok algebrai topológiai elméletét dolgozza ki. A lokális adatok egy nagy egésszé való összeilleszthetőségére vonatkozó feltételek ugyanis az algebrai topológia eszközeivel, azon belül is leggyakrabban a homológia- illetve kohomológia-elméletekkel fogalmazhatók meg. Röviden összefoglaljuk ezt az elméletet. Legyen 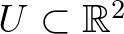 egy összefüggő, de nem egyszeresen összefüggő nyílt halmaz (a Penrose-háromszög esetében
egy összefüggő, de nem egyszeresen összefüggő nyílt halmaz (a Penrose-háromszög esetében 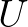 egy körgyűrű). Legyen továbbá
egy körgyűrű). Legyen továbbá 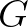 egy Abel-csoport (a Penrose-háromszög esetében
egy Abel-csoport (a Penrose-háromszög esetében 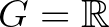 ). Fedjük le
). Fedjük le  -t véges sok
-t véges sok  nyílt halmazzal úgy, hogy bármely két részhalmaz metszete pontra húzható legyen (például, esetünkben
nyílt halmazzal úgy, hogy bármely két részhalmaz metszete pontra húzható legyen (például, esetünkben  mellett lásd a következő ábrát).
mellett lásd a következő ábrát).
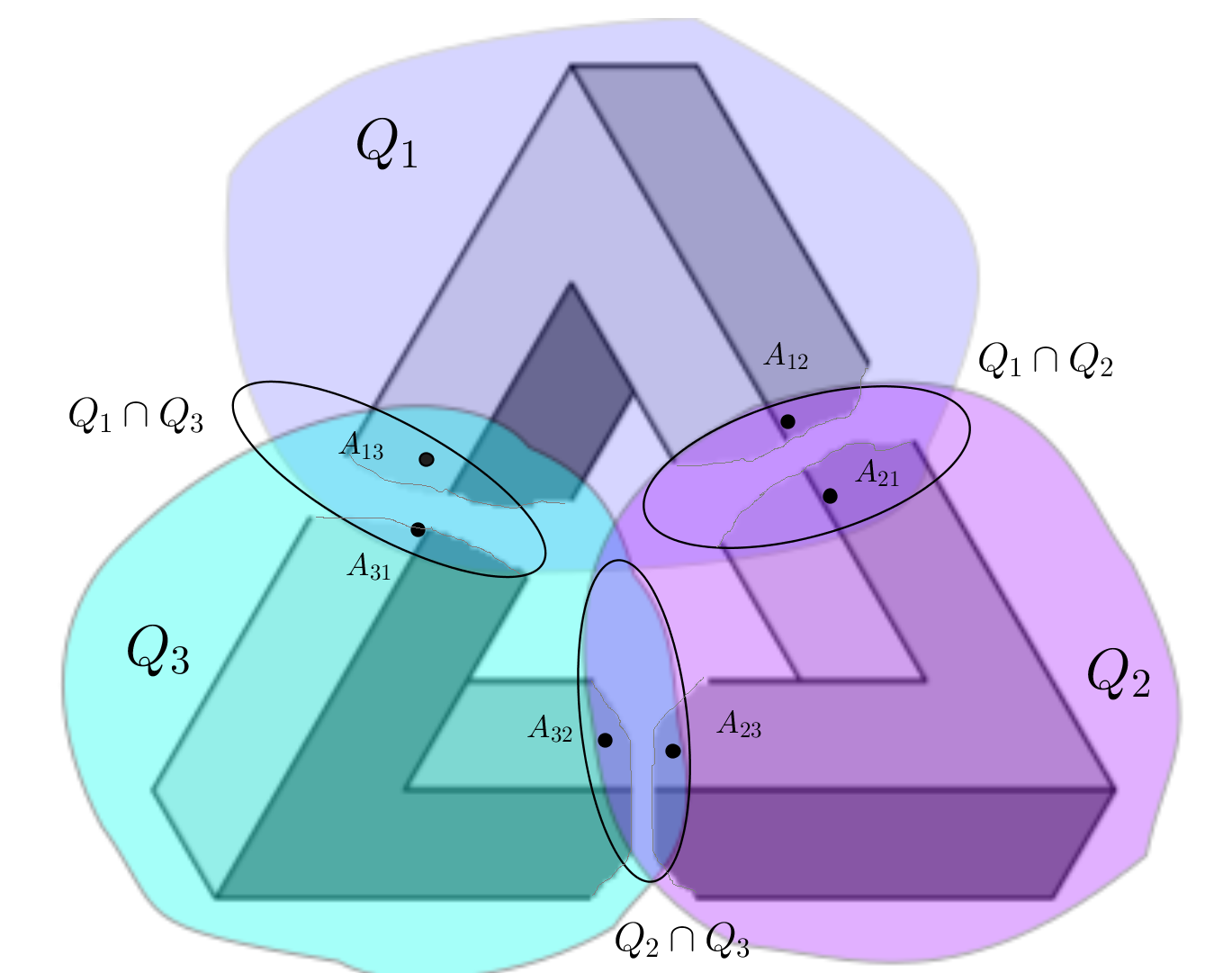
A körgyűrű fedése három pontra húzható nyílt halmazzal. Készítette: Marco Biemann.
Az egyszerűség kedvéért feltesszük, hogy 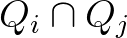 akkor és csak akkor nem üres, ha
akkor és csak akkor nem üres, ha 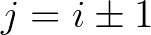 (ahol
(ahol 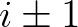 -et modulo
-et modulo  értjük), továbbá hogy
értjük), továbbá hogy 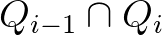 minden
minden  -re pontra húzható. Legyen minden
-re pontra húzható. Legyen minden  -n adott egy
-n adott egy  térbeli merev test síkbeli vetületének ábrája, amelyekre teljesül, hogy minden
térbeli merev test síkbeli vetületének ábrája, amelyekre teljesül, hogy minden  -re a
-re a 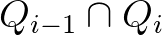 metszeten a
metszeten a 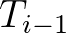 és
és 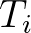 vetületei egybevágók. Irányítsuk valahogyan a síkra merőleges
vetületei egybevágók. Irányítsuk valahogyan a síkra merőleges 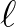 egyenest, és jelöljük
egyenest, és jelöljük  -vel a
-vel a 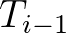 és
és 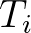 közötti előjeles távolságot
közötti előjeles távolságot 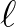 adott irányítására nézve. Mármost, ha a különböző
adott irányítására nézve. Mármost, ha a különböző 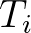 -k egyazon
-k egyazon  -beli
-beli  merev tárgynak a rögzített síkra vett vetületének részei, akkor nyilvánvalóan minden
merev tárgynak a rögzített síkra vett vetületének részei, akkor nyilvánvalóan minden  -re
-re 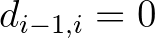 . Elképzelhető persze, hogy ahhoz, hogy a
. Elképzelhető persze, hogy ahhoz, hogy a 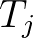 tárgyak összeálljanak egyetlen
tárgyak összeálljanak egyetlen  tárggyá, néhány
tárggyá, néhány 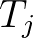 tárgyat
tárgyat 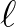 mentén valamekkora
mentén valamekkora  távolsággal el kell tolni. Ezen eltolás eredményeképpen nyilván a
távolsággal el kell tolni. Ezen eltolás eredményeképpen nyilván a 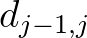 viszonylagos távolság
viszonylagos távolság  -vel növekszik, míg a
-vel növekszik, míg a 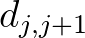 mennyiség
mennyiség  -vel csökken, végül, a többi
-vel csökken, végül, a többi 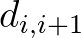 távolság pedig változatlan marad. Gondolatmenetünkből látszik, hogy akkor és csak akkor létezik olyan
távolság pedig változatlan marad. Gondolatmenetünkből látszik, hogy akkor és csak akkor létezik olyan  tárgy, amelynek vetülete minden
tárgy, amelynek vetülete minden 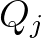 -n
-n 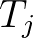 , ha léteznek olyan
, ha léteznek olyan 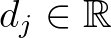 értékek (
értékek ( 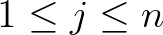 ), hogy minden
), hogy minden 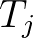 -t
-t  -vel eltolva minden
-vel eltolva minden  -re teljesül
-re teljesül 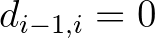 . A
. A 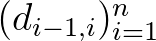 szám
szám 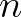 -es, a
-es, a  távolságokkal való eltolások erejéig, éppen
távolságokkal való eltolások erejéig, éppen 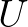 -nak az
-nak az 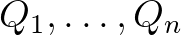 fedésére vonatkozó ún.
fedésére vonatkozó ún. 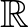 -együtthatós első Čech kohomológia-csoportjának egy elemét adja. Ismert az algebrai topológiából, hogy egy nem egyszeresen összefüggő síkbeli tartományra ez a csoport nem-triviális (a körgyűrűre például pontosan
-együtthatós első Čech kohomológia-csoportjának egy elemét adja. Ismert az algebrai topológiából, hogy egy nem egyszeresen összefüggő síkbeli tartományra ez a csoport nem-triviális (a körgyűrűre például pontosan 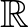 ). Valóban, a
). Valóban, a 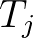 tárgy
tárgy  -vel való eltolásának hatása a
-vel való eltolásának hatása a 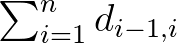 mennyiséget nem változtatja meg; könnyen végiggondolható másrészt, hogy ezen összeg az egyetlen akadálya annak, hogy két
mennyiséget nem változtatja meg; könnyen végiggondolható másrészt, hogy ezen összeg az egyetlen akadálya annak, hogy két 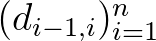 szám
szám 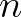 -est alkalmas
-est alkalmas  távolságokkal való eltolásokkal egymásba vigyünk. Azt kapjuk végeredményben, hogy egy lokálisan koherens ábrának akkor és csak akkor létezik ellentmondásmentes térbeli realizációja , ha az egyes részek egymáshoz való viszonylagos távolságainak összege 0. Escher lehetetlen ábráiban ez a mennyiség (amely értelmezhető pl. a Vízesésben a víz szintjének globális emelkedéseként) nem 0, ezért nem létezhetnek olyan 3-dimenziós alakzatok, amit ábrázolnának.
távolságokkal való eltolásokkal egymásba vigyünk. Azt kapjuk végeredményben, hogy egy lokálisan koherens ábrának akkor és csak akkor létezik ellentmondásmentes térbeli realizációja , ha az egyes részek egymáshoz való viszonylagos távolságainak összege 0. Escher lehetetlen ábráiban ez a mennyiség (amely értelmezhető pl. a Vízesésben a víz szintjének globális emelkedéseként) nem 0, ezért nem létezhetnek olyan 3-dimenziós alakzatok, amit ábrázolnának.
Azon ábrákra, amelyek lehetetlensége abban nyilvánul meg, hogy egy bizonyos alakzat alját vagy tetejét látjuk-e, hasonló érvelés érvényes a 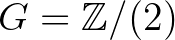 kételemű csoporttal.
kételemű csoporttal.
Aperiodikus csempézések
A sík sokszögekkel való hézagmentes, át nem fedő kitöltését csempézésnek, egy csempézésben szereplő sokszögeket pedig az adott csempézés csempéinek nevezünk. Egy csempézést végesnek mondunk, ha csempéinek halmaza egybevágóság erejéig véges. Egy csempézést periodikusnak hívunk, amennyiben létezik két, egymással nem párhuzamos irányú eltolás, amely a csempézést önmagába viszi át (a csempék halmazát permutálja); ellenkező esetben a csempézést aperiodikusnak hívjuk.
A csempézések Kepler óta foglalkoztatják a matematikusok és művészek fantáziáját, utalhatunk például ismét Escher metszeteire.

Escher szabályos háromszögcsempézést illusztráló műve (Forrás: https://www.pleacher.com/mp/escher/reptile2.jpg (David Pleacher: Art of M C Escher)
Már Kepler is tudta, hogy amennyiben egy periodikus csempézés minden csempéje egybevágó szabályos sokszög, akkor ezek szükségszerűen szabályos háromszögek, négyzetek vagy szabályos hatszögek. (Az, hogy ilyen szabályos sokszögekkel valóban létezik periodikus csempézés, a négyzetminta esetén nyilvánvaló, a hatszög esetére ismert néhány fürdőszoba-padlóról és a méhkasok mintájáról, a háromszög esetén pedig például a szabályos hatszöggel való csempézésből és a szabályos hatszög hat szabályos háromszögre való oszthatóságából azonnal adódik.)
Érdekes következménye a fent említett ténynek, hogy szabályos ötszögekkel a sík nem csempézhető. Érvényes ugyanis a kristálytani korlátozásra vonatkozó tétel [4, 4.5. Fejezet]: Bármely kétdimenziós rács (azaz két, egymással nem párhuzamos eltolásra invariáns diszkrét ponthalmaz) bármely forgásszimmetriájának rendje 2, 3, 4 vagy 6. Azonban, Kepler 1619-ben azt is megmutatta, hogy szabályos ötszögekkel és további alakzatokkal (többek között pentagramokkal és szabályos tízszögekkel) a sík csempézhető. Érdekességként megjegyezzük, hogy a középkori iszlám díszítőművészetben is található ilyen csempézés, az ehhez használt csempéket girih-nek nevezik.
Kepler ezen gondolatai inspirálták R. Penrose-t, amikor 1974-ben elkészítette a sík egy olyan (aperiodikus) csempézését, amelyben három más alakzat mellett szabályos ötszögek is szerepelnek [8]. Ebben a csempézésben tehát egybevágóság erejéig összesen négy sokszög szerepel. Ezt a konstrukcióját továbbfejlesztve később további aperiodikus csempézéseket konstruált, lecsökkentve az ezekben szereplő sokszögek számát kettőre.
A lenti ábrán bemutatott P2 jelű csempézésben például két deltoid szerepel: egy konvex ún. sárkány (kite) és egy konkáv ún. nyílhegy (dart).

Egy P2 csempézés részletei (Forrás: https://upload.wikimedia.org/wikipedia/commons/3/3e/RectangleFill.gif. Készítette: Przemek Majewski)
Mindkét deltoid a szimmetriatengelye mentén két egybevágó aranyháromszögre (azaz, olyan egyenlőszárú háromszögre, amelyek alapja és szára egymáshoz az aranymetszés 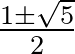 aránypárjában viszonyulnak) bomlik fel: a sárkány hegyesszögűekre, míg a nyílhegy tompaszögűekre, lásd a következő ábrát.
aránypárjában viszonyulnak) bomlik fel: a sárkány hegyesszögűekre, míg a nyílhegy tompaszögűekre, lásd a következő ábrát.
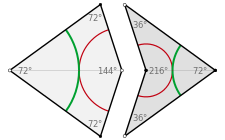
A sárkány és nyílhegy négyszögek (Forrás: https://commons.wikimedia.org/wiki/File:Kite_Dart.svg. Készítette: Geometry Guy)
Az ezeket alkotó aranyháromszögek szögei a sárkány esetében 36, 72, 72 fokosak, míg a nyílhegyre ezek az értékek rendre 108, 36, 36. A felhasznált sárkány és nyílhegy rövidebb és hosszabb oldalhosszai megegyeznek. Azonnal látszik, hogy ekkor egy sárkányból és egy nyílhegyből összeállítható egy 72 és 108 fokos szögű rombusz, amelyből persze periodikus csempézés készíthető (mint bármely parallelogrammából). Annak érdekében tehát, hogy a kapott csempézés aperiodikus legyen, meg kell tiltani a csempék bizonyos összeillesztéseit. Az engedélyezett illesztéseket szokás például a négyszögekbe rajzolt, egyes éleket összekötő színes körívekkel jelölni: akkor és csak akkor szabad két négyszöget egymáshoz illeszteni egy él mentén, ha a két csempén az adott élt metsző azonos színű körívek egymással összeillenek; ilyen körívek vannak a fenti ábrán. Ez a megkötés csupán a következő ábrán bemutatott hét lehetőséget engedi meg a csúcsok körüli csempe-konfigurációknak.
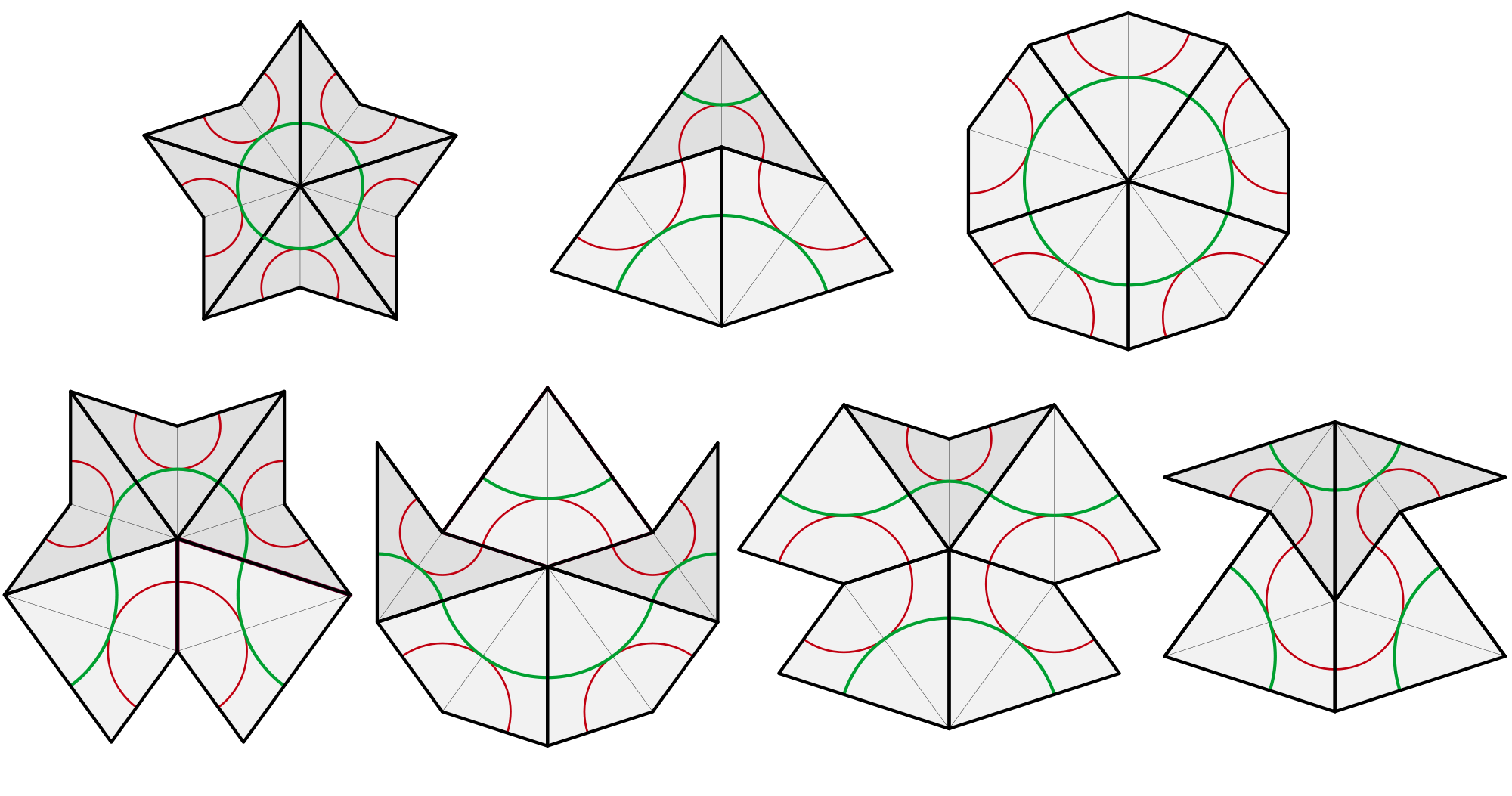
A csúcsok körüli lehetséges illesztések (Forrás: Penrose vertex figures Wikimedia Commons)
Bebizonyítható, hogy ezzel a megkötéssel is létezik csempézés sárkányokkal és nyílhegyekkel, sőt, megszámlálhatatlanul végtelen sok egymással nem egybevágó ilyen csempézés létezik. Első ránézésre ezeknek a P2 csempézéseknek nincs sok közük a szabályos ötszögeket felhasználó csempézésekhez. Penrose és az előző lapszámban [10] méltatott John Conway azonban bebizonyították, hogy amennyiben a lapokra rajzolt színes körívekből álló valamely görbe zárt, akkor annak belseje az ötödrendű diéder-csoportra (azaz, a szabályos ötszög 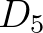 szimmetriacsoportjára) nézve invariáns; ráadásul, bármely P2 csempézésben mindkét színű görbéből legfeljebb kettő létezhet, amelyek nem záródnak. A legszimmetrikusabb esetben a teljes csempézés invariáns a
szimmetriacsoportjára) nézve invariáns; ráadásul, bármely P2 csempézésben mindkét színű görbéből legfeljebb kettő létezhet, amelyek nem záródnak. A legszimmetrikusabb esetben a teljes csempézés invariáns a 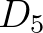 csoportra, ilyen csempézés pontosan kettő létezik.
csoportra, ilyen csempézés pontosan kettő létezik.
Az aperiodikus csempézések nem csupán elszigetelt matematikai kuriózumok: a teljesség igénye nélkül, olyan távolinak tűnő matematikai területekhez kapcsolódnak szervesen, mint a matematikai logikai döntési feladatok és a nemkommutatív geometria, a fizikában pedig az először 1982-ben megfigyelt kvázikristályok matematikai modelljei.
Tvisztorok
Egy 1967-es dolgozatában [6] Penrose bevezette a tvisztor-tér fogalmát, amely remekül illusztrálja, hogy munkássága egyszerre fizikai és matematikai jellegű. Amint azt később írta [9], e fogalom bevezetésével célja olyan alapvető fizikai problémák feloldása volt, mint például a kvantum-mezőelmélet végtelen mennyiségeinek megszüntetése, visszavezetni valamely alapelvre a csatolási állandók és elemi részecskék tömegének értékét, találni egy olyan kvantum-gravitáció elméletet, amely kompatibilis a téridő szingularitásaival stb. Ahogy azonban ugyanitt megjegyzi, ezen elmélet alkalmazásai ezidáig szinte kizárólag a matematikán belül találhatók.
Az eredeti konstrukció a lapos Minkowsi-téridőre vonatkozott, ám – mint az később kiderült – természetesen általánosítható bármely félig konformálisan lapos 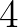 -dimenziós teljes
-dimenziós teljes 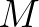 Riemann-sokaságra. A félig konformálisan lapos jelző azt jelenti, hogy a görbülettel kompatibilis, ún. Levi–Civita konnexió irreducibilis felbontásában az egyik tenzor (a
Riemann-sokaságra. A félig konformálisan lapos jelző azt jelenti, hogy a görbülettel kompatibilis, ún. Levi–Civita konnexió irreducibilis felbontásában az egyik tenzor (a 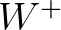 pozitív Weyl-tenzor) eltűnik. (Ezekről a fogalmakról és eredményekről bővebben lásd korábbi cikkünket [11].) Tekintsük ekkor
pozitív Weyl-tenzor) eltűnik. (Ezekről a fogalmakról és eredményekről bővebben lásd korábbi cikkünket [11].) Tekintsük ekkor 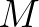 érintőnyalábjának komplexifikáltját. Ha
érintőnyalábjának komplexifikáltját. Ha 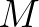 spin sokaság, akkor ez a nyaláb felbomlik két
spin sokaság, akkor ez a nyaláb felbomlik két  -rangú komplex vektornyaláb összegére, amelyeket ekkor pozitív illetve negatív spinor-nyalábnak nevezünk, és
-rangú komplex vektornyaláb összegére, amelyeket ekkor pozitív illetve negatív spinor-nyalábnak nevezünk, és 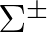 -val jelölünk. A Levi–Civita konnexió indukál egy-egy konnexiót
-val jelölünk. A Levi–Civita konnexió indukál egy-egy konnexiót 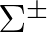 -on. Ekkor
-on. Ekkor 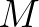 tvisztor-tere a
tvisztor-tere a 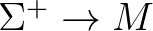 nyaláb fibrumonkénti
nyaláb fibrumonkénti 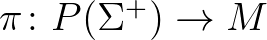 projektivizáltjának
projektivizáltjának  -vel jelölt teljes tere (amely nem-spin
-vel jelölt teljes tere (amely nem-spin 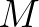 esetén is értelmezett). A tvisztor-tér tehát egy fibrálás
esetén is értelmezett). A tvisztor-tér tehát egy fibrálás  felett, amelynek fibrumai
felett, amelynek fibrumai 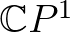 komplex projektív egyenesek. Konkrétan, egy
komplex projektív egyenesek. Konkrétan, egy 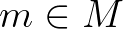 pont feletti fibrum a
pont feletti fibrum a 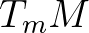 érintőtérnek a Riemann-metrikával kompatibilis komplex struktúráit paraméterezi. Ezáltal, valamint a Levi–Civita konnexiót felhasználva, a
érintőtérnek a Riemann-metrikával kompatibilis komplex struktúráit paraméterezi. Ezáltal, valamint a Levi–Civita konnexiót felhasználva, a 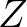 tvisztor-téren természetesen lehet értelmezni egy majdnem-komplex struktúrát. Penrose egy tétele értelmében ez a majdnem-komplex struktúra pontosan akkor integrálható (azaz, látja el
tvisztor-téren természetesen lehet értelmezni egy majdnem-komplex struktúrát. Penrose egy tétele értelmében ez a majdnem-komplex struktúra pontosan akkor integrálható (azaz, látja el 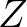 -t egy komplex analitikus sokaság-struktúrával), ha
-t egy komplex analitikus sokaság-struktúrával), ha 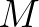 félig konformálisan lapos. Például, ha
félig konformálisan lapos. Például, ha 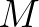 az
az 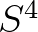 gömb az
gömb az  -ből örökölt kerek metrikájával, akkor tvisztor-tere megegyezik a
-ből örökölt kerek metrikájával, akkor tvisztor-tere megegyezik a 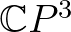 komplex projektív
komplex projektív 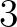 -dimenziós térrel; a
-dimenziós térrel; a 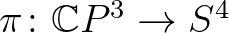 leképezés megértését az olvasóra bízzuk (segítség:
leképezés megértését az olvasóra bízzuk (segítség: 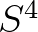 megegyezik a kvaternió-ferdetest feletti projektív egyenessel).
megegyezik a kvaternió-ferdetest feletti projektív egyenessel).
Ezen – elsőre meglehetősen bonyolultnak tűnő – konstrukciónak az az előnye, hogy bizonyos 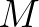 -en értelmezett, fizikailag releváns elliptikus parciális differenciálegyenletek (mezőegyenletek) megoldásainak terét ekvivalensen le lehet írni, mint bizonyos
-en értelmezett, fizikailag releváns elliptikus parciális differenciálegyenletek (mezőegyenletek) megoldásainak terét ekvivalensen le lehet írni, mint bizonyos 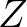 -n értelmezett holomorf objektumok terét. Mivel általában holomorf objektumok meghatározására számos módszer ismert (pl. kohomológia-terek kiszámolása), azért ezáltal érdekes differenciálegyenletek megoldásait ismert módszerekre vezethetjük vissza. Legegyszerűbb példája ilyen megfeleltetésnek az ún. Penrose-transzformált, amely bijekciót teremt bármely
-n értelmezett holomorf objektumok terét. Mivel általában holomorf objektumok meghatározására számos módszer ismert (pl. kohomológia-terek kiszámolása), azért ezáltal érdekes differenciálegyenletek megoldásait ismert módszerekre vezethetjük vissza. Legegyszerűbb példája ilyen megfeleltetésnek az ún. Penrose-transzformált, amely bijekciót teremt bármely 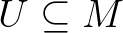 nyílt halmaz esetén a konform-invariáns hullámegyenlet
nyílt halmaz esetén a konform-invariáns hullámegyenlet  feletti megoldásai és a
feletti megoldásai és a 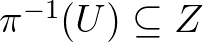 halmaz feletti bizonyos holomorf vonalnyaláb első kohomológia-csoportja között.
halmaz feletti bizonyos holomorf vonalnyaláb első kohomológia-csoportja között.
A tvisztor-tér alkalmazásokra talált egyéb területek mellett a differenciál- és integrálgeometriában, a csoport-ábrázolások elméletében, a fizikán belül pedig a kvantum-mezőelmélet szórási amplitudóinak kiszámításában.
Összegzés
Roger Penrose munkássága a felsoroltakon túlmenően kiterjed a (részben S. Hawking-gal közösen elért) szingularitási tételekre és az – azóta az általános relativitáselmélet egyik központi sejtésévé vált – kozmikus cenzor-hipotézisre. Ezekre a témákra e cikk folytatásában térünk ki.
Irodalomjegyzék
[1] https://www.nobelprize.org/prizes/economic-sciences/
[2] https://www.nobelprize.org/prizes/physics/2020/penrose/facts/
[3] https://ematlap.hu/tudomany-tortenet-2020-10/937-a-monge-kantorovics-problema
[4] H. S. M. Coxeter, A geometriák alapjai, Műszaki Könyvkiadó, 2. kiadás (1987).
[5] L. Penrose, R. Penrose, British Journal of Psychology, (Feb. 1958).
[6] R. Penrose, Twistor Algebra, Journal of Mathematical Physics 8 (1967) 345–366.
[7] R. Penrose, On the cohomology of impossible figures, Structural Topology 17 (1991), 11–16.
[8] R. Penrose, The role of aesthetics in pure and applied mathematical research, Bulletin of the Institute of Mathematics and Its Applications 10 (1974).
[9] R. Penrose, Twistor Theory after 25 years – its Physical status and prospects, in: London Mathematical Society Lecture Note Series 156 (1990), editors T. N. Bailey, R. J. Baston, 1–29.
[10] https://ematlap.hu/tudomany-tortenet-2020-12/998-stipsicz-titkos-conway-take2
[11] https://ematlap.hu/index.php/tudomany-tortenet-2018-06/688-hawking-matematikai-munkai
[12] https://en.wikipedia.org/wiki/Penrose_tiling









