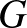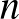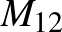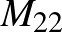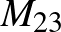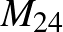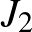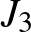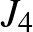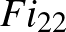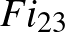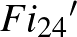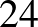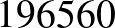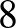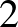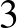A 2020-as évet beárnyékoló COVID-19 járvány a matematikus közösséget sem kímélte. A betegség szövődményeinek következtében április 11-én elhunyt John Horton Conway, a 20-ik század egyik legsokoldalúbb és legkülönlegesebb matematikusa. Ahogy hivatalos önéletrajzírója, Siobhan Roberts [9,10] fogalmazott, Conway a világ egyik legszerethetőbb egomániása, az egy személybe összegyúrt Arkhimédész, Mick Jagger, Salvador Dalí és Richard Feynman. A Brit Király Társaság néhai elnöke, Sir Michael Atiyah szerint pedig egyenesen a világ legmágikusabb matematikusa.
1. ábra. Simon J. Fraser karikatúrája Conwayről
Conway az angliai Liverpoolban született 1937-ben, egyetemi tanulmányait a Gonville and Caius College-ben folytatta Cambridge-ben. A doktori cím megszerzése után (1964) Ian Cassels segítségével a Sidney Sussex College-ban kapott állást. Cambridge-i évei alatt elnyerte a Berwick-díjat (1971) és tagjává választotta a Királyi Társaság (1981). Ez utóbbi kitüntetés kezdőbetűit (FRS, Fellow of the Royal Society) kiforgatva, gyakran viccelt azzal, hogy most már hivatalosan is egy „Mocskos Rohadt Disznó” (Filthy Rotten Swine). Öt évvel később, 1986-ban elfogadta a Princeton-i egyetem John von Neumann katedráját, ebben a pozícióban dolgozott egészen a 2013-as visszavonulásáig. Princetoni évei alatt elnyerte a Pólya-Díjat (1987), a Nemmers-Díjat (1998) és a Leroy P. Steele-Díjat (2000).
Conway matematikai munkássága annyira szerteágazó és mély, hogy ebben a cikkben kísérletet sem tehetünk annak teljes bemutatására. Szemléltetésképp kiválasztottunk három olyan egymástól meglehetősen távol eső területet, amelyen maradandót alkotott: csoportelmélet, sejtautomaták elmélete, csomóelmélet.
1. Conway-csoportok
A véges egyszerű csoportok klasszifikációja a huszadik század egyik legnagyobb matematikai programja volt. Az egyszerű csoportokat érintő problémák már a tizenkilencedik század végén is foglalkoztatták a csoportelmélettel foglalkozó matematikusokat, Otto Hölder 1892-ben ezt írta: „Es wäre von dem grössten Interesse, wenn eine Uebersicht der sämmtlichen einfachen Gruppen von einer endlichen Zahl von Operationen gegeben werden könnte.” (Nagyon érdekes lenne, ha véges számú művelet segítségével meg tudnánk adni az egyszerű csoportok teljes áttekintését.) Emlékeztetőül, egy csoport véges, ha véges sok eleme van, és egyszerű, ha a két triviálison kívül nincs másik normálosztója. Számtalan nagy eredmény született a huszadik század első felében, de a háborúk természetesen a matematikára is rányomták bélyegüket.
A második világháború végeztével a kutatások is új lendületet kaptak. Hans Zassenhaust idézve [1]: „Das interessanteste Problem scheint mir die Aufsuchung aller endlichen einfachen Gruppen zu sein.” (Számomra a legérdekesebb problémának a véges egyszerű csoportok klasszifikációja tűnik.) Az elkövetkező évtizedek bővelkedtek a mély eredményekben, többszáz cikk született a témában, összesen többtízezer oldalnyi bizonyítással, ezeknek a bemutatására itt természetesen nincs mód. Példaként említjük a huszadik század egyik matematikai csúcsteljesítményét, a klasszifikációhoz komoly technikai eszközöket adó Feit–Thompson tételt, amelynek bizonyítása a Pacific Journal of Mathematic egy teljes, több mint kétszázötven oldalas kötetét elfoglalta. Walter Feit és John G. Thompson tétele azt mondja, hogy minden páratlan rendű véges csoport feloldható, azaz van olyan normállánca, amelynek minden faktora kommutatív. Az érdeklődő olvasó rengeteget megtudhat a klasszifikáció történetéről Ronald Solomon „A Brief History of the Classification of the Finite Simple Groups” című cikkéből [8]. Mi most egészen 80-as évekig ugrunk előre, amikor úgy nézett ki, hogy a klasszifikáció teljes.
|
Véges egyszerű csoportok klasszifikációja. Legyen (a) (b) (c) (d) |
Ezt a tételt a klasszifikáció „első generációjának” nevezik, és mint arra utaltunk, ez sem adta könnyen magát. Megjegyzendő, hogy számtalan tisztázandó kérdés maradt, ami még évekig lekötötte a témával foglalkozó matematikusokat. Azért ennél a bizonyos első generációs tételnél álltunk meg, mert ebben kiemelkedő szerepe volt Conwaynek és szerzátársainak. Az „ATLAS of Finite Groups” című művükben megadták többek közt a sporadikus csoportok alapvető tulajdonságait (a csoportok rendjét, a külső automorfizmus-csoportjukat, különböző reprezentációikat, maximális részcsoportok konjugáltosztályait, és így tovább).

2. ábra. Conway és az ATLAS (Siobhan Roberts fotója)
Lépjünk vissza az időben: mint látható, a sporadikus csoportok közül három is Conway nevét viseli, de egyáltalán hogy került a doktoranduszként főleg számelmélettel és halmazelmélettel foglalkozó Conway a klasszifikáció közelébe? Conway híres volt a logikai játékokhoz fűződő, mindent háttérbe szorító szenvedélyéről. Ő maga úgy emlékszik vissza a hatvanas évekre, mint „a fekete ürességre”, vagy más szóval az állandó bűntudat éveire. Nyilvánvaló volt, hogy nagy dolgokra hivatott és sokat is várnak tőle, de a játékok okozta öröm és az eredménytelenség miatti szorongás váltakozása nem igazán segítette az áttörésben. Az 1966-os moszkvai nemzetközi matematikai kongresszuson aztán minden megváltozott. Egy John McKay nevű PhD hallgató a figyelmébe ajánlotta a Leech-hálót [6] mint objektumot, amelynek szimmetriáival érdemes lehet foglalkozni.
|
Gömbpakolások és a Leech-háló. Hogy mi is a Leech-háló, azt a legkönnyebben gömbpakolások segítségével lehet elmagyarázni. Egy gömbpakolásokhoz kapcsolódó kérdés az, hogy az
3. ábra. Conway rajza az optimális gömbpakolásról és a középpontok által megadott hálóról. Rejtélyes módon ez a bizonyos kissing number csak néhány speciális dimenzióban ismert, ezek: |
Látva a Leech-háló misztikus tulajdonságait, elhatározta, hogy megvizsgálja a szimmetriát: szerdánként hattól éjfélig, szombatonként pedig déltől éjfélig még a családnak is tilos zavarni (hónapokon keresztül, ha kell), akkor ugyanis csak erre a problémára fókuszál! Legnagyobb meglepetésére gyakorlatilag az első ilyen alkalommal megtörte a problémát. A Leech-hálónak 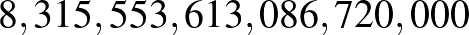 szimmetriája van, jelölje a szimmetriák csoportját
szimmetriája van, jelölje a szimmetriák csoportját  . A centrumával kifaktorizálva egy olyan véges egyszerű csoportot kapott, amely akkoriban még ismeretlen volt, ez a
. A centrumával kifaktorizálva egy olyan véges egyszerű csoportot kapott, amely akkoriban még ismeretlen volt, ez a 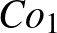 -gyel jelölt Conway-csoport, amelynek rendje
-gyel jelölt Conway-csoport, amelynek rendje 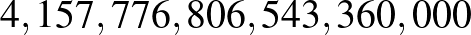 . Talált két másik, addig ismeretlen véges egyszerű csoportot is, ezek izomorfak a
. Talált két másik, addig ismeretlen véges egyszerű csoportot is, ezek izomorfak a 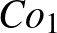 egy-egy részcsoportjával. A
egy-egy részcsoportjával. A 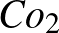 elemszáma
elemszáma 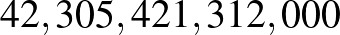 , a
, a 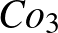 -é
-é  .
.
Ez az áttörés nemcsak a világhírt hozta meg számára, de a bűntudatát is szertefoszlatta. Úgy gondolta, hogy ezek után nem kell a sikertelenség terhét cipelnie, és rosszul éreznie magát amiatt, hogy olyan (néha érdektelennek tűnő) játékokon vagy problémákon gondolkozik, amelyekben örömét leli.
2. Életjáték
Conway egyik leghíresebb agyszüleménye, amely a matematikus társadalmon kívül is ismertté tette, az 1970-ben felfedezett Életjáték nevű „sejtautomata”. Hasonló (bár némileg bonyolultabb) automaták létrehozásán dolgozott Los Alamosban Neumann János és Stanislaw Mazur is, tehát a játékot jelentéktelennek nevezni semmiképp nem lehet. Sőt, az Életjáték megreformálta az automaták egész elméletét. Ugyanakkor talán túlságosan is rányomta a bélyegét Conway munkásságára, legalábbis abban az értelemben, hogy a világ azzal, nem pedig a valóban mély matematikai eredményeivel társította a nevét. Ő maga a kétezres években már nem is szívesen beszélt a játékról.

4. ábra. Conway az Életjátékkal játszik. Fotó: Kelvin Brodie/the Sun
|
Az Életjáték szabályai. Egy végtelen négyzetrácson játszunk, a négyzeteket celláknak nevezzük. A játék kezdetén eldönthetjük (és ez az egyetlen alkalom, hogy bármilyen hatásunk van a játékra), hogy mely cellákba teszünk élő sejtet. Egy sejtnek két állapota van: élő vagy élettelen. Egy cella környezete alatt az őt közvetlenül körülvevő (1) Minden olyan élő sejt, amelynek (2) Egy élő sejt elpusztul, ha kettőnél kevesebb (elszigetelődés), vagy háromnál több (túlnépesedés) élő sejt van a környezetében. (3) Új élő sejt születik minden olyan cellában, amelynek környezetében pontosan három élő sejt található. Fontos, hogy az elhaló sejtek az adott lépésben nem akadályozzák a születést és a túlélést, és a születések nem mentik meg az a szabály szerint elhalásra ítélteket. |
Nézzünk egy egyszerű példát: a játékot 8 (2 x 4-es téglalapba elrendezett) élő sejttel elindítva egy lépésben egyensúlyi állapotba jutunk. Tehát rögtön látunk egy olyan játékot, amely véges sok lépésben véget ér, és aminek a vége nem a teljes kipusztulás. A végén minden élő sejtnek pontosan két élő szomszédja van, tehát életben marad, és nem jönnek létre új élő sejtek.
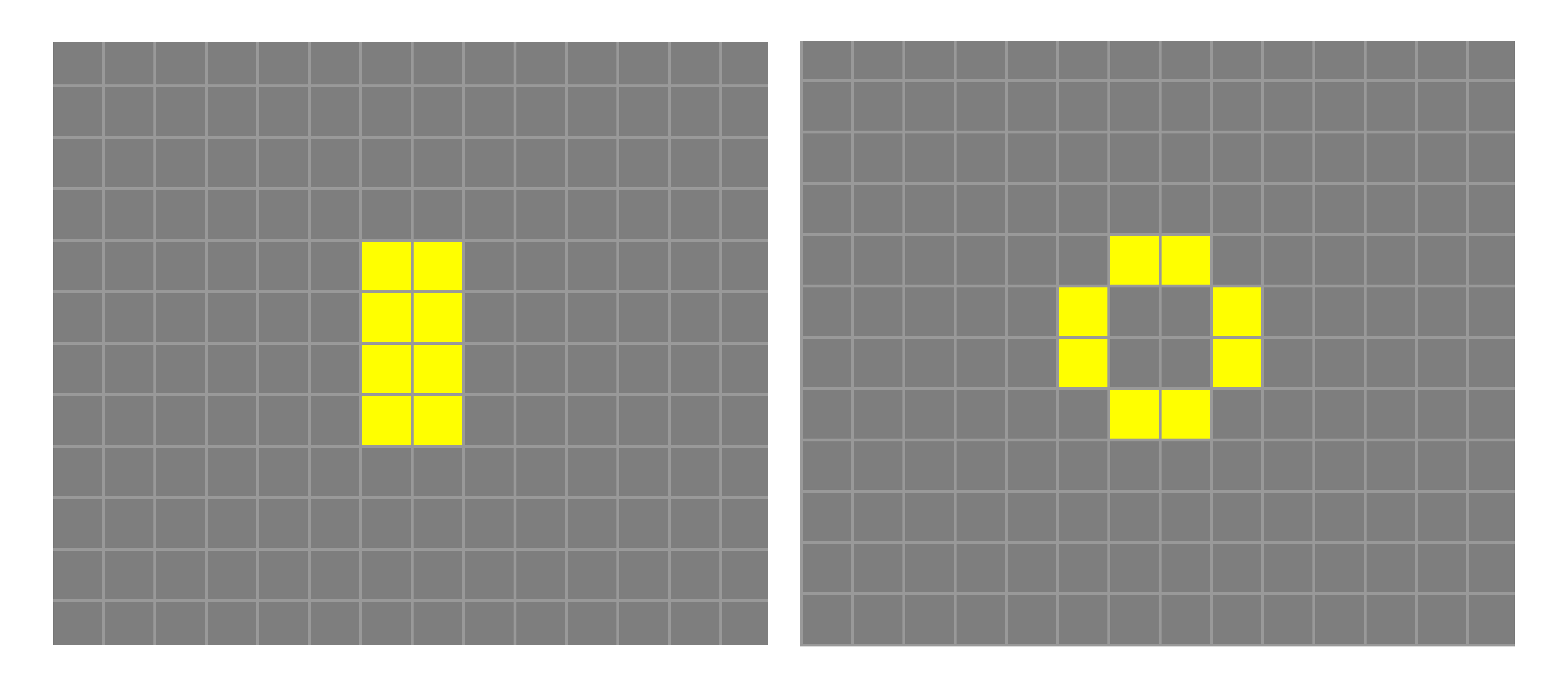
Ezzel szemben ha a fenti kezdeti állaptot megbolygatjuk, és két további élő sejtet hozzáadunk, akkor egy olyan 2 x 5-ös populációt kapunk, amelyik a tizedik lépésben kihal.

Világos, hogy az utolsó képen látható élő sejtek mind elhalnak, és nem jön létre új élő sejt. A játékot ki lehet próbálni a https://playgameoflife.com/ oldalon. Számtalan kérdés merül fel az emberben: Milyen mozdulatlan alakzatok vannak? Van-e olyan alakzat, amelyik pulzál, azaz azonos időközönként (periodikusan) visszatér a kezdeti állapotába? Van-e olyan alakzat, amely néhány lépés után hasonló alakba tér vissza, de közben elmozdul?
Némi gondolkodás és próbálkozás után mindenki maga megválaszolhatja a ezeket a kérdéseket. A játék angol nyelvű https://en.wikipedia.org/wiki/Conway%27s_Game_of_Life Wikipédia-oldalán egyébként egy elég széleskörű gyűjtés található ezekből a konstrukciókból.
3. Csomóelmélet
Bár John Conway kevés számú csomóelméleti cikket írt (és azok többsége is jó pár évtizede jelent meg), hatása a csomóelméleti kutatásokra megkerülhetetlen. A legenda szerint egész fiatalon újra felfedezte a bogozási relációnak (skein relation) nevezett összefüggést bizonyos, egymásból megkonstruálható csomók Alexander-polinomjára.
Alexander 1928-ban jelentette meg munkáját, amelyben egy 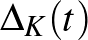 polinomot (pontosabban Laurent-polinomot, tehát negatív egész kitevőket is megengedő „polinomot”) rendel minden
polinomot (pontosabban Laurent-polinomot, tehát negatív egész kitevőket is megengedő „polinomot”) rendel minden  csomóhoz, annak síkba vett vetülete alapján, könnyebbé téve csomók megkülönböztetését. A
csomóhoz, annak síkba vett vetülete alapján, könnyebbé téve csomók megkülönböztetését. A 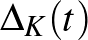 polinom kiszámítása azonban általában nem egyszerű. Vegyük a
polinom kiszámítása azonban általában nem egyszerű. Vegyük a  csomó (ami definíció szerint a körvonal egy beágyazása a háromdimenziós térbe) egy síkra vett általános, tehát csak kettős pontokat tartalmazó vetületét. Egy tetszőlegesen kiválasztott kettőspontnál három műveletet végezhetünk:
csomó (ami definíció szerint a körvonal egy beágyazása a háromdimenziós térbe) egy síkra vett általános, tehát csak kettős pontokat tartalmazó vetületét. Egy tetszőlegesen kiválasztott kettőspontnál három műveletet végezhetünk:
– nem változtatunk meg semmit
– felcseréljük a felül és alul menő íveket
– eltöröljük a kettőspontot.
(Ez utóbbira két lehetőségünk is van; ha azonban választunk a csomón egy irányítást, akkor a kereszteződést vagy az alábbi ábra bal, vagy középső rajza fogja leírni, és az általunk választott eltörlést mutassa a jobb oldali rajz.)
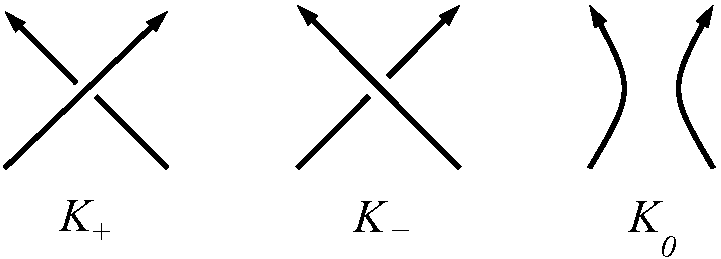
5. ábra. A bogozási relációban résztvevő három lánc mindenhol megegyezik, kivéve egy kis körlapot, azon belül pedig a fenti három ábra mutatja viselkedésüket.
A bogozási reláció szerint a kapott, rendre 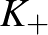 -szal,
-szal, 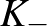 -szal és
-szal és 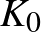 -lal jelölt csomók közül az eredeti csomó vagy
-lal jelölt csomók közül az eredeti csomó vagy 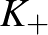 vagy
vagy 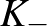 , attól függően, hogy milyen típusú kereszteződést választottunk a bogozási reláció alkalmazásának kezdetekor, és
, attól függően, hogy milyen típusú kereszteződést választottunk a bogozási reláció alkalmazásának kezdetekor, és 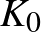 valójában már nem is csomó lesz, hanem lánc, vagyis két komponensű csomó. Ezen csomók (és láncok) Alexander-polinomjai a bogozási reláció szerint a következő azonosságot teljesítik:
valójában már nem is csomó lesz, hanem lánc, vagyis két komponensű csomó. Ezen csomók (és láncok) Alexander-polinomjai a bogozási reláció szerint a következő azonosságot teljesítik:
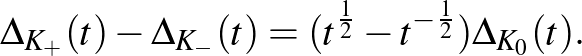
Valójában ez az összefüggés a 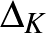 Alexander-polinom definíciójaként is szolgálhat (azzal a további, normalizáló feltevéssel, hogy az
Alexander-polinom definíciójaként is szolgálhat (azzal a további, normalizáló feltevéssel, hogy az  triviális csomóra
triviális csomóra 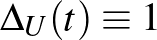 ). Ehhez pusztán azt kell meggondolni, hogy a kereszteződés alkalmas választásával a két újonnan keletkezett csomó/lánc valamilyen értelemben „egyszerűbb'' mint a kezdő csomó. (Mégsem szokták evvel a tulajdonsággal definiálni
). Ehhez pusztán azt kell meggondolni, hogy a kereszteződés alkalmas választásával a két újonnan keletkezett csomó/lánc valamilyen értelemben „egyszerűbb'' mint a kezdő csomó. (Mégsem szokták evvel a tulajdonsággal definiálni 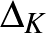 -t, mert a számításnak a választott kereszteződéstől való függetlensége egyáltalán nem egyszerű.)
-t, mert a számításnak a választott kereszteződéstől való függetlensége egyáltalán nem egyszerű.)
Conway valójában meg is változtatta az Alexander-polinom megjelenítését, és egy alkalmas helyettesítéssel a 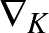 Alexander–Conway-polinomot definiálta, amelyre a sokkal egyszerűbb
Alexander–Conway-polinomot definiálta, amelyre a sokkal egyszerűbb
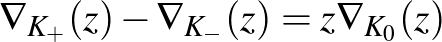
csomóinvariánst adta. ( -t a
-t a 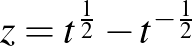 helyettesítés adja
helyettesítés adja 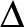 -ból.)
-ból.)
Conway egy másik észrevétele volt, hogy mutáció során a polinominvariánsok nem változnak. Mutáció során a diagramban egy körlapot keresünk, amelynek pereme a csomó diagramját 4 pontban metszi, a körlapot kivágjuk, majd 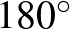 -os forgatás után visszatesszük. E művelet egy példáját mutatja az alábbi rajz.
-os forgatás után visszatesszük. E művelet egy példáját mutatja az alábbi rajz.
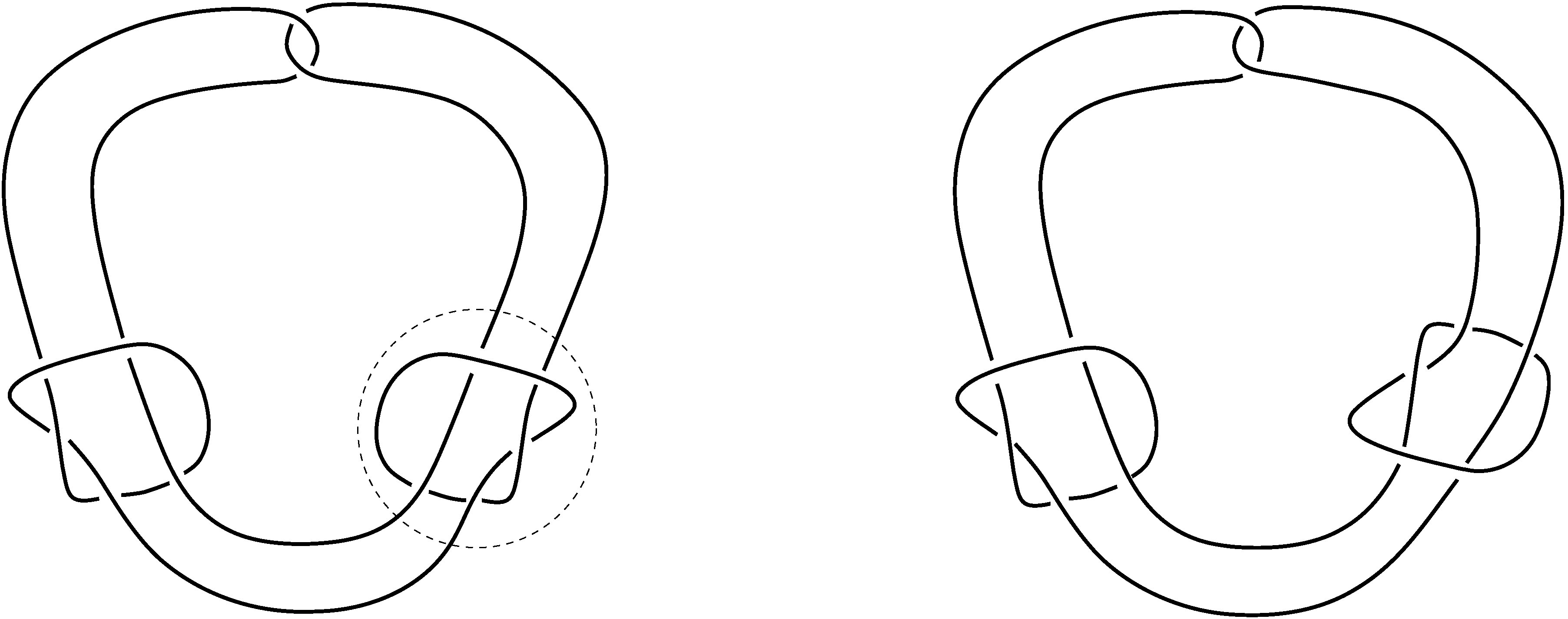
6. ábra. A  Kinoshita–Terasaka-csomó (balra) és a
Kinoshita–Terasaka-csomó (balra) és a  Conway-csomó (jobbra). A két csomó egymás mutánsa.
Conway-csomó (jobbra). A két csomó egymás mutánsa.
A bal oldali csomót Kinoshita és Terasaka fedezte fel, és avval a tulajdonsággal bír, hogy bár nem a triviális csomó, de Alexander-polinomja megegyezik a triviális csomó Alexander-polinomjával. A jobb oldali csomót pedig Conway-csomónak nevezzük.
Ugyan a Kinoshita–Terasaka-csomó nem triviális, valamilyen távoli rokonságban van a triviális csomóval. Könnyű látni, hogy csak a triviális csomó rendelkezik avval a tulajdonsággal, hogy egy háromdimenziós térbe beágyazott körlap pereme. Mi a helyzet azonban, ha a háromdimenziós terünket a négydimenziós (alsó) féltér peremeként tekintjük, és a körlapoknak megengedjük, hogy belsejük a negyedik dimenzióba menjen? Ekkor sokkal több csomó fog (ilyen általánosabb) körlapot határolni – például a Kinoshita–Terasaka-csomó is. Ez az állítás nem kézenfekvő, de nem is olyan nehéz belátni; azon múlik, hogy ezt a csomót elő tudjuk-e úgy állítani, hogy két triviális csomóhoz egy szalagot ragasztunk.
A kérdés, ami számos topológust foglalkoztatott évtizedeken át, hogy a mutáció során ez a tulajdonság megmarad vagy elveszik. Még konkrétabban: a Conway-csomó határol-e a négydimenziós térbe (simán) beágyazott körlapot? (Egy terminus technicusszal élve: metszet csomó-e a Conway-csomó?)
A kérdésre a választ 2018-ban nagy meglepetésre egy (kiemelkedően tehetséges) végzős doktorandusz, Lisa Piccirillo a texasi UT Austin egyetemről találta meg: a Conway-csomó nem metszet, nem határol a negyedik dimenzióba simán beágyazott körlapot [7]. Következésképp a Conway-mutáció meg tudja változtatni ezt a tulajdonságot.
A cikket néhány érdekes videóval zárjuk:
– Conway frappáns bizonyítása csomók kicsomózhatatlanságáról (további részletek itt).
– Conway (többek közt) a Monster csoportról beszél.
– Conway az Életjáték feltalálásáról mesél.
– Siobhan Roberts és John Conway beszélget.
Irodalomjegyzék
- [1] H. Bender, Entwicklungslinien in der Theorie endlicher Gruppen, Jber. d. Dt. Math.-Verein. (1992), 77–123.
[2] A. Connes és J. Kouneiher, Sir Michael Atiyah, a Knight Mathematician A Tribute to Michael Atiyah, an Inspiration and a Friend, Notices Of The American Mathematical Society Volume 66, Number 10 p.1660, 2019.
[3] J. H. Conway, R. T. Curtis, S. P. Norton, R. A. Parker, R. A. Wilson, Atlas of Finite Groups: Maximal Subgroups and Ordinary Characters for Simple Groups, Oxford University Press, ISBN 978-0-19-853199-9 (1985).
[4] J. H. Conway, N. J. A. Sloane, Sphere Packings, Lattices and Groups, Series: Grundlehren der mathematischen Wissenschaften 290 Publisher: Springer New York, 1988.
[5] O. Hölder, Die einfachen Gruppen in ersten und zweiten Hundert der Ordnungszahlen, Math. Annalen 40 (1892), 55–88.
[6] J. Leech, Some sphere packings in higher space, Can. J. Math., 16 (1964), 657–682.
[7] L. Piccirillo, The Conway knot is not slice, Annals of Mathematics, 191(2), 581–591.
[8] R. Solomon, A Brief History of the Classification of the Finite Simple Groups, Bull. Amer. Math. Soc., 38(3):315–352, 2001.
[9] S. Roberts, Genius at Play: The Curious Mind of John Horton Conway, Bloomsbury USA, 2015, 480 pages, ISBN-13: 978-1620405932.
[10] S. Roberts, John Horton Conway: the world's most charismatic mathematician, The Guardian
A cikk az ITM és az NKFIH ÚNKP-20-5-BGE-1 és PD128374 kódszámú projektjeinek, valamint az MTA Bolyai János Kutatási Ösztöndíjának támogatásával készült.