Szintfelmérés a Miskolci Egyetemen

Bejövő hallgatók matematikai szintfelmérése a Miskolci Egyetemen

Bevezető

A tapasztalatok azt mutatják, hogy a felsőoktatásba jelentkező hallgatók matematikatudása jelentős mértékben differenciált. Ennek egyik oka, hogy a hallgatók különböző típusú középiskolákból érkeznek, ahol eltérő tantervekkel és tanítási módszerekkel találkozhattak. Előfordul, hogy bizonyos típusú szakközépiskolákból érkező hallgatóknak előnyt jelent a már tanult szakrajz, géprajz néhány egyetemi tantárgynál (például Ábrázoló geometriánál), de esetükben sokszor az figyelhető meg, hogy nehezebben megy a matematikai tudásra épülő tantárgyak befogadása, mint például az Analízis vagy a Lineáris algebra, hiszen középiskolájukban alacsonyabb óraszámban tanulták a matematikát. A különbségeket tovább mélyíti, hogy a műszaki, illetve informatikai szakokra való bekerüléshez nem feltétlenül szükséges matematikából emelt szintű érettségit tenni. A szilárd alapok hiánya megnehezíti az egyetemi szintű matematika tananyag elsajátítását, a sikeres előrehaladást. Ezért kiemelten fontos, hogy már az elején azonosítsuk a hiányosságokat, és szükség esetén időben, hatékony támogatást nyújtsunk a hallgatóknak. Ezt a célt szolgálja a bejövő hallgatók matematikai kompetenciamérése.

A szintfelmérésnek a Miskolci Egyetem Gépészmérnöki és Informatikai Karán (GÉIK) és annak jogelődjén már a korábbi évtizedekben is volt gyakorlata. 2022 szeptemberében azonban a mérést a társkarokra is kiterjesztettük, azaz az ME minden olyan elsőéves alapképzési szakos hallgatójára, akinek valamilyen matematikatárgy szerepel a mintatantervében. A 2022/2023. tanév 1. félévében a Miskolci Egyetem informatikai, műszaki, illetve gazdaságtudományi területéhez tartozó I. éves BSc szakos hallgatóinak körében végzett matematikai kompetenciamérés eredményeinek elemzését egy korábbi cikkünkben ([1]) már megtettük.

2023 szeptemberében új koncepció szerint bonyolítottuk le a szintmérést és a kapcsolódó felzárkóztatást. A GÉIK belépő hallgatóinak mérése a regisztrációs hét első napján megtörtént. A tesztet a hallgatók az egyetemi e-learning-rendszerben írták meg, a nappali tagozatos hallgatók személyes jelenléttel, a levelező munkarendben tanulók online módon. A 2023/2024-es tanévtől a kar alapképzési (BSc) szakos mintatanterveinek első félévére Matematikai kompetenciafejlesztő kurzus címmel 0 kredites (kötelező) kritériumtárgy került beillesztésre. A fejlesztés célja a hallgatók tanterv szerinti előmenetelének segítése, a későbbi esetleges lemorzsolódás megelőzése. A felmérő eredményes teljesítése esetén a Matematikai kompetenciafejlesztő kurzus című tárgyat elismertként fogadjuk el, a hallgatók a félév elején megkapják az aláírást. A belépési szintfelmérőt sikertelenül teljesítők, illetve meg nem írók részére szükséges a kompetenciafejlesztő kurzus elvégzése. Ebben a tanévben vezettük be, hogy a felzárkóztató foglalkozásokat a nappali tagozatos hallgatóknak – a mérést követő nappal kezdődően – a regisztrációs héten tömbösített formában tartjuk, ezzel is támogatva a tanév sikeres megkezdését. Az órákat videófelvételen rögzítettük, amelyet az összefoglaló tananyagokkal, gyakorló feladatokkal együtt a szorgalmi időszak első hetének végéig az egyetemi zárt e-learning-rendszerben található, minden érintett hallgató által elérhető felzárkóztató kurzushoz feltöltöttük. Az online tananyagok, visszanézhető felvételek így azon (pl. levelező tagozatos) hallgatók számára is támogatást nyújtanak, akik nem tudnak részt venni a felzárkóztató foglalkozásokon.

Az érettségi témakörei

A 2005-ben bevezetett kétszintű érettségi rendszerrel párhuzamosan megszűntek a felsőoktatásba bekerüléshez szükséges felvételi vizsgák. Az eredeti koncepció értelmében az emelt szintű érettségi a felsőoktatási intézményekbe való jelentkezés feltétele lett volna, míg a középszintű érettségi a középfokú tanulmányok lezárására lett volna hivatott. Ez az elképzelés azonban nem vált valóra [2]. Ugyan 2020-tól bevezetésre került, hogy minden képzési területen felvételi követelmény az emelt szintű érettségi, de még a műszaki és informatikai képzési terület szakjain sem volt kötelező azt matematikából teljesíteni. 2023-tól újabb átalakuláson ment át a felvételi rendszer, intézményi hatáskörbe került annak eldöntése, hogy előírják-e felvételi követelményként az emelt szintű érettségi vizsgát. Így a Miskolci Egyetem szakjainak többségén – a 2023-as általános felvételi eljárástól kezdődően – elegendő a középszintű érettségi megléte.

Az Érintő egy ötrészes cikksorozatában Csapodi Csaba bemutatja, hogy a 2020-ban bevezetett új Nemzeti alaptanterv és az ehhez tartozó kerettanterv változásai 2024-től hogyan módosítják a matematika érettségi követelményeket. Az érettségi rendszer változásait, témakörönként és szintenként, táblázatos formában részletezve, áttekinthető módon adja meg (pl. [3], [4]), így cikkünkben csak érintőlegesen térünk ki a változásokra.

A középszintű érettségi témakörei a matematika alábbi fejezeteiből kerülnek ki:

1. Gondolkodási módszerek, halmazok, logika, kombinatorika, gráfok

2. Számelmélet, algebra

3. Függvények, az analízis elemei

4. Geometria, koordinátageometria, trigonometria

5. Valószínűségszámítás, statisztika

A 2023/2024-es tanévben felvett hallgatók az előző NAT alapján meghatározott vizsgakövetelmények szerint érettségiztek, sőt számos levelező tagozatos hallgató még a kétszintű érettségi bevezetése előtt vizsgázott. Így egyidejűleg figyelembe kell vennünk a korábbi érettségi követelményeket, illetve fel kell készülnünk a matematika tantárgy új NAT szerinti tartalmi változásaira. Több, elsősorban a műszaki, illetve informatikai, alapképzési szakok szempontjából releváns témakör a középszintű érettségi vizsga követelményei közül átkerült az emelt szintű követelmények közé, vagy kikerült a középiskolai kötelező tananyagból [5].

A műszaki és informatikai BSc szakok esetén a kötelezően teljesítendő tárgyak között szerepel általában két féléven keresztül analízis témakörű kurzus, legalább egy félévben lineáris algebra, illetve diszkrét matematika. A gazdaságtudományi területhez tartozó BSc szakok esetén a két féléves matematikai tárgyak tematikája az analízis, a valószínűségszámítás, alkalmazott lineáris algebra és az operációkutatás elemeit öleli fel. A legtöbb hallgató számára ezek az alapozó jellegű matematikakurzusok nehezen teljesíthetőek, hiszen jelentős mennyiségű új ismeret elsajátításáról kell számot adniuk, valamint a sikeres abszolváláshoz elengedhetetlenül szükségesek a középiskolában szerzett jó matematikai alapok. Ezek hiányában a hallgatók lényegesen nehezebben tudják megoldani a zárthelyi dolgozatokban, illetve a vizsgadolgozatokban kitűzött feladatokat. A hézagos matematikai tudásanyaggal érkező hallgatóknak a kurzusok sikeres teljesítéséhez nemcsak az új anyagot kell elsajátítaniuk, hanem pótolniuk kell a középiskolai anyag megfelelő fejezeteit is. Ezért indokolt már az egyetemi tanulmányok megkezdésekor a felvételt nyert hallgatók bemeneti matematikai kompetenciájának mérése, hogy szükség esetén megtörténjen a beavatkozás, a szintre hozás, így elkerülve a későbbi esetleges lemorzsolódást.

A matematikai szintfelmérésről

A bejövő hallgatók matematikai szintfelmérését összesen 1126 elsőéves műszaki, informatikai, illetve gazdaságtudományi képzési területhez tartozó BSc-s (672 nappali, illetve 454 levelező tagozatos) hallgató írta meg. A karonkénti létszámadatok a következő ábrán láthatók:

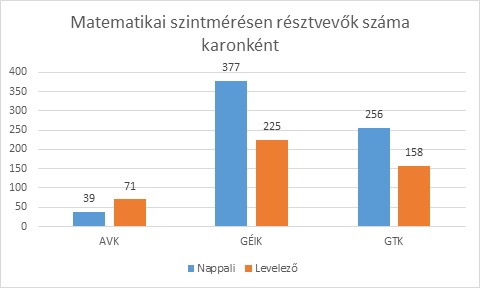
1. ábra Szintmérésen résztvevők száma karonként és tagozatonként

A bevezetőben is említettük, hogy a Gépészmérnöki és Informatikai Kar (GÉIK) újonnan felvett alapképzési szakos hallgatóinak a regisztrációs hét első napjára ütemeztük a matematikai felmérő tesztet. A regisztrációs hét második felében írták meg a szintmérést az Anyag- és Vegyészmérnöki Kar (AVK) érintett hallgatói, a Gazdaságtudományi Kar (GTK) elsőéves BSc-s hallgatói pedig a szorgalmi időszak megkezdése után vettek részt a szintmérésen.

A teszt megírására 45 perc állt rendelkezésre, a feladatsor 15 feleletválasztós kérdést tartalmazott, amelyeket a matematika középszintű érettségi témaköreihez kapcsolódóan válogattunk. A diákok öt lehetőségből választhattak egyet. Minden jó válasz 4 pontot ért, a hibás válasz 1 pont levonásával járt, míg a nem megválaszolt feladatra nem adtunk pontot.

A feladatokat igyekeztünk úgy összeállítani, hogy az egyetemi tananyag elsajátítása szempontjából fontos témakört érintsenek és reális képet kapjunk a diákok megfelelő ismereteiről, hiányosságaikról. A szintmérés előtt a hallgatók számára közzétettünk gyakorló feladatsort, illetve tájékoztattuk őket a belépési szintfelmérő céljáról és tematikájáról. A műszaki és informatikai képzési terület esetén a középiskolai matematikai tananyagból az alábbi témákat emeltük ki:

$\mathrm{\checkmark}$ műveletek, algebrai átalakítások

$\mathrm{\checkmark}$ hatványozás, gyökvonás, logaritmus azonosságai

$\mathrm{\checkmark}$ egyenletek, egyenlőtlenségek: elsőfokú, másodfokú, törtes, gyökös, abszolútértékes, exponenciális, logaritmusos, trigonometrikus

$\mathrm{\checkmark}$ egyenletrendszerek

$\mathrm{\checkmark}$ elemi függvények, függvénytranszformációk, függvények tulajdonságai

$\mathrm{\checkmark}$ sorozatok

$\mathrm{\checkmark}$ elemi síkgeometria, elemi térgeometria

$\mathrm{\checkmark}$ vektorok, koordinátageometria

$\mathrm{\checkmark}$ trigonometria

A GTK hallgatói számára a Gazdasági matematika 1. tárgyhoz a középiskolában tanult kombinatorikai alapismeretek is szükségesek, így esetükben a kevésbé releváns geometriai témakörű feladatok helyett kombinatorikai kérdések szerepeltek. Továbbá hangsúlyosabban megjelentek a sorozatokkal (mértani sorozat, kamatos kamat) kapcsolatos feladatok.

Az elérhető 60 pontból a hallgatók átlagosan 25,5 pontot teljesítettek, a szórás 16,1 volt, amely megerősíti a bevezetőben is említett heterogén alaptudást. A maximális 60 pontot (az 1126 résztvevőből) 20 hallgató érte el. A tesztet akkor tekintettük sikeresnek, ha az eredmény minimum 24 pont volt. A belépési szintmérőt sikeresen teljesítő 611 hallgatónak a Matematikai kompetenciafejlesztő kurzus c. tárgyat elismertként fogadtuk el.

A következő ábrákon karonként adjuk meg az elért pontszámok eloszlását. Az eredmények megfelelnek a 2023-as felvételi pontszámok alapján előzetesen vártaknak. Egyrészt a korábbi évekhez képest alacsonyabb pontszámmal is be lehetett kerülni képzéseinkre, másrészt a gazdaságtudományi szakok esetén a ponthatár magasabb volt, mint a műszaki és informatikai képzési terület szakjainál. Tovább árnyalhatja az átlagok közötti különbséget a szintfelmérés – előzőekben már említett – karonként eltérő ütemezése. A GTK hallgatói a szorgalmi időszakban írták meg a tesztet, amikor a felzárkóztató kurzus tananyagai a zárt e-learning-rendszerben már rendelkezésre álltak.

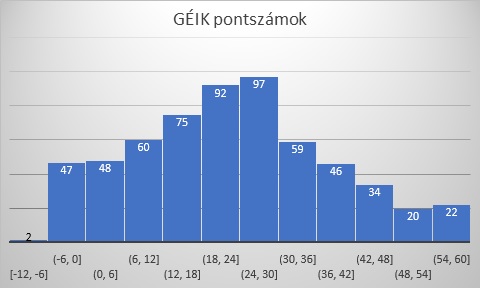
2. ábra A Gépészmérnöki és Informatikai Kar bejövő BSc-s hallgatóinak a szintmérésen elért pontszámainak a hisztogramja

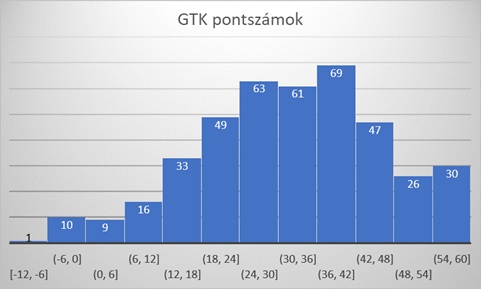
3. ábra A Gazdaságtudományi Kar bejövő BSc-s hallgatóinak a szintmérésen elért pontszámainak a hisztogramja

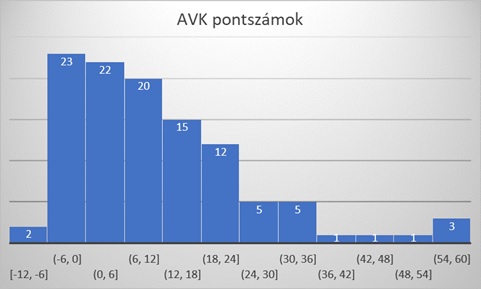
4. ábra Az Anyag- és Vegyészmérnöki Kar bejövő BSc-s hallgatóinak a szintmérésen elért pontszámainak a hisztogramja

A feladatok elemzése

A továbbiakban a Gépészmérnöki és Informatikai Kar nappali tagozatos hallgatóinak eredményét elemezzük, a 377 fő által megírt bemeneti kompetenciamérés eredményeit alapul véve.

A tesztben egy számtani sorozattal kapcsolatos egyszerűbb feladatot és egy kétismeretlenes egyenletrendszert sikerült a legtöbb hallgatónak megoldani.

A két feladat a következő volt:

Egy számtani sorozat második eleme 12, negyedik eleme 18. Mennyi az első 10 elem összege?
Oldja meg a következő egyenletrendszert:

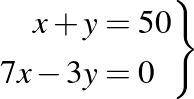
$\displaystyle \left.\begin{aligned} x+y&=50\\ 7x-3y&=0\end{aligned}\right\}$

Mennyi lesz az egyenletrendszer megoldásainak szorzata?

A 377 főből 329 fő tudott jó választ adni a számtani sorozatos feladatra, ami 87,27%-os arány. A 2022 szeptemberében megíratott kompetencia teszt esetén szintén az egyik legsikeresebben teljesített példa a sorozatos feladat volt. Ezek alapján megállapítható, hogy a sorozatokkal kapcsolatos egyszerűbb feladat megoldása nem jelent különösebb problémát a hallgatóknak.

Az egyenletrendszeres feladat esetében a jó megoldások száma 274 volt, ami 72,68%-os arányt jelent. Az egyetemi tananyagban lineáris algebrában, vagy analízisben például a racionális törtfüggvények integrálásnál is használniuk kell majd az egyenletrendszerek megoldására vonatkozó ismereteiket.

A harmadik legjobban sikerült feladat a másodfokú egyenletek témakörébe tartozott:

Mennyi az 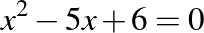egyenlet valós megoldásainak a négyzetösszege?

Erre a feladatra a 377 diákból 255-en válaszoltak helyesen, ami 67,64%-os arányt jelent. Itt azért már érezhető a csökkenés mértéke az első feladat 87,27%-hoz képest, pedig egy egyszerű, két egész megoldással rendelkező másodfokú egyenletet adtunk meg. Azt nem tudjuk a válaszokból lemérni, hogy a másodfokú egyenletet jól oldotta-e meg, csak a gyökök négyzetösszegét határozta meg esetleg rosszul.

A problémás feladatok elemzése

A feladatok közül a legkevésbé egy logaritmusfüggvény értelmezési tartományára vonatkozó, 13. feladat feladat sikerült.

Mi a valós számok halmazának az a legbővebb részhalmaza, ahol az 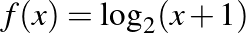$f(x)=\log_2(x+1)$ függvény értelmezhető?

A 378 válaszadóból csak 155 fő oldotta meg helyesen a feladatot. Ez a válaszadók 41%-os arányát jelenti, azaz a diákoknak kevesebb mint a felét. Tapasztalataink is alátámasztják a fenti eredményt, ugyanis az elsőéves hallgatók körében a függvények témakörében jelentkeznek a legnagyobb hiányosságok. Ugyanakkor az első félévben teljesítendő analízis kurzusok egyik legfontosabb fejezete az egyváltozós valós függvények elméletéhez kapcsolódik, így a sikeres vizsga szempontjából elengedhetetlen a középiskolában korábban megismert (az első és másodfokú, az abszolútérték, a négyzetgyök, a trigonometrikus, az exponenciális és logaritmus) függvények egzakt ismerete [5]. A korábban említett változások miatt pl. a logaritmusfüggvény ábrázolása és jellemzése is kikerült a 2020-as NAT szerint a középszintű követelményekből, illetve a logaritmus azonosságai sem tartoznak a kötelező anyagrészek közé. Ugyanez elmondható a trigonometrikus függvények témaköréről. Az emelt szintű tananyagnak természetesen része a fent említett összefüggések és a függvények ábrázolása is, amelyről bővebben olvashatunk Csapodi Csaba erre vonatkozó cikkében [3]. Azonban kevesen rendelkeznek emelt szintű érettségivel matematikából, miközben az egyetemi oktatásban szükség van a fenti témakörökre. Ezért az egyetemi oktató kollégák számára kiemelten fontos, hogy hangsúlyt helyezzenek ezen ismeretek megfelelő átadására, és ne tekintsék ezeket magától értetődőnek.

Sajnos még rosszabb eredményt értek el a diákok a következő feladat esetében:

Az a paraméter mely értéke esetén párhuzamo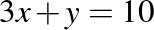s a

és a

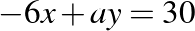egyenes?

A 377 diákból 62 fő tudott erre a kérdésre helyesen válaszolni, ami 16,45%-os arány. A teszt ezen eredménye is visszaigazolta azt, hogy a koordinátageometria sok esetben nehézséget jelent. Ennek egyik oka az lehet, hogy ahhoz, hogy valaki jó legyen ebben a témában, biztos geometriai és algebrai alapokkal is rendelkeznie kellene. A középiskolai koordinátageometriai ismeretekre szükség van az Analízis tárgyak esetén, de említhetnénk a Lineáris algebra tárgy vektorokkal foglalkozó fejezetét is, ahol szintén ezekre az ismeretekre építünk. A függvényeknél már említetteknek megfelelően a jövőben itt is figyelembe kell venni, hogy a középszintű tananyagból mely témakörök (pl. a skaláris szorzat definíciója, tulajdonságai) maradtak ki, kerültek át az emelt szintre [4].

Konklúzió

A kompetenciamérés eredménye megerősítette az egyetemi matematikaoktatás során szerzett tapasztalatainkat. A frissen felvett hallgatók azokban a feladatokban bizonyultak kevésbé eredményesnek, amelyek nehézségére előzetesen számítottunk. A teszt összeállításakor az volt a célunk, hogy szinte az összes releváns témakört lefedjük, a jelenléti megíratással pedig arra törekedtünk, hogy a valós tudásukról kapjunk képet. A teszt írása során a feladatokat feleletválasztós kérdések formájában kellett megoldani, de a nehézségeket jelentő témakörök esetén a felkínált válaszlehetőségek sem mindig nyújtottak megfelelő segítséget a diákoknak.

Azon hallgatóknak, akik nem írták meg elégséges szinten a tesztet, kötelező volt részt venniük egy felzárkóztató kurzuson. Ennek keretében már a pótolandó hiányosságokra fókuszálhatunk, így segítve az érintetteket az egyetemi matematikatárgyak abszolválásában és a ráépülő szakmai ismeretek sikeres elsajátításában. A kurzuson való részvétel, illetve az elektronikus tananyagok feldolgozása után már jelentősen emelkedett azon diákok száma, akik pótlólagosan, de meg tudták írni a kompetenciatesztet elégséges szinten. Összefoglalva megállapítható, hogy a hallgatók sikeres előrehaladásának támogatásához fontos a bejövő diákok matematikai szintfelmérése. Az eredménytől függően előírt fejlesztő kurzus biztosítása segíthet abban, hogy a hallgatók megfelelő alapokkal indulhassanak a tanulmányaikban.

Irodalomjegyzék

: [1] Homolya Szilvia, Rozgonyi Erika: The results of the university competence measurement in mathematics in the view of the tasks, Mathematics In Education, Research And Applications 8:1 pp. 24–32., 9 p. (2022), https://doi.org/10.15414/meraa.2022.08.01.24-32

[2] Árvai-Homolya Szilvia, Lengyelné Szilágyi Szilvia: Matematika emelt szintű érettségi vizsgák elemzése az informatikai és műszaki alapképzési szakokon elvárt matematikai tudásanyag szempontjából, (In: Talata István (szerk.) Matematikát, Fizikát és Informatikát Oktatók 41. Országos Konferenciája: MAFIOK 2017. Budapest, Szent István Egyetem Ybl Miklós Építéstudományi Kar, p. 79–87. ISBN: 978-963-269-663-8)

[3] Csapodi Csaba: A matematika érettségi követelményeinek változása 2024-től – III. rész, Érintő–Elektronikus matematikai lapok, 29. szám, 2023. szeptember

[4] Csapodi Csaba: A matematika érettségi követelményeinek változása 2024-től – IV. rész, Érintő–Elektronikus matematikai lapok, 30. szám, 2023. december

[5] Homolya Szilvia, Rozgonyi Erika: A 2020-as NAT szerint módosult matematika érettségi követelmények várható hatása az egyetemi oktatásra, Proceedings of the Conference on Problem-based Learning in Engineering Education, Debreceni Egyetem Műszaki Kar, Műszaki Alaptárgyi Tanszék (2023) p. 4–9.

Homolya Szilvia, Rozgonyi Erika
Miskolci Egyetem, Gépészmérnöki és Informatikai Kar, Matematikai Intézet