Információk

Főmenü

 Aktuális szám: 32. szám 2024. június 

Tehetséggondozás a szegedi Radnótiban

Tehetséggondozás a szegedi Radnótiban

 

Tehetséggondozó munka matematikából a Szegedi Radnóti Miklós Kísérleti Gimnáziumban

Iskolánk 1898-ban épült, három neve volt eddigi története során: Magyar Királyi Főgimnázium, Klauzál Gábor Gimnázium, végül 1945 óta Radnóti Miklós Gimnázium. Ennek névváltozataként alakult ki az iskola mostani neve, ami tükrözi a benne folyó sajátos tehetséggondozó munkát. Intézményünk évtizedek óta a felsőoktatási tanulmányokra készíti fel diákjait, az SZTE, ELTE és BME egyik bázisiskolája.

Az iskola tanulói létszáma kb. 800 fő. Az osztályok száma 27, amelyek közül 4-évfolyamos gimnáziumi osztály 16 db (kémia tagozat, biológia tagozat, matematika-fizika tagozat, emelt angol és spanyol óraszámú képzés, humán tagozat), 5-évfolyamos gimnáziumi osztály 5 db (Arany János program) és 6-évfolyamos gimnáziumi osztály 6 db (speciális matematika tagozat, vagyis az M osztály).

A 4-évfolyamos matematika-fizika tagozatos képzés

A Szegedi Radnóti Miklós Kísérleti Gimnáziumban 4-évfolyamos képzési rendben egy-egy fél osztály számára működik a matematika-fizika tagozat, amely mintegy 15 évvel ezelőtt indult ebben a formában. Heti matematikaóráik száma 5-5-6-6 a négy év során. A tananyag a témaköröket tekintve nem haladja meg az emelt szintű érettségi tartalmi követelményeit, viszont a relatíve magasabb heti óraszámnak köszönhetően az egyes témakörökön belül sokkal mélyebbre tudunk jutni. Lehetőség van számos versenyfeladat megoldására is a különböző elméleti részekhez kapcsolódóan, ezzel segítve a felkészülést az Arany Dániel Matematikai Tanulóversenyre és az OKTV-re.

A csoportokat nagyon magas felvételi pontszámmal érkező fiatalokkal tudjuk megtölteni minden évben, akiknek természettudományos, matematika iránti érdeklődéséhez elhivatottság is társul. Ezt bizonyítja, hogy a tanulók minden évben nagy létszámban vesznek részt a különböző matematikaversenyeken és a KöMaL pontversenyeiben. Például ebben a tanévben a 11. évfolyamos csoport 8 tagja szerepel a C-pontverseny első 30 helyezettje között. A csoportokon belüli differenciálás eszköze az úgynevezett évfolyamszakkör a 9., 10. és 11. évfolyamos tanulóknak. Itt hetente 60 percben a legérdeklődőbb „mat-fizes” diákok más, akár „specmatos” évfolyamtársaikkal együtt oldanak meg versenyfeladatokat. Erre az évfolyamszakkörre tehát az adott évfolyam bármely osztálytípusában tanuló diák járhat. A szakköri létszám 10–20 fő, a szakköri foglalkozásokat pedig az aktuális évfolyamon abban a tanévben tanító egy-egy

kolléga vezeti. A tanári munkát itt a kortárscsoport húzóereje is segíti. A diákok meghallgatják egymás megoldásait, tanulnak egymástól, egyszerre ismerik el egymás tudását és versengve motiválják egymást. Ez a tehetségsegítő forma igen sikeresnek bizonyult. Az Arany Dániel Matematikai Tanulóversenyen több diákunk is a díjazottak között szerepelt az elmúlt 10 évben. A matematika OKTV II. kategóriájában is több alkalommal végzett az első 10 versenyző között matematika-fizika tagozatra járó diák. A tapasztalatok alapján úgy gondoljuk, hogy ez az iskolai matematika évfolyamszakkör más intézményekben is könnyen meghonosítható, és remek lehetőséget ad a matematikai tehetség fejlesztésére. 

9.-es évfolyamszakkör, 7. foglalkozás
 
1. Egy szög csúcsa az $A$ pont, szárai $s_1$ és $s_2$. Felvesszük a szög $s_1$ szárán a $B$, $C$, az $s_2$ szárán a $D$, $E$ pontokat úgy, hogy $AB=BD=DC=CE=EA$. Hány fokos a szög?
 
2. Az $ABC$ háromszögben $AB=3\cdot BC$. Legyen $P$ és $Q$ az $AB$ oldal azon pontja, amelyekre $AP=PQ=QB$. Legyen $F$ az $AC$ oldal felezőpontja. Határozzuk meg a $QFP$ szög nagyságát.
 
3. Az $ABCD$ négyzet belsejében felvesszük a $P$ pontot úgy, hogy az $ABP$ háromszög olyan egyenlőszárú háromszög legyen, amelynek alapon fekvő szögei 15 fokosak. Mekkora a $CPD$ szög?
 
4. Az $ABC$ háromszög $AB$ oldala 26 cm. Az $A$ csúcsból induló súlyvonal 18 cm, a $C$ csúcsból induló súlyvonal pedig 15 cm hosszú. Mekkora a háromszög területe?
 
5. Az $ABC$ szabályos háromszögben $D$ és $E$ rendre az $AC$ és $AB$ oldalak pontjai, $P$ pedig a $BD$ és $CE$ szakaszok metszéspontja. Határozzuk meg a $BPE$ szög nagyságát, ha az $AEPD$ négyszög és a $BCP$ háromszög területe egyenlő.
 
6. Hány hegyesszögű, derékszögű, illetve tompaszögű háromszöget határoznak meg egy szabályos húszszög csúcsai?

A csoportok fő célja, hogy mindenki kimagasló eredményt érjen el az emelt szintű matematika érettségin, majd felvételt nyerjen az általa kiválasztott felsőoktatási intézménybe és ott sikeresen és eredményesen megállja a helyét. Ezt el is szokták érni a diákok, hiszen a négy közösen töltött év alatt a szorosan vett tananyag átadásán túl, a csoportok minden tagjának fejlesztjük a képességét az önálló problémamegoldásra, a kitartó, önálló, mély munkára. Így, reményeink szerint, akár a tudományos életben, akár a magánszektorban helyezkednek majd el az egyetemi éveik után, értékes és elismert szakemberek lesznek.

A hatosztályos speciális matematika tagozat

Tagozatunk az egyik legfiatalabb speciális matematika tagozat hazánkban. A radnótis matematikaiskola első osztálya az 1987/88-as tanévben indult, öt évfolyamos képzési formában, gimnáziumunk legendás igazgatója, dr. Bánfalvi József kezdeményezésére. A programban részt vevő matematika szakos kollégák úgy látták, hogy nagymértékben növelné a hatékonyságot, ha már hetedik osztálytól kezdve lehetőség nyílna a mélyebb matematikai ismeretek megalapozására. Ezért az 1988/89-es tanévben megkezdte munkáját – időben az országos szinten is első – hatévfolyamos speciális matematika tagozatos osztály.

Számos vitát váltott ki szakmai körökben a 6-évfolyamos képzés, mivel többen úgy vélték-vélik, hogy egy 6. osztályos gyermek nem maga dönt a továbbtanulásáról, hanem elsősorban a szüleire hallgat. Ebben van igazság, ugyanakkor a kiemelkedő matematikai tehetség már 12 éves korban is jól megfigyelhető, emellett a tehetséges gyerekek nagyszerűen tudnak együtt dolgozni. Nem kell szégyellniük az osztályban, hogy átlagostól eltérő az érdeklődésük, nincsenek olyan korlátaik, amelyek sajnos a legtöbb általános iskolai osztályban fékezik előrehaladásukat.

Bár a korábbi iskolájukhoz képest sok gyereknek erős váltás a matematika tagozat, mégis az a tapasztalat, hogy ha 7. osztály elején a hangsúlyt nem a tárgyi tudásra, hanem a gondolkodás finomítására, élesítésére helyezzük, akkor a többi tudáselem idővel magától beérik. Természetesen a tanár kollégáktól sokkal több energiát igényel egy ilyen típusú osztályban végzett munka. Ez szinte egy külön szakma. Ennek elsajátításában is rengeteget segít egy jelentős szellemi műhely, az ország speciális matematika tagozatain tanító kollégák évenkénti kétnapos találkozója. Ennek fontos részét képezi a bemutató órák megbeszélése, kiváló felkészültségű kollégák tanítási módszereinek megismerése és a szakmai megbeszélések, amelyek mind beépülnek a tanári munkánkba. Nagyon hatékonynak bizonyultak az esti kötetlen baráti beszélgetések is. Évtizedes remek munkakapcsolatok alakultak ki. A más iskolákban folyó jó gyakorlatok átvétele és adaptálása a saját intézményünkben folyó munkához volt talán legfontosabb dolog, ami a radnótis matematika tagozat munkáját segítette. Például az 5. osztályos tehetséggondozó szakkörök ötletét a miskolci Földes Ferenc Gimnáziumból, a hetedikesek heti szorgalmi feladatsorainak beépítését a tananyag feldolgozásába a budapesti Fazekas Gimnáziumból vettük át. Ugyancsak innen kaptuk az inspirációt a matematikából legkiválóbb diákjainknak tartott, évfolyami megkötés nélküli szakkör elindításához és működtetéséhez.

Iskolánk matematikatanárai a speciális matematika tagozat előkészítéseként 5. és 6. osztályos diákoknak általános iskolai szakköröket vezetnek. Az ötödikes foglalkozásokra kb. 45–50, míg a hatodikos szakkörökre kb. 75–80 tanuló jár. A matematika tagozat indulása óta rendezünk a hatodikos tanulóknak külön tehetségkutató versenyt is, ahol 90 perces időkeretben 6 gondolkodtató problémával foglalkozhatnak.

A 7. és 8. osztályban hetente kiadott szorgalmi feladatsorok, melyek megoldásait a következő héten részletesen megbeszéljük, lehetőséget adnak az írásbeli munka csiszolására. A fiatalok megérzik az ízét a felfedezés örömének, ami a magas szintű szellemi munka elengedhetetlen feltétele a későbbiekben. Ugyanakkor azt is megtanulják, hogy milyen formát öltsön a beadott feladatmegoldás, külalak és szerkesztettség szempontjából.

Több sikertelen próbálkozás után arra jöttünk rá, hogy a csoportbontás nem szerencsés 7–8. évfolyamban. Azok az osztályaink bizonyultak a legsikeresebbnek tanulmányi munka és közösség terén is, amelyekben az induló 28–32 diák együtt tevékenykedik a matematikaórán az általános iskolai két év során. A diákok rengeteget tanulnak egymástól, valamint toleránsabbak és megértőbbek lesznek a többiekkel.

Tehetségkutató verseny 6. osztályosoknak, 2023.
 
A megoldásra fordítható idő 90 perc. A megoldások indoklását részletesen le kell írni, az eredmények puszta közlése nem elegendő! A megoldások elkészítéséhez számológép, telefon nem használható. Felhasználható eszközök: toll, ceruza, radír, vonalzó, körző, szögmérő. Egy-egy feladat teljes megoldása 10 pontot ér.
 
1. Anna a spórolt pénzének felét társasjátékokra, a kétötöd részét pedig könyvekre költötte el. Névnapja alkalmából a megmaradt pénzéhez még kapott 4000 Ft-ot az apukájától. Ez alkalomból meghívta a barátnőjét cukrászdába. Itt elköltötte a meglévő összes pénzének kétkilenced részét, ami után 5600 Ft maradt nála.
a) Mennyi volt Anna spórolt pénze?
b) Mennyi pénzt költött Anna könyvekre?
 
2. Egy iskolai rendezvényen 22 diák vett részt. A végén megkérdeztük őket, hogy hány osztálytársuk volt a rendezvényen. Négyen azt válaszolták, hogy 4, hatan azt, hogy 3, és heten azt, hogy 2. Mi lehetett a hiányzó öt válasz?
 
3. A 2023 olyan négyjegyű szám, amelynek 3 db páros és 1 db páratlan számjegye van.
a) Melyik a legnagyobb ilyen tulajdonságú négyjegyű szám?
b) Hány darab 4000-nél kisebb ilyen szám van?
 
4. Az 1, 2, 3, 4, 5, ... egész számok közé felváltva – és $+$ jeleket tettünk. (A 2 előtt – jel van.) Az így kapott műveletsort balról jobbra haladva kezdtük elvégezni. Melyik számig végeztük el a műveleteket, ha az eredmény 2023 lett?
 
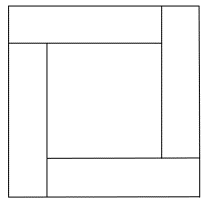
5. Az ábrán egy négyzet köré négy egybevágó téglalapot helyeztünk el. Egy ilyen téglalap kerülete 18 cm, a négyzet területe 25 cm2. Mekkora egy téglalap területe? (Az ábra nem a pontos méreteket tartalmazza.)
 
6. Van 5 db szabályos háromszög alakú egybevágó papírdarabunk. Ezeknek a szabályos háromszöglapoknak az oldalai 2 cm hosszúak. Mind az 5 háromszöget felhasználva összeállítottunk egy sokszöget úgy, hogy a szomszédos háromszögek teljes oldalukkal érintkeznek. Egy lehetséges sokszögtípus látható is az ábrán.
a) Rajzold le, hogy milyen különböző sokszögeket kaphatunk!
b) Mekkora egy-egy ilyen sokszög kerülete?
c) Mekkorák lesznek egy ilyen összerakás után kapott sokszög belső szögei az egyes esetekben?

A 8. osztály végén egy szintfelmérő dolgozat, valamint a két általános iskolai évben végzett munka alapján az M osztályt matematikából két csoportra bontjuk. Jelenleg az egyik csoport a 9–12. osztályban heti 6 órában tanulja a matematikát emelt szinten, de nem speciális matematika tanterv szerint. A másik csoport heti 7-7-8-8 órában, a speciális tanterv szerint halad tovább. A gimnáziumi évek alatt már két matematikatanár tanít az osztályban. A tagozaton folyó komplex tehetségnevelő, tehetségsegítő munkának számos összetevője van. Az osztályban oktató matematikatanárok egymás munkáját ismerve és segítve foglalkoznak a diákokkal. A kollégák szakmai tudása, felkészültsége messze meghaladja az átlagos tanári szintet. Tehetséges diákokkal csak az tud sikeresen foglalkozni, aki állandóan képezi magát és karbantartja tudását. Ez történhet a szakirodalom, illetve a hazai és nemzetközi versenyek feladatanyagának tanulmányozásával, valamint önálló rendszeres feladatmegoldással. A speciális matematika tagozat óráinak az átlagostól eltérő a szerkezete. A felfedeztető matematikaoktatást tartjuk a leghatékonyabb és legmotiválóbb módszernek. Ennek nagyon fontos része, hogy a tanár együtt gondolkodjon a diákokkal, és kérdéseivel segítse, vezesse a tananyag feldolgozását. Ez a tagozat indulása óta így van. Az új, tagozatos tanári munkába belépő kollégák hamar megszeretik és elsajátítják ezt – a tanártól állandó koncentrációt és biztos szakmai tudást igénylő – munkastílust.

Szorgalmi feladatok 7M, 2024. 04. 11.
1. Egy hatszögbe kör írható. A hatszög oldalait felváltva pirosra és kékre színezzük. Bizonyítsuk be, hogy a piros oldalak hosszának összege egyenlő a kék oldalak hosszának összegével.
 
2. Egy 6 m2-es helyiségben kiterítünk három szőnyeget, melyek területe egyenként 3 m2. Bizonyítsuk be, hogy van közöttük kettő, amelyek legalább 1 m2-en átfedik egymást.
 
3. Lefedhető-e a sík véges sok sávval? (A sáv azon pontok halmaza, amely két adott párhuzamos egyenes közötti pontokból áll, a két határoló egyenes pontjait is beleértve.)
 
4. Igazoljuk, hogy egy $n\times n$-es négyzetrács kiparkettázható $5\times 5$-ös, illetve $1\times 3$-as parketták segítségével, ha $n=2021$.
 
5. Egy téglalap egy csúcsból induló oldalai 8 cm és 9 cm. A téglalapot az ábrán látható módon két párhuzamos szakasszal három egyenlő területű részre bontottuk fel. Határozzuk meg a két szakasz távolságát.

Kilencedik osztálytól indul az ún. „szuperszakkör”, amelynek munkájába évfolyam megkötés nélkül iskolánk bármelyik tanulója bekapcsolódhat. Ezeken a 90 perces foglalkozásokon komplex tehetséggondozó munka folyik. Sokszor a matematika különböző területeiről dolgozunk fel egy-egy témát. Máskor meghívott előadók, pl. volt tanítványok, egyetemi oktatók, matematikusok mesélnek a saját kutatási területükhöz kapcsolódó, ugyanakkor középiskolai szinten tárgyalható eredményekről. Itt zajlik a legrangosabb versenyekre való speciális felkészítés is. Ezeken a szakkörökön nagyon sokat tanulnak egymástól a diákok. A kisebbeknek óriási erőt ad az, hogy látják, a nagyobbak milyen mély és szerteágazó ismeretanyaggal rendelkeznek, és persze megértik: erre a tudásra ők is szert tehetnek, ha elég alázat és munkabírás van bennük. Amióta ez a szakköri forma működik megnőtt a matematika versenyeken kimagasló eredményeket elérő diákjaink száma, ami igazolja a kissé szokatlannak számító munkamódszert.

9–12.osztályosok „szuperszakköre”
Egész együtthatós polinomok szorzattá bontása
 
1. Az $a_1$, $a_2$, $\dots$, $a_n$ páronként különböző egész számok, ahol $n\ge 2$ egész szám. Bizonyítsuk be, hogy az $\displaystyle f(x)=(x-a_1)(x-a_2)\dots (x-a_n)-1 $ polinom nem bontható fel legalább elsőfokú, egész együtthatós polinomok szorzatára.
 
2. Az $a_1$, $a_2$, $\dots$, $a_n$ páronként különböző egész számok, ahol $n\ge 2$ egész szám. Bizonyítsuk be, hogy az $\displaystyle f(x)={(x-a_1)}^2{(x-a_2)}^2\dots {(x-a_n)}^2+1 $ polinom nem bontható fel legalább elsőfokú, egész együtthatós polinomok szorzatára.
 
3. Tudjuk, hogy $n\ge 4$, egész szám. Igazoljuk, hogy az $\displaystyle f(x)=x^n+x^3+x^2+x+5 $ polinom nem bontható fel legalább elsőfokú, egész együtthatós polinomok szorzatára.
 
4. Tudjuk, hogy $n\ge 2$, egész szám. Bizonyítsuk be, hogy az $\displaystyle f(x)=x^n+5x^{n-1}+3 $ polinom nem bontható fel legalább elsőfokú, egész együtthatós polinomok szorzatára.
 
5. Legyen $p(x)=a_7x^7+a_6x^6+\dots +a_1x+a_0$ egész együtthatós polinom $(a_7\neq 0)$. Tudjuk, hogy hét különböző egész helyen $\vert p(x)\vert=1$. Bizonyítsuk be, hogy a $p(x)$ polinom nem bontható fel legalább elsőfokú, egész együtthatós polinomok szorzatára.
 
6. Az $a$ 5-tel nem osztható egész szám. Bizonyítsuk be, hogy az $\displaystyle f(x)=x^5-x+a $ polinom nem bontható fel legalább elsőfokú, egész együtthatós polinomok szorzatára.

Tehetségsegítő munkánk fontos eleme, hogy tanulóinkat ösztönözzük a részvételre a Középiskolai Matematikai és Fizikai Lapok feladatmegoldó pontversenyeiben. Ez is hozzájárul ahhoz, hogy tudásukat minden témakörből frissen tartsák, sőt fejlesszék, ne elégedjenek meg az aktuális órai témakör adta problémák megoldásával. A legkiválóbbaknak iskolánk oktatási alapítványa biztosítja, hogy eljárjanak a fővárosi olimpiai szakköre, valamint matematika táborokba, ahol további ismeretekre tehetnek szert, és felmérhetik, hogy hol állnak korosztályuk más diákjaihoz képest. A gimnáziumunkban minden tanévben a matematika tagozatos osztályaink tanulmányi, illetve érettségi átlaga a legkiemelkedőbb. A legmagasabb emelt szintű érettségi átlag mellett, iskolánk történetének három legjobb, 4,98-as, 4,96-os és 4,95-ös, teljes osztályra vonatkozó érettségi átlagát is M-es osztályok érték el. A 2022/2023-as tanévben az M osztály speciális matematika tanterv szerint tanuló felében pl. 97%-os volt a matematika emelt szintű érettségi dolgozatok átlageredménye.

A tagozaton végzett diákok túlnyomó többsége kiválóan megállja a helyét a hazai, sőt a külföldi felsőoktatásban is. Közülük számos kutató, egyetemi oktató került már ki. Húsznál több diákunk végzett, illetve tanul jelenleg is a világ legjobbjai közé tartozó University of Oxford, University of Cambridge és a bostoni MIT egyetemeken.

A speciális matematika tagozaton végzett tehetséggondozó munkánk eredményességét jól mutatja a hazai matematikaversenyeken elért számos kiváló eredmény mellett az is, hogy 2000 óta a nemzetközi matematikaversenyeken (EGMO, MEMO, RMM, IMO) diákjaink kb. 50 alkalommal szerepeltek a magyar csapat tagjai között. A matematika mellett más tantárgyakból is kiválóan teljesítenek az M osztályos diákok. Volt több diákolimpikonunk fizika, kémia és informatika tárgyakból, valamint nyertek OKTV-t diákjaink magyar irodalomból, biológiából, fizikából és orosz nyelvből is.

Természetesen az M osztály nem „versenyistálló”, inkább egy olyan, a tanulókat munkára inspiráló közeg, ahol mindenki kibontakoztathatja képességeit. A nagyon jó közösség kialakulásának alapja a teljesítmény, a tolerancia és a nyitottság. Ezek azok a tulajdonságok, amelyek szinte minden speciális matematika tagozatos osztályunkra jellemzőek. Az M osztály tehát nemcsak a matematikáról szól. Számos diákunknak a matematika ugródeszkaként szolgál ahhoz, hogy más területeken elmélyedve hasznosítsa a tagozaton elsajátított strukturált gondolkodást. Minden osztályban jól érzik magukat azok is, akik nem matematikát választanak továbbtanulási iránynak. Vannak köztük leendő orvosok, jogászok, biológusok, akik akkor sem váltanak osztályt, amikor világossá válik számukra, hogy nem a matematika az elsődleges érdeklődési területük. Tudják, hogy az csak hozzáad egy osztályhoz, azon belül minden emberhez, ha sokszínű a társaság. Jól megfér egymás mellett a leendő mérnök, kutató, pénzügyi szakember, régész, színész, fizikus és még sorolhatnánk, hogy milyen színes is szokott lenni egy M-es osztályközösség. Az a szellemi és általános műveltségbeli koncentráció, ami jó néhány specmat tagozatos osztályunkra jellemző volt és jelenleg is jellemző, iskolánk legnagyobb értékei közé tartozik. Nem lehet véletlen, hogy a tagozat történetében versenyeken és az érettségi vizsgákon is legeredményesebb M osztályok éppen ezek közül a nagyon sokszínű, szerteágazó érdeklődésű diákokból álló osztályokból kerültek ki.

A matematika tagozatos osztályokra jellemző, hogy valóban erős, összetartó osztályközösség ott alakul ki, ahol az első két, még általános iskolai évben sokat dolgoznak a diákok. De úgy, hogy nem rivalizálnak, hanem örülnek annak, ha tanulhatnak egymástól. Ez a mentalitás annak az önzetlenségnek az alapja, amire aztán egy valódi osztályközösség épülhet. Fontos megemlíteni, mekkora szerepe van az osztályfőnöknek abban, hogy milyen lesz egy specmat-tagozatos osztály. Mivel az ilyen osztályokban sok az átlagostól valamilyen szempontból eltérő (ez lehet viselkedés, tehetség, műveltség) diák, így kezdetben nem könnyű elérni, hogy a gyerekek figyeljenek egyrészt egymásra, másrészt a halkabb, visszafogottabb társaikra. A matematika tagozat rendkívül sokat köszönhet azoknak a nem matematika szakos M-es osztályfőnököknek, akik nagy pedagógiai érzékkel, a magas óraszámban tanító matematikatanárokkal együttműködve, egymás munkáját kölcsönösen segítve vezették osztályaikat. Nélkülük a speciális matematika tagozatunk kevésbé lett volna eredményes.

Talán sikerült érzékeltetni, hogy mennyi minden játszik fontos szerepet abban, hogy egy tagozat eredményesen működjön. Jól kitalált képzési forma, kiváló felkészültségű szaktanárok, gondolkodni szerető és egymást tisztelő fiatalok, színes és érdeklődő tanulókból álló osztályközösség, a tagozatos munkát tisztelő és segítő osztályfőnök. Bízunk benne, hogy iskolánk e képzési formája még hosszú évekig biztosítja majd a Szegeden és vonzáskörzetében élő fiataloknak, hogy elmélyülten és eredményesen foglalkozhassanak matematikával.

Ábrahám Gábor, Szaszkó-Bogárné Eckert Bernadett, Schultz János
Szegedi Radnóti Miklós Kísérleti Gimnázium