A Schweitzer Miklós Matematikai Emlékverseny hosszú hagyományokra tekint vissza: 1949 óta minden évben megrendezik. A verseny egyetemisták, különösképpen matematikát tanulók számára szól, és két dolog teszi rendkívül hírhedtté és különlegessé: a formátuma és a nehézsége. A lebonyolítás a következőképpen néz ki: a versenyzők számára 10-12 feladatot tűznek ki, ezek megoldására 10 nap áll rendelkezésre. Bármilyen könyv és segédanyag felhasználható, egyedül külső személy segítségének igénybevétele nem megengedett. Ezeknek a feladatoknak sokszor még az értelmezése is komoly kutatást és utánaolvasást igényel, még matematikát tanuló egyetemisták is sok idegen szót fedezhetnek fel benne. A megoldás ennek megfelelően még ennél is nehezebb, gyakorlatilag egy kutatómunkának megfelelő energiát kell befektetni egy feladatsor megoldásába, és plusz nehézséget okoz az is, hogy nagyon széles körű a feladatok merítése: minden évben az algebra, számelmélet, geometria és analízis legváltozatosabb alterületeiből kerülnek ki a megoldandó problémák.
Néha azonban előfordul, hogy kitűznek egy-egy feladatot, ami akár középiskolások számára is érthető, mind a feladat leírása, mind a megoldása is. Természetesen ez nem azt jelenti, hogy ezek a feladatok egyszerűek lennének, hiszen nem véletlenül válogatták be őket a feladatsorba: megoldásuk változatos ötleteket, sok kreativitást és rengeteg munkát igényel. Mindazonáltal hasznos néha ilyen példákat is mutatni a diákoknak, azt szemléltetve, hogy bár egyáltalán nem könnyű, de még a világ egyik legnehezebb matematikaversenyének is lehetséges megoldani a feladatait. Sokszor érdemes napokig agyalni, próbálkozni egy feladattal, nem feltétlenül csak a legtöbb versenyen megszokott pár órát, mert az igazán nehéz feladatok megfejtése sokszor még több időt vesz igénybe, akár napokig, hetekig is eltarthat. A szerző saját tapasztalatából kiindulva, annak, hogy valaki elinduljon a Schweitzer versenyen, megfelelő táptalaja lehet, ha már középiskolás korában rendszeresen megoldja, beküldi a Középiskolai Matematikai és Fizikai Lapok matematika pontversenyeinek feladatait, gondolva itt főleg a B-jelű pontversenyre, és különösen tehetséges diákok esetén az A-jelűre is.
A következő feladat a 2018-as versenyről való. Bár maga a feladat elsőre geometriai megfogalmazású, de már az elejétől érezhetően gráfelméleti jellegű, ugyanakkor a megoldáshoz nem elég csak ezekre a területekre korlátozódni. A megoldáshoz szükség van számelméleti eszközökre, algebrai számításokra, kombinatorikus gondolatokra, és természetesen rengeteg gráfelméleti és geometriai megfontolásra. Érdekes megfigyelni, hogy több állításon és lemmán keresztül a bizonyítás a középiskolás versenyfeladat-megoldási eszközök széles tárházát vonultatja fel: teljes indukciós és indirekt bizonyítások, moduláris számolások, „vegyük a minimálisat”, és még a determináns is alkalmazásra kerül. Igazi demonstrációja annak, hogy minden, amit felépítünk az évek alatt, végeredményben kapcsolatban áll egymással, és hogy ezekkel az erős eszközökkel nagyon szép és nehéz tételek bizonyítására nyílik lehetőség.
Feladat (Schweitzer, 2018/4.) Legyen 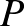 egy véges ponthalmaz a síkon, melyre teljesül, hogy bármely két pontjának távolsága egész szám. Lássuk be, hogy
egy véges ponthalmaz a síkon, melyre teljesül, hogy bármely két pontjának távolsága egész szám. Lássuk be, hogy 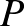 pontjai színezhetőek három színnel úgy, hogy bármely két azonos színű pont távolsága páros legyen.
pontjai színezhetőek három színnel úgy, hogy bármely két azonos színű pont távolsága páros legyen.
Megoldás. Először is, vegyük a problémának egy gráfelméleti átfogalmazását: tekintsük azt a 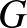 gráfot, aminek a csúcshalmaza
gráfot, aminek a csúcshalmaza 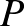 , és két csúcsát pontosan akkor kötjük össze éllel, ha a két pont távolsága páratlan. Ekkor a feladat állítása ekvivalens azzal, hogy
, és két csúcsát pontosan akkor kötjük össze éllel, ha a két pont távolsága páratlan. Ekkor a feladat állítása ekvivalens azzal, hogy 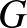 csúcsai színezhetőek 3 színnel úgy, hogy azonos színú pontok között nem fut él, azaz
csúcsai színezhetőek 3 színnel úgy, hogy azonos színú pontok között nem fut él, azaz 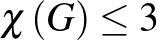 , ahol
, ahol 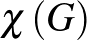 a
a 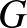 gráf kromatikus számát jelöli.
gráf kromatikus számát jelöli.
1. Definíció. A 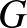 egyszerű gráf
egyszerű gráf 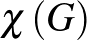 -vel jelölt kromatikus száma az a legkisebb színszám, ahány szín felhasználásával
-vel jelölt kromatikus száma az a legkisebb színszám, ahány szín felhasználásával 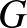 összes csúcsa kiszínezhető úgy, hogy
összes csúcsa kiszínezhető úgy, hogy 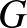 minden élének két végpontja különböző színű legyen.
minden élének két végpontja különböző színű legyen.
Ebben a megfogalmazásban gondolkozzunk el, miről is szól igazából ez a feladat: tekintünk pontokat a síkon, amik közül bármely kettő távolsága egész, és ennek a felállásnak a geometriája strukturálisan korlátozza a fellépő páratlan távolságokat, amit itt a 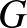 gráf kromatikus száma fejez ki. Ez a kromatikus szám egyelőre még megfoghatatlannak tűnik, de könnyű találni egy gyengébb, viszont annál szemléletesebb feltételt:
gráf kromatikus száma fejez ki. Ez a kromatikus szám egyelőre még megfoghatatlannak tűnik, de könnyű találni egy gyengébb, viszont annál szemléletesebb feltételt:
1. Állítás. Adott a síkon  pont, amelyek közül bármely kettő távolsága egész. Ekkor a pontok között fellépő távolságok közül legalább az egyik páros.
pont, amelyek közül bármely kettő távolsága egész. Ekkor a pontok között fellépő távolságok közül legalább az egyik páros.
Ez egy szükséges (de nem elégséges!) feltétele annak, hogy a feladat állítása igaz legyen, hiszen ha lenne 4 pont, amely közül bármely kettő távolsága páratlan, akkor a 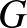 gráf bármely színezésében ennek a 4 pontnak különböző színűnek kellene lennie, vagyis a kromatikus szám legalább 4 lenne.
gráf bármely színezésében ennek a 4 pontnak különböző színűnek kellene lennie, vagyis a kromatikus szám legalább 4 lenne.
Bizonyítás. Tegyük fel indirekt módon, hogy a 4 pont között fellépő mind a 6 távolság páratlan. Jelölje ezeket a pontokat 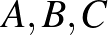 és
és  , a megfelelő távolságokat pedig
, a megfelelő távolságokat pedig 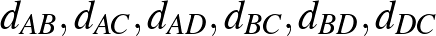 . A kulcsötlet a bizonyításban, hogy számoljuk ki az
. A kulcsötlet a bizonyításban, hogy számoljuk ki az 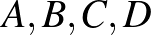 pontok által meghatározott tetraéder térfogatát 3 dimenzióban: ez egyrészt nyilvánvalóan 0, hiszen a 4 pont egy síkban fekszik. Másrészt, ahogyan két dimenzióban háromszögekre a Héron-képlet, ugyanúgy tetraéderekre is létezik egy formula, ami a csúcsok távolságának függvényében megadja a tetraéder térfogatát, ez az úgynevezett Cayley–Menger-determináns, ami azt mondja ki, hogy ha az
pontok által meghatározott tetraéder térfogatát 3 dimenzióban: ez egyrészt nyilvánvalóan 0, hiszen a 4 pont egy síkban fekszik. Másrészt, ahogyan két dimenzióban háromszögekre a Héron-képlet, ugyanúgy tetraéderekre is létezik egy formula, ami a csúcsok távolságának függvényében megadja a tetraéder térfogatát, ez az úgynevezett Cayley–Menger-determináns, ami azt mondja ki, hogy ha az 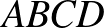 tetraéder térfogata
tetraéder térfogata 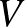 , akkor
, akkor
![$\displaystyle 288V^2= \begin{vmatrix}
0 & 1 & 1 & 1 & 1\\ [3pt]
1 & 0 & d_{AB}^...
...2 & 0 & d_{CD}^2\\ [3pt]
1 & d_{AD}^2 & d_{BD}^2 & d_{CD}^2 & 0
\end{vmatrix}.
$](/images/stories/latexuj/2024-05/2024-05-schweitzerfeladatcikk/img12.png)
Ennek a kifejezésnek a bal oldala 0. Másrészt, feltevésünk szerint mindegyik távolság páratlan, és ismert, hogy páratlan számok négyzete 8-cal osztva mindig 1 maradékot ad. Ezt felhasználva, a jobb oldal értéke modulo 8:
![$\displaystyle \begin{vmatrix}
0 & 1 & 1 & 1 & 1\\ [3pt]
1 & 0 & d_{AB}^2 & d_{A...
... [3pt]
1 & 1 & 1 & 0 & 1\\ [3pt]
1 & 1 & 1 & 1 & 0 \end{vmatrix} = 4 \pmod{8}.
$](/images/stories/latexuj/2024-05/2024-05-schweitzerfeladatcikk/img13.png)
Ez viszont ellentmondás, hiszen modulo 8 a bal oldal 0-val, a jobb oldal 4-gyel egyenlő. Tehát nem lehet minden távolság páratlan. 
Így tehát kizártuk, hogy 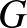 -ben megjelenjen a 4 csúcsú teljes gráf (feszített) részgráfként. Ez még nem elég ahhoz, hogy biztosítsuk, hogy a gráf kromatikus száma legfeljebb 3. Ugyanakkor vegyük észre, hogy az előző bizonyításban maradt még „kakaó”: a determináns, amit felírunk a távolságok alapján, talán más típusú részgráfok esetén sem 0, és ezért további gráfokat is ki tudnánk zárni
-ben megjelenjen a 4 csúcsú teljes gráf (feszített) részgráfként. Ez még nem elég ahhoz, hogy biztosítsuk, hogy a gráf kromatikus száma legfeljebb 3. Ugyanakkor vegyük észre, hogy az előző bizonyításban maradt még „kakaó”: a determináns, amit felírunk a távolságok alapján, talán más típusú részgráfok esetén sem 0, és ezért további gráfokat is ki tudnánk zárni 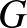 (feszített) részgráfjai közül. Ez valóban így is van, ahogy a következő állításban meg is mutatjuk. Mielőtt azonban még erre rátérnénk, érdemes tisztázni, mi a különbség egy gráf részgráfja és feszített részgráfja között, mert a bizonyítás további részeinek teljes megértéséhez elengedhetetlenül szükséges ezen fogalmak elkülönítése.
(feszített) részgráfjai közül. Ez valóban így is van, ahogy a következő állításban meg is mutatjuk. Mielőtt azonban még erre rátérnénk, érdemes tisztázni, mi a különbség egy gráf részgráfja és feszített részgráfja között, mert a bizonyítás további részeinek teljes megértéséhez elengedhetetlenül szükséges ezen fogalmak elkülönítése.
2. Definíció. Egy gráf feszített részgráfja egy olyan gráf, melynek csúcsai az eredeti gráf csúcsainak egy részhalmaza, élei pedig a részhalmazban szereplő csúcsokat összekötő élek. Másként fogalmazva,  lesz feszített részgráfja
lesz feszített részgráfja 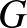 -nek, ha vesszük
-nek, ha vesszük 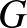 bizonyos csúcsait és minden köztük futó élt.
bizonyos csúcsait és minden köztük futó élt.
Tehát minden alkalommal, amikor feszített részgráfról beszélünk, kiválasztjuk az eredeti 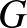 gráf csúcsainak egy részhalmazát, és
gráf csúcsainak egy részhalmazát, és  közöttük futó élt, és
közöttük futó élt, és  csak ezeket az éleket.
csak ezeket az éleket.
2. Állítás. 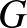 nem tartalmazhat 4 csúcsból álló utat feszített részgráfként, azaz nem lehet olyan
nem tartalmazhat 4 csúcsból álló utat feszített részgráfként, azaz nem lehet olyan 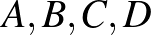 csúcsa, hogy
csúcsa, hogy  ,
, 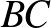 és
és 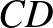 között fut él, de
között fut él, de 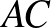 ,
, 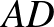 , és
, és 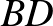 között nem fut él.
között nem fut él.
Bizonyítás. A bizonyítás ugyanúgy megy, mint az előző állítás esetében: indirekt feltéve, hogy létezik 4 csúcsú út feszített részgráfként, a determináns értékének egyrészt 0-nak kell lennie, hiszen a megfelelő tetraéder térfogata 0; másrészt viszont most modulo 4 felírva a determinánst az esetünkben (felhasználva, hogy páratlan számok négyzete 1 modulo 4, és páros számok négyzete 0 modulo 4):
![$\displaystyle \begin{vmatrix}
0 & 1 & 1 & 1 & 1\\ [3pt]
1 & 0 & d_{AB}^2 & d_{A...
...[3pt]
1 & 0 & 1 & 0 & 1\\ [3pt]
1 & 0 & 0 & 1 & 0 \end{vmatrix} = -2 \pmod{4},
$](/images/stories/latexuj/2024-05/2024-05-schweitzerfeladatcikk/img24.png)
ami ellentmondás. 
Az egyszerűség kedvéért jelöljük a továbbiakban a 4 csúcsú teljes gráfot 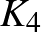 -gyel, a 4 csúcsból álló utat pedig
-gyel, a 4 csúcsból álló utat pedig 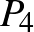 -gyel. Beláttuk tehát, hogy a
-gyel. Beláttuk tehát, hogy a 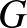 gráf struktúrájában létezik a következő két megkötés: nem tartalmazza se
gráf struktúrájában létezik a következő két megkötés: nem tartalmazza se 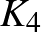 -et, se
-et, se 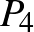 -et feszített részgráfként. Kissé meglepő módon kiderül, hogy ez a két dolog elégséges is: be fogjuk bizonyítani, hogy ha egy gráf nem tartalmazza
-et feszített részgráfként. Kissé meglepő módon kiderül, hogy ez a két dolog elégséges is: be fogjuk bizonyítani, hogy ha egy gráf nem tartalmazza 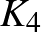 -et és
-et és 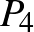 -et feszített részgráfként, akkor kromatikus száma legfeljebb 3.
-et feszített részgráfként, akkor kromatikus száma legfeljebb 3.
Jelölje egy tetszőleges  gráf komplementerét
gráf komplementerét 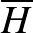 , vagyis azt a gráfot, aminek csúcshalmaza megegyezik
, vagyis azt a gráfot, aminek csúcshalmaza megegyezik  csúcshalmazával, és két csúcs pontosan akkor van benne összekötve, ha
csúcshalmazával, és két csúcs pontosan akkor van benne összekötve, ha  -ban nincs.
-ban nincs.
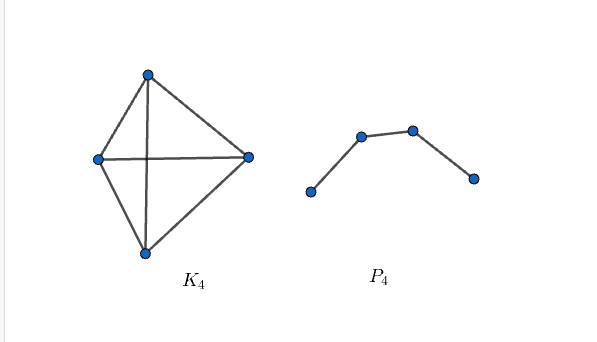
Vegyük észre, hogy a 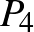 gráf komplementere szintén egy
gráf komplementere szintén egy 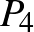 gráf, azaz a négyelemű út egy olyan gráf, amelynek komplementere izomorf önmagával. Speciálisan tehát
gráf, azaz a négyelemű út egy olyan gráf, amelynek komplementere izomorf önmagával. Speciálisan tehát 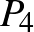 olyan gráf, amire igaz, hogy saját maga és a komplementere is összefüggő. A következő lemmában megmutatjuk, hogy gráfokban ez utóbbi tulajdonságot tudjuk karakterizálni
olyan gráf, amire igaz, hogy saját maga és a komplementere is összefüggő. A következő lemmában megmutatjuk, hogy gráfokban ez utóbbi tulajdonságot tudjuk karakterizálni 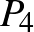 segítségével.
segítségével.
1. Lemma. Legyen a  egyszerű gráf csúcshalmaza
egyszerű gráf csúcshalmaza 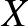 . Ekkor a következő állítások ekvivalensek:
. Ekkor a következő állítások ekvivalensek:
(i)  -ban van
-ban van 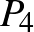 -gyel izomorf feszített részgráf;
-gyel izomorf feszített részgráf;
(ii) 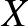 -nek létezik olyan, legalább kételemű részhalmaza, ami
-nek létezik olyan, legalább kételemű részhalmaza, ami  -ban és
-ban és 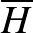 -ben is összefüggő.
-ben is összefüggő.
Bizonyítás. Az (i) 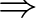 (ii) következtetéshez elég vennünk egy
(ii) következtetéshez elég vennünk egy 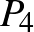 -gyel izomorf feszített részgráfot
-gyel izomorf feszített részgráfot  -ban, amelynek csúcshalmaza a fentiek szerint
-ban, amelynek csúcshalmaza a fentiek szerint 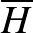 -ben is
-ben is 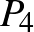 -gyel izomorf részgráfot feszít ki.
-gyel izomorf részgráfot feszít ki.
A másik irányhoz tegyük fel, hogy létezik csúcsoknak egy olyan részhalmaza, ami legalább kételemű és  -ban és
-ban és 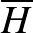 -ben is összefüggő. Legyen
-ben is összefüggő. Legyen  egy minimális elemszámú az ilyen tulajdonságokkal bíró csúcshalmazok között. Vegyük észre, hogy
egy minimális elemszámú az ilyen tulajdonságokkal bíró csúcshalmazok között. Vegyük észre, hogy  legalább négyelemű, hiszen könnyen ellenőrizhetjük, hogy nincs ilyen tulajdonságú 2 vagy 3 csúcsú gráf. Legyen
legalább négyelemű, hiszen könnyen ellenőrizhetjük, hogy nincs ilyen tulajdonságú 2 vagy 3 csúcsú gráf. Legyen  tetszőleges. A minimalitás miatt ekkor
tetszőleges. A minimalitás miatt ekkor 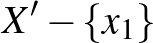 vagy nem összefüggő
vagy nem összefüggő  -ban, vagy nem összefüggő
-ban, vagy nem összefüggő 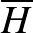 -ben. Mivel
-ben. Mivel  és
és 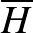 szerepe felcserélhető, így feltehetjük, hogy
szerepe felcserélhető, így feltehetjük, hogy 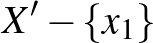 nem összefüggő
nem összefüggő  -ban (vegyük észre, hogy ezt a felcserélést megtehetjük, mert
-ban (vegyük észre, hogy ezt a felcserélést megtehetjük, mert 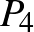 komplementere izomorf önmagával, ezért ha a megcserelés után a bizonyítás talál
komplementere izomorf önmagával, ezért ha a megcserelés után a bizonyítás talál 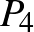 -et
-et 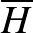 -ben, akkor ez biztosítja azt is, hogy lesz
-ben, akkor ez biztosítja azt is, hogy lesz 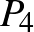
 -ban). Mivel
-ban). Mivel  összefüggő
összefüggő 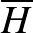 -ben, és legalább kételemű, ezért létezik
-ben, és legalább kételemű, ezért létezik 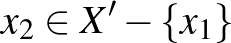 , ami szomszédos
, ami szomszédos 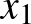 -gyel
-gyel 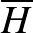 -ben (vagyis
-ben (vagyis  -ban nem fut
-ban nem fut 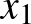 és
és 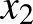 között él). Mivel
között él). Mivel 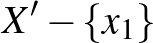 nem összefüggő
nem összefüggő  -ban, így az ez által a csúcshalmaz által indukált részgráfnak
-ban, így az ez által a csúcshalmaz által indukált részgráfnak  -ban legalább két összefüggőségi komponense van. Legyen
-ban legalább két összefüggőségi komponense van. Legyen 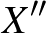 ahhoz az összefüggőségi komponenshez tartozó csúcshalmaz, ami tartalmazza
ahhoz az összefüggőségi komponenshez tartozó csúcshalmaz, ami tartalmazza 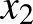 -t.
-t. 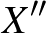 és
és  egyaránt nemüres, és a két halmaz között nem fut
egyaránt nemüres, és a két halmaz között nem fut  -ban él.
-ban él.
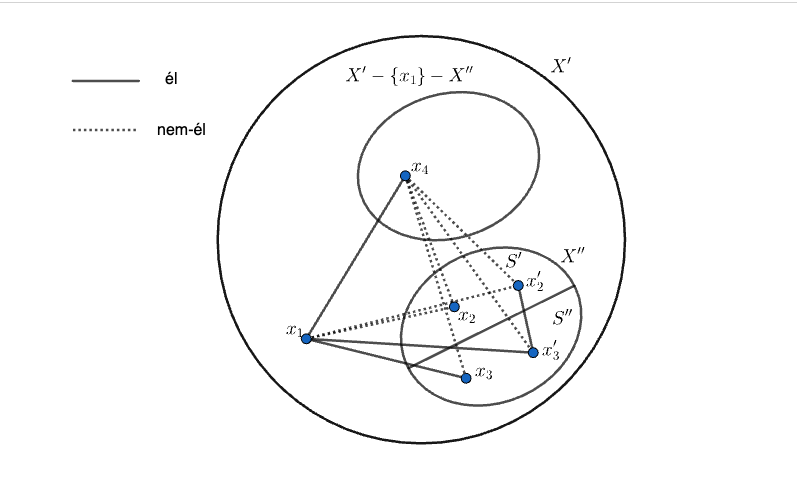
Mivel  összefüggő
összefüggő  -ban, ezért ez csak úgy lehet, ha létezik
-ban, ezért ez csak úgy lehet, ha létezik 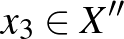 és
és 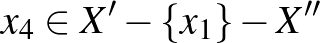 úgy, hogy mind a kettő össze van kötve
úgy, hogy mind a kettő össze van kötve 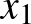 -gyel
-gyel  -ban.
-ban.
Legyen 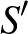 azon elemek halmaza
azon elemek halmaza 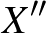 -ben, amik nincsenek összekötve
-ben, amik nincsenek összekötve  -ban (azaz össze vannak kötve
-ban (azaz össze vannak kötve 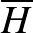 -ben)
-ben) 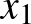 -gyel,
-gyel,  pedig azon
pedig azon 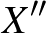 -beli csúcsok halmaza, amik össze vannak kötve
-beli csúcsok halmaza, amik össze vannak kötve  -ban
-ban 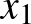 -gyel. Ekkor
-gyel. Ekkor 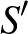 és
és  diszjunkt halmazok és
diszjunkt halmazok és 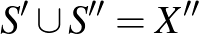 . Mivel
. Mivel 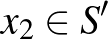 ,
, 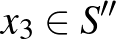 , így mindkét halmaz nemüres, és az uniójuk,
, így mindkét halmaz nemüres, és az uniójuk, 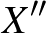 , egy feszített részgráf összefüggőségi komponense
, egy feszített részgráf összefüggőségi komponense  -ban, ezért létezik
-ban, ezért létezik 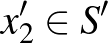 ,
, 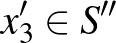 , amik éllel össze vannak kötve
, amik éllel össze vannak kötve  -ban. Így az
-ban. Így az 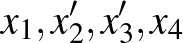 pontok olyanok, hogy
pontok olyanok, hogy 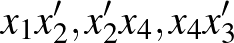 élek
élek 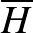 -ben (azaz nem élek
-ben (azaz nem élek  -ban) és
-ban) és 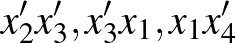 élek
élek  -ban, vagyis az
-ban, vagyis az 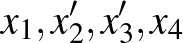 csúcsok által feszített részgráf
csúcsok által feszített részgráf  -ban és
-ban és  -ben is
-ben is  -gyel izomorf.
-gyel izomorf. 
Jelölje tetszőleges  gráf esetén
gráf esetén 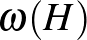 a
a  klikkszámát, vagyis a legtöbb olyan csúcs számát, amit ki tudunk választani úgy, hogy bármely kettő között fusson él.
klikkszámát, vagyis a legtöbb olyan csúcs számát, amit ki tudunk választani úgy, hogy bármely kettő között fusson él.
2. Lemma. Ha egy  gráfban nincs
gráfban nincs 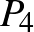 -gyel izomorf feszített részgráf, akkor
-gyel izomorf feszített részgráf, akkor  .
.
Bizonyítás. A csúcsok számára vonatkozó teljes indukcióval bizonyítunk. Egycsúcsú gráfra az állítás nyilvánvalóann igaz. Legyen  tetszőleges, legalább kétcsúcsú gráf, amiben nincs
tetszőleges, legalább kétcsúcsú gráf, amiben nincs 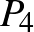 -gyel izomorf feszített részgráf, és tegyük fel, hogy az állítás igaz minden
-gyel izomorf feszített részgráf, és tegyük fel, hogy az állítás igaz minden  -nál kisebb csúcsszámú gráfra. Az előző lemmából következik, hogy ekkor
-nál kisebb csúcsszámú gráfra. Az előző lemmából következik, hogy ekkor  -nak tetszőleges
-nak tetszőleges 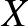 csúcshalmazára
csúcshalmazára 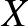 vagy nem összefüggő
vagy nem összefüggő  -ban, vagy nem összefüggő
-ban, vagy nem összefüggő 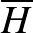 -ben. Ezt
-ben. Ezt 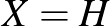 -ra alkalmazva kapjuk, hogy vagy
-ra alkalmazva kapjuk, hogy vagy  , vagy
, vagy 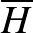 nem összefüggő.
nem összefüggő.
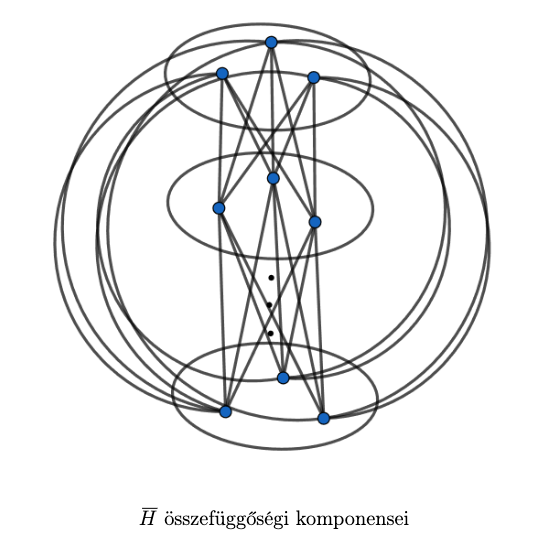
Ha  nem összefüggő, akkor jelöljük
nem összefüggő, akkor jelöljük  -vel
-vel 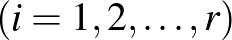 az összefüggőségi komponenseit. Mivel komponensek között nem fut él, ezért
az összefüggőségi komponenseit. Mivel komponensek között nem fut él, ezért 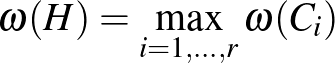 . Szintén amiatt, hogy nem fut a kompnensek között él, ezért külön-külön is tudjuk színezni őket, ezért adódik, hogy
. Szintén amiatt, hogy nem fut a kompnensek között él, ezért külön-külön is tudjuk színezni őket, ezért adódik, hogy 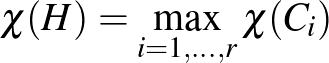 . Az indukciós feltétel miatt
. Az indukciós feltétel miatt  (alkalmazható a feltevés, hiszen mivel a
(alkalmazható a feltevés, hiszen mivel a  -k feszített részgráfok, ezért nem tartalmazhatnak
-k feszített részgráfok, ezért nem tartalmazhatnak 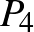 -et feszített részgráfként és
-et feszített részgráfként és  ), így
), így 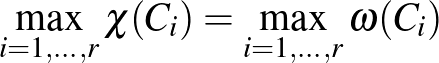 , vagyis
, vagyis  .
.
Ha  nem összefüggő, akkor legyenek
nem összefüggő, akkor legyenek 
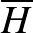 összefüggőségi komponensei. Ekkor
összefüggőségi komponensei. Ekkor 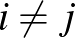 esetén
esetén  minden eleme össze van kötve
minden eleme össze van kötve 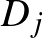 minden elemével
minden elemével  -ban. Tehát színezés esetén minden színt csak egy komponensen belül használhatunk, és klikkeket is úgy kapunk, hogy minden komponensből kiválasztunk egy klikket, és az klikk lesz
-ban. Tehát színezés esetén minden színt csak egy komponensen belül használhatunk, és klikkeket is úgy kapunk, hogy minden komponensből kiválasztunk egy klikket, és az klikk lesz  -ban is. Ezért
-ban is. Ezért 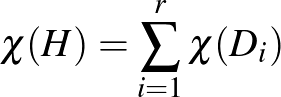 és
és 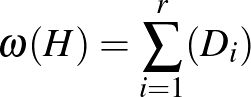 , a
, a  -k feszített részgráfok
-k feszített részgráfok  -ban,
-ban,  , ezért az indukciós feltevést alkalmazva
, ezért az indukciós feltevést alkalmazva 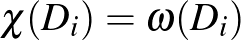 és így
és így  .
. 
Ebből viszont már következik a fentiek alapján a feladat állítása: mivel 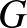 nem tartalmaz
nem tartalmaz 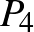 -et feszített részgráfként, ezért
-et feszített részgráfként, ezért 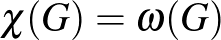 , másrészt mivel
, másrészt mivel 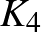 -et sem tartalmaz feszített részgráfként, ezért
-et sem tartalmaz feszített részgráfként, ezért 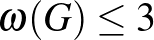 , vagyis
, vagyis 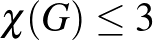 , és éppen ezt akartuk belátni.
, és éppen ezt akartuk belátni.
Szőke Tamás
Szőke Tamás 2015-ben végzett a Földes Ferenc Gimnázium speciális matematika tagozatán, majd az Eötvös Loránd Tudományegyetem matematikus hallgatója volt. Középiskolás évei alatt számos országos eredményt ért el matematikából: 10. helyezés az Országos Középiskolai Tanulmányi Verseny III. kategóriájában, 9–10. helyezés a Középiskolai Matematikai Lapok A pontjelű és 13. a B pontjelű versenyén, dicséret a Romanian Master of Mathematics nemzetközi matematikaversenyen, valamint bronzérem a Közép-európai Matematikai Diákolimpián (MEMO). A versenyzést az egyetemen is folytatta, ahol I. díjat szerzett az egyetemisták nemzetközi matematikaversenyén (International Mathematics Competition for University Students, rövidítve: IMC), illetve 2018-ban 1. helyen végzett a Schweitzer Miklós Matematikai Emlékversenyen. Egyetemi évei alatt több alkalommal részt vett a Földes Ferenc Gimnázium matematikai tehetséggondozó munkájában. Jelenleg Svájcban dolgozik kvantitatív fejlesztő munkakörben. (A szerk.)











