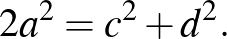Középiskolai tanárként (és persze diákként is) szeretjük az olyan egész együtthatós, 1 főegyütthatójú másodfokú egyenleteket, amelyeknek egész gyökei vannak. A középiskolai tanulmányok során számtalan ilyen egyenlettel találkozunk, és megesik, hogy ezek között valamilyen kapcsolatot is felfedezünk.
 Például az
Például az 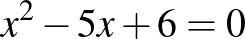 és az
és az 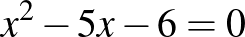 egyenletek gyökei egyaránt egész számok. Másik ilyen „szerencsés” páros a következő két egyenlet:
egyenletek gyökei egyaránt egész számok. Másik ilyen „szerencsés” páros a következő két egyenlet: 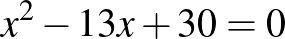 és
és 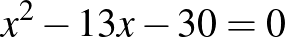 . Mindkét esetben a konstans tag előjelét megváltoztatva olyan másodfokú egyenletet kaptunk, amelynek szintén egész számok a gyökei, csakúgy, mint az eredetinek.
. Mindkét esetben a konstans tag előjelét megváltoztatva olyan másodfokú egyenletet kaptunk, amelynek szintén egész számok a gyökei, csakúgy, mint az eredetinek.
Matematika szakkörön és matematika tagozaton felvethetők az alábbi kérdések:
– Hány ilyen tulajdonságú páros létezik?
– Egyáltalán véges vagy végtelen sok van belőlük?
– Hogyan lehet ilyen egyenletpárokat előállítani a fenti két példán kívül (ha egyáltalán vannak)?
Ezekre a kérdésekre keressük a választ ebben a cikkben, és a probléma megoldásában a komplex számokat is segítségül hívjuk.
Az első dolog, amire érdemes kitérni, hogy ha az elsőfokú tag együtthatójának az előjelét változtatjuk meg, akkor az új gyökök az eredeti gyökök ellentettjei lesznek, vagyis, ha eredetileg egész számok voltak, akkor azok is maradnak. Ez azonnal kiolvasható a megoldóképletből. A konstans tag előjelének megváltoztatása viszont a legtöbb esetben a diszkriminánst is megváltoztatja, így egyáltalán nem nyilvánvaló, hogy egész gyököket kapunk a változtatás után.
A probléma tehát a következő: melyek azok az 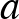 és
és 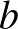 egész számok, amelyekre az
egész számok, amelyekre az 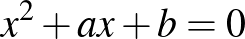 és az
és az 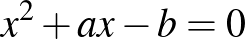 másodfokú egyenletek gyökei egyaránt egész számok?
másodfokú egyenletek gyökei egyaránt egész számok?
Mint az előző megjegyzésből is következik, 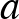 előjele nem befolyásolja a vizsgálatainkat (és természetesen
előjele nem befolyásolja a vizsgálatainkat (és természetesen 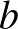 előjele sem). Ha
előjele sem). Ha 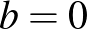 , akkor minden
, akkor minden 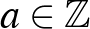 -re olyan egyenleteket kapunk, amelyeknek egész gyökei vannak (0 és
-re olyan egyenleteket kapunk, amelyeknek egész gyökei vannak (0 és 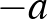 ). Ezek a feladatunk triviális megoldásai, amelyekből nyilván végtelen sok van, de nem túl érdekesek a számunkra. Innentől a nemtriviális megoldásokat vizsgáljuk, vagyis feltesszük, hogy
). Ezek a feladatunk triviális megoldásai, amelyekből nyilván végtelen sok van, de nem túl érdekesek a számunkra. Innentől a nemtriviális megoldásokat vizsgáljuk, vagyis feltesszük, hogy 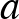 ,
,  . Ahhoz, hogy mindkét másodfokú egyenlet gyökei egészek legyenek, szükséges, hogy mindkét egyenlet diszkriminánsa négyzetszám legyen. Ez viszont elegendő is hozzá, mert a megoldóképletben szereplő számláló (
. Ahhoz, hogy mindkét másodfokú egyenlet gyökei egészek legyenek, szükséges, hogy mindkét egyenlet diszkriminánsa négyzetszám legyen. Ez viszont elegendő is hozzá, mert a megoldóképletben szereplő számláló (  ) két tagjának paritása megegyezik, ezért ha 2-vel osztjuk, egész számokat kapunk.
) két tagjának paritása megegyezik, ezért ha 2-vel osztjuk, egész számokat kapunk.
Az egyenletek diszkriminánsai: 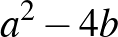 és
és 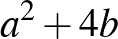 . Ezeknek kell négyzetszámnak lenniük, vagyis valamilyen
. Ezeknek kell négyzetszámnak lenniük, vagyis valamilyen 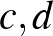 pozitív egész számokra fenn kell állnia a következő összefüggéseknek:
pozitív egész számokra fenn kell állnia a következő összefüggéseknek:
és
Itt  és
és  nem lehet egyenlő egymással, mert akkor
nem lehet egyenlő egymással, mert akkor 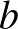 értéke 0 lenne, és visszajutnánk a triviális megoldásokhoz. Ha összeadjuk (1)-et és (2)-t, akkor a következőt kapjuk:
értéke 0 lenne, és visszajutnánk a triviális megoldásokhoz. Ha összeadjuk (1)-et és (2)-t, akkor a következőt kapjuk:
Vagyis a 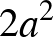 olyan szám, amely előáll két különböző négyzetszám összegeként. Ez a gondolatmenet visszafelé is működik: ha
olyan szám, amely előáll két különböző négyzetszám összegeként. Ez a gondolatmenet visszafelé is működik: ha 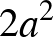 előáll
előáll 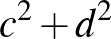 alakban, ahol
alakban, ahol 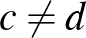 , akkor a (3) átrendezésével kapjuk:
, akkor a (3) átrendezésével kapjuk: 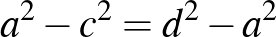 .
.
– Ha 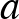 páros, akkor
páros, akkor 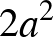 osztható 8-cal, így (3) miatt
osztható 8-cal, így (3) miatt 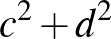 is. Ez viszont csak úgy lehetséges, ha
is. Ez viszont csak úgy lehetséges, ha 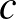 és
és 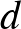 is páros. Ekkor tehát
is páros. Ekkor tehát 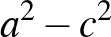 és
és 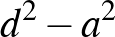 is osztható 4-gyel.
is osztható 4-gyel.
– Ha 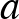 páratlan, akkor
páratlan, akkor 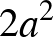 -nek a 4-es maradéka 2, így (3) miatt
-nek a 4-es maradéka 2, így (3) miatt 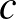 és
és 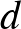 is páratlanok. Ebben az esetben is teljesül tehát, hogy
is páratlanok. Ebben az esetben is teljesül tehát, hogy 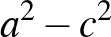 és
és 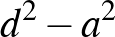 osztható 4-gyel. Vagyis
osztható 4-gyel. Vagyis 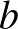 megkapható
megkapható 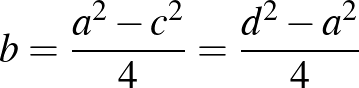 alakban (természetesen
alakban (természetesen 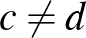 miatt
miatt 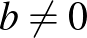 ), és innen visszakapjuk az (1) és (2) összefüggéseket.
), és innen visszakapjuk az (1) és (2) összefüggéseket.
Azt állapítottuk meg tehát, hogy pontosan azokhoz az 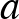 pozitív egész számokhoz létezik olyan
pozitív egész számokhoz létezik olyan 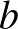 pozitív egész szám, amelyekre az
pozitív egész szám, amelyekre az 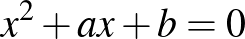 és az
és az 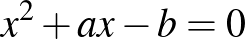 másodfokú egyenletek gyökei egész számok, amely
másodfokú egyenletek gyökei egész számok, amely 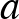 számok esetében
számok esetében  előáll két különböző négyzetszám összegeként. A kérdés az, hogy hogyan lehet egy ilyen előállítást „elkészíteni”.
előáll két különböző négyzetszám összegeként. A kérdés az, hogy hogyan lehet egy ilyen előállítást „elkészíteni”.
Erre fogunk példát látni az alábbiakban. Komplex számok segítségével dolgozunk, és felhasználjuk a komplex számok körében megismert műveleteket és műveleti tulajdonságokat.
1. példa. Legyen 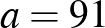 :
:
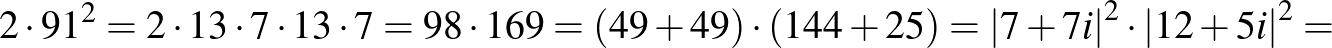
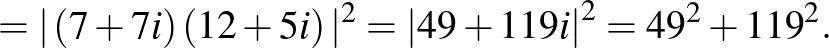
Tehát 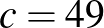 és
és 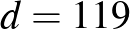 , így
, így 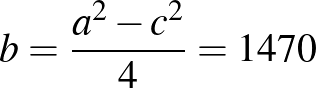 . Így a megfelelő egyenletpár:
. Így a megfelelő egyenletpár: 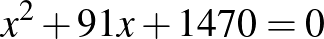 (a gyökei
(a gyökei 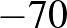 és
és 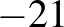 ) és
) és 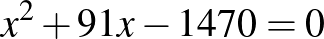 (a gyökök
(a gyökök  és 14). Természetesen 91 helyett
és 14). Természetesen 91 helyett 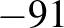 -et is lehet írni
-et is lehet írni 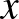 együtthatójaként. Vegyük észre, hogy a számolás során felhasználtuk, hogy a 91 összetett szám, és így több prímtényező szorzatára bontható.
együtthatójaként. Vegyük észre, hogy a számolás során felhasználtuk, hogy a 91 összetett szám, és így több prímtényező szorzatára bontható.
2. példa. Vizsgáljunk meg most egy olyan esetet, amikor 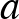 prímszám. Legyen például
prímszám. Legyen például 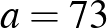 :
:
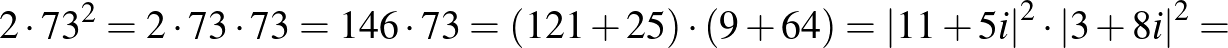
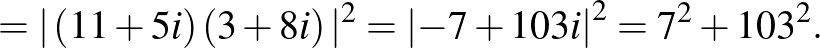
Ebben az esetben  és
és 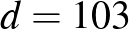 , így
, így 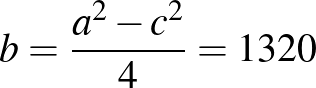 . Tehát a megfelelő egyenletpár:
. Tehát a megfelelő egyenletpár:  (a gyökei
(a gyökei 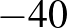 és
és 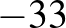 ) és
) és  (a gyökök
(a gyökök  és 15).
és 15).
3. példa. Nézzünk meg olyan esetet is, amikor 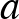 páros szám és nem négyzetmentes! Legyen például
páros szám és nem négyzetmentes! Legyen például  :
:

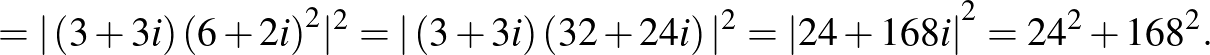
Így tehát 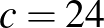 és
és 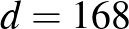 , ezért
, ezért 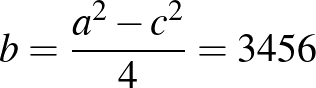 . Vagyis a megfelelő egyenletpár:
. Vagyis a megfelelő egyenletpár: 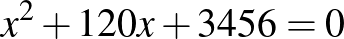 (a gyökei
(a gyökei 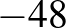 és
és 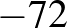 ) és
) és 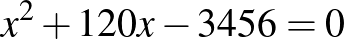 (a gyökök
(a gyökök 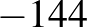 és 24).
és 24).
Ez a három példa jól mutatja, hogyan keressünk a cikk elején bemutatott egyenletpárokhoz hasonlókat: a 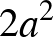 számot bontsuk fel két (vagy több) olyan szám szorzatára, amelyek maguk is előállnak két négyzetszám összegeként, majd pedig használjuk fel a komplex számok szorzására és abszolútértékére vonatkozó szabályokat. Az persze kérdés, hogy milyen
számot bontsuk fel két (vagy több) olyan szám szorzatára, amelyek maguk is előállnak két négyzetszám összegeként, majd pedig használjuk fel a komplex számok szorzására és abszolútértékére vonatkozó szabályokat. Az persze kérdés, hogy milyen 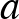 pozitív egészekre létezik megfelelő felbontás. Erre ad választ a következő állítás.
pozitív egészekre létezik megfelelő felbontás. Erre ad választ a következő állítás.
Állítás: Valamely 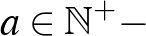 ra
ra 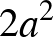 pontosan akkor áll elő két különböző négyzetszám összegeként, ha az
pontosan akkor áll elő két különböző négyzetszám összegeként, ha az 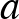 szám prímtényezős felbontásában van
szám prímtényezős felbontásában van 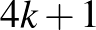 alakú prímszám (
alakú prímszám ( 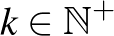 ).
).
Bizonyítás: Felhasználjuk azt a tételt, amely szerint egy négyzetszám pontosan akkor írható fel két kisebb négyzetszám összegeként, ha a prímtényezős felbontásában van 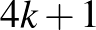 alakú prím. (Ennek bizonyítása a cikk végén megadott hivatkozásban található.)
alakú prím. (Ennek bizonyítása a cikk végén megadott hivatkozásban található.)
Először tegyük fel, hogy az 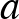 pozitív egész szám prímtényezős felbontásában van
pozitív egész szám prímtényezős felbontásában van 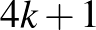 alakú prímszám. Ekkor
alakú prímszám. Ekkor 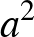 előáll két, nála kisebb négyzetszám összegeként, vagyis valamilyen
előáll két, nála kisebb négyzetszám összegeként, vagyis valamilyen 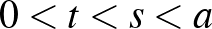 egészekre
egészekre 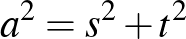 . Ekkor
. Ekkor 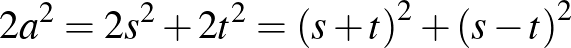 . Nyilván
. Nyilván 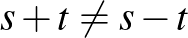 , mert akkor
, mert akkor 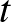 egyenlő lenne 0-val. Így
egyenlő lenne 0-val. Így 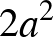 előáll két különböző négyzetszám összegeként.
előáll két különböző négyzetszám összegeként.
Nézzük meg a másik irányt. Tegyük fel, hogy 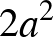 előáll két különböző négyzetszám összegeként, vagyis
előáll két különböző négyzetszám összegeként, vagyis 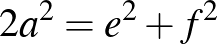 , ahol
, ahol 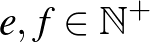 és
és 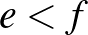 . Ekkor
. Ekkor 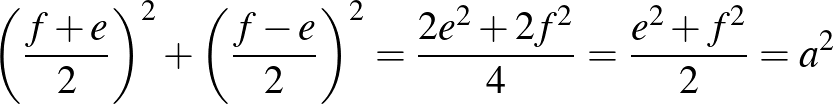 . Mivel
. Mivel 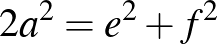 , ezért
, ezért  és
és  azonos paritásúak, és így
azonos paritásúak, és így 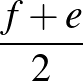 , valamint
, valamint 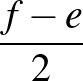 természetes számok. Egyik sem lehet egyenlő 0-val, ezért az
természetes számok. Egyik sem lehet egyenlő 0-val, ezért az 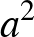 számot előállítottuk két, nála kisebb négyzetszám összegeként. A hivatkozott tétel alapján ez azt jelenti, hogy az
számot előállítottuk két, nála kisebb négyzetszám összegeként. A hivatkozott tétel alapján ez azt jelenti, hogy az 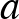 pozitív egész szám prímtényezős felbontásában van
pozitív egész szám prímtényezős felbontásában van 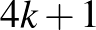 alakú prímszám. Ezzel az állítást beláttuk.
alakú prímszám. Ezzel az állítást beláttuk.
A fenti állításból következik természetesen az is, hogy végtelen sok nemtriviális megoldása van a cikk elején kitűzött problémának. Egyúttal a komplex számoknak egy szép alkalmazását találtuk a másodfokú egyenletek témakörében.
Hivatkozás
- [1] Maga Balázs és Török Mihály: Háromszögszámok és négyzetszámok összegéről
https://magab.web.elte.hu/irasok/szeged
Tritz Árpád
Szegedi Tudományegyetem Gyakorló Gimnázium és Általános Iskola