Mi várható a 2024. májusi érettségin?

A matematika mintafeladatsor didaktikai elemzése a NAT2020 változásainak tükrében

Változások a közoktatásban

A hazai közoktatás egyik alapvető tartalmi szabályozó dokumentuma a Nemzeti Alaptanterv (NAT). Fejlesztése, jóváhagyása központilag koordinált, a benne foglaltak pedig az oktatás minden szereplőjére egyöntetűen vonatkoznak. A NAT-ot ([1]) a Magyar Közlönyben hirdetik ki, és az aktuális kerettanterveket ([2]) is ehhez igazítják. Rendszeres felülvizsgálatának és átdolgozásának köszönhetően a jelenleg hatályban lévő 2020-as változata már az 5. Nemzeti Alaptantervünk az első, 1995-ös megjelenése óta. (A továbbiak 2003-ból, 2007-ből és 2012-ből származnak.)

Az érettségi vizsga követelményeinek minden esetben követnie kell a tantervben eszközölt változtatásokat, így az alaptanterv megjelenésével párhuzamosan szükség volt a részletes érettségi vizsgakövetelmények tárgyanként eltérő fokú átdolgozására. Matematikából az új követelményrendszer bevezetése nem hozott drasztikus változásokat. Általánosságban elmondható, hogy a középszintről kikerülő ismereteket emelt szinten továbbra is kérdezhetik majd, a középszint követelményei pedig pár új elemmel gazdagodtak, a korábbi hangsúlyok némiképp eltolódtak. Ezekre példa az exponenciális egyenletekkel leírható folyamatok modellezése, a megtakarítási és hitelfelvételi lehetőségekkel kapcsolatos pénzügyi számítások elvégzése, valamint a statisztikai ismeretek egy eddiginél jóval szélesebb tárháza.

Az érettségivel kapcsolatos minden hivatalos dokumentum megtalálható az Oktatási Hivatal honlapján. Az idei évtől kezdődően minden érettségizőre egységesen a „Közismereti érettségi vizsgatárgyak 2024. május–júniusi vizsgaidőszaktól érvényes vizsgakövetelményei vonatkoznak ([8]). A régi, 2012-es NAT-ra épülő dokumentumok viszont továbbra is fellelhetők az archív anyagok között ([9]). Szintén itt találjuk a 2024. május–júniusi vizsgaidőszaktól érvényes vizsgakövetelmények szerint készült érettségi mintafeladatokat ([11]). Jelen cikk keretein belül én ezek közül a középszintű matematika feladatsor elemzésével foglalkozom, hiszen egyrészt itt következett be jelentősebb változás, másrészt a korábbi évek tendenciái alapján a matematikából érettségiző diákok átlagosan 90-95%-a a középszintű érettségi vizsgát választja. (Pontos létszámadatok az elmúlt évek érettségi vizsgáiról a www.ketszintu.hu/publicstat.php oldalon érhetők el.)

A témával korábban az Érintőben már foglalkozott Csapodi Csaba 5 részből álló cikksorozata ([3], [4], [5], [6], [7]), amely témakörönként járja körbe az újításokat, valamint mutat pár elképzelhető, új típusú feladatot.

A középszintű matematika érettségi vizsga

Az érettségi vizsgák időpontját a tanév rendjére vonatkozó miniszteri rendelet határozza meg ([10]). Tavasszal a fő tárgyak a 2020-as vészhelyzetben bevezetett intézkedések óta 9 órakor kezdődnek, így a 2024. évi május–júniusi matematika írásbeli érettségi vizsga 2024. május 7-én 9 órakor veszi kezdetét.

Az 5 nagy témakör nem változott (1. Gondolkodási módszerek (20%), 2. Számelmélet, algebra (25%), 3. Függvények (15%), 4. Geometria (25%), 5. Valószínűségszámítás, statisztika (15%)), valamint azok adott feladatsoron belüli hozzávetőleges aránya (zárójelben) sem. Középszinten, a szóbeszédek ellenére, szóbeli vizsgára továbbra is csak abban az esetben kerül sor, ha az írásbeli vizsgán a vizsgázó pontszáma eléri a 12 pontot (a maximális 100 pontból), de az elégséges érdemjegyhez szükséges 25-öt nem, vagy ha mentesül az írásbeli érettségi vizsga alól.

A mintafeladatsorral ([12]) kapcsolatban az egyik legszembetűnőbb változás annak felépítése lehet. A feladatlap szerkezete azonban nem változik 2024-től sem. Az első rész továbbra is 12 rövid, alapösszefüggésekre irányuló, jellemzően csak a végeredmény közlését kérő feladatot fog tartalmazni. Ezt a második rész szintén módosítás nélkül követi; vagyis három kötelező példa lesz a 15. feladatig bezárólag, az utolsó három közül pedig továbbra is csak kettő tetszőlegesen választottat kell majd megoldani, a kihagyott feladat sorszámát pedig az erre a célra fenntartott helyen jelölni. Amennyiben ez nem történik meg, és a választás ténye a dolgozatból sem derül ki egyértelműen, akkor automatikusan az utolsó feladat nem kerül értékelésre. Itt hosszabb, több részfeladatból álló feladatok találhatók, amelyek esetében már az eredményhez vezető lépések adják a pontszám döntő részét, maga a megoldás, illetve esetenként annak ellenőrzése csupán 1-1 pontot ér.

Segédeszközként továbbra is használható többek között bármilyen szöveges adatok tárolására és megjelenítésére nem alkalmas számológép, valamint a négyjegyű függvénytáblázat tetszőleges példánya, egyidejűleg akár több is.

Érettségi 2024: A mintafeladatsor elemzése

Első rész

A halmazok, gráfok és kombinatorika témaköréből származó első három feladat jellege a korábbiakkal teljes egyezést mutat, hiszen itt a követelményrendszerben sem történt jelentős változás. A logikai szita elve implicite eddig is megjelent a halmazos feladatokban, mostantól azonban fel kell készíteni a diákokat arra, hogy ezt az ismeretet tudatosan használják. Ehhez támpontot szolgáltathat [3, 1.6. feladat].

Bevették a gráf csúcsainak fokszámösszege és az éleinek száma közti összefüggés ismerete mellé annak alkalmazását a gyakorlatban, ez azonban csak formai finomítás, hiszen ezt az ismeretet korábban is számon kérték a gráfokkal modellezhető feladatoknál.

Feladat. Írja fel a 2021-et 8-as számrendszerben!

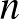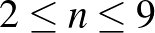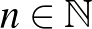Ez a feladat abszolút újszerű. Míg korábban középszinten csak a kettes és tízes számrendszer közti átváltások jelentek meg, és inkább csak az idegen nyelvű feladatsorokban, addig az új követelményrendszer már elvárja az áttérés módjának ismeretét a 10-es és bármely $n$ alapú számrendszer között, ahol $2 \leq n \leq 9$ , $n \in \mathbb{N}$ .

Napjainkban a számrendszerek az informatikában és a számítástechnikában fontos szerepet játszanak. Itt a bináris, oktális és hexadecimális számrendszereket használják. Az, hogy a mintafeladatsorban épp a 8-as számrendszer jelenik meg, lehet puszta véletlen, de a 2021 szám használata már bizonyosan tudatos volt, a feladatokat ugyanis ebben az évben publikálták. Talán érdemes lehet a számrendszerek közötti átváltás gyakoroltatásánál feladni a 2024-es számot.

Feladat. Egy mértani sorozat második tagja 2, negyedik tagja 4. Adja meg a sorozat hatodik tagját! Válaszát indokolja!

A mértani, vagy éppen számtani sorozat 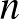$n$ -edik tagjára vonatkozó feladattípus szintén ismert. Bár az általános tag felírása a kis indexeknek köszönhetően itt mellőzhető, a tapasztalataim azt mutatják, hogy a diákok mégis előszeretettel választják a képletbe helyettesítést a „lépkedés” helyett.

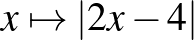Feladat. Ábrázolja az $[1; 4]$ zárt intervallumon értelmezett $x \mapsto \vert 2x-4\vert$ függvényt!

Az abszolútérték-függvény, néhány egyéb függvénnyel együtt, átkerült középről emelt szintre, a függvénytranszformációknál viszont új elemként megjelenik az 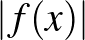$\vert f(x)\vert$ . Ez szerepel is a 8. példában, ahol a feladat egy korlátos, zárt intervallumon értelmezett függvény ábrázolása. Ilyen formában nem csupán egy lineáris, hanem egy tetszőleges másodfokú, a 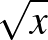$\sqrt x$ , az $\frac{1}{x}$ , vagy akár egy exponenciális függvény abszolútértékét is számon lehet kérni.

Feladat. Adja meg az 1, 1, 2, 2, 3, 3, 3, 5 minta alsó és felső kvartilisét!

Az egyik legjelentősebb változáson átesett témakör a statisztika, összhangban a XXI. századi adatvezérelt társadalmunkkal. A rövid feladatrészben az eddig megszokott statisztikai mutatók, úgymint középértékek (átlag, módusz, medián) és szóródási mérőszámok (terjedelem, szórás) mellett megjelennek a kvartilisek (negyedelők), viszont kikerül a súlyozott számtani közép és az átlagos abszolút eltérés. A fenti feladat éppen a kvartilisek kiszámítását kívánja meg egy 8 adatot tartalmazó mintából. Mivel meghatározásukra nincs egységes megállapodás, a táblázatkezelő programokkal vagy a különböző számológépekkel kapott értékek eltérhetnek a tanórán tanultaktól. Bár nagy számú adat esetén ez a különbség irreleváns, fontos, hogy a tantervben szereplő módon számítsuk őket. Ehhez először nagyság szerint növekvő sorba rendezzük az adatokat, majd páros elemszám esetén a mediánnal kettéosztott két részsokaságnak külön-külön vesszük a mediánját, páratlan elemszámnál pedig kettéosztás után a mediánt elhagyva tesszük ugyanezt.

Nem tisztázott kérdés viszont, hogy a kvartilisek kiszámítására további matematikai indoklás nélkül használhatók-e a számológépek, ahogyan az átlag és a szórás esetén. Megjegyzendő továbbá, hogy bár a feladat mintát említ, középszinten a tanulóktól nem elvárt, hogy tisztában legyenek a sokaság és az abból vett minta fogalmával és a köztük levő különbözőséggel.

Feladat. Egy hegyesszög koszinusza 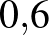$0{,}6$ . Mennyi a kiegészítő szögének a koszinusza?

Fontosnak tartom felhívni a figyelmet arra is, hogy bár a szögfüggvények általános definíciója, a negatív szögekre vonatkozó összefüggések és a trigonometrikus egyenletek szintén átkerültek emelt szintre, középszinten továbbra is elvárt a szögfüggvény értékének ismeretében a szög visszakeresése (számológéppel), valamint meg kell tudni határozni tompaszögek szögfüggvényeit is a kiegészítő szögük szinuszának/koszinuszának ismeretében. Erre a szinusztétel kapcsán különösen nagy szükség lehet, noha az érettségin nem jellemző olyan feladat, ahol a megadott feltételeknek egy hegyes-, illetve egy tompaszögű háromszög egyaránt eleget tenne. Úgy gondolom, hogy ez a változtatás nagy könnyebbség lehet a tanulók számára, hiszen a tapasztalatok azt mutatják, hogy a valós számok halmazán értelmezett trigonometrikus egyenletek megoldását a többségnek nem sikerül megfelelően elsajátítania. Szintén nagy terhet vesz le a vállukról az, hogy a szögeket csak fokokban kell mérni, mivel az ívmérték (radián) átkerült emelt szintre.

Egy másik számottevő változáson átesett témakör a koordinátageometria. A továbbiakban nincs szükség sem a szakasz harmadolópontjának, sem pedig a háromszög súlypontjának meghatározására. A középszinten megmaradt az egyenes 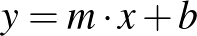$y=m \cdot x+b$ (és az 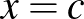$x=c$ ) alakban megadott egyenletének ismerete, az ettől különböző felírásai azonban átkerültek emelt szintre. Vagyis elvárható a két adott ponton átmenő egyenes egyenletének meghatározása, ami szerepel is a feladatsorban. A pontok koordinátáit a fenti alakba behelyettesítve, egy egyenletrendszer megoldásaként kapjuk meg a meredekséget és az 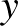$y$ tengelymetszetet.

Szintén számonkérhető a fenti alak kizárólagos ismerete mellett az egyenes meredeksége és az egymással párhuzamos, illetve egymásra merőleges egyenesek meredekségére vonatkozó összefüggések. Jóllehet a normálvektoros vagy az irányvektoros alak már egyáltalán nem követelmény, ettől függetlenül a tapasztalataim szerint sok helyen még a mai napig tanítják őket.

A kör egyenletének felírása csak a középpont és a sugár (esetleg az átmérő, vagy annak két végpontjának) ismeretében kerülhet elő, ezek visszakeresése a kétismeretlenes másodfokú egyenletből már nem elvárás többé (a teljes négyzettá alakítás módszerét ettől függetlenül továbbra is ismerni kell). Nem kell tudni meghatározni kör és egyenes metszéspontját, ahogyan a kör adott pontjához húzott érintő egyenletét sem.

A 12. feladat nem meglepő módon egy valószínűségszámítási példa. Az e témakörhöz tartozó ismeretek sora jelentősen bővült, tudni kell ezentúl a következőket: elemi esemény, események összege, szorzata, adott esemény komplementere, továbbá egymást kizáró és független események. Bár a feladat független események együttes bekövetkezésének valószínűségének a kiszámítását kívánja meg, megoldható a klasszikus kombinatorikus modellel is. A megoldókulcs itt mindkét megközelítést közli.

Második rész

Általában a 13. feladatban valamilyen egyenlet, egyenlőtlenség vagy egyenletrendszer szokott szerepelni. Nincs ez másképp a mintafeladatsorban sem, ahol egy egyszerű exponenciális egyenlet megoldásával 5 pont szerezhető az a) részben. A megoldókulcsban szemet szúrhat, hogy a helyes 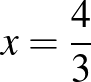$x=\frac{4}{3}$ eredmény közlése helyett kerekített érték esetén nem adható meg a megoldásért járó 1 pont. Ez annak fényében különös, hogy korábban a javítókulcs úgy rendelkezett, hogy amennyiben „egy feladat szövege nem ír elő kerekítési kötelezettséget, akkor az útmutatóban megadottól eltérő, észszerű és helyes kerekítésekkel kapott rész- és végeredmény is elfogadható” legyen. Szintén nem világos, hogy az eredmény ellenőrzése továbbra is kiváltható-e az alaphalmaz vizsgálatával és az ekvivalens átalakításokra való hivatkozással. Ezért inkább minden esetben azt javasoljuk, hogy a megoldás helyességét az eredeti egyenletbe visszahelyettessítéssel ellenőrizzük.

Az egyenlet valóstól eltérő alaphalmazát a 13. b) feladatban vastag betűvel emelték ki. Ezt figyelemfelkeltés gyanánt hasznosnak tartom.

A 14. feladat komplexebb statisztikai ismereteket kér számon. A feladat egy box-plot (más néven doboz-, vagy sodrófa-) diagram értelmezése, amely teljesen új elem, csakúgy, mint a rá vonatkozó állítások igazságértékének eldöntése. A következő szint az adott adatok ábrázolásához leginkább megfelelő diagramtípus kiválasztása és a választás indoklása lenne. Ez a követelményrendszerben már ugyan megjelenik, ugyanakkor úgy gondolom, hogy az eddig számonkért statisztikai ismeretekhez képest ez túl nagy ugrás lenne. A grafikus manipulációk felismerése és javítása grafikonok esetében külön említést érdemel, gyakorlati haszna megkérdőjelezhetetlen, ám ez is egyelőre csak a követelményrendszerbe került bele, a mintafeladatok szintjén még nem találkoztunk vele. (A [7] cikk azonban tartalmaz ilyen feladatokat, ezeket mindenképpen érdemes megnézni. A megoldásuk az Érintő Facebook-oldalán jelenik majd meg. A szerkesztő megjegyzése.)

Középszinten innentől kezdve követelményként jelenik meg az egyszerű állítások, tételek bizonyítása, úgymint a hatványozás azonosságai konkrét alap és pozitív egész kitevő esetén, számtani és mértani sorozat első 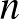$n$ tagjának összegére vonatkozó képletek, a háromszög oldalfelező merőlegesei, illetve a belső szögfelezők metszéspontjára vonatkozó tételek, Pitagorasz-tétel, sokszögek átlóinak számára, a belső- és külső szögeiknek összegére vonatkozó összefüggések, Thalész-tétel vagy a szinusztétel, amelyek azonban egyelőre kizárólag a szóbeli vizsgán jelennek majd meg.

A „bizonyítsa” kifejezés szerepel a 15. feladatban, amely komolyabb hangzása miatt elsőre talán ijesztően hathat. Problémát okozhat, ha a tanuló nincs tisztában azzal, hogy mit várunk tőle bizonyítás címszó alatt, netán túlgondolja annak mélységét, és emiatt esetleg egyáltalán nem is próbálkozik a feladat megoldásával. Érdemes tehát az alábbiak tudatosítása.

A bizonyítandó állításokon a „Mutassa meg”, „Igazolja” típusú bizonyításokat kell érteni, amelyek mellett ezentúl megjelenik a korábban szándékosan mellőzött „Bizonyítsa” szó is, ám ez továbbra is inkább az eredmény igazolását számítással, logikus érveléssel fogja jelenteni az írásbeli vizsgán, mintsem deduktív bizonyítást. Az állítás maga a matematika szinte bármely területéről származhat, várhatók például geometriai, számelméleti kijelentések. (Erre példákat [3]-ban érdemes nézni.)

Szintén új elem a várható érték megjelenése az emelt mellett középszinten. A 16. feladat egy fiktív nyereményjáték részleteit tartalmazza, amely 300 Ft-os eladási áron kínál eltérő nyereményű sorsjegyeket, a kérdés pedig a cég egy sorsjegyre jutó nyereségének várható értéke. Könnyítésképpen a szövegből is kinyerhető, mit értünk nyereségen. Az ehhez szükséges kiadások kiszámítása történhet a nyereményértékek valószínűségeivel (relatív gyakoriságokkal) súlyozott átlagaként, vagy számolhatunk a táblázatban szereplő gyakoriságokkal, ez esetben a sorsjegyek darabszámával a számolás végén kell osztani.

Az, hogy a jövőben a megtakarítási, befektetési és hitelfelvételi lehetőségekkel és azok kockázati tényezőivel kapcsolatos feladatokra a tananyagban és a számonkérésben egyaránt számítani kell, mind a pénzügyi tudatosságra nevel. A kamatos kamatszámítási feladatok mellett így a gyűjtőjáradék és törlesztőrészlet meghatározása is alapvető jelentőségű lesz.

Mindkét feladattípus begyakorlásához a korábbi évek emelt szintű feladatsorai jó mankót jelenthetnek, vagy inspirálódhatunk innen: [5]. Előbbiről akkor beszélünk, ha egyenlő időközönként ugyanakkora összeggel növelünk egy kiindulási értéket, vagyis például egy bankban vezetett megtakarítási számlánkra évente mindig azonos összeget fizetünk be, ahol így minden befizetésünkre kamatos kamatot számolnak fel. A törlesztőrészlet esetében pedig a felvett hitelt fizetjük vissza szintén azonos időközönként és egyenlő részletekben, a fennálló hiteltartozásunkat, amelyre szintén kamatos kamatot terhelnek, így fokozatosan csökkentve.

Értékelésük, megfelelő pontozásuk azonban annál alaposabb megfontolást kíván meg, mint ahogy az ebben a mintafeladatsorban szerepel.

A 17. feladat b) részében 7 pont szerezhető a gyűjtőjáradék helyes kiszámításával, amely a függvénytáblázatban szereplő képletbe helyettesítéssel megoldva egész biztosan nem a feladat kitűzőjének eredeti szándékát szolgálja. Bár a feladatra adható pontszám jelentős hányada a gondolatmenetre, nem pedig a kapott eredményre jár, és kiemelt jelentőségű a részszámítások nyomonkövethetősége, mindenféleképpen felmerül a kérdés, hogy a függvénytáblázatban található képlet indoklás nélkül átemelhető-e. Maga a feladat a következő:

Feladat. Dóri szülei elhatározzák, hogy most született gyermekük felsőoktatási tanulmányainak fedezésére 18 éven keresztül minden év elején elhelyeznek 100 000 Ft-ot a fenti kamatfeltétellel (évi 4%-os kamat) egy számlára.

b) Mutassa meg, hogy ilyen módon a 18. év végére több mint 2 600 000 Ft lesz a számlán!

Az 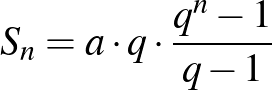$S_{n}=a \cdot q \cdot \frac{q^{n}-1}{q-1}$ képletbe való behelyettesítés pedig pont az 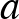$a$ járadéknak az 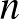$n$ -edik év végére felnövekedett étékét adja meg, amennyiben a befizetések az év elején történnek.

Feladat. Dóri egyetemi évei alatt tanulmányai költségeire szeretne felhasználni az összegyűlt pénzből 2 600 000 Ft-ot. Azt tervezi, hogy hat éven keresztül minden év elején ugyanakkora összeget vesz fel egy olyan számláról, amelyen kezdetben ez az összeg szerepel (a számlán maradó összeg továbbra is minden év végén 4%-ot kamatozik). Az a célja, hogy amikor a hatodik év elején felveszi az adott összeget, akkor pont elfogyjon a számláról a 2 600 000 Ft.

c) Mekkora összeget vegyen fel Dóri minden év elején, hogy a célja teljesüljön? Válaszát száz forintra kerekítve adja meg!

A fenti példa felfogható egy fordított hitelkonstrukcióként is, amikor is Dóri pénze van a banknál, és a pénzintézet azt „törleszti” számára évente azonos összegekben. Arra kell csak figyelnünk, hogy míg a hiteltörlesztés rendszerint az adott periódus végén történik addig itt év elején csökken a fennálló tartozás mindig 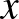$x$ összeggel, ez azonban nem jelent lényegi különbséget. A folyamat tehát egy az egyben egy olyan hitelfelvételnek feleltethető meg, ahol a kiindulási összeg 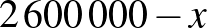$2\,600\,000-x$ , és így éppen az 5. év végére (a 6. év elejére) merül ki a keret.

Bár ez a gondolatmenet szintén képes kiváltani a folyamat évről évre történő nyomonkövetését, az analógiára való hivatkozás a témakör olyan szintű ismeretét, összefüggéseinek átlátását kívánja meg, hogy ezért véleményem szerint már jogosan ítélhető oda a feladatért járó 7 pont teljes egésze.

A feladat kitűzőjének ugyanakkor eredeti szándéka egyértelműen az lenne, hogy a diák modellezze a pénz útját az első időszaktól kezdve bizonyos számú köztes időszakot átugorva az utolsóig bezárólag, valamint ismerje fel, hogy az így kapott összeg egy része éppen egy mértani sorozat első 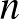$n$ tagjának összege, amelyre így alkalmazható az összegképlet. Mindez azonban megkerülhető a függvénytáblázatban található képletekbe helyettesítéssel. Ebből pedig nem derül ki, hogy tudatosan használja-e a diák a képletet, ezt nehéz utólag ellenőrizni.

Bár a függvénytáblázatok terén a jövőben változásokra számíthatunk ([14]), a témakörrel kapcsolatban nem pusztán a kitűzhető feladatok köre érdemel említést, hanem a hozzájuk kapcsolódó, a függvénytáblázatban fellelhető képletek is. A „fehér” függvénytáblázatban 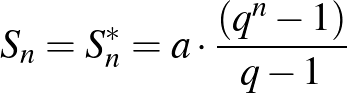$S_n=S_n^{*}=a \cdot \frac{(q^n-1)}{q-1}$ képlet adja meg az 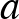$a$ járadéknak az 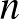$n$ -edik év végére felnövekedett értékét, amennyiben a befizetés minden év végén esedékes. Ugyanerre az 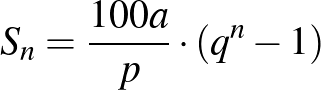$S_n=\frac{100a}{p}\cdot(q^n-1)$ képlet is szerepel, amely az előzőből adódik a 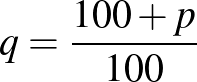$q=\frac{100+p}{100}$ helyettesítéssel. Félrevezető lehet a 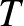$T$ hitel évente azonos összegben megfizetett törlesztőrészletére vonatkozó képlet (év végi törlesztés esetén)

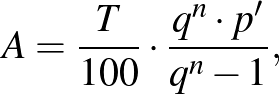
$\displaystyle A=\frac{T}{100} \cdot \frac{q^n\cdot p'}{q^n-1},$

amelyben 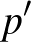$p'$ helyett 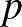$p$ -nek kellene szerepelnie. A „sárga” függvénytáblázatban ez a képlet helyesen van benne, és emellett a 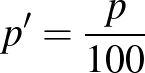$p'=\frac{p}{100}$ összefüggés is megjelenik.

A függvénytáblázatok eltérő képletei szólhatnak amellett, hogy a feladatok helyes megoldása pusztán a képletekbe való behelyettesítéssel valóban nem kapható meg, a megoldást azonban sokkal inkább olyan feladatok kitűzése jelentené, amelyek komplexitásukból adódóan ennél többet kívánnak meg.

Megjegyezném, hogy a jelenleg forgalomban lévő függvénytáblázatok („fehér” és „sárga”) használata kellő gyakorlat hiányában értékes, elvesztegetett perceket jelenthet a diák számára a vizsgán. Éppen ezért fontos lehet ezek előzetes áttanulmányozása, a birtokolt ismeretek matematikán belül elfoglalt helyének, a témaköröknek a beazonosítása.

A 18. feladat mindössze a) és b) részeket tartalmaz. Az elmúlt évek feladatsorai struktúrájának tükrében ez meglehetősen szokatlan, inkább a kétszintű érettségi vizsga kezdeti időszakát jellemezték a nagyobb pontértékű, kevesebb, egymással összefüggő részekből álló feladatok. A tagoltság és a megoldhatóság szempontjából való függetlenség – ami 2017 óta elvárás – mellett szól az, hogy ily módon egy-egy jó gondolat meglétén, vagy éppen hiányán nem múlik túl sok pont, és az esetleges elkövetett hibák nem öröklődnek.

Középszinten teljesen új anyag a geometriai valószínűség, amikor az elemi eseményeket egy geometriai alakzat pontjaihoz rendeljük hozzá, azt feltételezve, hogy az eseményhez tartozó ponthalmaz mértéke (pl. a hossza, a területe, illetve a térfogata egy, két és három dimenzióban) egyenesen arányos az esemény valószínűségével, amely ily módon megkapható a részhalmaz és a teljes alakzat mértékének a hányadosaként. Egyik klasszikus példája a céltáblára lövés, ahol magát a céltáblát 1 valószínűséggel eltaláljuk, a klasszikus modell esetében megszokottól eltérő módon azonban 0 valószínűség tartozik a tábla egy adott pontjának eltalálásához, amely azonban korántsem lehetetlen esemény.

Az eseménytér végtelen, ez szemben áll az eddig ismert diszkrét esetekkel. A geometriai valószínűség tehát a valószínűségi változó fogalmának bevezetése és az eloszlások csoportosításának ismerete nélkül biztosít lehetőséget a folytonosság kezelésére. Jelentősége miatt éppen ezért úgy vélem, hogy a végleges feladatsorban nem a kihagyható példák között lenne a helye, komplexitása pedig indokolná, hogy egyszerűbben, kevesebb pontértékkel és kisebb kockázattal járó feladatként jelenjen meg a bevezetése utáni első években. Jóllehet, hogy itt a 8-ból 6 pont a térgeometriai számításokra jár, de az új ismeret hiányában elképzelhető, hogy ezeknek a tanuló neki sem kezd.

A geometriai valószínűség valódi ereje azonban abban rejlik, hogy olyan problémákra alkalmazzuk, amelyek alapvetően nem geometriai jellegűek. A későbbiekben éppen ezért fontosnak tartanám a geometriai objektumok mellett az azoktól való elrugaszkodást, és például annak a valószínűségének kiszámítását, hogy amennyiben 12:30-kor érünk a megállóba, elérjük a buszt, ami egy véletlenszerű időpontban érkezik dél és délután 1 óra között.

További megjegyzések

A logaritmus „kikerülésének” híre sokakat felvillanyozott, hiszen a nehezen emészthető anyagrészek közé tartozott. A félreértések elkerülése végett, a logaritmus definíciójának és fogalmának ismeretére továbbra is szükség van, csupán az azonosságok és a tízestől eltérő alapra való áttérés vált emelt szintű ismeretanyaggá. Középszinten ehelyett megjelenik a tetszőleges alapú logaritmus értékének kiszámítása tízes alapú logaritmussal. Mindkét irányú változást üdvözölni lehet. Egyfelől lényeges, hogy tisztában legyenek a diákok a tízes alapú logaritmus jelentőségével a szám nagyságrendjének meghatározásában, tudják, hogy megkapható általa a kérdéses szám számjegyeinek száma. (Vonatkozott is erre feladat 2019 májusában az idegen nyelvű feladatsorban.) Másfelől a zsebszámológépek megjelenése és elterjedése mára már teljesen kiszorította a logaritmustáblázatok használatát, a mai számítási kapacitások mellett már felesleges a szorzás és osztás visszavezetése összeadásra, illetve kivonásra logaritmussal. A hatványkitevőre vonatkozó azonossággal azonban elképzelhető, hogy továbbra is számolni kell, hiszen az megjelenhet az exponenciális folyamatok modellezésében, amelyek 2024-től is várhatóan a középszintű feladatsorok állandó szereplői lesznek.

Azokhoz a követeleményrendszerbeli változásokhoz, amelyekre a mintafeladatsorban nem találunk példát, jó mankót jelenthet a [13] dokumentum, amely tételesen listázza a legfontosabb középszinten megjelenő új ismereteket és az egyik szintről a másikra átkerülő fogalmakat egyaránt. A bevezetőben említett Érintőben megjelent öt cikkből álló sorozat pedig a változások ismertetése mellett további konkrét feladatokkal biztosít a diákok számára ingyenes, akár önálló gyakorlási lehetőséget.

Mivel a mintafeladatsor az újdonságok ellenére is nagyfokú egyezést mutat a korábbi évekével, így a felkészülés egyik további, de nem kizárólagos módja lehet az elmúlt évek középszintű érettségijeinek, az emelt szintről lekerülő témakörök esetében pedig a korábbi emelt írásbeli vizsgák megfelelő feladatainak megoldása.

Irodalomjegyzék

[1] Magyar Közlöny 2020. évi 17. szám. https://magyarkozlony.hu/dokumentumok/3288b6548a740b9c8daf918a399a0bed1985db0f/megtekintes. (Letöltve: 2024. január 25.)

[2] A 2020-as NAT-hoz ill. tartalmi szabályozók. https://www.oktatas.hu/kozneveles/kerettantervek/2020_nat. (Letöltve: 2024. január 25.)

[3] Csapodi Csaba, A matematika érettségi követelményeinek változása 2024-től – I. rész, Érintő, 2023. március, 27. szám. https://ematlap.hu/tanora-szakkor-2023-3/1318-a-matematika-erettsegi-kovetelmenyeinek-valtozasa-2024-tol-iii-resz. (Letöltve: 2024. január 25.)

[4] Csapodi Csaba, A matematika érettségi követelményeinek változása 2024-től – II. rész, Érintő, 2023. június, 28. szám. https://ematlap.hu/tanora-szakkor-2023-2/1284-a-matematika-erettsegi-kovetelmenyeinek-valtozasa-2024-tol-ii-resz. (Letöltve: 2024. január 25.)

[5] Csapodi Csaba, A matematika érettségi követelményeinek változása 2024-től – III. rész, Érintő, 2023. szeptember, 29. szám. https://ematlap.hu/tanora-szakkor-2023-3/1318-a-matematika-erettsegi-kovetelmenyeinek-valtozasa-2024-tol-iii-resz. (Letöltve: 2024. január 25.)

[6] Csapodi Csaba, A matematika érettségi követelményeinek változása 2024-től – IV. rész, Érintő, 2023. december, 30. szám. https://ematlap.hu/tanora-szakkor-2023-4/1343-a-matematika-erettsegi-kovetelmenyeinek-valtozasa-2024-tol-iv-resz. (Letöltve: 2024. január 25.)

[7] Csapodi Csaba, A matematika érettségi követelményeinek változása 2024-től – V. rész, Érintő, 2024. március, 31. szám. https://ematlap.hu/tanora-szakkor-2024-5/1367-a-matematika-erettsegi-kovetelmenyeinek-valtozasa-2024-tol-v-resz. (Letöltve: 2024. március 10.)

[8] Közismereti érettségi vizsgatárgyak 2024. május–júniusi vizsgaidőszaktól érvényes vizsgakövetelményei. https://www.oktatas.hu/kozneveles/erettsegi/kozismereti_vizsgatargyak_2024tol. (Letöltve: 2024. január 25.)

[9] Közismereti érettségi vizsgatárgyak 2023. október-novemberi vizsgaidőszakig érvényes vizsgakövetelményei. https://www.oktatas.hu/kozneveles/erettsegi/kozismereti_vizsgatargyak_2023ig. (Letöltve: 2024. január 25.)

[10] A 2024. évi május–júniusi írásbeli érettségi vizsgák időpontjai. https://www.oktatas.hu/pub_bin/dload/kozoktatas/erettsegi/2024/ vizsgaidopontok_2024maj_jun.pdf. (Letöltve: 2024. január 25.)

[11] Mintafeladatok a 2024. május–júniusi vizsgaidőszaktól érvényes vizsgakövetelmények szerint. https://www.oktatas.hu/kozneveles/erettsegi/mintafeladatok_2024. (Letöltve: 2024. január 25.)

[12] Matematika középszintű írásbeli érettségi vizsga mintafeladatsor. https://www.oktatas.hu/pub_bin/dload/kozoktatas/erettsegi/vizsgakovetelmenyek2024/mintafeladatok_2024/mat_kozep_irasbeli_minta.pdf. (Letöltve: 2024. január 25.)

[13] Csapodi Csaba, Az érettségi követelmények változása 2024-től. https://nemzetipedkar.hu/wp-content/uploads/2023/12/nat-2020-erettsegi-valtozasai.pdf. (Letöltve: 2024. március 8.)

[14] Wintsche Gergely: Kell-e nekünk függvénytáblázat? Érintő, 29. szám 2023. szeptember. https://ematlap.hu/tanora-szakkor-2023-3/1301-kell-e-nekunk-fuggvenytablazat. (Letöltve: 2024. március 8.)

Geszler Evelin Anna,

az ELTE Matematika Doktori Iskola
didaktika programjának végzős doktorandusz hallgatója