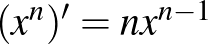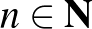A cikksorozat második részében közölt feladatok megoldása itt található. A harmadik rész a függvények témakörének változásairól szól. Először bemutatjuk az érettségi követelmények változását táblázatos formában. A táblázatban (piros színnel) jelezzük az újonnan megjelenő követelményeket és a törölt ismereteket is. (Ha egy követelmény átkerült középszintről emelt szintre, akkor azt csak a középszinten jelöljük kihúzással és emelt szinten nem pirosítottuk ki, hiszen eddig is része volt az emelt szintű követelményeknek.) A táblázat után a legfontosabb változásokat röviden megmagyarázzuk, értelmezzük, indokoljuk. Ezután néhány, újdonságnak számító ismeret esetén mutatunk olyan feladatokat, amelyeket a követelmények alapján el tudnánk képzelni egy feladatsorban. Hangsúlyozzuk, hogy ezek személyes elképzelések, az érettségi feladatokat összeállító bizottság nyilvánvalóan saját ötletei és szakmai meggyőződése szerint fog dolgozni.
3. Függvények
| TÉMÁK | VIZSGASZINTEK | |
| Középszint | Emelt szint | |
| 3.1 A függvény | Ismerje a függvény matematikai fogalmát és az alapvető függvénytani fogalmakat (értelmezési tartomány, hozzárendelés, képhalmaz, helyettesítési érték, értékkészlet). Tudjon szövegesen megfogalmazott függvényt képlettel megadni. Tudjon helyettesítési értéket számítani, illetve tudja egyszerű függvények esetén 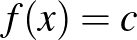 alapján az alapján az 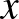 -et meghatározni. Ismerje a kölcsönösen egyértelmű megfeleltetés fogalmát. Ismerje és alkalmazza a függvényeket gyakorlati problémák megoldásánál. -et meghatározni. Ismerje a kölcsönösen egyértelmű megfeleltetés fogalmát. Ismerje és alkalmazza a függvényeket gyakorlati problémák megoldásánál. Ismerje az inverzfüggvény fogalmának szemléletes értelmezését (pl. az exponenciális és a logaritmus függvény vagy a geometriai transzformációk esetében). Tudjon kölcsönösen egyértelmű hozzárendelést megfordítani, és a megfordított hozzárendelést ábrázolni. |
Ismerje az alapvető függvénytani fogalmak pontos definícióját. Ismerje és alkalmazza a függvények összegének, különbségének, szorzatának és hányadosának a fogalmát. Ismerje és alkalmazza a függvények megszorításának (leszűkítésének) és kiterjesztésének fogalmát. I smerje és alkalmazza az inverzfüggvény fogalmát. Ismerje az összetett függvény fogalmát, képzésének módját. |
| 3.2 Egyváltozós valós függvények | Ismerje, tudja ábrázolni és jellemezni az alábbi hozzárendeléssel megadott függvényeket: 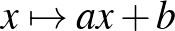 , , 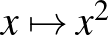 , ,  , , 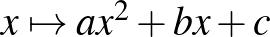 , , 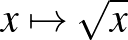 , ,  , ,  , ,  , ,  , ,  , , 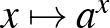 , ,  . . |
Ismerje, tudja ábrázolni és jellemezni az alábbi hozzárendeléssel megadott függvényeket: 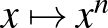 ( ( 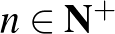 ), ), 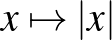 , , 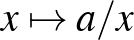 , , 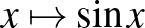 , , 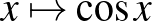 , , 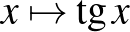 , , 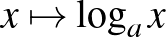 . Tudjon a felsorolt függvényekből összetett függvényeket képezni. . Tudjon a felsorolt függvényekből összetett függvényeket képezni. |
| 3.2.1 A függvények grafikonja, függvénytranszformációk | Tudjon értéktáblázat és képlet alapján függvényt ábrázolni, illetve adatokat leolvasni a grafikonról. | Tudja ábrázolni az alapvető függvények (3.2) transzformáltjainak grafikonját ( 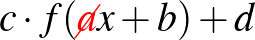 , illetve , illetve 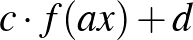 ). ). |
|
Tudjon néhány lépéses transzformációt igénylő függvényeket függvénytranszformációk segítségével ábrázolni: |
||
| 3.2.2 A függvények jellemzése | Tudjon egyszerű függvényeket jellemezni grafikon alapján értékkészlet, zérushely, növekedés, fogyás, szélsőérték, periodicitás, paritás szempontjából. | Tudja jellemezni a függvényeket periodicitás, paritás, korlátosság szempontjából. Tudja meghatározni a függvények tulajdonságait az alapfüggvények ismeretében, transzformációk segítségével. Ismerje és alkalmazza a konvexitás és konkávitás fogalmát. Tudjon másodfokú függvényre vezető szélsőérték-feladatokat megoldani. |
| 3.3 Sorozatok | Ismerje a számsorozat fogalmát és használja a különbözőmegadási módjait (utasítás, képlet, rekurzív definíció). | Tudjon sorozatot jellemezni (korlátosság, monotonitás). Ismerje a konvergencia szemléletes fogalmát, valamint ismerje és alkalmazza egyszerű sorozatokban a konvergens sorozat definícióját. Alkalmazza egyszerű sorozatokban a konvergenssorozatok összegének, különbségének, szorzatának és hányadosának határértékére vonatkozó tételeket. |
| 3.3.1 Számtani és mértani sorozatok | Ismerje a számtani és a mértani sorozat általános tagjára vonatkozó összefüggéseket. Bizonyítsa a számtani és a mértani sorozat összegképletét. Tudjon olyan feladatokat megoldani a számtani és mértani sorozatok témaköréből, ahol a számtani, illetve mértani sorozat fogalmát és az 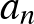 -re, illetve az -re, illetve az 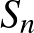 -re vonatkozó összefüggéseket kell használni. -re vonatkozó összefüggéseket kell használni. |
Vezesse le a számtani és a mértani sorozat általános tagjára vonatkozó összefüggéseket. |
| 3.3.2 Végtelen mértani sor | Ismerje és alkalmazza egyszerű feladatokban a végtelen mértani sor fogalmát, összegét. | |
| 3.3.3 Kamatos kamat, járadékszámítás | Tudja a kamatos kamat számítására vonatkozó képletet használni, s abból bármelyik ismeretlen adatot kiszámolni. Tudjon gyűjtőjáradékot és törlesztőrészletet számolni. Tudjon megtakarítási, befektetési és hitelfelvételi lehetőségekkel és azok kockázati tényezőivel kapcsolatos feladatokat megoldani. |
|
| 3.4. Az egyváltozós valós függvények analízisének elemei | ||
| 3.4.1 Határérték, folytonosság | Ismerje a végesben vett véges, a végtelenben vett véges és a tágabb értelemben vett határérték szemléletes fogalmát. Ismerje a folytonosság szemléletes fogalmát. |
|
| 3.4.2 Differenciálszámítás |
Tudja a differencia- és differenciálhányados definícióját. Alkalmazza az összeg-, a különbség-, a konstansszoros, a szorzat- és a hányadosfüggvény deriválási szabályait. Alkalmazza egyszerű esetekben az összetett függvény deriválási szabályát. Tudja bizonyítani, hogy Ismerje a trigonometrikus függvények deriváltját. Alkalmazza a differenciálszámítást érintő egyenletének felírására, szélsőérték-feladatok megoldására és polinomfüggvények vizsgálatára (monotonitás, szélsőérték, konvexitás). |
|
| 3.4.3 Integrálszámítás | Ismerje folytonos függvényekre a határozott integrál szemléletes fogalmát és tulajdonságait. Ismerje a kétoldali közelítés módszerét, az integrálfüggvény fogalmát, a primitív függvény fogalmát, valamint a Newton–Leibniz-tételt. Tudja polinomfüggvények, illetve a szinusz és koszinusz függvény grafikonja alatti területet kiszámolni. | |
Mint látható, kevés érdemi változás történt ebben a témakörben. Kikerült a középszintű követelmények közül az inverzfüggvény fogalma és több függvénytípus, valamint a periodicitás és a paritás fogalma. (Az abszolútérték-függvénnyel kapcsolatos változásról alább részletesen is írunk.) Emelt szinten a konvexitás alkalmazása jelent újdonságot a követelményekben. Középszinten valódi újdonságot a gyűjtőjáradék és a törlesztőrészlet számolásának követelménye jelent.
Az abszolútérték-függvénnyel kapcsolatos változás (ami a többi változáshoz hasonlóan a kerettantervi követelmények változásából fakad) több kollégában kérdéseket vetett fel. Egyfelől kikerült a követelmények közül az  függvény ismerete, másfelől a függvénytranszformációk közé bekerült a függvény abszolútértéke. Ez tehát azt jelenti, hogy az
függvény ismerete, másfelől a függvénytranszformációk közé bekerült a függvény abszolútértéke. Ez tehát azt jelenti, hogy az  függvényt (mint az
függvényt (mint az 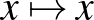 függvény abszolút értékét) továbbra is tudni kell ábrázolni (de középszinten nem kell tudni jellemezni), viszont nem kell tudni ábrázolni az
függvény abszolút értékét) továbbra is tudni kell ábrázolni (de középszinten nem kell tudni jellemezni), viszont nem kell tudni ábrázolni az 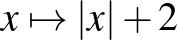 függvényt. Tehát az „alap” függvények abszolútértékét tudni kell ábrázolni, viszont az abszolútérték függvényt nem kell tudni transzformálni (középszinten). További példák olyan függvényekre, amiket a követelmények alapján tudni kell ábrázolni:
függvényt. Tehát az „alap” függvények abszolútértékét tudni kell ábrázolni, viszont az abszolútérték függvényt nem kell tudni transzformálni (középszinten). További példák olyan függvényekre, amiket a követelmények alapján tudni kell ábrázolni: 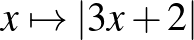 ,
, 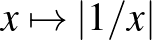 ,
, 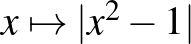 .
.
A törlesztőrészlet és a gyűjtőjáradék számolása eddig emelt szintű követelmény volt. Először két korábbi emelt szintű feladatot mutatunk, amelyek 2024-től akár középszinten is előfordulhatnának.
1. feladat (2008. októberi emelt szintű feladatsor, 9. feladat)
Egy bank a „Gondoskodás” nevű megtakarítási formáját ajánlja újszülöttek családjának. A megtakarításra vállalkozó családok a gyermek születését követő év első banki napján számlát nyithatnak 100 000 forint összeggel. Minden következő év első banki napján szintén 100 000 forintot kell befizetniük a számlára. Az utolsó befizetés annak az évnek az első banki napján történhet, amely évben a gyermekük betölti a 18. életévét. A bank év végén a számlán lévő összeg után évi 8%-os kamatot ad, amit a következő év első banki napjára ír jóvá. A gyermek a 18. születésnapját követő év első banki napján férhet hozzá a számlához.
a) Mekkora összeg van ekkor a számlán? A válaszát egész forintra kerekítse!
A gyermek a 18. születésnapját követő év első banki napján felveheti a számláján lévő teljes összeget. Ha nem veszi fel, akkor választhatja a következő lehetőséget is: Hat éven keresztül minden év első banki napján azonos összeget vehet fel. Az első részletet a 18. születésnapját követő év első banki napján veheti fel. A hatodik pénzfelvétellel a számla kiürül. Ha ezt a lehetőséget választja, akkor a bank - az első pénzfelvételtől számítva - minden év végén a számlán lévő összeg után évi 5%-os kamatot garantál, amit a következő év első banki napjára ír jóvá.
b) Ebben az esetben mekkora összeget vehet fel alkalmanként? A válaszát egész forintra kerekítse!
2. feladat (2013. május emelt szintű magyar nyelvű feladatsor, 4. feladat b) része)
Ádám is vett fel hiteleket ettől a banktól évi 8%-os kamatos kamatra. Az egyik év január 1-jén éppen 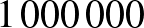 Ft tartozása volt. Több hitelt nem vett fel, és attól kezdve 10 éven keresztül minden év végén befizette az azonos összegű törlesztőrészletet. (A törlesztőrészlet összegét a bank már az éves kamattal megnövelt tartozásból vonja le.) Mekkora volt ez a törlesztőrészlet, ha Ádám a 10 befizetés után teljesen visszafizette a felvett hitelt? Válaszát ezer forintra kerekítve adja meg!
Ft tartozása volt. Több hitelt nem vett fel, és attól kezdve 10 éven keresztül minden év végén befizette az azonos összegű törlesztőrészletet. (A törlesztőrészlet összegét a bank már az éves kamattal megnövelt tartozásból vonja le.) Mekkora volt ez a törlesztőrészlet, ha Ádám a 10 befizetés után teljesen visszafizette a felvett hitelt? Válaszát ezer forintra kerekítve adja meg!
3. feladat
Kovács úr 6 év múlva autót szeretne vásárolni, ezért takarékoskodik. Minden év elején betesz a bankba egy ugyanakkora összeget. A bank 10% kamatot fizet évente. A Kovács úr által kinézett autó ára 5 000 000 Ft, amiről feltételezzük, hogy az évek során nem változik.
a) Kovács úr első számításai alapján évente 500 000 Ft-ot tud félre tenni. Mennyi pénze lesz így a bankban 6 év elteltével? Meg tudja-e vásárolni a kinézett autót?
b) Ha nem tudja megvásárolni, akkor mekkora összeget kellene félretennie évente, hogy mégis meg tudja vásárolni a kiszemelt járművet 6 év elteltével? Válaszát ezer forintra kerekítve adja meg!
c) Ha nem tud 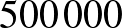 Ft-nál többet félretenni, akkor hány évig kell takarékoskodnia, hogy meg tudja venni az autót?
Ft-nál többet félretenni, akkor hány évig kell takarékoskodnia, hogy meg tudja venni az autót?
4. feladat
A Szabó család új lakást akar vásárolni. Ehhez kölcsönt vesznek fel, méghozzá 20 millió Ft-ot, 10 évre, évi 6%-os kamatra. Minden év végén törlesztik a kölcsönt és a kamatait, és 10 éven keresztül minden évben ugyanakkora összeget akarnak befizetni.
a) Mekkora lesz az éves törlesztőrészlet?
Kiderült, hogy nem tudnak ekkora összeget kifizetni évente, hanem csak 2,2 M Ft-ot.
b) Hány évig kell törleszteniük ebben az esetben a hitelt?
Most két lehetséges feladatot mutatunk a megtakarítási, befektetési és hitelfelvételi lehetőségekkel és azok kockázati tényezőivel kapcsolatban.
5. feladat
Annának van egy kis spórolt pénze, és úgy dönt, hogy befekteti. Két lehetőség közül választhat. Mindkét esetben kamatos kamatot ígér a bank, azaz a kamatot hozzászámolják a tőkéhez, és a következő alkalommal már az is kamatozik.
„Lépcső betét”: a betett pénzösszeg havonta 1,5%-kal kamatozik.
„Ugrás betét”: a befektetett pénzösszeg évente 19%-kal kamatozik.
Anna két évre szeretne lekötni 500 000 Ft-ot. Melyik lehetőség és mennyivel kedvezőbb a számára?
6. feladat
Balázs személyi kölcsönt szeretne felvenni 150 000 Ft összegben 12 hónapos futamidőre. Az alábbi két ajánlat közül választhat:
„Fix hitel”: a kölcsön kamata 15% évente, és semmilyen más díjat nem kell fizetni. A kamatot és a tőkét egy összegben, a futamidő végén kell megfizetni.
„Extra hitel”: a kölcsön kamata 10% évente, emellett a folyósítási jutalék a hitelösszeg 1,5%-a, a szerződéskötési díj pedig 9000 Ft. A folyósítási jutalékot és a szerződéskötési díjat a hitel felvételekor hozzáadják a hitelösszeghez. A kamatot és a tőkét egy összegben, a futamidő végén kell megfizetni
Melyik ajánlat kedvezőbb Balázs számára?
Egy elképzelhető emelt szintű feladat a konvexitás fogalmának alkalmazásához:
7. feladat
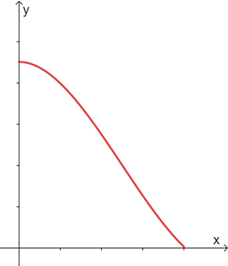
Az alábbi diagram egy vidámpark vízicsúszdájának alakját mutatja oldalnézetből. A diagram az alábbi függvénnyel közelíthető:
![$f\colon [0;4]\to \mathbf{R}$](/images/stories/latexuj/2023-09/2023-09-erettsegiiii/img40.png) ,
, 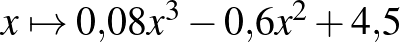 , ahol egy egység mindkét tengelyen 1 méternek felel meg. Számítsa ki, hogy milyen magasan van a csúszdának az a pontja, ahol a legmeredekebb!
, ahol egy egység mindkét tengelyen 1 méternek felel meg. Számítsa ki, hogy milyen magasan van a csúszdának az a pontja, ahol a legmeredekebb!
Csapodi Csaba
ELTE TTK Matematikatanítási és Módszertani Központ,
Rényi Alfréd Matematikai Kutatóintézet Módszertani Osztály