A cikksorozat negyedik részében közölt feladatok megoldása itt található. Az ötödik, egyben befejező részben a valószínűségszámítás és statisztika témakörének változásait ismertetjük. Először bemutatjuk az érettségi követelmények változását táblázatos formában. A táblázatban (piros színnel) jelezzük az újonnan megjelenő követelményeket és a törölt ismereteket is. (Ha egy követelmény átkerült középszintről emelt szintre, akkor azt csak a középszinten jelöljük kihúzással és emelt szinten nem pirosítottuk, hiszen eddig is része volt az emelt szintű követelményeknek.) A táblázat után a legfontosabb változásokat röviden megmagyarázzuk, értelmezzük, indokoljuk. Ezután néhány, újdonságnak számító ismeret esetén mutatunk olyan feladatokat, amelyeket a követelmények alapján el tudnánk képzelni egy feladatsorban. Hangsúlyozzuk, hogy ezek személyes elképzelések, az érettségi feladatokat összeállító bizottság nyilvánvalóan saját ötletei és szakmai meggyőződése szerint fog dolgozni.
| 5. Valószínűségszámítás és statisztika | ||
|
TÉMÁK |
VIZSGASZINTEK |
|
|
Középszint |
Emelt szint |
|
|
5.1 Leíró statisztika |
Tudjon adott adathalmazt szemléltetni. |
|
|
5.1.1 Statisztikai adatok gyűjtése, rendszerezése, különböző ábrázolásai |
Tudjon adathalmazt táblázatba rendezni és táblázattal megadott adatokat feldolgozni. Tudjon választani megfelelő diagramtípust egy adathalmaz ábrázolásához, és tudjon a választása mellett érvelni. Tudjon adott diagramról információt kiolvasni. Tudjon grafikus manipulációkat felismerni és javítani diagramok esetén. |
Tudjon adathalmazokat összehasonlítani sodrófa-diagramok alapján. |
|
5.1.2 Nagy adathalmazok jellemzői, statisztikai mutatók |
Ismerje és alkalmazza a következő fogalmakat: átlag, súlyozott számtani közép, kvartilisek, medián, módusz, terjedelem, átlagos abszolút eltérés, szórás. |
Ismerje és alkalmazza a következő fogalmakat: súlyozott számtani közép, átlagos abszolút eltérés. Tudjon választani az adathalmazt jól jellemző középértéket, és tudjon a választása mellett érvelni. Tudjon statisztikai adatokat értelmezni, értékelni, azokból tudjon statisztikai következtetéseket levonni. |
|
5.2 A valószínűségszámítás elemei |
Ismerje és alkalmazza konkrét példák esetén a következő fogalmakat: esemény, eseménytér, elemi esemény, események összege és szorzata, esemény komplementere, egymást kizáró események, független események. Ismerje és alkalmazza a geometriai valószínűség modelljét. |
Definiálja és alkalmazza a középszinten felsorolt fogalmakat. Definiálja és alkalmazza a feltételes valószínűség fogalmát. |
|
Tudjon valószínűséget számítani visszatevéses és visszatevés nélküli mintavétel esetén. Tudja meghatározni a várható értéket konkrét feladatokban. |
Tudja értelmezni a binomiális eloszlást (visszatevéses modell) és a hipergeometriai eloszlást (visszatevés nélküli modell). Tudjon ezek alkalmazásával konkrét valószínűségeket kiszámítani. |
|
Látható, hogy ebben a témakörben sok változás történt: új ismeretek, elvárások kerültek be mind a közép-, mind az emelt szintű követelmények közé. (Ennek megítélésével nem szeretnénk túl sokat foglalkozni, de azt megemlítjük, hogy egyfelől nem túl nehezek az új fogalmak, másfelől ezek tanulása elengedhetetlennek tűnik ahhoz, hogy megfelelően el tudjunk igazodni a ránk zúduló adathalmazok, a sokszor manipulatív diagramok között. Azt sem felejthetjük el, hogy a pandémia alatt milyen fontos döntéseket kellett meghoznunk tesztek megbízhatóságát vagy oltások hatékonyságát ismerve.)
A sok változás között az egyetlen igazi újdonságot a kvartilisek fogalmának és a sodrófa (másnéven box-plot vagy doboz-) diagram ismeretének követelménye jelenti. Ezért ezekkel az alábbiakban egy kicsit részletesebben foglalkozunk. Előrebocsátjuk, hogy a kvartilisek ismerete arra ad lehetőséget, hogy az adathalmazokat néhány számadattal jobban tudjuk jellemezni, mint kizárólag középértékekkel (átlag, medián). Fontos azt is tudni, hogy a kvartilisek elsősorban nagy adathalmazok jellemzésére használhatók és használandók, de nyilvánvaló, hogy a jelenlegi érettségi viszonyok között nincs lehetőség ilyenek elemzésére.
A kvartilisek azok a helyzetmutatók, amelyek a nagyság szerint növekvő sorba rendezett adatokat négy, lehetőleg egyenlő nagyságú részre osztják.
- Az alsó kvartilis az a szám, amelynél az adatok (körülbelül) 25%-a kisebb (jele: Q1, használjuk az első kvartilis megnevezést is);
- a medián (Q2 = Me, a második kvartilis);
- a felső kvartilis az a szám, amelynél az adatok (körülbelül) 75%-a kisebb (jele: Q3, a harmadik kvartilis).
A kvartilisek meghatározása
A kvartilisek meghatározásának diszkrét eloszlások esetén nincs általánosan elfogadott módszere. A 2020-as Nat-nak megfelelően átdolgozott tankönyvek a következő módszerrel dolgoznak, így ezt javasoljuk a diákoknak az érettségi vizsgán is:
- A nagyság szerint növekvő sorba rendezett adatokat a mediánnál két részre osztjuk.
- Ha páratlan számú adattal dolgozunk, akkor a mediánt (tehát a sorbarendezett adatok középső elemét) elhagyjuk az adatok közül. Ha páros számú adattal dolgozunk, akkor egyszerűen középen kettéválasztjuk az adatokat.
- Az alsó kvartilis az eredeti adathalmaz „alsó felének”, a felső kvartilis pedig a „felső felének” a mediánja.
Felhívjuk a figyelmet arra, hogy a leggyakrabban használt számítógépes programok közül a GeoGebra ugyanezzel a módszerrel számol, viszont a legtöbb táblázatkezelő program (köztük az MS Excel) eltérő módszerrel dolgozik, ami bizonyos elemszámok esetén a fentiektől eltérő eredményt ad.
A kvartilis értékek az első 8, 9, 10, illetve 11 pozitív számból álló adatsokaság esetén:
|
Adatok |
Kvartilisek |
||
|
Q1 |
Q2 |
Q3 |
|
|
1-8 |
2,5 |
4,5 |
6,5 |
|
1-9 |
2,5 |
5 |
7,5 |
|
1-10 |
3 |
5,5 |
8 |
|
1-11 |
3 |
6 |
9 |
A statisztikában kiugró adatnak (outlier) azt az adatot nevezzük, amelyik jelentősen eltér a többi adattól. Ilyen adat keletkezhet pl. egy mérés nagy szórása esetén, de jelezhet mérési hibát is. Általános definíció nincs arra nézve, hogy mit értünk „jelentős” eltérés alatt. Egy gyakran használt megközelítés szerint azok az adatok tekinthetők kiugrónak, amelyek eltérése a felső (alsó) kvartilistól a félterjedelem 1,5-szeresénél nagyobb „felfelé” („lefelé”). Miután az érettségi követelmények nem tesznek említést a kiugró adat ismeretéről, ezért nem várható olyan feladat a vizsgán, ami ennek ismeretét kérné számon.
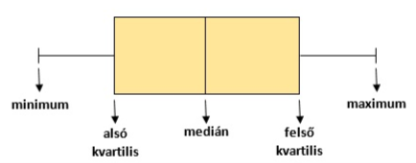
A sodrófa- vagy dobozdiagram (box-plot)
Ez a diagram alapvetően a fent említett öt érték vizuális megjelenítésére szolgál. A doboz széleit az alsó és felső kvartilis adja, a dobozban megjelenik a medián is. A dobozból induló szakaszok vége az adatok minimumát és maximumát jelzi. A diagram lehet fekvő és álló is.
1. feladat
Kördiagrammal vagy oszlopdiagrammal ábrázolná inkább az alábbi adatokat? Válaszát indokolja!
a) Egy iskola tanulói létszámának alakulása 2020 és 2024 között.
b) Az osztály tanulóinak megoszlása a szülők legmagasabb iskolai végzettsége szerint.
c) Egy osztályban a matematika érettségi jegyek eloszlása.
2. feladat
Ádám egy év júliusában feljegyzi mind a 31 napon a lakóhelyén mért legmagasabb napi hőmérsékletet (Celsius fokban), majd az adatokat nagyság szerint sorbarendezi. Így ezt az adatsokaságot kapja:
19, 22, 22, 23, 23, 23, 25, 26, 26, 26, 26, 27, 27, 27, 27, 27, 28, 28, 29, 31, 31, 32, 32, 33, 33, 35, 38, 39, 40, 40, 42
Ábrázolja az adatokat sodrófa-diagramon!
3. feladat
Egy 24 fős osztályba 12 fiú és 12 lány jár. Egy próbaérettségi dolgozat eredményei a fiúk között: 32, 38, 40, 52, 53, 54, 56, 60, 61, 64, 66, 84.
a) Sorolja az adatokat osztályokba, és ábrázolja ennek alapján a fiúk eredményét oszlopdiagrammal!
A lányok eredményei ugyanennél a dolgozatnál: 37, 38, 44, 53, 54, 57, 59, 60, 61, 62, 63, 65. Timi szerint a lányok eredményei jobbak, mint a fiúk eredményei. Gergő szerint pont fordítva: a fiúk értek el jobb eredményt, mint a lányok.
b) Mondjon egy érvet, ami Timi, és egy másikat, ami Gergő álláspontját támasztja alá!
Az évfolyam egy másik osztályában ugyanezen dolgozaton elért eredményekről az alábbi diagram készült.

c) Hasonlítsa össze a két osztály eredményét az adatok terjedelme és mediánja alapján!
4. feladat
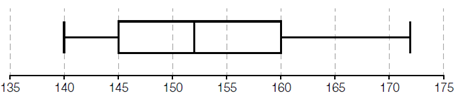
Az alábbi sodrófadiagramok egy iskola két párhuzamos osztályába járó diákok centiméterben mért magasságának eloszlását mutatják. A két osztályba ugyanannyi diák jár.
|
A osztály |
 |
|
B osztály |
 |
Az alábbi kijelentések a fenti adatokra vonatkoznak. Állapítsa meg minden kijelentésről, hogy igaz, hamis, vagy az adatok alapján ezt nem lehet eldönteni! (Tegyen X-et a megfelelő cellába! Válaszait nem kell indokolnia.)
|
Igaz |
Hamis |
Nem lehet eldönteni |
|
|
Az A osztályba járó gyerekek több mint fele alacsonyabb 150 cm-nél. |
|||
|
A B osztályban több olyan gyerek van, aki 160 cm-nél magasabb, mint az A osztályban. |
|||
|
A magasságok terjedelme az A osztályban nagyobb, mint a B osztályban. |
|||
|
A két osztály összes tanulója közül a legmagasabb az A osztályba jár. |
5. feladat
Egy kisváros fürdőjét 2024 nyarán szeretné felújítani a helyi önkormányzat. Az alábbi táblázat tartalmazza, hogy az elmúlt 8 évben hogyan alakult a fürdő látogatottsága éves szinten:
|
Év |
2016 |
2017 |
2018 |
2019 |
2020 |
2021 |
2022 |
2023 |
|
Fürdővendégek száma |
33 200 |
32 500 |
34 000 |
33 500 |
33 200 |
33 100 |
32 900 |
32 500 |
A beruházást ellenző egyik képviselő az alábbi grafikont hozza nyilvánosságra közösségi oldalán:
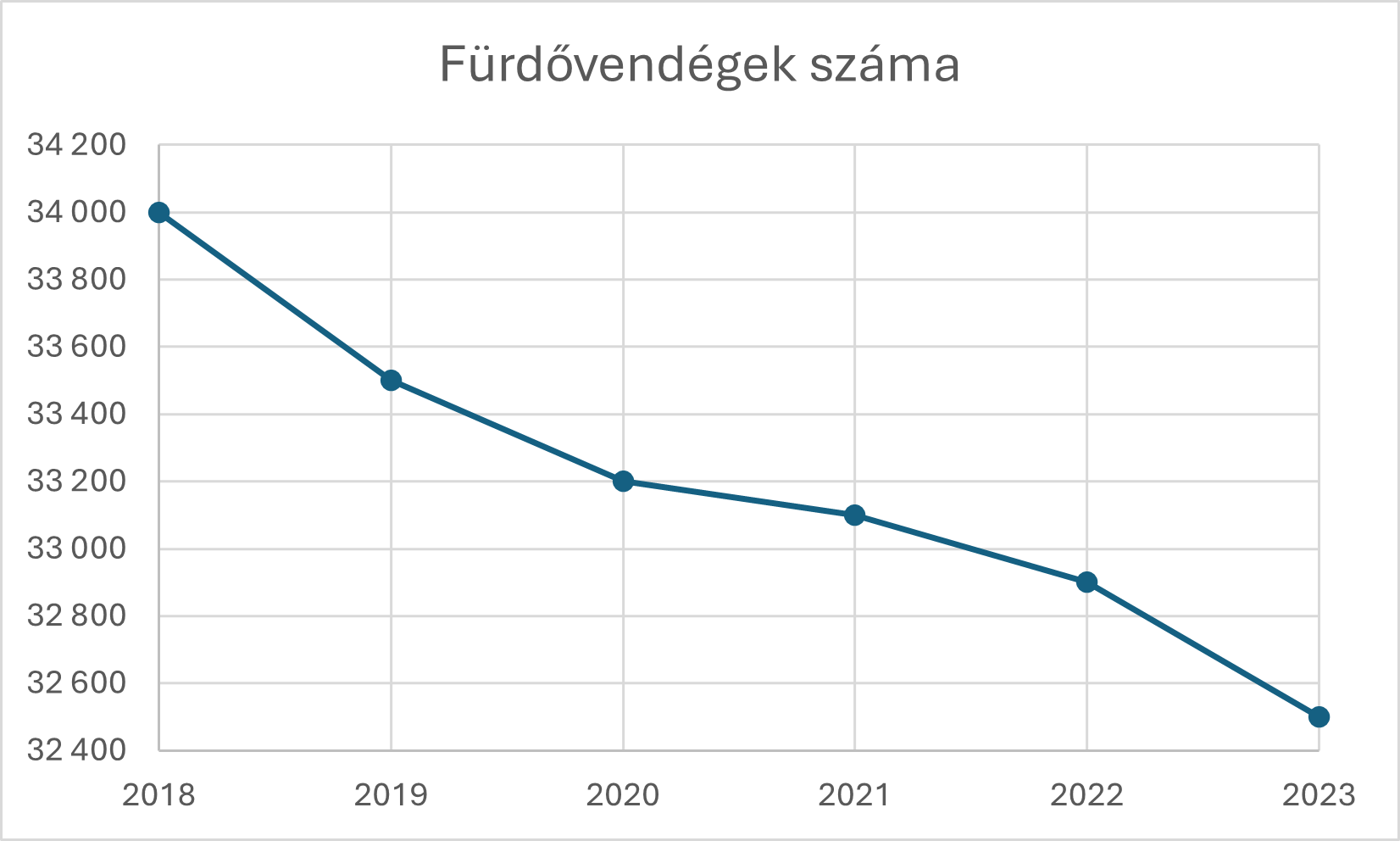
a) Írjon két olyan jellemzőt, amiért ez a grafikon téves következtetések levonására alkalmas!
b) Ábrázolja az adatokat úgy, hogy nehezebben lehessen belőlük téves következtetéseket levonni!
6. feladat
András az első félévben négy jegyet kapott matematikából. Tanára szerint a jegyei alapján félévkor 4-est érdemel, mert ez a jegyek átlaga. András szerint viszont 5-öst kéne kapnia, mert ez a jegyeinek az egyetlen módusza, és 4-es jegye nem is volt a félév során. Milyen jegyeket kapott András a félév során? Válaszát indokolja!
7. feladat
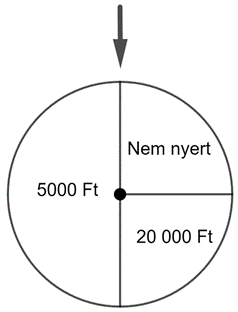
Egy új bevásárlóközpontban nyitási akcióként minden vásárló megpörgetheti az ábrán látható szerencsekereket. Amelyik mezőnél a kerék megáll a pörgetés után, azt az összeget nyeri meg a vásárló. Mennyi a nyeremény várható értéke egy pörgetés esetén? Megoldását részletezze!
Csapodi Csaba
Eötvös Loránd Tudományegyetem Tanárképző Központ,
ELTE TTK Matematikatanítási és Módszertani Központ











