A cikksorozat harmadik részében közölt feladatok megoldása itt található. A negyedik részben a geometria témakörének változásait mutatjuk be. Először az érettségi követelmények változását ismertetjük táblázatos formában. A táblázatban (piros színnel) jelezzük az újonnan megjelenő követelményeket és a törölt ismereteket is. (Ha egy követelmény átkerült középszintről emelt szintre, akkor azt csak a középszinten jelöltük kihúzással és emelt szinten nem pirosítottuk ki, hiszen eddig is része volt az emelt szintű követelményeknek.) A táblázat után a legfontosabb változásokat röviden megmagyarázzuk, értelmezzük, indokoljuk. Ezután néhány, újdonságnak számító ismeret esetén mutatunk olyan feladatokat, amelyeket a követelmények alapján el tudnánk képzelni egy feladatsorban. Hangsúlyozzuk, hogy ezek személyes elképzelések, az érettségi feladatokat összeállító bizottság nyilvánvalóan saját ötletei és szakmai meggyőződése szerint fog dolgozni.
4. Geometria |
||
|
TÉMÁK |
VIZSGASZINTEK |
|
|
Középszint |
Emelt szint |
|
|
4.1 Elemi geometria |
Ismerje és használja megfelelően az alapfogalom, axióma, definiált fogalom, bizonyított tétel fogalmát. |
|
|
4.1.1 Térelemek 4.1.2 A távolságfogalom segítségével definiált ponthalmazok |
Ismerje a térelemeket és a szög fogalmát. |
|
|
4.2 Geometriai transzformációk |
Ismerje a geometriai transzformációk és a függvények kapcsolatát. |
|
|
4.2.1 Egybevágósági transzformációk |
Ismerje a síkbeli egybevágósági transzformációk (eltolás, tengelyes tükrözés, középpontos tükrözés, pont körüli forgatás) leírását, tulajdonságaikat, és alkalmazza ezeket feladatokban. |
Tudja pontosan megfogalmazni az egybevágósági transzformációk definícióit, a síkidomok egybevágóságának fogalmát, valamint a sokszögek egybevágóságának feltételét. |
|
4.2.2 Hasonlósági transzformációk |
Ismerje a középpontos hasonlósági transzformáció leírását, tulajdonságait. |
Ismerje a középpontos hasonlósági transzformáció és a hasonlósági transzformáció definícióját. |
|
4.2.3 Egyéb transzformációk |
||
|
Merőleges vetítés |
Ismerje és alkalmazza feladatokban a merőleges vetítést. |
|
|
4.3 Síkbeli és térbeli alakzatok |
Ismerje a síkidomok, testek csoportosítását különböző szempontok szerint. |
|
|
4.3.1 Síkbeli alakzatok |
||
|
Háromszögek |
Tudja csoportosítani a háromszögeket oldalak és szögek szerint. |
|
|
Ismerje és alkalmazza a háromszög nevezetes vonalaira, pontjaira és köreire vonatkozó definíciókat, tételeket (oldalfelező merőleges, szögfelező, magasságvonal, magasságpont, súlyvonal, súlypont, középvonal, körülírt, illetve beírt kör). Bizonyítsa az oldalfelező merőlegesek és a belső szögfelezők metszéspontjára vonatkozó tételt. |
Bizonyítsa a háromszög nevezetes vonalaira, pontjaira és köreire vonatkozó tételeket. |
|
|
Ismerje és alkalmazza a Pitagorasz-tételt és megfordítását. Bizonyítsa a Pitagorasz-tételt. Ismerje és alkalmazza a magasság- és a befogótételt. |
Bizonyítsa a Pitagorasz-tétel megfordítását. |
|
|
Négyszögek |
Ismerje a speciális négyszögek fajtáit (trapéz, paralelogramma, deltoid, rombusz, téglalap, négyzet) és tulajdonságaikat, ismereteit alkalmazza egyszerű feladatokban. |
Bizonyítsa a húrnégyszögek és az érintőnégyszögek tételét, ismerje a tételek megfordítását. Ismereteit alkalmazza feladatok megoldásában. |
|
Sokszögek |
Ismerje, bizonyítsa és alkalmazza konvex sokszögeknél az átlók számára, a belső és külső szögösszegre vonatkozó tételeket. Ismerje a szabályos sokszögek definícióját. |
|
|
Kör |
Ismerje a kör részeit, ismereteit alkalmazza egyszerű feladatokban. |
Bizonyítsa, hogy a kör érintője merőleges az érintési pontba húzott sugárra, valamint hogy a külső pontból húzott érintőszakaszok egyenlő hosszúak. |
|
Ismerje és alkalmazza feladatokban a Thalész-tételt és megfordítását. Bizonyítsa a Thalész-tételt. |
Bizonyítsa a Thalész-tétel megfordítását. |
|
|
4.3.2 Térbeli alakzatok |
Ismerje a következő testeket és azok részeit, alkotóelemeit: hasáb, henger, gúla, kúp, gömb, csonkagúla, csonkakúp. Ismereteit alkalmazza egyszerű feladatokban. |
|
|
4.4 Vektorok síkban és térben |
Ismerje és alkalmazza feladatokban a következő definíciókat, tételeket: |
Ismerje és alkalmazza a vektorműveletekre vonatkozó műveleti azonosságokat. Ismerje és alkalmazza a skaláris szorzat definícióját, tulajdonságait. |
|
Ismerje és alkalmazza feladatokban a következő definíciókat, tételeket: |
Tudja koordinátáikkal adott vektorok hajlásszögét meghatározni. |
|
|
4.5 Trigonometria |
Tudja hegyesszögek szögfüggvényeit derékszögű háromszög oldalarányaival definiálni, ismereteit alkalmazza feladatokban. Tudja a szögfüggvények általános definícióját. . |
Ismerje a szögfüggvények általános definícióját, és alkalmazza forgásszögekre a középszinten szereplő összefüggéseket. |
|
Ismerje és alkalmazza a nevezetes szögek (30°, 45°, 60°) szögfüggvényeit. Bizonyítsa a szinusztételt. |
Függvénytáblázat segítségével tudja alkalmazni egyszerű feladatokban az addíciós összefüggéseket (sin(α + β) , cos(α + β), tg(α + β), sin 2α, cos 2α, tg 2α). |
|
|
4.6 Koordinátageometria |
Tudja kiszámítani |
|
|
4.6.1 Pontok, vektorok |
Tudja kiszámítani két pont távolságát. |
Igazolja a szakasz felezőpontja és harmadoló pontjai koordinátáinak kiszámítására vonatkozó összefüggéseket. |
|
4.6.2 Egyenes |
Tudja felírni különböző adatokkal meghatározott egyenesek egyenletét y = mx + b illetve x = c alakban. |
Tudja többféle alakban felírni és levezetni az egyenes egyenletét a síkban különböző kiindulási adatokból. Ismerje egyenesek párhuzamosságának és merőlegességének koordinátageometriai feltételeit. |
|
4.6.3 Kör |
Tudja felírni adott középpontú és sugarú kör egyenletét. |
Tudja levezetni a kör egyenletét. Tudja meghatározni kétismeretlenes másodfokú egyenletből a kör középpontját és sugarát. |
|
4.6.4 Parabola |
Tudja levezetni a parabola x2 = 2py alakú egyenletét. |
|
|
4.7 Kerület, terület |
Ismerje a kerület és a terület szemléletes fogalmát. |
Bizonyítsa a háromszög területének kiszámítására használt képleteket, továbbá ismerje és alkalmazza az alábbi összefüggéseket: |
|
|
||
|
Tudja kiszámítani nevezetes négyszögek, szabályos sokszögek, továbbá kör, körcikk, körszelet, körgyűrű kerületét és területét. |
Bizonyítsa nevezetes négyszögek és szabályos sokszögek területképleteit. |
|
|
4.8 Felszín, térfogat |
Ismerje a felszín és a térfogat szemléletes fogalmát. |
Bizonyítsa a csonkagúla és a csonkakúp térfogatképletét. |
Mint látható, sok változás történt ebben a témakörben, de a változások nagy része – mindkét szinten – abból áll, hogy a korábban a követelmények részét képző ismeret kikerült a RÉV-ből.
Középszintről kikerült (de továbbra is az emelt szintű követelmények részét képezi) a magasság- és befogótétel ismerete, az ívmérték, a skaláris szorzat fogalma, a valós számok halmazán értelmezett trigonometria. Jelentős változás, hogy ezentúl az egyenesnek csak a meredekséggel felírható alakját kell tudni alkalmazni, nem kell ismerni a normál- és irányvektor fogalmát. Sokat egyszerűsödtek a körre vonatkozó koordinátageometriai ismeretek is (nyilvánvalóan azzal összefüggésben, hogy nem kell tudnia a vizsgázóknak másodfokú egyenletrendszert megoldani). Középszinten bekerült több tétel bizonyításának ismerete a követelmények közé. (Itt emlékeztetünk arra, amit az I. részben már leírtunk: ez nem jelenti azt, hogy a középszintű matematika írásbeli vizsgán a diákoknak valamely, a követelményekben szereplő tétel bizonyítását kellene leírniuk. Ha valahol ezek a bizonyítások megjelenhetnek, az a szóbeli vizsga, erre a 2024-től érvényes vizsgaleírás is utal.)
Emelt szintről is kikerült néhány ismeret követelménye.
Miután ezt a témakört inkább a követelmények csökkenése jellemzi, így kevés igazi újdonságot jelentő mintafeladatot tudunk mutatni. A korábbi évek feladatsorainak azok a feladatai, amelyek megfelelnek a követelményeknek, továbbra is jól használhatók az érettségi vizsgára történő felkészítés során.
- Egy egyenlőszárú háromszög egyik szögéről tudjuk, hogy szinusza
 , koszinusza pedig
, koszinusza pedig 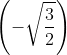 . Mekkorák a háromszög szögei?
. Mekkorák a háromszög szögei? - Flóra szerint, ha két háromszögről tudjuk, hogy szögeik megegyeznek, és van egy-egy egyenlő hosszúságú oldaluk, akkor a két háromszög egybevágó. Igaza van-e Flórának? Válaszát indokolja!
- Egy háromszögről tudjuk, hogy két magassága egyenlő hosszú. Bizonyítsa be, hogy a háromszög egyenlőszárú!
- Egy paralelogramma egyik átlója szögfelező egyben. Mutassa meg, hogy ez a paralelogramma egy rombusz!
- Írja fel annak az egyenesnek az egyenletét, amely illeszkedik az A (–1; 5) és B (8; –13) pontokra!
Végül a 18. feladat a 2023. őszi középszintű feladatsorból megmutatja, hogy a körgyűrű területének kiszámítása tulajdonképpen eddig is részét képezte a követelményeknek.
 Egy párnákat gyártó cég a képen látható ülőpárnát szivacsból készíti, majd szövettel befedi. A szivacsból először egy 42 cm átmérőjű, 7 cm magasságú körhengert vágnak ki. Ezután a henger közepéből kivágnak egy 18 cm átmérőjű kisebb körhengert. (A két henger alapkörének középpontja egybeesik.)
Egy párnákat gyártó cég a képen látható ülőpárnát szivacsból készíti, majd szövettel befedi. A szivacsból először egy 42 cm átmérőjű, 7 cm magasságú körhengert vágnak ki. Ezután a henger közepéből kivágnak egy 18 cm átmérőjű kisebb körhengert. (A két henger alapkörének középpontja egybeesik.)
a) Számítsa ki a párna szivacsos részének térfogatát!
b) Mennyi szövetre van szükség 30 párna befedéséhez? Válaszát négyzetméterben, egészre kerekítve adja meg! (A veszteségektől itt eltekintünk.)
Csapodi Csaba
ELTE TTK Matematikatanítási és Módszertani Központ,
Rényi Alfréd Matematikai Kutatóintézet Módszertani Osztály












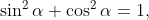
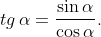
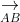 vektor koordinátáit, abszolútértékét.
vektor koordinátáit, abszolútértékét.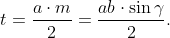
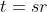 (bizonyítással),
(bizonyítással), 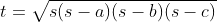 .
.