Marguerite, a számok szerelmese

A cím egy érdekes játékfilmre utal, amelynek főhősnője a Szemerédi-tételből kiindulva bebizonyítja a Goldbach-sejtést (a következtetés nem igaz). A Wikipédia segítségével elolvasható a film leírása, a Goldbach-sejtés és a Szemerédi-tétel, mégsem tartom feleslegesnek a három kérdést egy rövid cikkben tárgyalni. Egyébként az Érintő egy korábbi cikke [Titkos (2021)] a Szemerédi-tétel történetét részletesen bemutatta.

A filmről

Hiszek abban, hogy egy jó játékfilm is szólhat komoly dolgokról, mint amilyen például a matematika. A múltból két olyan játékfilmre emlékszem, amely matematikusokról szólt: a Good Will Hunting (1997) és az Egy csodálatos elme (2001). Az első nem kapcsolódott konkrét témához, és mégis kiemelkedőnek tartom; a másik John Nash-ről szólt, aki 1994-ben közgazdasági Nobel-díjat kapott (és a film elkészítése után, 2015-ben matematikai Abel-díjjal tüntették ki), és mégsem tartottam művészileg hitelesnek.

A jelen filmben szereplő matematikusnő nem létezett, és a Goldbach-sejtés már 1742 óta ellenáll a bizonyítási kísérleteknek, és a Szemerédi-tételnek kevés köze van a Goldbach-sejtéshez. A filmet mégis jónak tartom, mert lélektanilag hitelesen mutatja be, milyen lehet egy PhD-jén dolgozó matematikusnő élete: nehéz matematikai feladatot kell megoldania, hogy figyelmet kapjon; de fenyegeti a veszély, hogy nem sikerül a feladatot megoldania. A film elején is az utóbbi esettel találkozunk: egy PhD-s fiútársa megmutatja, hogy a lány bizonyítása nem jó.

Ezért a lány otthagyja a doktori programot, megpróbál szakképzetlen munkákból megélni, végül is kiváló számolóképességét kamatoztatva, illegális szerencsejátékból él. Aztán előkerül a fiú, segít a lánynak a bizonyítást kijavítani, és végül a lány egyedül bizonyítja be a Goldbach-sejtést.

Bár lehet, hogy matematikatörténetet tanító matematikus-közgazdászként elfogult vagyok, remélem, hogy másoknak is tetszik a film. Talán nem felesleges, ha a cikk hátralévő részében röviden ismertetem a két matematikai témát.

A Goldbach-sejtés

A Goldbach-sejtésről kiváló áttekintést nyújt Pintz János előadása [Pintz (2004/2014)]. A sejtést Euler tette nevezetessé:

Goldbach-sejtés. Minden 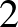-nél nagyobb páros szám felírható 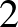prímszám összegeként.

Például 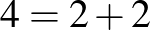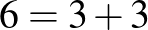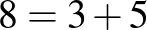$4=2+2$ , $6=3+3$ , $8=3+5$ stb. Nagyon egyszerű megérteni, nagyon nehéz lesz bebizonyítani.

Goldbach eredetileg egy könnyebb sejtést fogalmazott meg: minden 6-nál nagyobb páratlan szám fölírható legfeljebb 3 prímszám összegeként. (Valóban, az Euler-alakban szereplő felbontáshoz hozzáadva 3-at, adódik a gyengébb sejtés, de fordítva nem.) Jellemző, hogy a matematikusok egész sora megpróbált a sejtésnél egyszerűbb tételt igazolni. Például Rényi Alfréd a következő tételt igazolta:

1. tétel. (Rényi, 1948). Minden 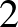-nél nagyobb páros szám felírható egy prímszám és egy olyan szám összegeként, amelynek legfeljebb 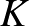prímtényezője van, ahol 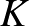elegendően nagy természetes szám.

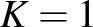Megjegyzés. Chen (1973) igazolta, hogy $K\le 2$ . A sejtés bizonyítását $K=1$ adná.

A Szemerédi-tétel

Bonyolultabb a Szemerédi-tétel. Kimondásához szükség lesz egy előzetes tételre, egy sejtésre és egy definícióra.

2. tétel (van der Waerden, 1928). Ha az egész számokat két diszjunkt részhalmazra bontjuk, akkor legalább az egyikük tartalmaz tetszőleges hosszúságú számtani sorozatot.

Megjegyzés. Az egész számokat két diszjunkt részhalmazra oszthatjuk úgy, hogy egyik sem tartalmaz végtelen hosszúságú számtani sorozatot. Képletben: adott 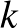$k$ természetes számra a kijelölt részhalmazba tartozó 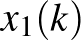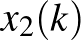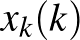$x_1(k)$ , $x_2(k)$ , …, $x_k(k)$ folytatása, 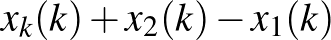$x_k(k)+x_2(k)-x_1(k)$ nem tartozik a kijelölt részhalmazba.

Fölvetődik a természetes kérdés: mit kell föltenni az egész számok egy részhalmazáról, hogy tartalmazzon tetszőlegesen hosszú számtani sorozatot?

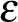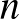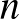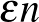Definíció. Egész számok részhalmazát pozitív felső sűrűségűnek nevezzük, ha létezik olyan pozitív valós $\varepsilon$ szám, hogy végtelen sok $n$ -re teljesül, hogy az $n$ -nél kisebb elemek száma legalább $\varepsilon n$ .

Például a páratlan számok felső sűrűsége 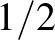$1/2$ , a prímszámoké 0. A kérdésre vonatkozik a következő

Sejtés (Erdős–Turán, 1936). Az egész számok minden pozitív felső sűrűségű részhalmazában létezik tetszőleges hosszúságú számtani sorozat.

Szemerédi tétele igazolta a nevezett sejtést.

3. tétel (Szemerédi, 1975). Az egész számok minden pozitív felső sűrűségű részhalmazában tetszőleges hosszúságú számtani sorozat létezik.

A bizonyítás eléggé hosszú, és az úgynevezett regularitási lemmán alapul, amely talán még az eredeti tételnél is fontosabb, ezt azonban már nem részletezzük. (vö. Titkos, 2021)

Érdekes, hogy erre a tételre hamarosan többféle bizonyítás született, és az egyiket a következő irányban fejlesztették tovább.

4. tétel (Green–Tao, 2008). A prímszámok halmazában is létezik tetszőleges hosszúságú számtani sorozat.

Megjegyzések.

1. Bár a bizonyításban fölhasználták a Szemerédi-tételt, messze túlléptek az eredeti érvényességi körön, hiszen a prímszámok 0 sűrűségű részhalmaz.

2. A konkrét számszerű válasz nehézséget jól érzékelteti az a Wikipédiáról letölthető információ, hogy 2019-ben a leghosszabb ilyen számtani sorozat 27 tagú volt és az induló tagja 18 jegyű volt.

Irodalomjegyzék

: Chen, J. R. (1973): On the representation of a larger even integer as the sum of a prime and the product of at most two primes. Sci. Sinica. 16: 157–176.

Erdős, P.–Turán, P. (1936): On some sequences of integers, J. of London Math Soc., 11, 261–264.

Green, B.–Tao, T. (2008): The primes contain arbitrary long arithmetic progressions, Annals of Mathematica, 167:2, 481–541.

Pintz, J. (2004/2014): A Goldbach sejtésről, Budapest, MTA.

Rényi, A. A. (1948): Egy páros szám előállításáról mint egy prím és egy majdnem prím összege. Izvestiya Akademii Nauk SSSR Seriya Matematicheskaya (oroszul). 12: 57–78.

Szemerédi, E. (1975): On sets of integers containing no 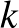$k$ elements of arithmetic progression, Acta Arithmetica, 27:1, 199–245.

Titkos, T (2021): Mi is...a regularitási lemma? https://ematlap.hu/tudomany-tortenet-2021-7/1098-a-regularitasi-lemma

van der Waerden, B. L. (1928): Beweis einer Baudetchen Vermutung, Niew. Arch. Wiks. 15, 212–216.

Simonovits András

Szemerédi Endre interjúja a filmmel kapcsolatban:

Nemrég jelent meg a fenti film apropóján egy interjú a Magyar Hírlapban az Ábel-díjas matematikussal, aki hallott a filmről, még nem látta, őt a filmesek nem keresték meg. Akit a témának ez a háttere is érdekel, kattintson ide: https://www.magyarhirlap.hu/kultura/20240526-a-szemeredi-tetel-egy-francia-filmben#google_vignette (2024. jún 10-én elérhető).