Az Abel-díj 2012-es átadása óta rengeteget (pontosabban: még a korábbinál is többet) hallani Szemerédi Endre regularitási lemmájáról és annak fontosságáról. Mára a regularitási lemmának megszámlálhatatlanul sok verziója létezik, fogalmazhatunk úgy is, hogy egy egész elmélet nőtt ki belőle.

1. ábra. Szemerédi Endre az Abel-díjjal
Magáról a lemmáról beszélve Szemerédi Endre mindig megjegyzi, hogy ugyan az alapokat ő tette le, feltétlenül meg kell említeni azokat a kiváló matematikusokat, akik aztán a munkáját továbbfejlesztették. Ezt alátámasztandó megemlítünk néhány kiemelkedő eredményt (a teljesség igénye nélkül): Timothy Gowers 2007-ben analóg állítást bizonyított hipergráfokra [3], Terence Tao megadta a lemma egy valószínűségelméleti és információelméleti megközelítését [8], Lovász László és Szegedy Balázs pedig a gráfelmélet és az analízis területeit összekapcsolva megteremtette a regularitási lemma különböző analitikus alakjait. [5].
Ennek a cikknek az apropóját Lovász László Abel-díja és az imént említett kapcsolat szolgáltatja. A Szemerédi's Lemma for the Analyst című cikk nem csak Szemerédi Endre szerény állítását segít alátámasztani (értsd: nagy matematikusok vitték tovább, amit ő elkezdett), hanem jól példázza azt a gyakran emlegetett tényt is, hogy Lovász László eredményei a matematika különböző, egymástól távol eső területei között építenek hidat. (A tiszteletére szervezett konferenciák és a Bolyai Társulat gondozásában megjelenő ünnepi kötetek nem véletlenül kapták a „Building Bridges” címet.)


2. ábra. A Building Bridges kötetek borítói I,II
1. Az Erdős–Turán sejtés
Mielőtt a regularitási lemmára térnénk, feltétlenül szót kell ejtenünk az Erdős-Turán sejtésről.

3. ábra. Erdős Pál és Turán Pál
Nem sok olyan fogalom van a matematikában, amiről bizton állíthatjuk, hogy mindenki találkozott vele. Ám az egyik ilyen a számtani sorozat fogalma: egész számok egy 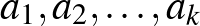 sorozatát
sorozatát 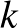 hosszúságú számtani sorozatnak nevezzük, ha a szomszédos tagjainak eltérése állandó, azaz ha van olyan
hosszúságú számtani sorozatnak nevezzük, ha a szomszédos tagjainak eltérése állandó, azaz ha van olyan 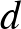 szám, amelyre
szám, amelyre 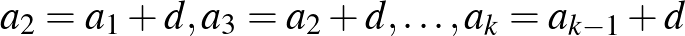 . Így például a 13, 20, 27, 34, 41, 48 egy 6 hosszúságú számtani sorozat, amelynek első tagja
. Így például a 13, 20, 27, 34, 41, 48 egy 6 hosszúságú számtani sorozat, amelynek első tagja 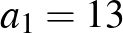 , differenciája pedig
, differenciája pedig 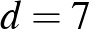 . Ahhoz, hogy az Erdős-Turán sejtéshez egy lépéssel közelebb kerüljünk, képzeljük el a következő játékot.
. Ahhoz, hogy az Erdős-Turán sejtéshez egy lépéssel közelebb kerüljünk, képzeljük el a következő játékot.
Adnak nekünk egy hatalmas 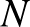 , és egy kicsi
, és egy kicsi 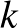 számot, a példa kedvéért legyen
számot, a példa kedvéért legyen 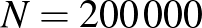 és
és 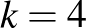 . A feladatunk az, hogy az 1, 2, 3, ...,
. A feladatunk az, hogy az 1, 2, 3, ..., 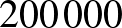 egész számok közül kiválasszuk a lehető legtöbbet úgy, hogy a kiválasztott számhalmaz ne tartalmazzon
egész számok közül kiválasszuk a lehető legtöbbet úgy, hogy a kiválasztott számhalmaz ne tartalmazzon 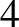 hosszúságú számtani sorozatot. Ha például a már kiválasztott számaink között szerepel a
hosszúságú számtani sorozatot. Ha például a már kiválasztott számaink között szerepel a 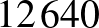 , a
, a 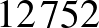 , és a
, és a 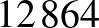 , akkor nem választhatjuk ki sem a
, akkor nem választhatjuk ki sem a 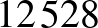 -at, sem a
-at, sem a 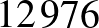 -ot, mert ezek bármelyikével létrejönne egy
-ot, mert ezek bármelyikével létrejönne egy 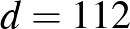 differenciájú
differenciájú 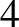 tagú számtani sorozat.
tagú számtani sorozat.
Világos, hogy a feladatunk lépésről lépésre nehezebb lesz, hiszen minél több kiválasztott számunk van, annál több lesz a fentihez hasonló megkötés. Az is világos, hogy bármilyen stratégia szerint is válogatunk, előbb-utóbb meg kell állnunk. (Annál is inkább, mert összesen 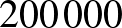 számunk van, tehát a játéknak legfeljebb
számunk van, tehát a játéknak legfeljebb 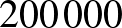 lépése lehet.) A meglepő az, hogy a valóság ettől a
lépése lehet.) A meglepő az, hogy a valóság ettől a 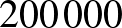 -től nagyon távol van: bármilyen stratégiát is választunk, a számoknak csak egy kis töredékét tudjuk kiválasztani. Hogy pontosan mennyire kicsi ez a töredék, abba nem megyünk bele, de
-től nagyon távol van: bármilyen stratégiát is választunk, a számoknak csak egy kis töredékét tudjuk kiválasztani. Hogy pontosan mennyire kicsi ez a töredék, abba nem megyünk bele, de 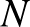 méretéhez képest elenyésző.
méretéhez képest elenyésző.
Egy pillanatra gondolkodjunk most el azon, hogy milyen stratégiát követnénk, ha nem csak az 1, 2, 3, ..., 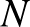 számok közül, hanem az összes pozitív egész számból válogathatnánk. Az az ember érzése, hogy egyre nagyobb és nagyobb számokat kéne választani, egyre nagyobb réseket hagyva köztük. Talán ha nem hagyjuk a számokat „besűrűsödni”, akkor nem üti fel a fejét számtani sorozat, és a végtelenségig játszhatunk.
számok közül, hanem az összes pozitív egész számból válogathatnánk. Az az ember érzése, hogy egyre nagyobb és nagyobb számokat kéne választani, egyre nagyobb réseket hagyva köztük. Talán ha nem hagyjuk a számokat „besűrűsödni”, akkor nem üti fel a fejét számtani sorozat, és a végtelenségig játszhatunk.
Most már csak egyetlen fogalom, ez a bizonyos sűrűség választ el minket a sejtés kimondásától. Legyen 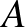 a természetes számoknak egy tetszőleges részhalmaza. Az érdekel minket, hogy hogyan alakul az
a természetes számoknak egy tetszőleges részhalmaza. Az érdekel minket, hogy hogyan alakul az 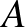 sűrűsége az
sűrűsége az 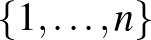 alakú halmazokban, amikor
alakú halmazokban, amikor 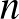 -et egyre nagyobbnak és nagyobbnak választjuk. A sűrűséget egy adott
-et egyre nagyobbnak és nagyobbnak választjuk. A sűrűséget egy adott 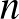 -re a lehető legtermészetesebben mérjük: mekkora hányadát teszi ki az
-re a lehető legtermészetesebben mérjük: mekkora hányadát teszi ki az 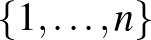 halmaznak az
halmaznak az 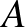 oda eső része
oda eső része 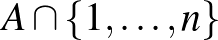 , vagyis mennyi a
, vagyis mennyi a 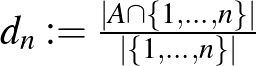 hányados értéke. (Az
hányados értéke. (Az  abszolútérték jel mostantól mindig a halmazok elemszámát jelöli.) Erdős Pál és Turán Pál sejtése azt mondja, hogy ha van olyan pozitív
abszolútérték jel mostantól mindig a halmazok elemszámát jelöli.) Erdős Pál és Turán Pál sejtése azt mondja, hogy ha van olyan pozitív 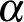 szám szám, hogy a
szám szám, hogy a 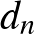 sűrűségek végtelen sokszor fölé mennek
sűrűségek végtelen sokszor fölé mennek 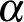 -nak, akkor
-nak, akkor 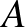 tartalmaz
tartalmaz 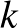 hosszú számtani sorozatot minden
hosszú számtani sorozatot minden 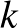 -ra.
-ra.
Maga Erdős azt mesélte a sejtésről (bővebben lásd itt), hogy eleinte nem vették észre, hogy ez egy ennyire nehéz probléma. Később aztán 1000 dollárt ajánlott a bizonyításért, amit Szemerédi 1972-ben megcsinált. Az eredmények cikké formálásában Hajnal András segédkezett, az Amerikában tartózkodó Erdős nála érdeklődött, hogy jó-e a bizonyítás. Hajnal a rá jellemző humorral azt válaszolta, hogy azt még nem tudja, de 500 dollárért már megvenné.

4. ábra. Erdős Pál és Szemerédi Endre (További érdekes fotók itt: I,II.)
A bizonyítás jó volt, az Erdős-Turán sejtést pedig ma már inkább Szemerédi tételnek nevezik. A tétel bizonyítása rettenetesen bonyolult (lásd [6]), és ennek a rettenetesen bonyolult bizonyításnak az egyik lépése az a páros gráfokra vonatkozó segédállítás, amelyből aztán a regularitási lemma később kifejlődött [7].
Mielőtt rátérnénk magára a lemmára, teszünk néhány megjegyzést az Erdős-Turán sejtéssel és a Szemerédi tétellel kapcsolatban. A mai napig nyitott a sejtés egy erősebb változata: igaz-e, hogy ha 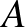 egy olyan részhalmaza a természetes számoknak, amelyre a
egy olyan részhalmaza a természetes számoknak, amelyre a  sor divergens, akkor
sor divergens, akkor 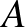 tartalmaz
tartalmaz 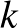 hosszúságú számtani sorozatot minden
hosszúságú számtani sorozatot minden 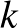 -ra. Mivel Leonhard Euler már 1737-ben bebizonyította, hogy a prímek reciprokösszege divergens (jelölje a továbbiakban a prímek halmazát
-ra. Mivel Leonhard Euler már 1737-ben bebizonyította, hogy a prímek reciprokösszege divergens (jelölje a továbbiakban a prímek halmazát 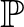 ), ezért aki ezt az erős Erdős-Turán sejtést igazolja, az automatikusan bebizonyítja a számelmélet egyik legősibb sejtését, hogy van tetszőlegesen hosszú prímszámokból álló sorozat. Egyébként ez utóbbi sejtés 2008 óta már tétel, ugyanis Ben Green és Terence Tao bebizonyította [4] (a bizonyítás egyik fő komponense persze maga a Szemerédi tétel), hogy ha
), ezért aki ezt az erős Erdős-Turán sejtést igazolja, az automatikusan bebizonyítja a számelmélet egyik legősibb sejtését, hogy van tetszőlegesen hosszú prímszámokból álló sorozat. Egyébként ez utóbbi sejtés 2008 óta már tétel, ugyanis Ben Green és Terence Tao bebizonyította [4] (a bizonyítás egyik fő komponense persze maga a Szemerédi tétel), hogy ha 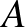 egy olyan prímszámokból álló halmaz, amelyre a
egy olyan prímszámokból álló halmaz, amelyre a  relatív sűrűség végtelen sokszor fölé megy egy
relatív sűrűség végtelen sokszor fölé megy egy 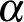 pozitív számnak, akkor
pozitív számnak, akkor 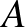 tartalmaz
tartalmaz 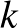 hosszúságú számtani sorozatot minden
hosszúságú számtani sorozatot minden 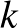 -ra. Világos, hogy ha itt
-ra. Világos, hogy ha itt 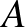 helyére magát
helyére magát 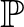 -t helyettesítjük, akkor
-t helyettesítjük, akkor 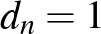 minden
minden 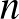 -re, tehát a prímek halmaza valóban tartalmaz tetszőlegesen hosszú számtani sorozatot. Végül egy érdekesség az Abel-díj kapcsán: a 2020-as díjazott Hillél Fürstenberg számtalan híres eredményének egyike a Szemerédi tételre adott ergodelméleti módszereket használó bizonyítás [2].
-re, tehát a prímek halmaza valóban tartalmaz tetszőlegesen hosszú számtani sorozatot. Végül egy érdekesség az Abel-díj kapcsán: a 2020-as díjazott Hillél Fürstenberg számtalan híres eredményének egyike a Szemerédi tételre adott ergodelméleti módszereket használó bizonyítás [2].
2. A regularitási lemma
A regularitási lemma tehát egy gráfelméleti állítás, ami valójában csak nagyon nagy méretű (tehát sok csúccsal és rengeteg éllel rendelkező) gráfokról mond valamit. Mi itt egy kis csalással élve minden fogalmat és állítást kis méretű gráfokon fogunk szemléltetni.
Idézzük fel elsőként, hogy mi a gráf: adottak csúcsok, amelyek közül egyesek össze vannak kötve éllel, mások nincsenek. A csúcsok halmazát 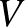 -vel, az élek halmazát
-vel, az élek halmazát 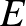 -vel, magát a
-vel, magát a 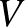 csúcshalmaz és
csúcshalmaz és 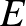 élhalmaz által meghatározott gráfot pedig
élhalmaz által meghatározott gráfot pedig 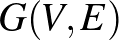 -vel jelöljük.
-vel jelöljük.
Ha 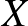 és
és 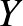 két részhalmaza
két részhalmaza 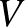 -nek, akkor az
-nek, akkor az 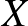 és
és 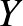 között menő élek számát jelölje
között menő élek számát jelölje 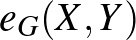 . (Azokat az éleket, amelyeknek mindkét vége
. (Azokat az éleket, amelyeknek mindkét vége  -ban van, kétszer számoljuk.) Számunkra különösen fontosak az úgynevezett páros gráfok: ha a
-ban van, kétszer számoljuk.) Számunkra különösen fontosak az úgynevezett páros gráfok: ha a 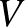 csúcshalmaz felbontható két részre
csúcshalmaz felbontható két részre 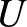 -ra és
-ra és 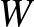 -re úgy, hogy élek csak a különböző csúcsosztályok között mennek, akkor
-re úgy, hogy élek csak a különböző csúcsosztályok között mennek, akkor 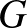 -t páros gráfnak nevezzük és
-t páros gráfnak nevezzük és 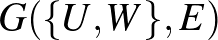 -vel jelöljük.
-vel jelöljük.
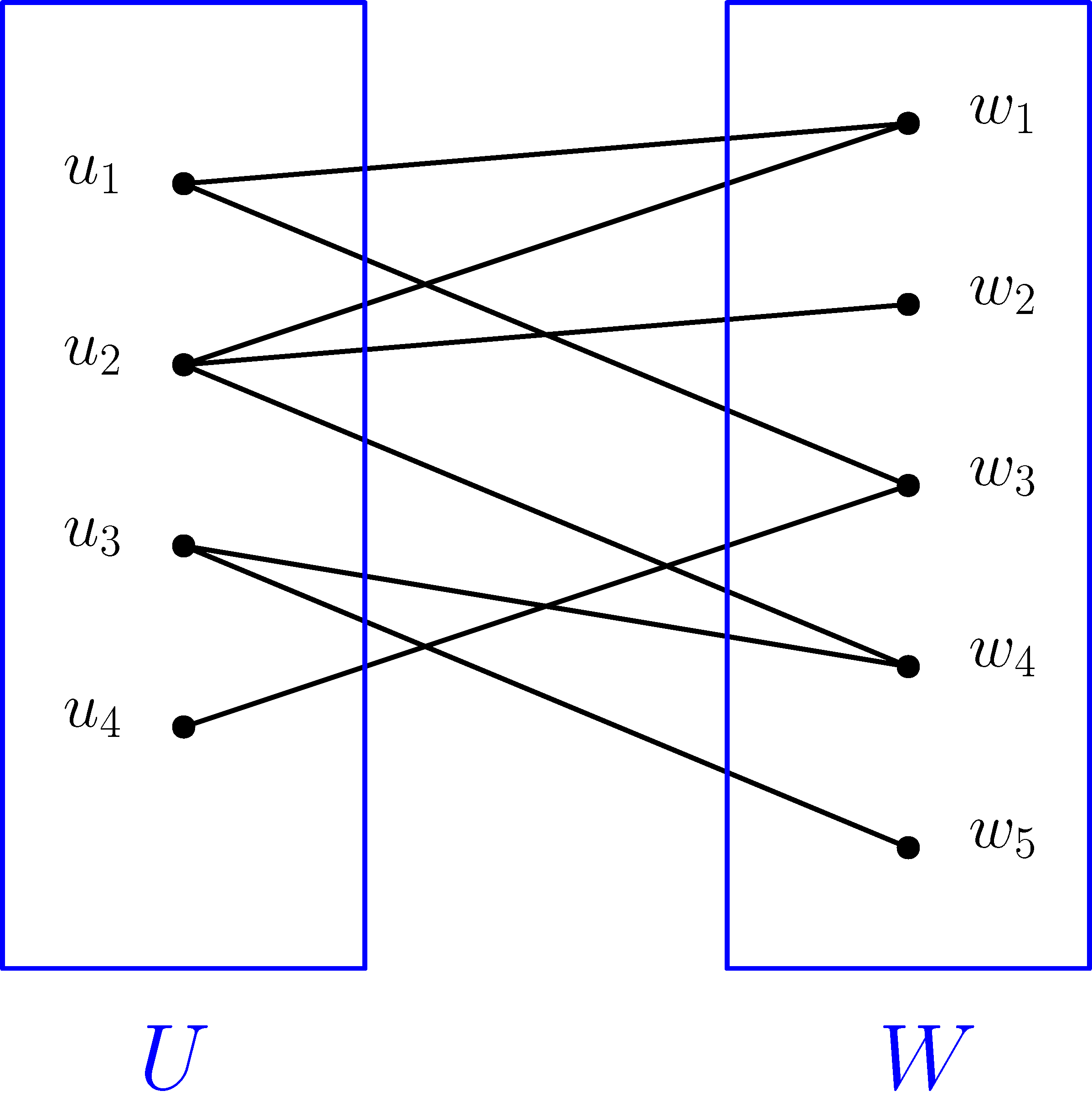
Egy 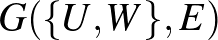 páros gráfban a
páros gráfban a 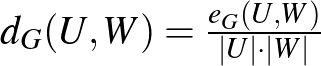 hányadosra gondolhatunk úgy, mint
hányadosra gondolhatunk úgy, mint 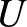 és
és 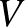 közötti élsűrűségre. A fenti gráfra ez a sűrűség
közötti élsűrűségre. A fenti gráfra ez a sűrűség 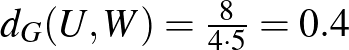 . Ha
. Ha 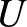 és
és 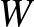 helyett csak az
helyett csak az 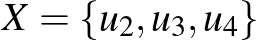 és
és 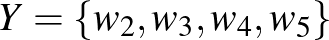 csúcshalmazokat vesszük, és felírjuk az
csúcshalmazokat vesszük, és felírjuk az 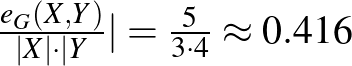 hányadost, akkor egy
hányadost, akkor egy  -hez közeli számot kapunk.
-hez közeli számot kapunk.
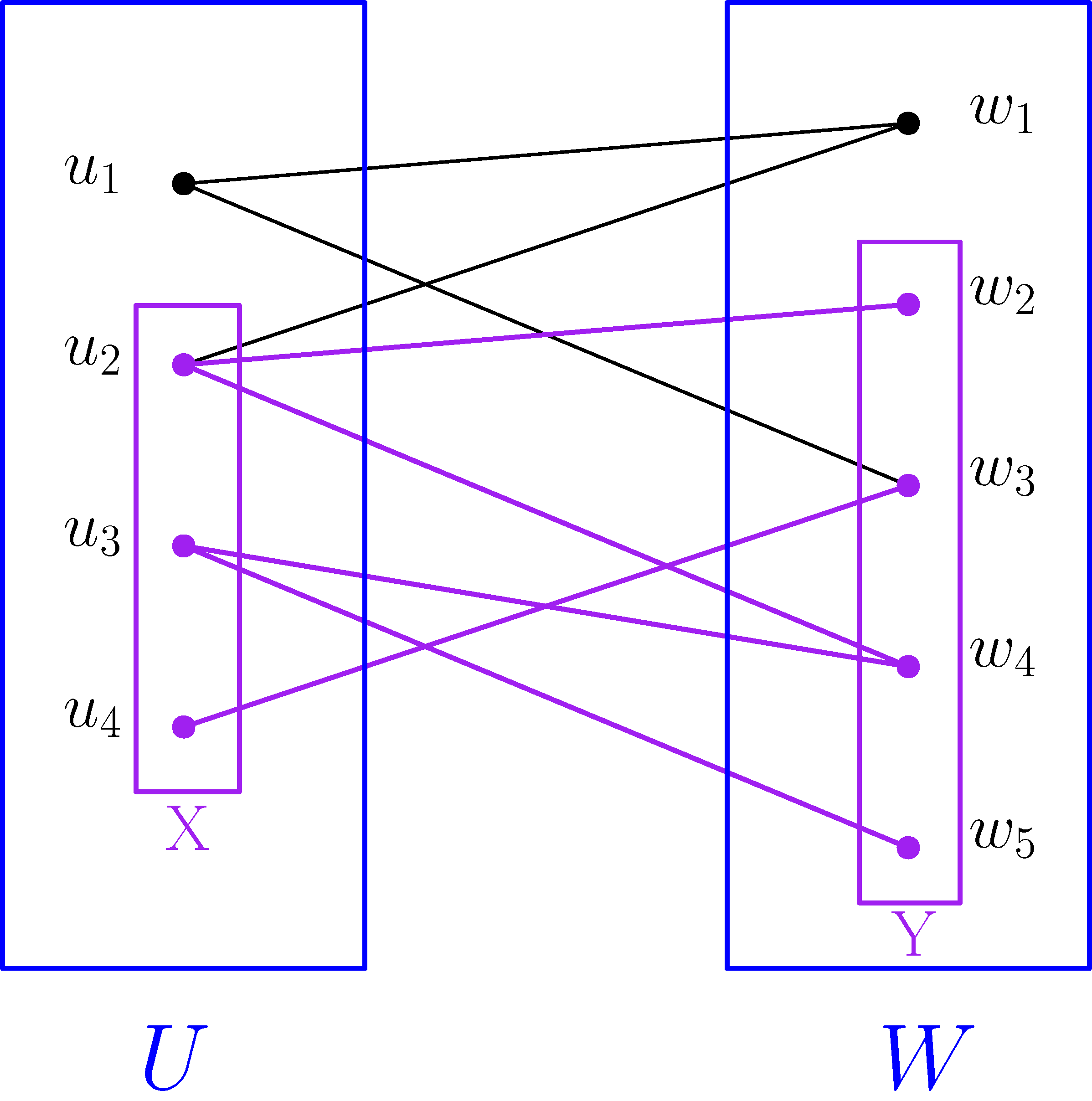
Arra természetesen nem számíthatunk, hogy ez az  és
és 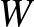 összes részhalmazára igaz: például
összes részhalmazára igaz: például  és
és 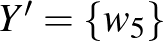 választása esetén
választása esetén 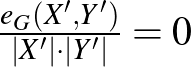 . Vannak azonban olyan gráfok, amikben ha
. Vannak azonban olyan gráfok, amikben ha 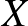 -et és
-et és 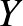 -t elég kövérnek választjuk, akkor
-t elég kövérnek választjuk, akkor 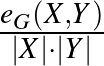 hányados közel van
hányados közel van 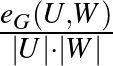 -hez. Ezt a tulajdonságot ragadja meg az
-hez. Ezt a tulajdonságot ragadja meg az 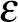 -reguláris páros gráf fogalma.
-reguláris páros gráf fogalma.
A 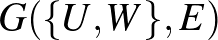 páros gráfot
páros gráfot 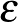 -regulárisnak nevezzük (itt
-regulárisnak nevezzük (itt 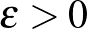 egy rögzített pozitív szám, a megengedett hiba), ha minden olyan
egy rögzített pozitív szám, a megengedett hiba), ha minden olyan 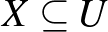 és
és 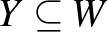 részhalmazra, amelyekre
részhalmazra, amelyekre 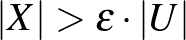 és
és 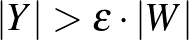 teljesül, a sűrűségek egymáshoz
teljesül, a sűrűségek egymáshoz 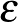 -nál közelebb vannak, azaz
-nál közelebb vannak, azaz
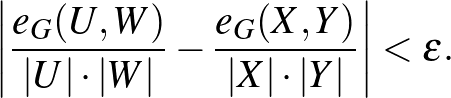
Legyen most  egy tetszőleges gráf (nem feltétlenül páros, mint eddig). Vegyük a
egy tetszőleges gráf (nem feltétlenül páros, mint eddig). Vegyük a  -nek két olyan
-nek két olyan  -sel és
-sel és  -vel jelölt részhalmazát, amelyeknek nincs közös eleme (az alábbi gráfon ezek
-vel jelölt részhalmazát, amelyeknek nincs közös eleme (az alábbi gráfon ezek 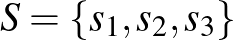 és
és 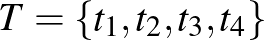 ). Tartsuk meg azokat és csak azokat az éleket, amelyeknek egyik végpontja
). Tartsuk meg azokat és csak azokat az éleket, amelyeknek egyik végpontja  -ben, a másik
-ben, a másik 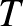 -ben van (az ábrán ez a zöld élhalmaz). Így
-ben van (az ábrán ez a zöld élhalmaz). Így 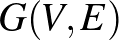 -nek egy olyan részgráfját kapjuk, ami páros. Jelölje ezt
-nek egy olyan részgráfját kapjuk, ami páros. Jelölje ezt ![$G[S,T]$](/images/stories/latexuj/2021-05/2021-05-titkostamasregularitasilemma/img71.png) .
.
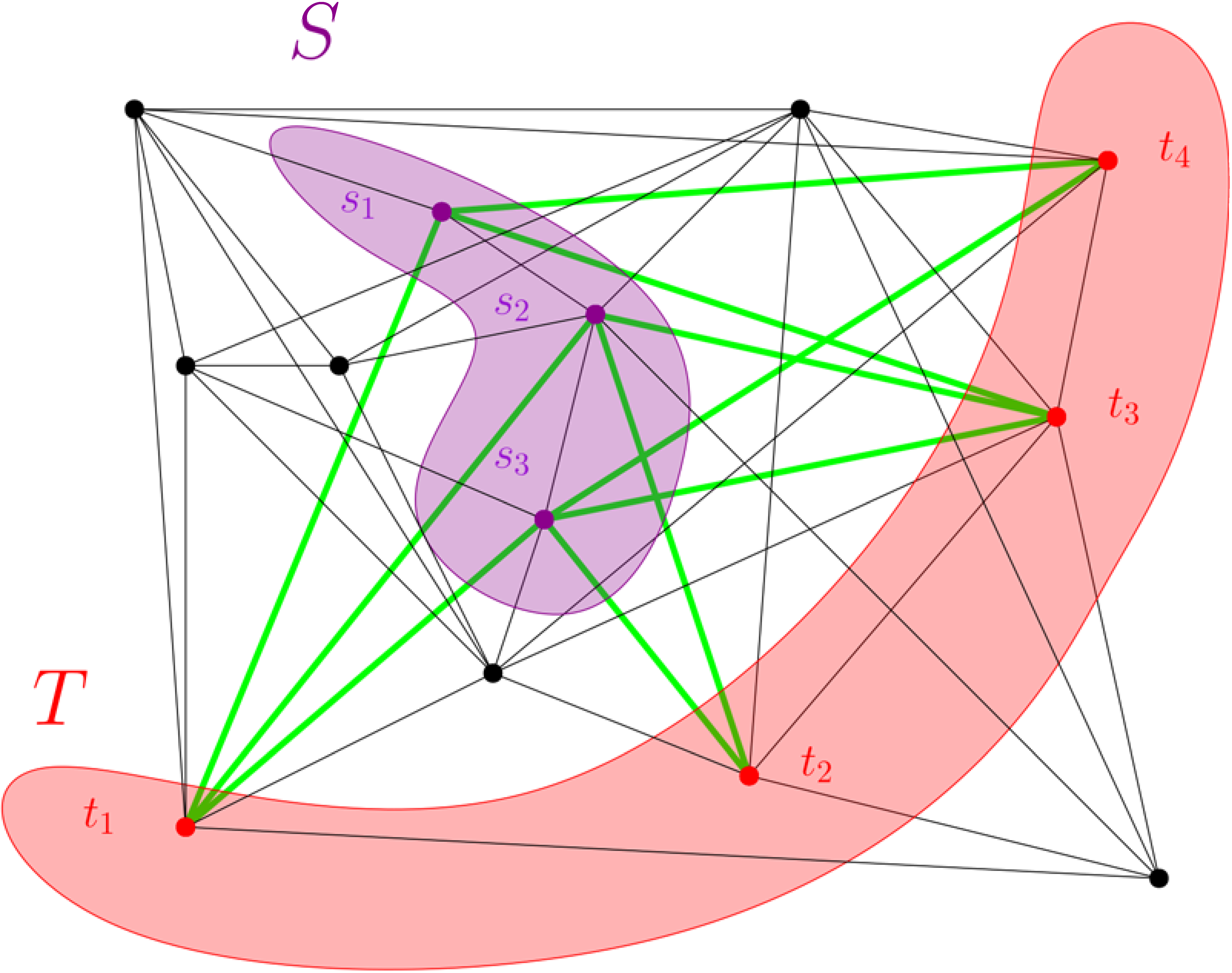
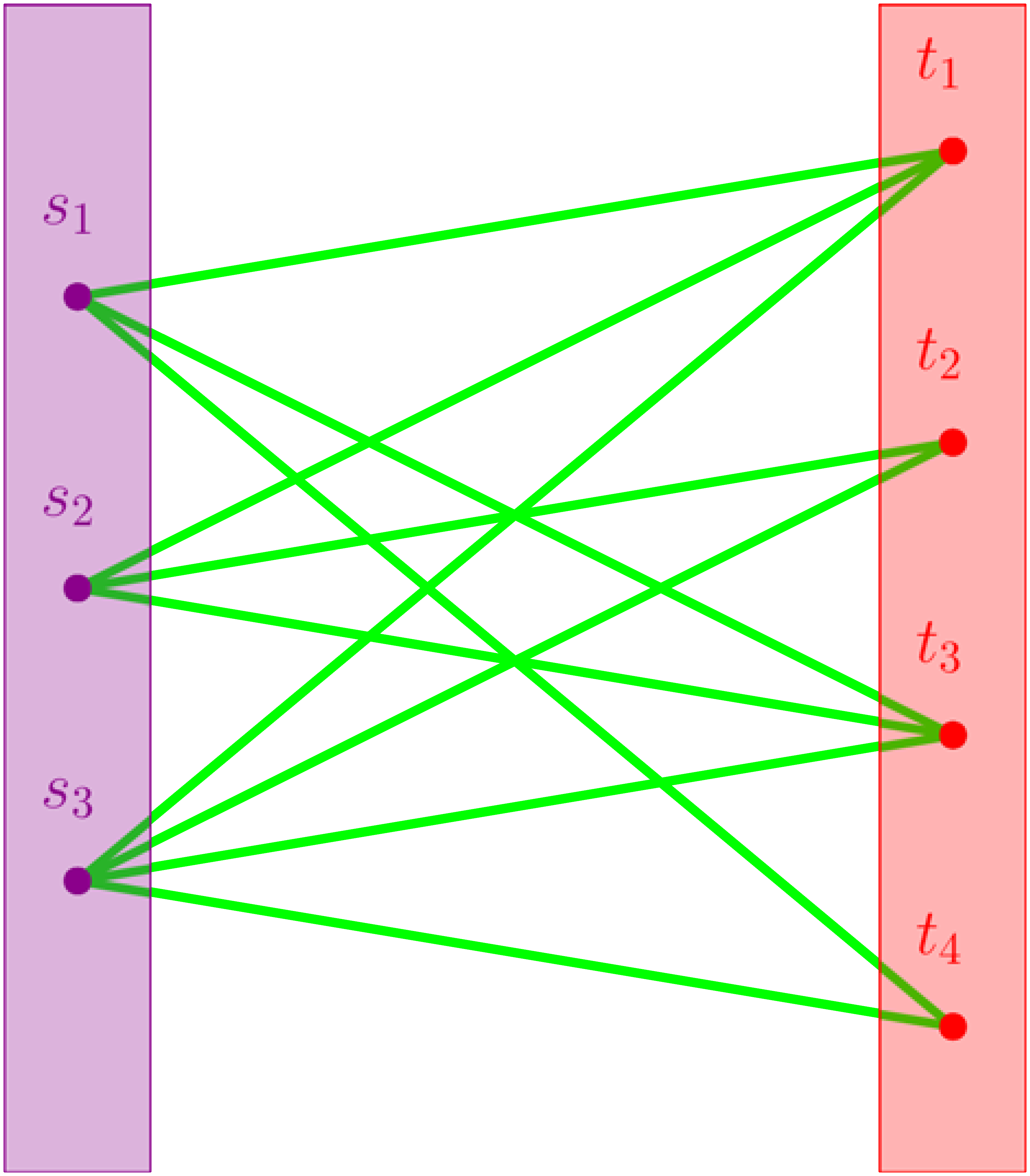
Nagyon pongyolán fogalmazva a regularitási lemma azt mondja, hogy ha a gráfnak elég sok csúcsa van, akkor a csúcsokat fel tudjuk bontani kevés darab lényegében egyforma méretű 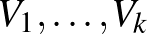 halmazra úgy, hogy ha ezekből készítjük el a
halmazra úgy, hogy ha ezekből készítjük el a ![$G[V_i,V_j]$](/images/stories/latexuj/2021-05/2021-05-titkostamasregularitasilemma/img74.png) páros gráfokat a fenti módon, akkor azok nagy része
páros gráfokat a fenti módon, akkor azok nagy része  -reguláris lesz. Tehát a gráfot fel lehet darabolni nem túl sok „szép darabra”, persze némi hibától eltekintve.
-reguláris lesz. Tehát a gráfot fel lehet darabolni nem túl sok „szép darabra”, persze némi hibától eltekintve.
A rend kedvéért precízen is kimondjuk a lemma klasszikus alakját, továbbá egy gyenge alakját is, mert később ezek majd jól fognak jönni. Ehhez szükségünk lesz a partíció fogalmára. A 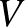 csúcshalmaz egy
csúcshalmaz egy 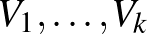 átfedés nélküli halmazokra való feldarabolását partíciónak nevezzük.
átfedés nélküli halmazokra való feldarabolását partíciónak nevezzük.

Ha a partícióban szereplő darabok lényegében egyforma méretűek, azaz 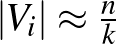 minden
minden 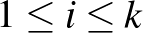 -ra (másképp:
-ra (másképp: 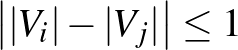 ), akkor a partíciót ekvipartíciónak nevezzük.
), akkor a partíciót ekvipartíciónak nevezzük.
1. Lemma. (Regularitási lemma, hagyományos alak.) Tetszőleges 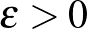 és
és  számokhoz léteznek olyan
számokhoz léteznek olyan 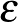 -tól és
-tól és 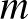 -től függő
-től függő 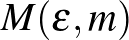 és
és 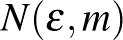 konstansok, amelyekre az alábbi állítás teljesül. Minden legalább
konstansok, amelyekre az alábbi állítás teljesül. Minden legalább 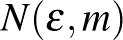 csúcsú gráf csúcshalmazának van olyan
csúcsú gráf csúcshalmazának van olyan 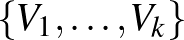 ekvipartíciója (
ekvipartíciója ( 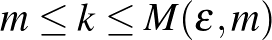 ), amelyben legfeljebb
), amelyben legfeljebb 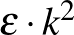 darab
darab 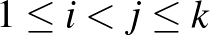 indexpár kivételével mindegyik
indexpár kivételével mindegyik ![$G[V_i,V_j]$](/images/stories/latexuj/2021-05/2021-05-titkostamasregularitasilemma/img74.png) páros gráf
páros gráf 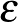 -reguláris.
-reguláris.
Most rátérünk a regularitási lemma egy gyenge alakjára, ami Alan Frieze-től és Ravi Kannantól származik [1]. Hasonlóan a korábbi 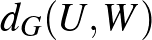 mennyiséghez, vezessük be a partícióhoz tartozó élsűrűségeket. Egy adott
mennyiséghez, vezessük be a partícióhoz tartozó élsűrűségeket. Egy adott 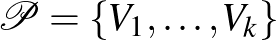 partíció esetén jelölje
partíció esetén jelölje 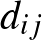 a
a 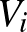 és
és 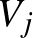 csúcshalmazok közti élsűrűséget:
csúcshalmazok közti élsűrűséget:
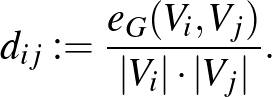
Legyen  és
és  a
a  -nek két részhalmaza. Emlékezzünk, hogy
-nek két részhalmaza. Emlékezzünk, hogy 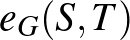 -vel jelöltük azon élek számát, amelyeknek egyik végpontja
-vel jelöltük azon élek számát, amelyeknek egyik végpontja  -ben, a másik
-ben, a másik 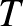 -ben van. Ezt az
-ben van. Ezt az 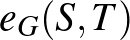 mennyiséget megbecsülhetjük a
mennyiséget megbecsülhetjük a  partíció és a
partíció és a 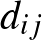 sűrűségek (vagy ha úgy tetszik átlagok) segítségével:
sűrűségek (vagy ha úgy tetszik átlagok) segítségével:
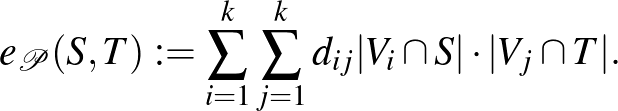
Mivel átlagokkal számoltunk, természetesen nem várhatjuk, hogy tetszőleges  -re és
-re és 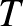 -re
-re 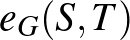 megegyezzen
megegyezzen 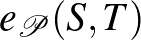 -vel. Az eltérés nagyságra, tehát a
-vel. Az eltérés nagyságra, tehát a 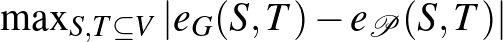 számra tekinthetünk úgy, mint egy mérőszámra, ami a
számra tekinthetünk úgy, mint egy mérőszámra, ami a 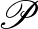 partíció irregularitását méri. Most már minden adott, hogy kimondjuk a regularitási lemma gyenge alakját. (Ennek a gyenge alaknak a következő fejezetben komoly szerepe lesz.)
partíció irregularitását méri. Most már minden adott, hogy kimondjuk a regularitási lemma gyenge alakját. (Ennek a gyenge alaknak a következő fejezetben komoly szerepe lesz.)
2. Lemma. (Gyenge regularitási lemma.) Tetszőleges 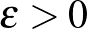 számhoz és tetszőleges
számhoz és tetszőleges 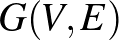 gráfhoz van olyan
gráfhoz van olyan 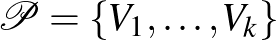 (
( 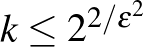 ) partíciója
) partíciója 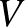 -nek, hogy minden
-nek, hogy minden 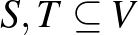 -re
-re
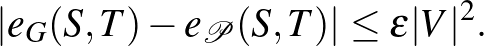
3. Regularitási lemma az analízisben
Már említettük Lovász László és Szegedy Balázs Szemerédi's Lemma for the Analyst című cikkét, amelyben a regularitási lemmának három különböző analízisbeli interpretációját is megadták. Különösen érdekes ez az eredmény, mert a gráfelmélet és az analízis között (vagy ha úgy tetszik a folytonos és diszkrét matematika között) hatalmas szakadékot kell tudni áthidalni. Az ilyen távoli területek összekapcsolása mindig nagyon szép, és persze roppant bonyolult. Arra nincs lehetőség, hogy a szükséges fogalmakat mind bevezessük, és a cikk eredményeit itt bemutassuk, de talán sikerül legalább a felszínt megkapargatni.
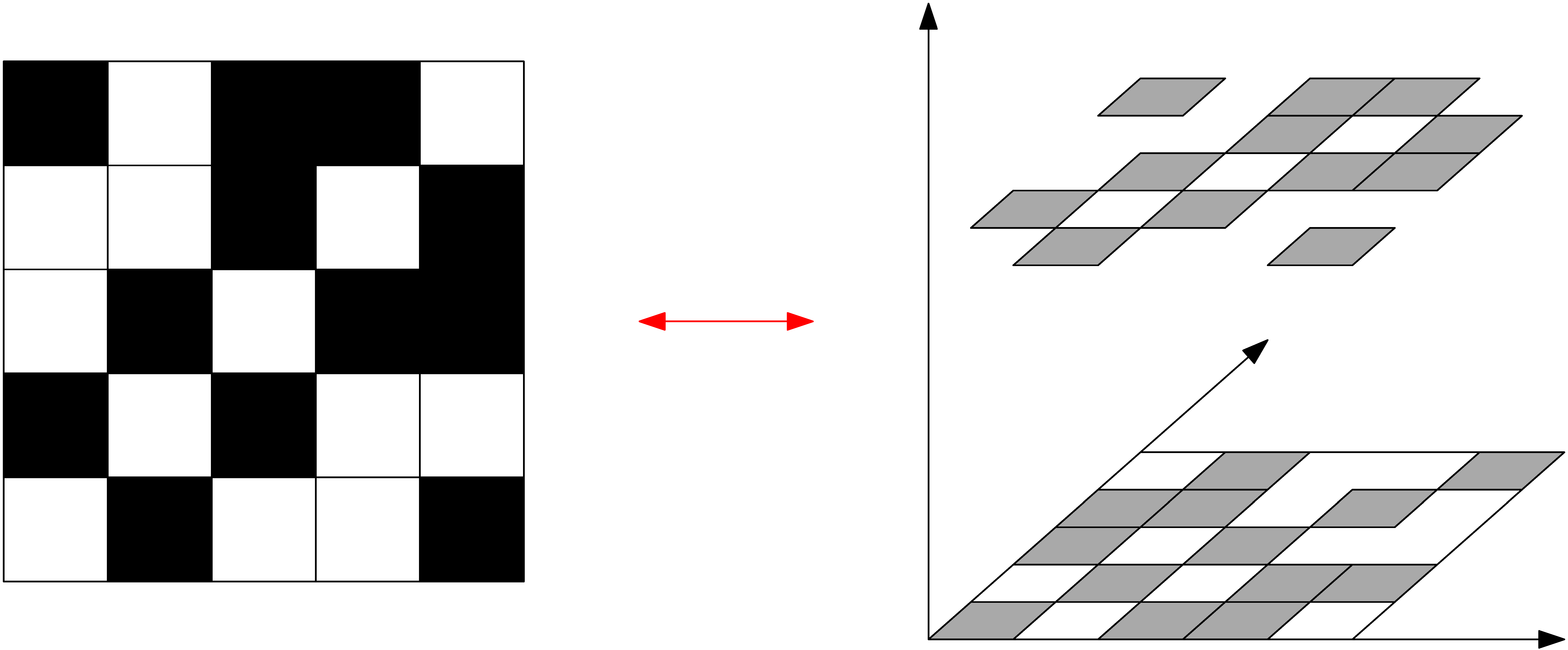
Először arról lesz szó, hogy hogyan lehet gráfokat speciális függvényekkel azonosítani. A példa kedvéért vegyük az alábbi ötcsúcsú 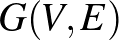 gráfot, és mellé egy
gráfot, és mellé egy 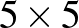 egybevágó négyzetre felbontott egységnégyzetet. Számozzuk meg a csúcsokat, és feketítsük be az
egybevágó négyzetre felbontott egységnégyzetet. Számozzuk meg a csúcsokat, és feketítsük be az  -edik oszlop és
-edik oszlop és 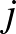 -edik sor kereszteződésében lévő négyzetet, ha az
-edik sor kereszteződésében lévő négyzetet, ha az  és
és 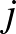 csúcsok szomszédosak. (Azon se most, se később ne akadjunk fenn, hogy a szomszédos kis négyzetek közös oldala milyen színű, ha az egyik négyzet fekete, a másik pedig fehér.)
csúcsok szomszédosak. (Azon se most, se később ne akadjunk fenn, hogy a szomszédos kis négyzetek közös oldala milyen színű, ha az egyik négyzet fekete, a másik pedig fehér.)

Ezzel az eljárással egy felcímkézett gráfot megfeleltettünk egy „pixeles képnek”. A pixeles képet pedig meg tudjuk feleltetni egy ![$W:[0,1]\times[0,1]\to[0,1]$](/images/stories/latexuj/2021-05/2021-05-titkostamasregularitasilemma/img104.png) függvénynek: legyen
függvénynek: legyen 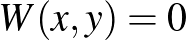 , ha az
, ha az 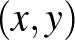 pont a pixeles képen fehér, és legyen
pont a pixeles képen fehér, és legyen 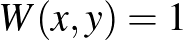 , ha az
, ha az 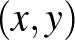 pont a pixeles képen fekete színű.
pont a pixeles képen fekete színű.
Mivel a szomszédosság egy szimmetrikus reláció (ha az 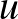 csúcs össze van kötve
csúcs össze van kötve 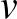 -vel, akkor
-vel, akkor 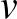 is össze van kötve
is össze van kötve 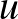 -val), ezért a fenti eljárással definiált függvények szimmetrikusak, azaz minden
-val), ezért a fenti eljárással definiált függvények szimmetrikusak, azaz minden  -re
-re 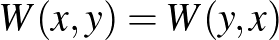 . Most áttérünk egy jóval általánosabb függvényosztályra, ami ezeket a pixeles képekből származó függvényeket mind tartalmazza.
. Most áttérünk egy jóval általánosabb függvényosztályra, ami ezeket a pixeles képekből származó függvényeket mind tartalmazza.
Jelöljük 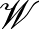 -vel a
-vel a ![$W:[0,1]\times[0,1]\to\mathbb{R}$](/images/stories/latexuj/2021-05/2021-05-titkostamasregularitasilemma/img114.png) korlátos és mérhető szimmetrikus függvények vektorterét. Egy
korlátos és mérhető szimmetrikus függvények vektorterét. Egy 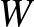 függvény korlátossága alatt azt értjük, hogy van olyan
függvény korlátossága alatt azt értjük, hogy van olyan 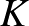 szám, amire
szám, amire 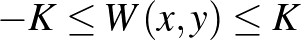 teljesül minden
teljesül minden 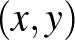 pontra. A mérhetőség pedig egy nagyon természetes (és szükséges) technikai feltevés, amennyiben az ember integrálni szeretne. Márpedig hamarosan látni fogjuk, hogy az integrál fogalma mindig ott lesz a háttérben. A részletekbe terjedelmi okokból nem megyünk bele, elégedjünk meg annyival, hogy ezzel a mérhetőségi feltevéssel csak olyan (vadul viselkedő) függvényeket zárunk ki, amelyek úgy képezik a
pontra. A mérhetőség pedig egy nagyon természetes (és szükséges) technikai feltevés, amennyiben az ember integrálni szeretne. Márpedig hamarosan látni fogjuk, hogy az integrál fogalma mindig ott lesz a háttérben. A részletekbe terjedelmi okokból nem megyünk bele, elégedjünk meg annyival, hogy ezzel a mérhetőségi feltevéssel csak olyan (vadul viselkedő) függvényeket zárunk ki, amelyek úgy képezik a ![$[0,1]\times[0,1]$](/images/stories/latexuj/2021-05/2021-05-titkostamasregularitasilemma/img117.png) -et
-et 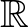 -be, hogy a rajtuk lévő természetes halmazstruktúrák a függvény mentén nem passzolnak össze.
-be, hogy a rajtuk lévő természetes halmazstruktúrák a függvény mentén nem passzolnak össze.
A 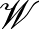 vektorteret felruházhatjuk egy speciális függvénnyel, a vágás norma nevű mennyiséggel. Minden
vektorteret felruházhatjuk egy speciális függvénnyel, a vágás norma nevű mennyiséggel. Minden 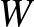 függvényhez rendeljünk hozzá egy
függvényhez rendeljünk hozzá egy 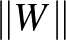 -val jelölt számot, az ő normáját a következő formulával
-val jelölt számot, az ő normáját a következő formulával
![$\displaystyle \Vert W\Vert:=\sup_{S,T\subseteq[0,1]}\left\vert\int\limits_{S\times T}W(x,y)~dxdy\right\vert.
$](/images/stories/latexuj/2021-05/2021-05-titkostamasregularitasilemma/img120.png)
A normára gondolhatunk úgy, mint a hosszúság fogalmának egy nagyon fontos és hasznos általánosítására. Ha rendelkezésünkre áll egy norma, akkor olyan absztrakt fogalmakat is megfoghatunk számok segítségével, mint például a „közelség”. Azt mondhatjuk, hogy 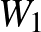 és
és 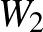 közel vannak egymáshoz, vagy kevéssel térnek el egymástól, ha a különbségüknek kicsi a hossza, azaz ha a
közel vannak egymáshoz, vagy kevéssel térnek el egymástól, ha a különbségüknek kicsi a hossza, azaz ha a 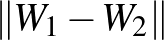 szám kicsi.
szám kicsi.
Észrevehettük, hogy a gráfokhoz tartozó függvények elég speciális szerkezetűek. Valóban, ezek a függvények az úgynevezett lépcsős függvények osztályához tartoznak. Egy 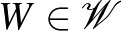 függvényt lépcsős függvénynek nevezünk legfeljebb
függvényt lépcsős függvénynek nevezünk legfeljebb 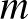 lépcsővel, ha van a
lépcsővel, ha van a ![$[0,1]$](/images/stories/latexuj/2021-05/2021-05-titkostamasregularitasilemma/img125.png) intervallumnak olyan
intervallumnak olyan  felosztása, hogy a
felosztása, hogy a 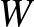 függvény konstans az összes
függvény konstans az összes 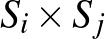 téglán.
téglán.

Azt láttuk, hogy egy 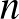 csúcsú gráfot olyan szimmetrikus lépcsős függvénnyel tudtunk azonosítani, amelyben a
csúcsú gráfot olyan szimmetrikus lépcsős függvénnyel tudtunk azonosítani, amelyben a  partíció tagjai az
partíció tagjai az  hosszú intervallumok az
hosszú intervallumok az 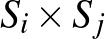 négyzeteken pedig a függvényérték vagy 0 vagy 1.
négyzeteken pedig a függvényérték vagy 0 vagy 1.
Egy másik fontos függvényosztály a 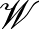 azon elemeiből áll, amelyekre
azon elemeiből áll, amelyekre 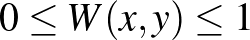 teljesül minden
teljesül minden ![$(x,y)\in[0,1]\times[0,1]$](/images/stories/latexuj/2021-05/2021-05-titkostamasregularitasilemma/img131.png) esetén. Ezeket a függvényeket grafonoknak nevezzük, a grafonok halmazát pedig
esetén. Ezeket a függvényeket grafonoknak nevezzük, a grafonok halmazát pedig 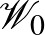 -lal jelöljük. A regularitási lemma gyenge alakjának (lásd 2. Lemma) analitikus változata azt mondja, hogy bármilyen
-lal jelöljük. A regularitási lemma gyenge alakjának (lásd 2. Lemma) analitikus változata azt mondja, hogy bármilyen 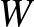 grafont is veszünk, és bármilyen kicsi
grafont is veszünk, és bármilyen kicsi 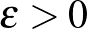 hibát engedünk meg, találunk majd olyan
hibát engedünk meg, találunk majd olyan 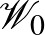 -beli lépcsős grafont, amely a
-beli lépcsős grafont, amely a 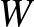 -t
-t 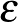 -nál jobban megközelíti, és nincs túl sok lépcsője.
-nál jobban megközelíti, és nincs túl sok lépcsője.
3. Lemma. (Gyenge regularitási lemma, analitikus változat.) Minden 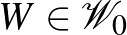 grafonhoz és
grafonhoz és 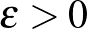 -hoz létezik olyan
-hoz létezik olyan 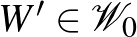 lépcsős függvény legfeljebb
lépcsős függvény legfeljebb 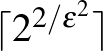 lépcsővel, amelyre
lépcsővel, amelyre 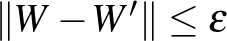 .
.
Végezetül megemlítjük, hogy a regularitási lemma megfogalmazható mint kompaktsági tétel. Ezt a mély állítást a többinél kicsit tömörebben, az analízisben sztendernek számító fogalmak felidézése nélkül tárgyaljuk. Tudjuk, hogy egy topologikus tér metrizálhatósága mennyire fontos és hasznos tulajdonság, különösen ha a metrizálással nyert metrikus tér kompakt. A kérdés, hogy hogyan metrizáljuk a grafonok terét, és hogy a metrizálással kapott tér kompakt-e.
Először is egy megjegyzés: az az eljárás, ahogy gráfokból függvényeket csináltunk, függött attól, hogy hogyan címkéztük fel a csúcsokat. A következő példa azt mutatja, hogy ugyanannak az ötcsúcsú (címkézetlen) gráfnak két különböző önkényes felcímkézése különböző pixeles képekhez, és így különböző függvényekhez vezet.

A csúcsok átszámozásának megfelelője a grafonok nyelvén egy ![$\varphi:[0,1]\to[0,1]$](/images/stories/latexuj/2021-05/2021-05-titkostamasregularitasilemma/img138.png) invertálható mértéktartó leképzéssel való komponálás, nevezetesen
invertálható mértéktartó leképzéssel való komponálás, nevezetesen 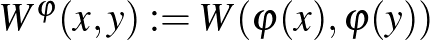 . Vezessük be az alábbi
. Vezessük be az alábbi 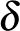 függvényt a vágás norma segítségével
függvényt a vágás norma segítségével  .
.
Ez a 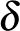 már majdnem egy metrika, ráadásul úgy méri a grafonok távolságát, hogy az az „átcímkézésre” érzéketlen. Meg lehet mutatni, hogy
már majdnem egy metrika, ráadásul úgy méri a grafonok távolságát, hogy az az „átcímkézésre” érzéketlen. Meg lehet mutatni, hogy 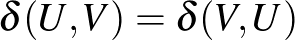 , és hogy
, és hogy 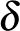 teljesíti a háromszögegyenlőtlenséget
teljesíti a háromszögegyenlőtlenséget 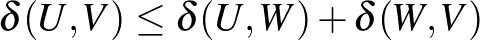 . Azonban a
. Azonban a 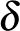 definíciójából adódóan itt most azzal a problémával szembesülünk, hogy vannak olyan
definíciójából adódóan itt most azzal a problémával szembesülünk, hogy vannak olyan 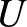 és
és 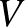 grafonok, amik nem azonosak, a
grafonok, amik nem azonosak, a 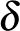 -távolságuk mégis nulla. Márpedig azt meg akarjuk követelni, hogy a metrizálandó objektumaink csak önmaguktól legyenek nulla távolságra. Mivel az
-távolságuk mégis nulla. Márpedig azt meg akarjuk követelni, hogy a metrizálandó objektumaink csak önmaguktól legyenek nulla távolságra. Mivel az 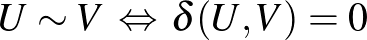 reláció nyilvánvalóan egy ekvivalencia reláció, ezért ezeket az egymástól nulla távolságra lévő elemeket azonosíthatjuk. Jelöljük az így kapott teret
reláció nyilvánvalóan egy ekvivalencia reláció, ezért ezeket az egymástól nulla távolságra lévő elemeket azonosíthatjuk. Jelöljük az így kapott teret 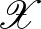 -szel. Erre az
-szel. Erre az 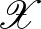 -re a
-re a 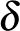 -t ráhúzva már egy valódi metrikus teret kapunk.
-t ráhúzva már egy valódi metrikus teret kapunk.
Térjünk rá a kompaktságra: metrikus terekben a kompaktság ekvivalens a sorozatkompaktsággal, azaz azzal, hogy minden sorozatnak van konvergens részsorozata. Ha tehát adott grafonoknak egy 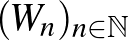 sorozata, akkor konstruálni kell egy olyan
sorozata, akkor konstruálni kell egy olyan 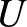 grafont, és
grafont, és 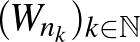 részsorozatot, amelyre
részsorozatot, amelyre  . Lovász és Szegedy a gyenge regularitási lemma analitikus változatának segítségével ezt megtették, ezzel bebizonyították, hogy az
. Lovász és Szegedy a gyenge regularitási lemma analitikus változatának segítségével ezt megtették, ezzel bebizonyították, hogy az 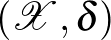 metrikus tér kompakt. Ilyen értelemben a grafonok terének kompaktsága tekinthető úgy, mint a regularitási lemma egy topologikus interpretációja. További részletek, és a regularitási lemma további nagyon érdekes alakjai megtalálhatók a [5] cikkben.
metrikus tér kompakt. Ilyen értelemben a grafonok terének kompaktsága tekinthető úgy, mint a regularitási lemma egy topologikus interpretációja. További részletek, és a regularitási lemma további nagyon érdekes alakjai megtalálhatók a [5] cikkben.

5. ábra. Lovász László és Szegedy Balázs Oberwolfachban
Ahogy arra néhány példát is láthattunk, a Szemerédi regularitási lemmát és a Szemerédi tételt sokan általánosították, újrabizonyították, vagy épp más struktúrákban találtak hasonló eredményeket. Ha az ember kutakodni kezd a regularitási lemma után, azt tapasztalja hogy ahány helyre benéz, annyi variációval találkozik. Ez persze nem olyan meglepő, ugyanis a regularitási lemma sokkal több, mint egy egyszerű merev állítás, a regularitási lemma egy nagyon általános jelenség lényegét ragadja meg. Hogy mi is ez a jelenség? Szemerédi Endre Abel-előadásának címe „In every chaos there is an order” volt, Kepes András róla szóló fantasztikus portréfilmjének címe pedig „Rend a káoszban”, tehát nem lehet kapufát lőni azzal a kompakt megfogalmazással, hogy minden káoszban van valami rendszer.
Irodalomjegyzék
- [1] A. Frieze, R. Kannan, Quick Approximation to Matrices and Applications, Combinatorica 19 (1999), 175–220.
[2] H. Furstenberg, Ergodic behavior of diagonal measures and a theorem of Szemerédi on arithmetic progressions, J. Anal. Math. 31 (1977), 204–256.
[3] T. Gowers, Hypergraph regularity and the multidimensional Szemerédi theorem, Ann. of Math. 166 (3), 897–946.
[4] B. Green, T. Tao, The primes contain arbitrarily long arithmetic progressions, Ann. of Math. 167 (2008), 481–547.
[5] L. Lovász, B. Szegedy, Szemerédi’s Lemma for the Analyst, Geom. Funct. Anal. 17 (2007), 252–270.
[6] E. Szemerédi, On sets of integers containing no 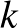 elements in arithmetic progression, Collection of articles in memory of Jurii Vladimirovic Linnik, Acta Arith. 27 (1975), 199–245.
elements in arithmetic progression, Collection of articles in memory of Jurii Vladimirovic Linnik, Acta Arith. 27 (1975), 199–245.
[7] E. Szemerédi, Regular partitions of graphs, Problémes combinatoires et théorie des graphes (Colloq. Internat. CNRS, Univ. Orsay, Orsay, 1976), Colloq. Internat. CNRS, 260, CNRS, Paris, 1978, 399–401.
[8] T. Tao, Szemerédi’s regularity lemma revisited, Contrib. Discrete Math. 1 (2006), 8–28.
A cikk az ITM és az NKFIH ÚNKP-20-5-BGE-1 és PD128374 kódszámú projektjeinek, valamint az MTA Bolyai János Kutatási Ösztöndíjának támogatásával készült.









