Lovász László igen gazdag matematikai munkásságának egyik gyöngyszeme a lokális lemma. Jelentőségét felhasználásainak rendkívül nagy száma adja. Magát a lemmát sokan sok irányban általánosították és nagyon sok kombinatorikai (és néhány azon kívüli) probléma megoldásában játszott kulcsszerepet. Mindezen felül azért is választottam a friss Abel-díjas Lovász gyönyörű eredményei közül pont ezt a jelen cikk témájául, mert bizonyítása egyszerű és csak elemi módszereket használ, így a lemma legegyszerűbb formájának teljes bizonyítását megmutathatom.
Előbb azonban néhány szó a háttérről. Kombinatorikában gyakori jelenség, hogy valamilyen struktúra létezését úgy tudjuk bizonyítani, hogy azt látjuk be, hogy egy véletlen struktúra nagy eséllyel megfelelő lesz, miközben egyetlen konkrét ilyen struktúrát sem tudunk explicit módon megadni. Erre dolgozta ki Erdős Pál az úgynevezett véletlen módszert. Claude Shannon is használt hasonló technikát információelméletben. Módszerük nagyon széles körben bizonyult hatékonynak. Például ezzel látták be olyan nagy kromatikus számú gráfok létezését, amelyeknek a legrövidebb köre is hosszú, szintén így látták be kis fokú ún. expandergráfok létezését, valamint nagy Ramsey-gráfokét, amikre még visszatérünk.
Lássunk egy példát. Tegyük fel, hogy adott egy 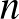 elemű
elemű 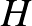 alaphalmaz
alaphalmaz 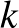 elemű részhalmazainak egy
elemű részhalmazainak egy  rendszere. Egy ilyen rendszert
rendszere. Egy ilyen rendszert 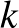 -uniform hipergráfnak is hívnak,
-uniform hipergráfnak is hívnak, 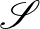 elemei a hiperélek. Ki szeretnénk színezni
elemei a hiperélek. Ki szeretnénk színezni 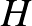 elemeit két színnel úgy, hogy egyetlen hiperél se legyen egyszínű. Ezt a problémát hívják hipergráf kétszínezési problémának. Ahelyett, hogy egy algoritmust adnánk erre, tekintünk egy véletlen színezést (azaz minden elemet a többitől függetlenül egyenlő eséllyel színezünk a két szín egyikére vagy másikára). Vizsgáljuk meg annak a valószínűségét, hogy lesz egy egyszínű hiperél. Egy fix
elemeit két színnel úgy, hogy egyetlen hiperél se legyen egyszínű. Ezt a problémát hívják hipergráf kétszínezési problémának. Ahelyett, hogy egy algoritmust adnánk erre, tekintünk egy véletlen színezést (azaz minden elemet a többitől függetlenül egyenlő eséllyel színezünk a két szín egyikére vagy másikára). Vizsgáljuk meg annak a valószínűségét, hogy lesz egy egyszínű hiperél. Egy fix 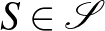 hiperélet
hiperélet 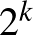 féleképpen színezhetünk, ezek esélye egyenlő, de csak kettő esetben lesz
féleképpen színezhetünk, ezek esélye egyenlő, de csak kettő esetben lesz 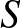 egyszínű, így ennek valószínűsége
egyszínű, így ennek valószínűsége 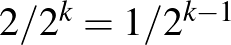 . Annak a valószínűsége, hogy valamelyik hiperél egyszínű, legfeljebb
. Annak a valószínűsége, hogy valamelyik hiperél egyszínű, legfeljebb 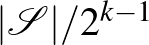 . Ez nem pontos érték, mert bizonyos színezéseknél több hiperél is egyszínű lesz (így ezeket a színezéseket „többször számoljuk”), de felső becslésnek megfelelő. Ha
. Ez nem pontos érték, mert bizonyos színezéseknél több hiperél is egyszínű lesz (így ezeket a színezéseket „többször számoljuk”), de felső becslésnek megfelelő. Ha 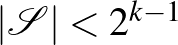 , akkor az előbbi valószínűség 1 alatt van, tehát létezik megfelelő kétszínezés.
, akkor az előbbi valószínűség 1 alatt van, tehát létezik megfelelő kétszínezés.
Lássuk ennek az egyszerű eredménynek egy alkalmazását is. Egy gráfban csúcsok egy halmaza klikket alkot, ha közöttük minden él be van húzva, míg függetlennek nevezzük csúcsok egy halmazát, ha egyetlen él sincs köztük. Ramsey híres tétele alapján minden 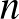 csúcsú gráfban vagy van egy körülbelül
csúcsú gráfban vagy van egy körülbelül 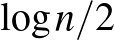 elemű klikk, vagy egy ekkora független halmaz. (A cikkben
elemű klikk, vagy egy ekkora független halmaz. (A cikkben 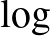 mindig a kettes alapú logaritmust jelöli.) De vajon éles-e ez az eredmény? Nem ismert konstrukció olyan
mindig a kettes alapú logaritmust jelöli.) De vajon éles-e ez az eredmény? Nem ismert konstrukció olyan 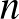 csúcsú gráfra, amiben minden klikk és független halmaz mérete polinomiális lenne
csúcsú gráfra, amiben minden klikk és független halmaz mérete polinomiális lenne 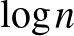 -ben. Ennek ellenére tudjuk, hogy a Ramsey-tételben szereplő
-ben. Ennek ellenére tudjuk, hogy a Ramsey-tételben szereplő 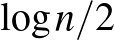 körüli korlát majdnem éles, mert majdnem minden
körüli korlát majdnem éles, mert majdnem minden 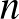 -csúcsú gráfra igaz, hogy nincs benne sem
-csúcsú gráfra igaz, hogy nincs benne sem  csúcsú klikk, sem ekkora független halmaz. Ennek belátásához elég észrevennünk, hogy egy
csúcsú klikk, sem ekkora független halmaz. Ennek belátásához elég észrevennünk, hogy egy 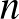 csúcsú gráfot tekinthetünk a csúcspárok kétszínezésének: ha van él a két csúcs között, az jelenti az egyik színt, ha nincs él, az a másikat. Ebben a megfogalmazásban egy
csúcsú gráfot tekinthetünk a csúcspárok kétszínezésének: ha van él a két csúcs között, az jelenti az egyik színt, ha nincs él, az a másikat. Ebben a megfogalmazásban egy  csúcshalmaz klikk vagy független halmaz, ha az
csúcshalmaz klikk vagy független halmaz, ha az  -beli párok alkotta
-beli párok alkotta 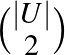 méretű halmaz egyszínű. Annak eldöntése tehát, hogy van-e
méretű halmaz egyszínű. Annak eldöntése tehát, hogy van-e 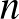 csúcsú gráf
csúcsú gráf 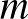 méretű klikk vagy független halmaz nélkül, épp egy hipergráf kétszínezési probléma. Ez egy
méretű klikk vagy független halmaz nélkül, épp egy hipergráf kétszínezési probléma. Ez egy  -uniform hipergráf, amiben
-uniform hipergráf, amiben  hiperél van, ezek az
hiperél van, ezek az 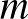 méretű csúcshalmazoknak felelnek meg. A fent bizonyított eredmény szerint tehát van
méretű csúcshalmazoknak felelnek meg. A fent bizonyított eredmény szerint tehát van 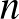 csúcsú gráf, amiben nincs
csúcsú gráf, amiben nincs 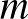 elemű klikk vagy független halmaz, ha
elemű klikk vagy független halmaz, ha 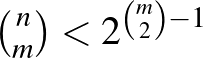 . Egyszerű számítás mutatja, hogy
. Egyszerű számítás mutatja, hogy 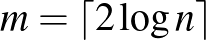 választás mellett (
választás mellett (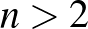 esetén) teljesül a feltétel, tehát a Ramsey tételében szereplő korlát nagyságrendileg éles. (Sőt, azt sem nehéz megmutatni, hogy ahogy
esetén) teljesül a feltétel, tehát a Ramsey tételében szereplő korlát nagyságrendileg éles. (Sőt, azt sem nehéz megmutatni, hogy ahogy  nő, az ilyen, úgynevezett Ramsey-gráfok aránya az összes
nő, az ilyen, úgynevezett Ramsey-gráfok aránya az összes 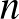 csúcsú gráf között 1-hez tart.) Ezt az alsó becslést Erdős Pál látta be 1947-ben, [1], de az alsó és felső becslés közötti négyes faktort azóta sem sikerült lejjebb szorítani.
csúcsú gráf között 1-hez tart.) Ezt az alsó becslést Erdős Pál látta be 1947-ben, [1], de az alsó és felső becslés közötti négyes faktort azóta sem sikerült lejjebb szorítani.
Lovász lokális lemmája Erdős és Lovász egy 1975-ös cikkében jelent meg, [2]. Ők is a hipergráf kétszínezési problémát vizsgálták. Azt bizonyították, hogy egy 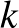 -uniform hipergráf kétszínezhető, ha
-uniform hipergráf kétszínezhető, ha 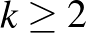 és tetszőleges
és tetszőleges 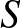 hiperélet maximum
hiperélet maximum  másik hiperél metsz. A fenti egyszerű gondolatmenet akkor adta a kétszínezhetőséget, ha a hiperélek teljes száma kevesebb, mint
másik hiperél metsz. A fenti egyszerű gondolatmenet akkor adta a kétszínezhetőséget, ha a hiperélek teljes száma kevesebb, mint 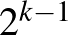 , tehát egy globális korlátot adott a hipergráf méretére. Az Erdős-Lovász eredmény numerikus korlátja icipicit gyengébb, de az egy lokális korlát. A teljes hipergráf mérete tetszőleges (akár végtlelen is) lehet, csak az a lényeg, hogy egyetlen hiperél hány másikat metsz. Ez lehetővé tette a véletlen módszer alkalmazását a korábbinál sokkal több esetben. Míg korábban a véletlen módszert főleg olyankor lehetett alkalmazni, ha egy véletlenül választott struktúra (gráf, színezés, stb.) nagy eséllyel teljesítette a kivánalmakat, az új módszer, amely a Lovász-féle lokális lemma alkalmazásán alapul, sok olyan esetben is működik, amikor „tűt keresünk a szénakazalban”, azaz annak a valószínűsége, hogy egy véletlen struktúra megfelel, akár exponenciálisan kicsi is lehet. Ilyen a hipergráf kétszínezés is: ahogy a hipergráf mérete nő, a véletlen színezés egyre nagyobb valószínűséggel teszi egyszínűvé valamelyik élet.
, tehát egy globális korlátot adott a hipergráf méretére. Az Erdős-Lovász eredmény numerikus korlátja icipicit gyengébb, de az egy lokális korlát. A teljes hipergráf mérete tetszőleges (akár végtlelen is) lehet, csak az a lényeg, hogy egyetlen hiperél hány másikat metsz. Ez lehetővé tette a véletlen módszer alkalmazását a korábbinál sokkal több esetben. Míg korábban a véletlen módszert főleg olyankor lehetett alkalmazni, ha egy véletlenül választott struktúra (gráf, színezés, stb.) nagy eséllyel teljesítette a kivánalmakat, az új módszer, amely a Lovász-féle lokális lemma alkalmazásán alapul, sok olyan esetben is működik, amikor „tűt keresünk a szénakazalban”, azaz annak a valószínűsége, hogy egy véletlen struktúra megfelel, akár exponenciálisan kicsi is lehet. Ilyen a hipergráf kétszínezés is: ahogy a hipergráf mérete nő, a véletlen színezés egyre nagyobb valószínűséggel teszi egyszínűvé valamelyik élet.
A fenti hipergráf kétszínezési eredmény egyszerűen következik a lokális lemma alábbi, egyik legegyszerűbb formájából. A továbbiakban 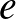 a természetes alapú logaritmus alapja,
a természetes alapú logaritmus alapja, 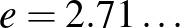
Lovász lokális lemma (szimmetrikus változat). Legyen  események egy véges családja egy valószínűségi térben, ezeket hívjuk rossz eseményeknek. Tegyük fel továbbá, hogy adott egy
események egy véges családja egy valószínűségi térben, ezeket hívjuk rossz eseményeknek. Tegyük fel továbbá, hogy adott egy 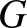 gráf (a függőségi gráf), amelynek csúcsai a rossz események, és teljesül, hogy tetszőleges
gráf (a függőségi gráf), amelynek csúcsai a rossz események, és teljesül, hogy tetszőleges  rossz esemény független a vele nem szomszédos rossz események halmazától. Legyen
rossz esemény független a vele nem szomszédos rossz események halmazától. Legyen 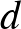 a
a 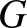 gráf maximális foka. Ha egyetlen rossz esemény valószínűsége sem több, mint
gráf maximális foka. Ha egyetlen rossz esemény valószínűsége sem több, mint 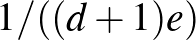 , akkor pozitív annak a valószínűsége, hogy egyik rossz esemény sem következik be.
, akkor pozitív annak a valószínűsége, hogy egyik rossz esemény sem következik be.
A lemmában egyetlen bonyolult fogalom szerepel, ez a függetlenség. Az  és a
és a  eseményt függetlennek mondjuk, ha
eseményt függetlennek mondjuk, ha ![$P\left[A\wedge B\right]=P[A]P[B]$](/images/stories/latexuj/2021-06/2021-06-lovaszlocallemma/img34.png) . Itt
. Itt 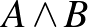 az
az  és
és  események metszetét jelöli, tehát azt, hogy mindkettő bekövetkezik. Például két diszjunkt halmaz egyszínűsége egy uniform véletlen színezésben független. A lemmában azonban nem páronkénti függetlenség szerepel, hanem ennél valamivel több. Azt mondjuk, hogy az
események metszetét jelöli, tehát azt, hogy mindkettő bekövetkezik. Például két diszjunkt halmaz egyszínűsége egy uniform véletlen színezésben független. A lemmában azonban nem páronkénti függetlenség szerepel, hanem ennél valamivel több. Azt mondjuk, hogy az  esemény független események egy
esemény független események egy 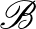 halmazától, ha
halmazától, ha  minden olyan
minden olyan  eseménytől független, ami a
eseménytől független, ami a 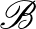 -beli események kombinációjaként leírható, tehát ahol
-beli események kombinációjaként leírható, tehát ahol  megadható azzal, hogy kikötjük néhány
megadható azzal, hogy kikötjük néhány 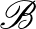 -beli eseményről, hogy teljesüljön, míg más
-beli eseményről, hogy teljesüljön, míg más 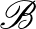 -beliekről, hogy ne teljesüljenek. (Nem nehéz belátni, hogy ekvivalens definíciót kapunk, ha csak az egyik típusú kikötést engedjük meg. A lemma bizonyításában is csak azt fogjuk használni, hogy a megfelelő
-beliekről, hogy ne teljesüljenek. (Nem nehéz belátni, hogy ekvivalens definíciót kapunk, ha csak az egyik típusú kikötést engedjük meg. A lemma bizonyításában is csak azt fogjuk használni, hogy a megfelelő  esemény független az olyan
esemény független az olyan  eseményektől, amik bizonyos
eseményektől, amik bizonyos 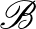 -beliek nem-teljesülésével adhatók meg.)
-beliek nem-teljesülésével adhatók meg.)
Nézzük meg hogyan következik a fent említett eredmény 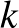 -uniform hipergráfok kétszínezéséről a lokális lemmából. Az alaphalmaz uniform véletlen kétszínezését vizsgáljuk. A rossz események a hiperélekhez tartoznak: azt tekintjük rossznak, ha a hiperél egyszínű. Mindegyik rossz esemény valószínűsége
-uniform hipergráfok kétszínezéséről a lokális lemmából. Az alaphalmaz uniform véletlen kétszínezését vizsgáljuk. A rossz események a hiperélekhez tartoznak: azt tekintjük rossznak, ha a hiperél egyszínű. Mindegyik rossz esemény valószínűsége  . A
. A 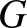 függetlenségi gráfban két rossz eseményt összekötünk, ha a hozzájuk tartozó hiperélek metszik egymást. A lemma függetlenségi feltétele teljesül, hiszen ha az
függetlenségi gráfban két rossz eseményt összekötünk, ha a hozzájuk tartozó hiperélek metszik egymást. A lemma függetlenségi feltétele teljesül, hiszen ha az  rossz esemény egy
rossz esemény egy 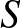 hiperél egyszínűsége, akkor
hiperél egyszínűsége, akkor  csak az
csak az 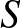 -ben szereplő pontok színétől függ, míg az
-ben szereplő pontok színétől függ, míg az  -val nem szomszédos rossz események (és így azok kombinációi is) csak az
-val nem szomszédos rossz események (és így azok kombinációi is) csak az 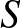 -en kívüli elemek színétől függenek, így függetlenek
-en kívüli elemek színétől függenek, így függetlenek  -tól. Ha most a
-tól. Ha most a 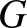 gráf
gráf 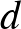 maximális fokszámára
maximális fokszámára 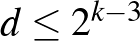 , és
, és 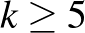 , akkor teljesül
, akkor teljesül 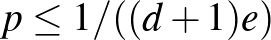 , tehát a lemma szerint pozitív eséllyel az összes rossz esemény elkerülhető, ami épp a hipergráf kétszínezhetőségét jelenti. (A
, tehát a lemma szerint pozitív eséllyel az összes rossz esemény elkerülhető, ami épp a hipergráf kétszínezhetőségét jelenti. (A 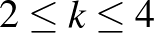 eset nagyon egyszerűen adódik direkt meggondolásból, de a lokális lemma egy másik formáját is használhatjuk.) Ez a gondolatmenet csak véges hipergráfokra alkalmazható, a végtelen eset ebből kompaktsági meggondolásokkal következik.
eset nagyon egyszerűen adódik direkt meggondolásból, de a lokális lemma egy másik formáját is használhatjuk.) Ez a gondolatmenet csak véges hipergráfokra alkalmazható, a végtelen eset ebből kompaktsági meggondolásokkal következik.
Sokkal egyszerűbb lenne a lokális lemma kimondása, ha csak páronkénti függetlenséget használnánk benne. A függőségi gráfot ekkor egyszerűen úgy definiálhatnánk, hogy két rossz esemény között akkor van él, ha nem függetlenek. Sajnos a lokális lemma így kapott erősebb változata nem igaz. Ezt könnyen láthatjuk pont a hipergráf kétszínezési feladatból. Két hiperél egyszínűsége nem csak akkor független, ha hiperélek diszjunktak, hanem akkor is, ha egyetlen elemben metszik egymást. Így ha a hipergráfunk egyszerű, azaz bármely két hiperél legfeljebb egy pontban metszi egymást, akkor a függőségi gráf üres lenne, maximális fokszáma pedig 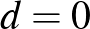 . Ismert azonban, hogy tetszőleges
. Ismert azonban, hogy tetszőleges 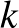 -ra létezik nem kétszínezhető
-ra létezik nem kétszínezhető 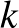 -uniform egyszerű hipergráf. Egy ilyen 3-uniform hipergráfot adnak például a Fano-sík egyenesei, és már ez is mutatja, hogy a lokális lemmának ez az erősebb verziója nem lehet igaz.
-uniform egyszerű hipergráf. Egy ilyen 3-uniform hipergráfot adnak például a Fano-sík egyenesei, és már ez is mutatja, hogy a lokális lemmának ez az erősebb verziója nem lehet igaz.
A lokális lemmának azonban sok más erősebb formája ismert. Shearer, [3] pontosan meghatározta, hogy adott 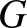 függőségi gráf és a rossz események adott valószínűsége mellett mikor következtethetünk arra, hogy az összes rossz eseményt pozitív valószínűséggel elkerüljük. Itt most csak egy ennél kevésbé általános, de egyszerűbb verziót idézünk, ami azonban még így is jóval általánosabb a fenti szimmetrikus változatnál. Vegyük észre, hogy ez a változat mindig alkalmazható, amikor a szimmetrikus változat, de néha olyankor is, amikor az nem.
függőségi gráf és a rossz események adott valószínűsége mellett mikor következtethetünk arra, hogy az összes rossz eseményt pozitív valószínűséggel elkerüljük. Itt most csak egy ennél kevésbé általános, de egyszerűbb verziót idézünk, ami azonban még így is jóval általánosabb a fenti szimmetrikus változatnál. Vegyük észre, hogy ez a változat mindig alkalmazható, amikor a szimmetrikus változat, de néha olyankor is, amikor az nem.
Lovász lokális lemma (egy aszimmetrikus változat) Legyen  „rossz” események egy véges családja, legyen
„rossz” események egy véges családja, legyen 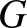 egy gráf ezeken az eseményeken, mint csúcsokon, és tegyük fel, hogy minden rossz esemény független a vele nem szomszédos rossz események halmazától. Ha minden
egy gráf ezeken az eseményeken, mint csúcsokon, és tegyük fel, hogy minden rossz esemény független a vele nem szomszédos rossz események halmazától. Ha minden 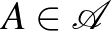 rossz eseményre teljesül, hogy
rossz eseményre teljesül, hogy ![$P[A]+\sum_{B\sim A}P[B]<1/e$](/images/stories/latexuj/2021-06/2021-06-lovaszlocallemma/img45.png) , ahol
, ahol  szomszédaira összegzünk, akkor pozitív annak a valószínűsége, hogy egyik rossz esemény sem következik be.
szomszédaira összegzünk, akkor pozitív annak a valószínűsége, hogy egyik rossz esemény sem következik be.
A lokális lemma bizonyítása
A cikket a lokális lemma szimmetrikus változatának bizonyításával zárom. Néha átütő erejű eredményeknek is nagyon egyszerű a bizonyítása, csak éppen megtalálni nehéz ezt az (utólag) egyszerű bizonyítást. Ez is egy ilyen eset. A bizonyítás megtalálásának körülményeiről is mesél Lovász egy nemrégi Telex-interjúban.
Bevezetünk néhány egyszerű jelölést: 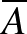 az
az  esemény komplementerét jelöli, azaz
esemény komplementerét jelöli, azaz 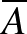 akkor teljesül, ha
akkor teljesül, ha  nem. Két esemény metszetéhez hasonlóan, a
nem. Két esemény metszetéhez hasonlóan, a  jelet használjuk akárhány esemény metszetére:
jelet használjuk akárhány esemény metszetére: 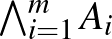 tehát akkor teljesül, ha valamennyi
tehát akkor teljesül, ha valamennyi  teljesül. Előfordul, hogy nulla esemény metszetéről fogunk beszélni, ez a teljes esemény, ami mindig teljesül. A bizonyítás kulcsfogalma a feltételes valószínűség. Ha
teljesül. Előfordul, hogy nulla esemény metszetéről fogunk beszélni, ez a teljes esemény, ami mindig teljesül. A bizonyítás kulcsfogalma a feltételes valószínűség. Ha  és
és  események,
események, ![$P[B]>0$](/images/stories/latexuj/2021-06/2021-06-lovaszlocallemma/img50.png) , akkor
, akkor  valószínűsége, feltéve
valószínűsége, feltéve  definíciója:
definíciója: ![$P\left[A\vert B\right]=P\left[A\wedge B\right]/P[B]$](/images/stories/latexuj/2021-06/2021-06-lovaszlocallemma/img51.png) . Használni fogjuk a feltételes valószínűség néhány egyszerű tulajdonságát, mint
. Használni fogjuk a feltételes valószínűség néhány egyszerű tulajdonságát, mint ![$P\left[\overline A\vert B\right]=1-P\left[A\vert B\right]$](/images/stories/latexuj/2021-06/2021-06-lovaszlocallemma/img52.png) , vagy a láncszabály:
, vagy a láncszabály: ![$P\left[A\wedge B\vert C\right]=P\left[B\vert C\right]P\left[A\vert B\wedge C\right]$](/images/stories/latexuj/2021-06/2021-06-lovaszlocallemma/img53.png) . Ezek egyszerűen levezethetőek a definíció behelyettesítésével.
. Ezek egyszerűen levezethetőek a definíció behelyettesítésével.
A kulcs a következő lemma igazolása. Észrevehetjük, hogy a lokális lemmában szereplő 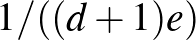 korlát helyett a valamivel nagyobb
korlát helyett a valamivel nagyobb 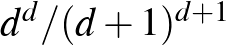 korlát is elegendő lenne a bizonyításhoz.
korlát is elegendő lenne a bizonyításhoz.
Lemma A szimmetrikus lokális lemma feltételei mellett minden  és tőle különböző
és tőle különböző  rossz eseményre teljesül, hogy
rossz eseményre teljesül, hogy ![$P\left[A\vert\bigwedge_{i=1}^m\overline B_i\right]<1/(d+1)$](/images/stories/latexuj/2021-06/2021-06-lovaszlocallemma/img56.png) .
.
Bizonyítás. Az állítást 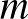 -re vonatkozó indukcióval bizonyítjuk. Az
-re vonatkozó indukcióval bizonyítjuk. Az 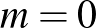 alapeset egyszerűen kezelhető, de tekinthető az általános induktív lépés speciális esetének is. Tegyük tehát fel, hogy az állítás teljesül
alapeset egyszerűen kezelhető, de tekinthető az általános induktív lépés speciális esetének is. Tegyük tehát fel, hogy az állítás teljesül 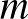 kisebb értékeire, és igazoljuk a lemmában szereplő egyenlőtlenséget. Feltehetjük, hogy a
kisebb értékeire, és igazoljuk a lemmában szereplő egyenlőtlenséget. Feltehetjük, hogy a  események között előbb szerepelnek azok, amelyek a függőségi gráfban
események között előbb szerepelnek azok, amelyek a függőségi gráfban  szomszédai, mint azok, amelyek nem. Tehát
szomszédai, mint azok, amelyek nem. Tehát 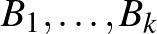 szomszédja
szomszédja  -nak,
-nak,  nem. A láncszabály ismételt alkalmazásával ezt kapjuk:
nem. A láncszabály ismételt alkalmazásával ezt kapjuk:
![$\displaystyle P\left[A\wedge\bigwedge_{i=1}^k\overline B_i\,\Big\vert\bigwedge_...
...{i=1}^kP\left[\overline B_i\,\Big\vert\bigwedge_{j=i+1}^m\overline B_j\right].
$](/images/stories/latexuj/2021-06/2021-06-lovaszlocallemma/img61.png)
A képlet jobb oldalán megjelenik a becsülendő mennyiség, a képletben megjelenő többi feltételes valószínűséget meg egyenként megbecsüljük. Az induktív feltevésünk miatt teljesül, hogy
![$\displaystyle P\left[\overline B_i\,\Big\vert\bigwedge_{j=i+1}^m\overline B_j\r...
...\Big\vert\bigwedge_{j=i+1}^m\overline B_j\right]\ge1-\frac1{d+1}=\frac d{d+1},
$](/images/stories/latexuj/2021-06/2021-06-lovaszlocallemma/img62.png)
hiszen a feltétel itt már 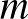 -nél kevesebb
-nél kevesebb 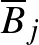 metszete. Tudjuk, hogy
metszete. Tudjuk, hogy  független a
független a  eseményektől, valamint hogy
eseményektől, valamint hogy ![$P\left[A\vert C\right]=P[A]$](/images/stories/latexuj/2021-06/2021-06-lovaszlocallemma/img64.png) teljesül, ha
teljesül, ha  és
és  független, így:
független, így:
![$\displaystyle P\left[A\wedge\bigwedge_{i=1}^k\overline B_i\,\Big\vert\bigwedge_...
...B_j\right]\le P\left[A\,\Big\vert\bigwedge_{j=k+1}^n\overline B_j\right]=P[A].
$](/images/stories/latexuj/2021-06/2021-06-lovaszlocallemma/img65.png)
A fenti három képletet összerakva:
![$\displaystyle P\left[A\,\Big\vert\bigwedge_{j=1}^m\overline B_j\right]=\frac{P\...
...e B_i\vert\bigwedge_{j=i+1}^m\overline B_j\right]}\le\frac{P[A]}{(d/(d+1))^k}.
$](/images/stories/latexuj/2021-06/2021-06-lovaszlocallemma/img66.png)
Ezzel lényegében meg is vagyunk, hiszen 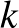 legfeljebb
legfeljebb  fokszáma a függőségi gráfban, tehát legfeljebb
fokszáma a függőségi gráfban, tehát legfeljebb 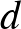 ,
, ![$P[A]$](/images/stories/latexuj/2021-06/2021-06-lovaszlocallemma/img67.png) pedig becsülhető
pedig becsülhető 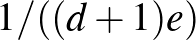 -vel. Végezetül felhasználjuk a közismert
-vel. Végezetül felhasználjuk a közismert  egyenlőtlenséget, és ezzel a lemma bizonyítást nyert:
egyenlőtlenséget, és ezzel a lemma bizonyítást nyert:
![$\displaystyle P\left[A\,\Big\vert\bigwedge_{j=1}^m\overline B_j\right]\le\frac{...
...+1)e)}{(d/(d+1))^d}=\frac1{d+1}\cdot\frac{(1+1/d)^d}e<\frac1{d+1}.\quad\square
$](/images/stories/latexuj/2021-06/2021-06-lovaszlocallemma/img69.png)
A fenti lemmából gyorsan levezethető a lokális lemma állítása. Legyen 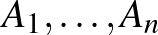 az összes rossz esemény felsorolása. Megint a láncszabályt alkalmazzuk ismételten:
az összes rossz esemény felsorolása. Megint a láncszabályt alkalmazzuk ismételten:
![$\displaystyle P\left[\bigwedge_{i=1}^n\overline A_i\right]=\prod_{i=1}^nP\left[...
...bigwedge_{j=i+1}^n\overline A_j\right]\right)>\left(\frac d{d+1}\right)^n\ge0.
$](/images/stories/latexuj/2021-06/2021-06-lovaszlocallemma/img71.png)
Köszönet
Hálás vagyok Simonyi Gábornak a cikk megírásában nyújtott segítségért.
Irodalomjegyzék
- [1] P. Erdős, Some remarks on the theory of graphs, Bull. Amer. Math. Soc.53 (4) (1947), 292–294.
[2] P. Erdős, L. Lovász, Problems and results on 3-chromatic hypergraphs and some related questions, in: Infinite and Finite Sets II (A. Hajnal, R. Rado, V. T. Sós, eds.) North-Holland (1975), pp. 609–627.
[3] J. B. Shearer, On a problem of Spencer, Combinatorica 5 (3) (1985), 241–245.
Tardos Gábor
Rényi Alfréd Matematikai Kutatóintézet









