1. Bevezető
Lovász László 2021-ben megkapott Abel-díja jó alkalmat szolgáltat arra, hogy áttekintést adjunk híresebb eredményeiről. Ebben a cikkben az egyik első világraszóló eredményéről, a perfekt gráf sejtésről lesz szó.
Lovász László 50 évvel ezelőtt, 1971-ben bizonyította és 1972-ben megjelent cikkében publikálta bizonyítását a perfekt gráf sejtésre [15], amely így azóta Lovász tétel vagy perfekt gráf tétel. Továbbá egy szintén 1972-ben megjelent másik dolgozatában [16] megadta a perfekt gráfoknak egy olyan karakterizációját, amelyből szintén következett a perfekt gráf sejtés bizonyítása. Az eredmény és a bizonyítások egyből a kombinatorikai alapműveltség részévé lettek, azóta is lényegében minden gráfelméleti alapozó kurzus kimaradhatatlan részei. Ha hatásukat számokkal szeretnénk jellemezni, akkor talán a két cikk idézettsége a megfelelő mutatószám: [15]-re 928, míg [16]-ra 477 idézőt számol a Google Scholar így 2021. május végén.
A továbbiakban egy rövid, bevezető jellegű írást közlünk a tételről, ami remélhetőleg komolyabb kombinatorikai tudás nélkül is követhető lesz, legalább a nagy kép tekintetében. Először a tétel állításával ismerkedünk meg, majd arról mondunk pár szót, és hogy mi motiválta a perfekt gráf fogalmát és magát a sejtést (hogyan kapcsolódik a téma a korábbi eredményekhez), végül a bizonyításról és néhány azóta született eredményről lesz szó.
Ahhoz, hogy magát a perfekt gráf tételt ki tudjuk mondani, előbb pár fogalmat be kell vezetnünk. Egy (egyszerű, irányítatlan)  gráf egy
gráf egy 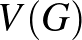 csúcshalmazból és egy
csúcshalmazból és egy  élhalmazból áll, ahol az élek csúcspároknak felelnek meg, tehát az élhalmaz az összes csúcspárok halmazának egy részhalmaza. Egy
élhalmazból áll, ahol az élek csúcspároknak felelnek meg, tehát az élhalmaz az összes csúcspárok halmazának egy részhalmaza. Egy  gráf
gráf 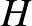 részgráfján olyan
részgráfján olyan 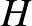 gráfot értünk, melyre igaz, hogy
gráfot értünk, melyre igaz, hogy 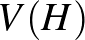 részhalmaza
részhalmaza 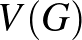 -nek és
-nek és  részhalmaza
részhalmaza  -nek.
-nek.  egy
egy 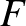 feszített részgráfján
feszített részgráfján  -nek olyan
-nek olyan 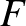 részgráfját értjük, amelyre igaz, hogy
részgráfját értjük, amelyre igaz, hogy 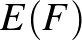 pontosan a
pontosan a 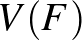 csúcsai közt menő
csúcsai közt menő  -beli élekből áll (tehát az összes olyan él halmaza, amelyet
-beli élekből áll (tehát az összes olyan él halmaza, amelyet 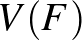 -beli pontok
-beli pontok  -ben „kifeszítenek”)1.
-ben „kifeszítenek”)1.
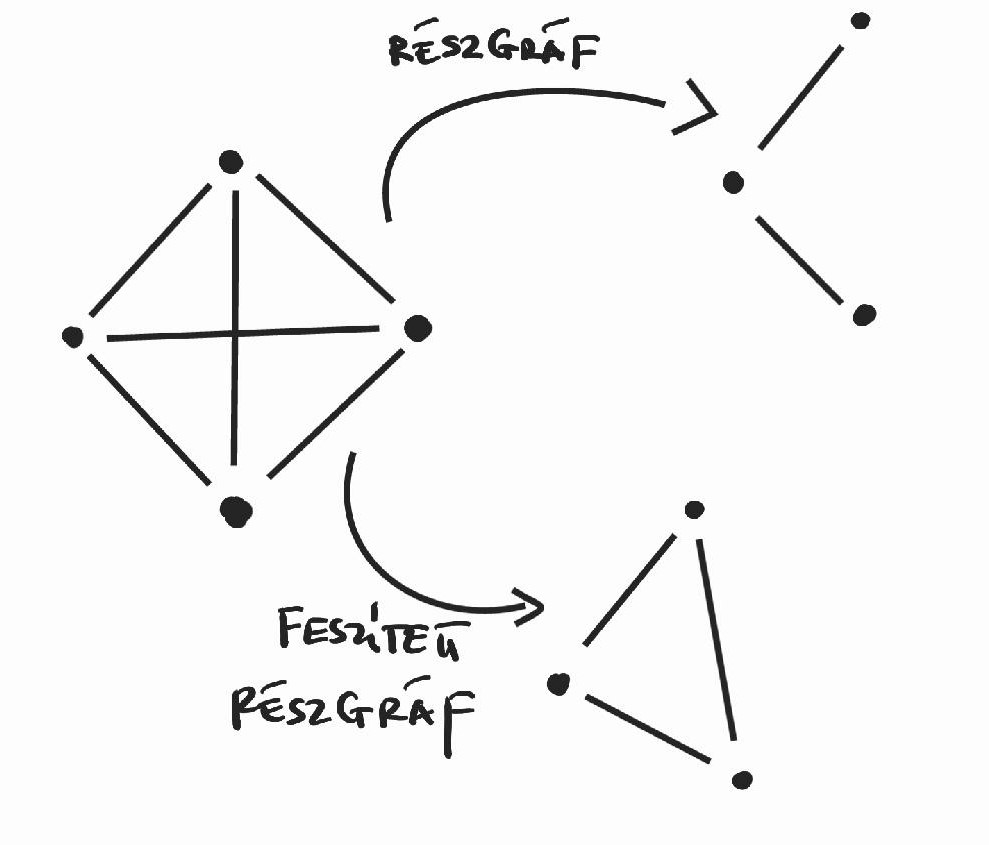
1. ábra. Egy 4-csúcsú gráf részgráfja és feszített részgráfja
Egy  gráf komplementerén azt a
gráf komplementerén azt a 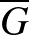 gráfot értjük, amelyre igaz, hogy a csúcshalmaza ugyanúgy
gráfot értjük, amelyre igaz, hogy a csúcshalmaza ugyanúgy 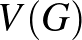 , mint
, mint  -nek, de
-nek, de 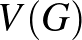 csúcspárjaiból pontosan azokat tesszük bele az élhalmazba, amiket
csúcspárjaiból pontosan azokat tesszük bele az élhalmazba, amiket  ‑be nem (azaz, ha valami él volt
‑be nem (azaz, ha valami él volt  -ben, most nem lesz az és ha nem volt az, most az lesz).
-ben, most nem lesz az és ha nem volt az, most az lesz).

2. ábra. Egy gráf és komplementere
A 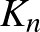 -nel jelölt
-nel jelölt 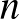 csúcsú teljes gráfon azt a gráfot értjük, amelyben bármely két különböző csúcs élt alkot. Egy adott
csúcsú teljes gráfon azt a gráfot értjük, amelyben bármely két különböző csúcs élt alkot. Egy adott  gráf esetén azt a legnagyobb
gráf esetén azt a legnagyobb 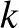 számot, amelyre
számot, amelyre  -nek van
-nek van 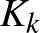 (-val izomorf2) részgráfja,
(-val izomorf2) részgráfja,  klikkszámának mondjuk és
klikkszámának mondjuk és 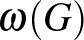 -vel jelöljük. Tehát pl. az 1. ábra (bal oldalán) látható gráfot felismerhetjük:
-vel jelöljük. Tehát pl. az 1. ábra (bal oldalán) látható gráfot felismerhetjük: 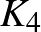 , aminek a klikkszáma,
, aminek a klikkszáma,  .
.
A  gráfban egy független csúcshalmaz3 egy olyan
gráfban egy független csúcshalmaz3 egy olyan  részhalmaza
részhalmaza 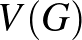 -nek, amelyre igaz, hogy
-nek, amelyre igaz, hogy  -beli csúcsok közt nincsenek élek
-beli csúcsok közt nincsenek élek  -ben. A legnagyobb olyan
-ben. A legnagyobb olyan 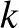 számot, amelyre igaz, hogy van
számot, amelyre igaz, hogy van  -ben
-ben 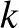 csúcsot tartalmazó független halmaz,
csúcsot tartalmazó független halmaz,  függetlenségi számának nevezzük és
függetlenségi számának nevezzük és  -vel jelöljük. Ha már bevezettünk pár fogalmat, akkor most pihenésképp kicsit gyakoroljunk, próbáljuk meg őket összekapcsolni és gondoljuk végig, hogy
-vel jelöljük. Ha már bevezettünk pár fogalmat, akkor most pihenésképp kicsit gyakoroljunk, próbáljuk meg őket összekapcsolni és gondoljuk végig, hogy  a legnagyobb olyan
a legnagyobb olyan 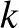 szám, amelyre
szám, amelyre 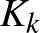 részgráfja
részgráfja 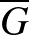 -nek, tehát
-nek, tehát 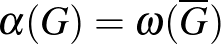 .
.
Az utolsó fogalom, amire a perfekt gráf tétel kimondása előtt szükségünk van, a kromatikus szám. Egy 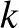 pozitív egész számra a
pozitív egész számra a  gráf csúcsainak egy jó
gráf csúcsainak egy jó 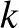 -színezésén azt értjük, hogy kiszínezzük a csúcsait legfeljebb
-színezésén azt értjük, hogy kiszínezzük a csúcsait legfeljebb 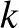 színnel, méghozzá úgy, hogy éllel összekötött csúcsok különböző színeket kapjanak. (Az alábbi ábrán egy gráf 3 színnel való jó színezését látjuk.) Azt a legkisebb
színnel, méghozzá úgy, hogy éllel összekötött csúcsok különböző színeket kapjanak. (Az alábbi ábrán egy gráf 3 színnel való jó színezését látjuk.) Azt a legkisebb 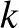 pozitív egész számot, amire a
pozitív egész számot, amire a  gráfnak van jó
gráfnak van jó 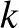 -színezése, a gráf kromatikus számának nevezzük és
-színezése, a gráf kromatikus számának nevezzük és 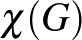 -vel jelöljük.
-vel jelöljük.
Egy színezésnél az azonos színt kapott csúcsok halmazát színosztály(ok)nak mondjuk. Hogy a kromatikus számot is összekössük az előző fogalmakkal, vegyük észre, hogy minden színosztály független csúcshalmazt alkot (a színezési szabály szerint nem lehet él két azonos színű csúcs közt), tehát egy gráf jó  -színezése ugyanazt jelenti, mint csúcsainak
-színezése ugyanazt jelenti, mint csúcsainak 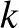 független csúcshalmazba való osztása.
független csúcshalmazba való osztása.
3. ábra. Egy 4-pontú gráf jó színezése 3 színnel
Ugyan a fogalmak bevezetésén túl vagyunk, de a tétel kimondása előtt még próbáljuk meg összehasonlítani a két mennyiséget: 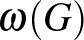 -t és
-t és 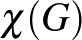 -t. Amire kis gondolkodással rájöhetünk, hogy
-t. Amire kis gondolkodással rájöhetünk, hogy  fennáll, hiszen egy
fennáll, hiszen egy 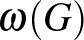 csúcsszámú teljes részgráfban bármely két (különböző) csúcsot különböző színekkel kell színezni, ami így ad egy alsó becslést
csúcsszámú teljes részgráfban bármely két (különböző) csúcsot különböző színekkel kell színezni, ami így ad egy alsó becslést 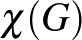 -re. 4
-re. 4
Ennyi előkészület után bevezetjük a perfekt gráf fogalmát, amelyet Claude Berge5 egy 1960 áprilisában Halle-Wittenbergben megtartott gráfelméleti konferencia konferenciakötetében [1] definiált először. Egy  gráfot perfektnek mondunk, ha minden feszített
gráfot perfektnek mondunk, ha minden feszített 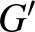 részgráfjára (így például az egész
részgráfjára (így például az egész  gráfra is) igaz, hogy
gráfra is) igaz, hogy 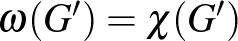 . Tehát kissé pongyolán úgy fogalmazhatunk, hogy
. Tehát kissé pongyolán úgy fogalmazhatunk, hogy  bármely feszített részgráfjának a kromatikus számát csak a legnagyobb klikk mérete befolyásolja, a színezésnél nincsenek további plusz „akadályok”. A fogalom további motivációiról kicsit később lesz szó.
bármely feszített részgráfjának a kromatikus számát csak a legnagyobb klikk mérete befolyásolja, a színezésnél nincsenek további plusz „akadályok”. A fogalom további motivációiról kicsit később lesz szó.
Az olvasó könnyen beláthatja, hogy a teljes gráfok vagy például a teljes gráfok komplementerei az ún. üres gráfok perfektek. Ugyanakkor könnyű mutatni olyan gráfcsaládot is, amelynek tagjai nem perfektek. Egy 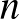 hosszú körön azt a
hosszú körön azt a 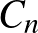 gráfot értjük, amelynek csúcshalmaza
gráfot értjük, amelynek csúcshalmaza 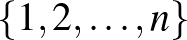 , az élhalmaza pedig
, az élhalmaza pedig 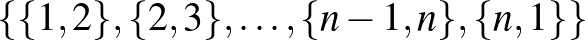 . A 2. ábra bal oldalán lévő
. A 2. ábra bal oldalán lévő  gráf például egy
gráf például egy  . Talán nem látszik elsőre, de gondoljuk meg, hogy a mellette lévő
. Talán nem látszik elsőre, de gondoljuk meg, hogy a mellette lévő  is egy
is egy 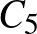 . Ha
. Ha 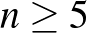 páratlan egész, akkor
páratlan egész, akkor 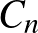 nem perfekt gráf, hiszen a legnagyobb klikk mérete 2, míg a kromatikus száma 3. Amiből az is következik, hogy ha egy
nem perfekt gráf, hiszen a legnagyobb klikk mérete 2, míg a kromatikus száma 3. Amiből az is következik, hogy ha egy  gráf tartalmaz feszített részgráfként egy páratlan kört6, akkor nem lehet perfekt. Ugyanígy könnyen belátható, hogy egy legalább 5 hosszú páratlan kör komplementere sem perfekt. (Ennek belátása jó gyakorló feladat lehet az olvasónak.)
gráf tartalmaz feszített részgráfként egy páratlan kört6, akkor nem lehet perfekt. Ugyanígy könnyen belátható, hogy egy legalább 5 hosszú páratlan kör komplementere sem perfekt. (Ennek belátása jó gyakorló feladat lehet az olvasónak.)
Berge perfekt gráfokkal kapcsolatban az alább látható sejtéseket fogalmazta meg [2]. A perfekt gráf sejtés motivációjáról kicsit később lesz szó, de az erős perfekt gráf sejtés mögött álló gondolat már most nagyjából érthető: Berge azt vélte, hogy pontosan a (legalább 5 hosszú) páratlan körök és komplementereik, mint feszített részgráfok okoznak problémát a perfektség szempontjából. Tehát kizárt feszített részgráfok segítségével akarta karakterizálni a perfektséget.
Perfekt gráf sejtés (Berge, 1963). Egy gráf pontosan akkor perfekt, ha a komplementere is az.
Erős perfekt gráf sejtés (Berge, 1963). Egy gráf pontosan akkor perfekt, ha nem tartalmaz feszített részgráfként sem legalább 5 hosszú páratlan kört, sem legalább 5 hosszú páratlan kör komplementerét.
Lovász László a perfekt gráf sejtést bizonyította 1972-ben megjelent cikkében [15], amit mondjunk ki újra immár tételként:
Perfekt gráf tétel (Lovász, 1972 7) Egy gráf pontosan akkor perfekt, ha a komplementere perfekt.
Egy másik, szintén 1972-ben megjelent dolgozatában [16] (Hajnal András javaslatára) egy tetszetős karakterizációját adta a perfektségnek, melynek következménye a perfekt gráf tétel.
Tétel (Lovász, 1972). Egy  gráf pontosan akkor perfekt, ha
gráf pontosan akkor perfekt, ha
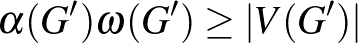
teljesül minden 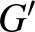 feszített részgráfjára.
feszített részgráfjára.
Ez utóbbi tételnek könnyen láthatóan következménye a perfekt gráf tétel a „komplementer alak” miatt.
2. Előzmények, motiváció
Ebben a fejezetben arról lesz szó, hogy milyen korábbi eredmények motiválták Berge-t, milyen utak mentén lehet magáig a perfekt gráf fogalmáig és a sejtésig eljutni.
2.1. A „magyarabb” út
Berge számára jelentős insipirációt jelentettek egyes páros gárfokra vonatkozó kombinatorikai min-max tételek, így az egyik úthoz nagyon sok magyar matematikus neve kapcsolódik. Ezen eredmények bemutatásához be kell vezetnünk egy új gráfparamétert, és vissza kell mennünk az időben egészen Kőnig Dénes minden alapozó kurzus anyagában szereplő tételéig.
Egy gráfot párosnak mondunk, ha a csúcshalmazát fel tudjuk bontani két diszjunkt részhalmazra úgy, hogy a részeken belül nincs a gráfnak éle (azaz az eddigi foglalmakkal: két diszjunkt, független részhalmazra tudjuk bontani). Könnyű látni, hogy 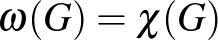 minden páros gráfra teljesül. Egy
minden páros gráfra teljesül. Egy  halmazt lefogó élhalmaznak mondunk, ha minden csúcsot „lefog”
halmazt lefogó élhalmaznak mondunk, ha minden csúcsot „lefog”  -ben, azaz nincs olyan csúcs a gráfban, amely ne lenne valamely
-ben, azaz nincs olyan csúcs a gráfban, amely ne lenne valamely  -beli él végpontja. A lefogó élek minimális számát
-beli él végpontja. A lefogó élek minimális számát  -ben
-ben  jelöli. Egy csúcsot izoláltnak mondunk, ha nincs olyan él a gráfban, amelynek végpontja lenne.
jelöli. Egy csúcsot izoláltnak mondunk, ha nincs olyan él a gráfban, amelynek végpontja lenne.
Tétel (Kőnig Dénes, 1931, [14]). Egy izolált csúcs nélküli  páros gráfra teljesül, hogy
páros gráfra teljesül, hogy 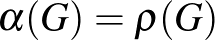 .
.
Ennek az eredménynek röviden vázolom egy következményét, mégpedig azt, hogy (izolált pont nélküli)  páros gráfban
páros gráfban 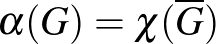 . (Mivel
. (Mivel 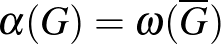 , ezért ez úgy is írható, hogy
, ezért ez úgy is írható, hogy  .)
.)
Vizsgáljuk meg Kőnig tételét, és vegyünk egy 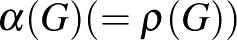 nagyságú
nagyságú  lefogó élhalmazt az izolált pont nélküli
lefogó élhalmazt az izolált pont nélküli  páros gráfban. Ezen
páros gráfban. Ezen 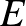 -beli élek olyanok, hogy egyrészt legfeljebb egy csúcsot tartalmazhatnak egy
-beli élek olyanok, hogy egyrészt legfeljebb egy csúcsot tartalmazhatnak egy  nagyságú független
nagyságú független  halmazból, másrészt minden csúcsot tartalmaznak
halmazból, másrészt minden csúcsot tartalmaznak  -ből, mint végpont. Sőt, az ún. Hall-tétel8 segítségével azt is elérhetjük, hogy az
-ből, mint végpont. Sőt, az ún. Hall-tétel8 segítségével azt is elérhetjük, hogy az  -en kívüli pontokat bepárosíthatjuk
-en kívüli pontokat bepárosíthatjuk  -be, azaz minden
-be, azaz minden  -en kívüli ponthoz hozzárendelhetünk egy saját, külön
-en kívüli ponthoz hozzárendelhetünk egy saját, külön  -beli szomszédot. Ha észrevételeinket
-beli szomszédot. Ha észrevételeinket  komplementerére lefordítjuk, akkor ott
komplementerére lefordítjuk, akkor ott  egy teljes részgráfot fog feszíteni és minden
egy teljes részgráfot fog feszíteni és minden  -en kívüli
-en kívüli  -beli csúcshoz lesz hozzárendelve egy olyan pont
-beli csúcshoz lesz hozzárendelve egy olyan pont  -ben, mellyel nem lesz összekötve (és minden
-ben, mellyel nem lesz összekötve (és minden  -en kívülihez más és más
-en kívülihez más és más  -beli lesz így hozzárendelve). Na de akkor
-beli lesz így hozzárendelve). Na de akkor  komplementerének kromatikus száma
komplementerének kromatikus száma 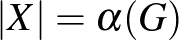 . Hiszen egyrészt legalább ennyi szín kell a színezéséhez, másrészt minden
. Hiszen egyrészt legalább ennyi szín kell a színezéséhez, másrészt minden  -en kívüli pontot színezzünk annak a (saját) pontjának a színével, akihez „nincs hozzákötve”
-en kívüli pontot színezzünk annak a (saját) pontjának a színével, akihez „nincs hozzákötve” 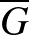 -ben. Tehát megkaptuk, amit szerettünk volna: izolált pont nélküli
-ben. Tehát megkaptuk, amit szerettünk volna: izolált pont nélküli  páros gráfban
páros gráfban 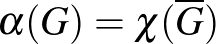 . Annak végiggondolását, hogy az izolált pont nem okoz gondot, és minden
. Annak végiggondolását, hogy az izolált pont nem okoz gondot, és minden  páros gráfban
páros gráfban 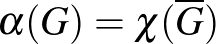 , az olvasóra bízzuk.
, az olvasóra bízzuk.
Kőnig Dénes egy másik, ún. élszínezési tételéből következik, hogy egy  páros gráf
páros gráf  élgráfjára teljesülnek az
élgráfjára teljesülnek az  és
és 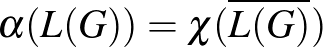 egyenlőségek. (Egy
egyenlőségek. (Egy  élgráfja az az
élgráfja az az  gráf, aminek a csúcsai
gráf, aminek a csúcsai  éleinek felelnek meg, és két csúcsa pontosan akkor van éllel összekötve, ha az eredeti
éleinek felelnek meg, és két csúcsa pontosan akkor van éllel összekötve, ha az eredeti  gráfban a két élnek volt közös végpontja.) Ezen kezdetek után egyre több gráfosztályra láttak be olyan típusú tételeket, hogy az osztályhoz tartozó
gráfban a két élnek volt közös végpontja.) Ezen kezdetek után egyre több gráfosztályra láttak be olyan típusú tételeket, hogy az osztályhoz tartozó  gráfokra
gráfokra 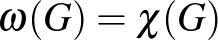 és
és 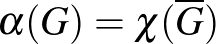 teljesül. Meg is említunk néhány példát.
teljesül. Meg is említunk néhány példát.
 Olyan gráfokat hívunk intervallumgráfnak, amelyek csúcsai megfeleltethetőek a valós számok egy-egy intervallumának, és két csúcs között pontosan akkor van él, ha a megfelelő intervallumok metszete nem üres. A fogalmat Hajós György vezette be [13]-ben, ahol egyből belátta, hogy
Olyan gráfokat hívunk intervallumgráfnak, amelyek csúcsai megfeleltethetőek a valós számok egy-egy intervallumának, és két csúcs között pontosan akkor van él, ha a megfelelő intervallumok metszete nem üres. A fogalmat Hajós György vezette be [13]-ben, ahol egyből belátta, hogy 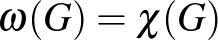 fennáll intervallumgráfokra. Később Gallai Tibor látta be, hogy
fennáll intervallumgráfokra. Később Gallai Tibor látta be, hogy 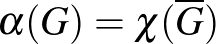 is igaz.
is igaz.

4. ábra. Egy intervallumgráf
 Azt mondjuk, hogy egy gráfban minden kör háromszögelt, ha nincsen benne feszített, legalább 4 hosszú kör9. Ilyen típusú gráfokra Berge látta be [1], hogy
Azt mondjuk, hogy egy gráfban minden kör háromszögelt, ha nincsen benne feszített, legalább 4 hosszú kör9. Ilyen típusú gráfokra Berge látta be [1], hogy 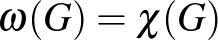 , valamint Hajnal András és Surányi János látták be [12], hogy
, valamint Hajnal András és Surányi János látták be [12], hogy 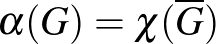 . Később Gallai Tibor [10] ez utóbbi eredményt erősítette és belátta, hogy elegendő feltenni, hogy minden legalább 5 hosszú páratlan körben van 2 „egymást nem metsző” átló10 ahhoz, hogy tudjuk
. Később Gallai Tibor [10] ez utóbbi eredményt erősítette és belátta, hogy elegendő feltenni, hogy minden legalább 5 hosszú páratlan körben van 2 „egymást nem metsző” átló10 ahhoz, hogy tudjuk 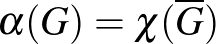 . Ennek az eredménynek később egy rövidebb bizonyítását adta Surányi László [23].
. Ennek az eredménynek később egy rövidebb bizonyítását adta Surányi László [23].
Azt láttuk, hogy magyar matematikusok aktív részvételével létrejöttek olyan tételek, amelyek azt mondják ki, hogy mind 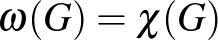 mind
mind 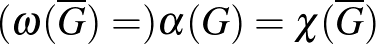 igaz bizonyos gráfosztályokban. Annak az észrevételnek az ellenőrzését az olvasóra bízzuk, hogy a fent említett gráfosztályok mind olyanok, amelyek zártak a feszített részgráfok képzésére, és máris megkapjuk a perfekt gráf sejtés egyik motivációját.
igaz bizonyos gráfosztályokban. Annak az észrevételnek az ellenőrzését az olvasóra bízzuk, hogy a fent említett gráfosztályok mind olyanok, amelyek zártak a feszített részgráfok képzésére, és máris megkapjuk a perfekt gráf sejtés egyik motivációját.
2.2. A másik út: Shannon kapacitás
Berge számára a másik fontos motivációt Claude Shannon 1956-ban megjelent cikke [20] jelentette, amiben bevezeti a Shannon kapacitás fogalmát11.
Az alapfeladatban adott egy ábécé (ennek elemeit egy  gráf
gráf  csúcshalmazával reprezentáljuk), amelyben bizonyos betűk összetéveszthetők egymással (az összetéveszthető betűpárok alkotják a gráf
csúcshalmazával reprezentáljuk), amelyben bizonyos betűk összetéveszthetők egymással (az összetéveszthető betűpárok alkotják a gráf  élhalmazát). Az ábécé betűiból készített két azonos hosszúságú szót összetéveszthetőnek nevezünk, ha minden pozícióban azonos vagy összetéveszthető betűk állnak. A kérdés, hogy legfeljebb hány
élhalmazát). Az ábécé betűiból készített két azonos hosszúságú szót összetéveszthetőnek nevezünk, ha minden pozícióban azonos vagy összetéveszthető betűk állnak. A kérdés, hogy legfeljebb hány  hosszú szót tudunk úgy készíteni, hogy semelyik kettő ne legyen egymással összetéveszthető? Ez a szám
hosszú szót tudunk úgy készíteni, hogy semelyik kettő ne legyen egymással összetéveszthető? Ez a szám  -ben exponenciálisan nő, és azt a mennyiséget, ahová ezeknek a számoknak a
-ben exponenciálisan nő, és azt a mennyiséget, ahová ezeknek a számoknak a  -edik gyöke tart12 a
-edik gyöke tart12 a  gráf Shannon kapacitásának nevezzük és
gráf Shannon kapacitásának nevezzük és  -vel jelöljük. Rövid vizsgálódás után
-vel jelöljük. Rövid vizsgálódás után  -re a következő egyenlőtlenségek adódnak:
-re a következő egyenlőtlenségek adódnak:
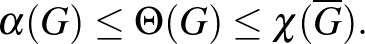
Shannon [20]-ban meghatározta minden legfeljebb 4-csúcsú gráf Shannon kapacitását és az 5-csúcsúakét is egy kivétellel, majd két kérdést tett fel:
1. kérdés Mik azok a minimális gráfok, amelyekre 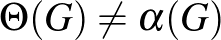 ?
?
2. kérdés Mennyi 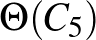 ?
?
Az első kérdés jól mutatja az 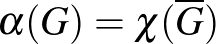 egyenlőség jelentőségét, ugyanis ha az fennáll, akkor a
egyenlőség jelentőségét, ugyanis ha az fennáll, akkor a 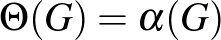 is teljesül. Nagyon röviden ez volt a második motiváció, aminek mentén Berge eljutott a perfekt gráfok fogalmához. Míg a második kérdést azért is fontos kiemelni, mert azt is Lovász László válaszolta meg [17]-ben.
is teljesül. Nagyon röviden ez volt a második motiváció, aminek mentén Berge eljutott a perfekt gráfok fogalmához. Míg a második kérdést azért is fontos kiemelni, mert azt is Lovász László válaszolta meg [17]-ben.
A fent leírt két útnak köszönhetően talán az olvasó is kaphatott egy képet arról, hogy hogyan épülnek egymásra az eredmények, és hogy léteznek közös motivációk a háttérben.
2.3. Berge gráfosztályai
A motivációkat és előzményeket bemutató részt Berge gráfosztályaival zárjuk:
1. osztály: olyan  gráfok, amelyekre
gráfok, amelyekre 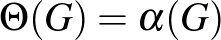 .
.
2. osztály: olyan  gráfok, amelyekre
gráfok, amelyekre 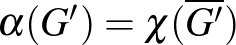 teljesül minden
teljesül minden  feszített részgráfjára
feszített részgráfjára  -nek. 13
-nek. 13
3. osztály: olyan  gráfok, amelyekre
gráfok, amelyekre 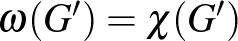 teljesül minden
teljesül minden  feszített részgráfjára
feszített részgráfjára  -nek.
-nek.
4. osztály: olyan  gráfok, amelyek nem tartalmaznak sem legalább 5 hosszú páratlan kört, sem azok komplementerét, mint feszített részgráfot.
gráfok, amelyek nem tartalmaznak sem legalább 5 hosszú páratlan kört, sem azok komplementerét, mint feszített részgráfot.
Egy 1960-ban tartott szemináriumon Berge azt a kérdést tette fel, hogy igaz-e, hogy a 4. osztályban lévő gráfok az 1. osztályban is benne vannak? Míg 1963-as dolgozatában [2] a következőket kérdezte:
3. kérdés Igaz-e, hogy a 2. osztály és a 3. osztály ugyanazokat a gráfokat tartalmazza?
4. kérdés Igaz-e hogy a 3. osztály és a 4. osztályban ugyanazok a gráfok vannak?
Ezek a kérdések már ismerősök lehetnek:
 Ha a 2. osztály és a 3. osztály elemei megegyeznek, az az
Ha a 2. osztály és a 3. osztály elemei megegyeznek, az az 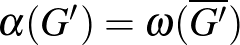 összefüggés miatt épp azt jelenti, hogy egy gráf pontosan akkor perfekt, ha a komplementere perfekt. Tehát itt a perfekt gráf sejtést látjuk.
összefüggés miatt épp azt jelenti, hogy egy gráf pontosan akkor perfekt, ha a komplementere perfekt. Tehát itt a perfekt gráf sejtést látjuk.
 Ha a 3. osztály egybeesik a 4. osztállyal, az pedig azt jelenti, hogy pontosan azok a gráfok perfektek, amelyek sem legalább 5 hosszú páratlan kört, sem azok komplementerét nem tartalmazzák, mint feszített részgráfot. Ez pedig maga az erős perfekt gráf sejtés.
Ha a 3. osztály egybeesik a 4. osztállyal, az pedig azt jelenti, hogy pontosan azok a gráfok perfektek, amelyek sem legalább 5 hosszú páratlan kört, sem azok komplementerét nem tartalmazzák, mint feszített részgráfot. Ez pedig maga az erős perfekt gráf sejtés.
Ez volt a perfekt gráfok, a perfekt gráf sejtés, valamint az erős perfekt gráf sejtés keletkezésének zanzásított története. Amit meg szerettem volna mutatni, és valamennyire fel akartam idézni, az az, hogy hány különböző terület képviselőit érdekelt a sejtés, és hogy mennyire centrális szerepe volt a megoldásnak a '70-es évek elején. Akinek esetleg sikerült felkelteni az érdeklődését a perfekt gráfok (és történetük) iránt (és nem ismeri a vonatkozó irodalmat), annak melegen ajánljuk Berge [3] cikkét, illetve annak kiegészített újraközlését [4], amelyben kimerítő, szinte hónapról hónapra leírt történettel szolgál arról, hogy hogyan merült fel a fogalom, hogyan születtek, majd konferenciáról konferenciára közvetítődtek a perfekt gráfokkal kapcsolatos eredmények az '50-es évek végén és a '60-as években.
3. Néhány szó a bizonyításról és az utóbbi évtizedek eredményeiről
Természetesen a bizonyítás teljes ismertetése túlfeszítené a cikk kereteit, így csak egy lényeges dolgot említünk meg nagyon röviden. Lovász László (először megjelent, azaz [15]-beli) bizonyításának fő összetevője az ún. többszörözési lemma volt. A többszörözési lemma azt mondja, hogy ha egy perfekt gráf egy  pontját egy teljes gráffal helyettesítjük abban az értelemben, hogy a teljes gráf minden pontja a
pontját egy teljes gráffal helyettesítjük abban az értelemben, hogy a teljes gráf minden pontja a  eredeti szomszédaival van öszekötve, akkor perfekt gráfot kapunk. Ennek a lemmának a segítségével lehetett eljutni a Fulkerson [9] által megkezdett úton a sejtés bizonyításáig. (Megjegyezzük, hogy a perfekt gráf tételre manapság a legtöbb helyen egy Gaspariantól [11] származó bizonyítás „van forgalomban”.)
eredeti szomszédaival van öszekötve, akkor perfekt gráfot kapunk. Ennek a lemmának a segítségével lehetett eljutni a Fulkerson [9] által megkezdett úton a sejtés bizonyításáig. (Megjegyezzük, hogy a perfekt gráf tételre manapság a legtöbb helyen egy Gaspariantól [11] származó bizonyítás „van forgalomban”.)
Akit jobban érdekel a téma és a legújabb fejlemények, annak ajánlom Schrijver monográfiájának [21] megfelelő fejezeteit, valamint a Ramírez Alfonsín és Reed által szerkesztett kötetet [19]. Két áttörést feltétlenül ki kell még emelnünk. Egyrészt azóta kiderült, hogy polinom időben el lehet dönteni, hogy egy gráf perfekt-e [5,8]. Másrészt – utolsó mondatként – kerüljön ide, hogy a Chudnovsky–Robertson–Seymour–Thomas szerzőnégyesnek 2003-ban sikerült belátni az erős perfekt gráf sejtést [6,7].
Irodalomjegyzék
- [1] C. Berge. Farbung von Graphen, deren samtliche bzw. deren ungerade Kreise starr sind. Wissenschaftliche Zeitschrift Martin Luther Univ. Halle-Wittenberg, 10 (1961), 114–115.
[2] C. Berge. Some classes of perfect graphs. Six Papers on Graph Theory. (related to a series of lectures at the Research and Training School of the Indian Statistical Institute, Calcutta, 1963) 1–21.
[3] C. Berge. Motivations and history of some of my conjectures. Discrete Mathematics, 165 (1997), 61–70.
[4] C. Berge, J. R. Ramírez Alfonsin. Origins and genesis. In: Perfect graphs, Wiley, 44, (2001), 1–12.
[5] M. Chudnovsky, G. Cornuéjols, X. Liu, P. Seymour, K. Vušković, Recognizing berge graphs. Combinatorica, 25(2) (2005), 143–186.
[6] M. Chudnovsky, N. Robertson, P. D. Seymour, R. Thomas. The strong perfect graph theorem. Annals of Mathematics, (2006), 51–229.
[7] M. Chudnovsky, N. Robertson, P.D. Seymour, R. Thomas. Progress on perfect graphs. Mathematical Programming, 97(1) (2003), 405–422.
[8] G. Cornuéjols, X. Liu, K. Vuskovic. A polynomial algorithm for recognizing perfect graphs. In 44th Annual IEEE Symposium on Foundations of Computer Science, 2003. Proceedings. (pp. 20–27). IEEE.
[9] D. R. Fulkerson. Anti-blocking polyhedra. Journal of Combinatorial Theory, Series B, 12(1) (1972), 50–71.
[10] T. Gallai. Graphen mit triangulierbaren ungeraden Vielecken. Magyar Tud. Akad. Mat. Kutato Int. Közl. 7 (1962), 3–36.
[11] G. S. Gasparian. Minimal imperfect graphs: a simple approach. Combinatorica, 16(2) (1996), 209–212.
[12] A. Hajnal, J. Surányi. Über die Auflösung von Graphen in vollständige Teilgraphen. Ann. Univ. Sci. Budapest, Eötvös Sect. Math., 1 (1958), 113–121.
[13] Gy. Hajós. (problem 65) Über eine art von graphen. Internationale Mathematische Nachrichten, 11, 1957.
[14] D. Kőnig. Gráfok és mátrixok. Matematikai és Fizikai Lapok, 38 (1931), 116–119.
[15] L. Lovász. Normal hypergraphs and the perfect graph conjecture. Discrete Mathematics, 2(3) (1972), 253–267.
[16] L. Lovász. A characterization of perfect graphs. Journal of Combinatorial Theory, Series B, 13(2) (1972), 95–98.
[17] L. Lovász. On the Shannon capacity of a graph. IEEE Transactions on Information theory, 25(1) (1979), 1–7.
[18] J. Mycielski. Sur le coloriage des graphes, Colloq. Math., 3 (1955), 161–162.
[19] J. L. Ramírez-Alfonsín, B. A. Reed. Perfect graphs (Vol. 44). Wiley, 2001.
[20] C. Shannon. The zero error capacity of a noisy channel. IRE Transactions on Information Theory, 2(3) (1956), 8–19.
[21] A. Schrijver. Combinatorial optimization: polyhedra and efficiency (Vol. 24). Springer Science & Business Media, 2003.
[22] T. B. Schwarcz. Gráfok Shannon kapacitása, MSc dolgozat, ELTE, 2018.
[23] L. Surányi. The covering of graphs by cliques, Stud. Sci. Math. Hungar 3 (1968), 345–349.
Lábjegyzetek
- 1 Egy másik lehetséges definíciója a feszített részgráfnak, hogy
 -ből csúcsokat (és hozzájuk tartozó éleket) hagyunk el.
-ből csúcsokat (és hozzájuk tartozó éleket) hagyunk el. - 2 Izomorfián olyan bijekciót értünk 2 gráf csúcshalmaza között, amely élt élbe és nem élt nem élbe visz.
- 3 Szokták stabil csúcshalmaznak is hívni.
- 4 Ugyan nem tartozik szorosan a cikk témájához, de felmerülhet az olvasóban a kérdés, hogy vajon
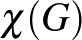 -t tudjuk-e
-t tudjuk-e 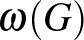 valamilyen függvényével felülről is becsülni. A meglepő valász az, hogy nem: Mycielski [18] bizonyította, hogy minden
valamilyen függvényével felülről is becsülni. A meglepő valász az, hogy nem: Mycielski [18] bizonyította, hogy minden 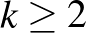 egész számhoz létezik olyan
egész számhoz létezik olyan 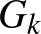 gráf, melyre
gráf, melyre 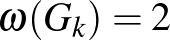 és
és 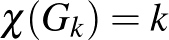 .
. - 5 francia matematikus, 1926–2002
- 6 A feszített kört angolul hole-nak, magyarul üregnek is mondják néhol a szakirodalomban, mi a „kört feszített részgráfként” terminust fogjuk használni.
Érdekesség, hogy Berge semi Gallai gráfoknak hívta a páratlan kört feszített részgráfként nem tartalmazó gráfokat, ami ellen Gallai tiltakozott, így Berge megváltoztatta a fogalom nevét. - 7 Tételekhez a cikk megjelenésének évét szokták odaírni, de a bizonyítás 1971-ben született.
- 8 A Hall-tétel vagy angolul Hall's marriage theorem arra ad szükséges és elégséges feltételt, hogy egy páros gráfban a csúcshalmaz egyik osztálya mikor „párosítható be” a másik osztályba.
- 9 Annak kitalálását, hogy honnan jöhet a háromszögeltség elnevezés, és mi lehet egy, a nevet jobban tükröző ekvivalens definíció, az olvasóra bízzuk.
- 10 Ami ekvivalens azzal, hogy bármely legalább 5 hosszú páratlan kör háromszögelt.
- 11 June 1957: When he heard that I was writing a book on graph theory, my friend M.P. Schutzenberger drew my attention on an interesting paper of Shannon which was presented at a meeting for engineers and statisticians, but which could have been missed by mathematicians working in algebra or combinatorics. (idézet [3,4] )
- 12 Hogy valóban létezik ez a határérték, illetve részletesebb leírásokért lásd például [22]
- 13 Itt
 a
a 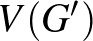 csúcshalmazra vonatkoztatott komplementere
csúcshalmazra vonatkoztatott komplementere 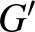 -nek.
-nek.
Vizer Máté
Rényi Alfréd Matematikai Kutatóintézet









