Ebben a cikkben röviden összefoglalom azokat a lehetőségeket, amelyeket a Regula Falsi módszerének alkalmazása jelent az általános iskolai oktatásban. Ez a hatékony feladatmegoldási eszköz a matematikai oktatási gyakorlatban alig van jelen, és akkor is csak a szisztematikus próbálgatás fedőnév alatt. Mutatok néhány megoldási ötletet a 8. osztályos matematika felvételi feladatsorokban található szöveges feladatok megoldására. Mivel a felvételin a szöveges feladatok megoldása sok tanuló számára nehézséget jelent, ezért vetettem fel azt az ötletet, hogy a Regula Falsi módszerét érdemes implementálni a magyar oktatási gyakorlatba.
1. Nehézségek az aritmetikai módszerekről az algebrai eszközökre történő áttérés során
Gyakorló matematikatanárként tapasztalom, hogy a 8. osztályos felvételin a tanulók jelentős része a szöveges feladatok megoldása során nem boldogul az algebra eszközeivel, ezért vagy kihagyja a feladatot, vagy a megoldás során próbálgatásokba bocsátkozik. Ez a tény összhangban van számos nemzetközi kutatás eredményeivel, amelyek alátámasztják, hogy a 14–15 éves tanulók a számukra újszerű szöveges feladatok megoldásakor a helyes választ próbálgatással adják meg, ezeket a nemzetközi szakirodalomban „guess-and-check” vagy „trial-and-error” néven említik [11]. Ennek egyik fő oka az, hogy a 8. évfolyamos tanulók többségének az ismeretei a pre-algebra [1] fázisában vannak, vagyis rendelkeznek az alapvető aritmetikai ismeretekkel, ismerik a műveletek tulajdonságait, a változó, illetve ismeretlen fogalmát, és meg tudnak oldani egyenleteket lebontogatással, illetve mérlegelvvel. Viszont a tanulók többsége még nem rendelkezik megalapozott algebrai tudással, ezért nehézségeik vannak a szöveges feladatokban szereplő adatok közötti összefüggések betűszimbólumokkal történő felírásával. Az egyenlőségjelre nem úgy tekintenek, mint egy ekvivalenciát kifejező szimbólumra (amelynek jobb, illetve bal oldalán egyenértékű kifejezések állnak), hanem mint egy olyan írásjelre, amelynek jobb oldalán a bal oldalon szereplő műveletek eredménye kell álljon [9]. Továbbá nincs megfelelően kifejlődve az a strukturális gondolkodás, amely ahhoz szükséges, hogy az adott matematikai probléma teljes szerkezetét átlássák [2], [8]. Ezáltal gondot okoz nekik a szöveges feladatok lefordítása az algebra nyelvére, vagyis helytelenül írják fel az egyenletet egy szöveges feladat megoldása során. Hasonló következtetésekre jutottunk, amikor az általános iskolai tanulók problémamegoldó képességeit vizsgáltuk a szöveges feladatok esetében [6].
2. A hamis feltételezések módszere, avagy a Regula Falsi
A fentiekben felsorolt tényeket figyelembe véve jogosan vetődik fel az a kérdés, hogy a szöveges feladatok megoldásának eszközéül kizárólag az algebrai ismereteket válasszuk, vagy alkalmazzunk egyéb módszereket is az oktatási folyamat során? Mivel a tanulók zömében próbálgatással dolgoznak, ezért indokolt lehet ezeket a próbálgatásokat szisztematikussá tenni, ez a feladatok megoldása során a számolások mennyiségét jelentősen csökkenti. Egy ilyen módszer lehet a hamis feltételezések módszere, amelyet a szakirodalom regula falsi néven említ. A módszer az aritmetikának egy sajátos feladatmegoldási módszere, amelyet két- vagy három ismeretlenes feladatok esetében is alkalmazhatunk. A módszer lényege: a feladat ismeretlen mennyiségeire nézve valamilyen feltételt (feltételeket) állítunk és összehasonlítjuk a valódi helyzetet (a feladat adatait) a hipotézisek által létrehozott helyzettel. Az eltérés figyelembevételével egyszerű számolások segítségével könnyen következtethetünk arra, hogy mennyiben tér el a hamis feltételezés a helyes megoldástól. Érdemes hangsúlyozni, hogy a hamis feltételezések módszere különbözik az egyszerű próbálgatásoktól és nem a „megoldás eltalálása” a fő célkitűzés. A legfőbb különbséget az jelenti, hogy a hipotézisek felállítása után megpróbálunk következtetni arra, hogy milyen irányban és mennyivel változtassuk meg a feladat ismeretlen mennyiségeit ahhoz, hogy a jó megoldást megtaláljuk. A módszer előnye rövid távon az, hogy jelentősen csökkenti a számolások mennyiségét az egyszerű próbálgatásokhoz viszonyítva. Mivel a tanuló az általa választott adatokkal számol és közben az adatok közötti összefüggéseket vizsgálja, ezzel egyre jobban átlátja a szöveges feladatok teljes szerkezetét. Ez pedig jelentős hatással van a strukturális gondolkodás fejlődésére, amely a szöveges feladatok algebrai úton való megközelítésének egyik alapvető feltétele. A hamis feltételezések módszerének tanórai bevezetésével kapcsolatban elért eddigi eredményeinkről két tanulmányban is beszámoltam [4], [5]. Jelen tanulmányban egy rövid tudománytörténeti áttekintés után a módszer alkalmazását mutatnám be néhány 8. osztályos felvételi feladat esetében.
A módszerre vonatkozó legrégebbi írásos emlékek Kr.e. 2000 év körüliek. A módszer történelmi vonatkozásait egy másik tanulmányban már bemutattam [3], ezért itt csak a 18. századi európai aritmetika oktatásban fellelhető két mozzanatra térnék ki. Maróthi György Arithmetika című könyvében [10] bemutatja a Mesés Regula szabályát, amelyről a következőket írja:„178. §. Amit deákul Regula Falsi-nak hívnak, azért neveztem magyarul Mesés Regulának, mert ezen szokták leginkább megfejteni a Meseforma kérdéseket, amelyekkel a Számvetők egymást próbálgatják. Deákul azért hívják Regula Falsinak, mert mikor rajta meg akarják fejteni a Mesét, elsőben csak ráfogják vaktában valamely számra, hogy ez az, amelyet keresnek, jóllehet nem az. De osztán ebből a hamis számból találják ki a kérdésben levő igazi számot, amint mindjárt megmondjuk.”
Ezek után következik az egyes regula falsi módszerének bemutatása a következő feladat megoldásával.
Egy leánytól kérdik a Leányt kérők, hány esztendős? Az anyám úgymond harmadfél annyi idős, mint én: az Atyám pedig háromszor annyi idős. A hármunk ideje tészen 117 esztendőt. Kérdés, hány esztendős volt?
A módszer lényege, hogy a lány életkorára egy tetszőleges számot választva kiszámítható a hármuk életkorának összege. Utána megvizsgáljuk ennek az összegnek és a 117-nek az arányát. A leány valós életkorát az általunk választott életkor és a kapott arány ismeretében számítjuk ki.
Az egyes regula falsi alkalmazására tekintsük az Országos Matematika Felvételi, 2014. január 18., 8. feladatát (a továbbiakban a felvételi feladatokra OMF 2014. január 18./8. módon fogunk hivatkozni).
A nekeresdi piacon 12 kg első osztályú és 8 kg másodosztályú almát vásároltunk. A másodosztályú alma kilogrammonkénti ára az első osztályú alma kilogrammonkénti árának 75%-a volt. Összesen 4176 tallért fizettünk. Hány tallér az első osztályú és a másodosztályú alma kilogrammonkénti ára? Írd le a számolás menetét is!
Elsőként feltételezzük például, hogy az első osztályú alma kilogrammonkénti ára 100 tallér, míg a másodosztályú almáé 75 tallér. Ebben az esetben a 12 kg első osztályú és a 8 kg másodosztályú alma ára összesen 1800 tallér. A feladatban viszont összesen 4176 tallérba, vagyis az általunk feltételezett ár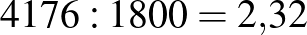 
-szorosába került a vásárlás. Tehát az almák valódi ára az általunk feltételezett ár 2,32-szorosa, így az első osztályú almából egy kg 232 tallérba, míg a másodosztályú almából 174 tallérba kerül.
A fenti gondolatmenettel könnyen megoldhatók az OMF 2018. január 25./10., OMF 2019. január 19./6. Az utóbbi feladathoz mellékelt javítási útmutatóban az egyik módszernél felfedezhetők az egyes regula falsi szabályának bizonyos jelei.
Edward Hatton könyvében találunk egy részletes leírást a kettős regula falsi számolási szabályaira vonatkozóan [7]. Ebben az esetben a megoldás során két feltételezést használunk és a számolási szabály egy szigorú algoritmus mechanikus alkalmazásán alapul. A módszer viszonylag körülményes, ennek ellenére a 18. század aritmetikájában népszerű volt. Nagy hátránya viszont, hogy csak a feladat konkrét megoldására szolgált. Ezért eredeti formájában nem illeszthető be a mai oktatási stratégiák közé, mivel napjainkban a feladatok megoldásán túl a strukturális gondolkodás fejlesztése is egy alapvető célkitűzés. Ezért vizsgáltuk meg azokat a lehetőségeket, hogy a kettős feltételezésen alapuló feladatmegoldási módszereket milyen módon kell úgy átalakítani, hogy azokat bevezethessük a mai oktatási gyakorlatba. A továbbiakban néhány konkrét feladaton keresztül szemléltetnénk a módszer lényeges jegyeit.
3. Hogyan oldjunk meg szöveges feladatokat a Mesés Regulával?
Tekintsünk kezdetben egy olyan felvételi feladatot (OMF, 2006. január 28./8.), amelyhez hasonlókat már alsóbb osztályokban is tanítunk nemcsak aritmetikai módszerekkel, hanem különböző képi reprezentációkkal is (gondoljunk például a mindannyiunk által jól ismert feladatra, ahol egy udvarban tyúkok és nyulak vannak, az ismert adatok pedig a fejek, illetve a lábak száma, ebből kell kiszámítani az egyes állatok számát).
A szerelők 155 méter hosszú útvonalon vízvezeték csövet fektettek le nyolc méteres és öt méteres darabokból. Összesen 25 darab csövet használtak fel. Hány db 8 m-es és hány db 5 m-es cső kellett? Írd le a megoldás gondolatmenetét!
A feladat algebrai modellje a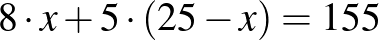 
egyenlet, viszont ennek a felírása a tanulók többségének gondot okoz. Ennek egyik oka, hogy nem tudják helyesen felírni az adatok közötti összefüggéseket (ha a 8 m-es csövek száma 
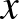, akkor az 5 m-eseké 
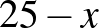), valamint az egyenlet felírásakor mellőzik a 8-as, illetve 5-ös szorzókat. Ezért a leggyakrabban előforduló hibásan felírt egyenletek a következők: 
, 
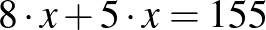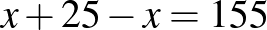, illetve az 
.
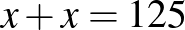A többféle aritmetikai módszer közül a következőt emelnénk ki. Kezdetben feltételezzük, hogy minden cső 5 m-es. Ennek alapján a csövek együttes hossza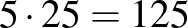 
m, amely 30 m-rel rövidebb a feladatban szereplő adatnál. Viszont, ha egy 5 m-es csövet 8 m-esre cserélünk, akkor a csövek együttes hossza 3 m-rel növekszik (miközben a csövek száma változatlan marad), így összesen 
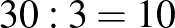ilyen „cserére” van szükség. Tehát 10 darab 8 m-es és 15 darab 5 m-es csőre van szükség.
Hasonló gondolatmenettel oldhatók meg az OMF 2007. február 1./5. és OMF 2013. január 19./8. feladatok is.
A fentiekben bemutatott módszer a kettős regula falsi módszerének egy alapvető változata, mivel az első feltételezés 25 db 5 m-es és 0 db 8 m-es cső) és a második feltételezés (24 db 5 m-es és 1 db 8 m-es cső) során vizsgáljuk a feltételezés hibájának alakulását. Tehát a fenti gondolatmenet magában hordozza a kettős reguls falsi alkalmazásának szabályát, amelyet a következő feladatokban részletesebben bemutatunk. Kezdetben tekintsünk egy viszonylag egyszerű feladatot, amelyet a tanulók többsége algebrai módszerekkel is képes megközelíteni (OMF 2010. január 23./8.).
Egy kollégium négy épületében összesen 436 diákot helyeztek el. Az első épületben 10 diákkal több van, mint a negyedikben, a negyedikben pedig 8 diákkal több van, mint a harmadikban. A második épületben viszont 10 diákkal van több, mint a harmadikban. Hány diák lakik az egyes épületekben? Írd le a megoldás menetét is!
1. feltételezés: Kezdetben feltételezzük, hogy az első épületben 50 diák van, majd a feladat adatai közötti összefüggéseket figyelembe véve adódik, hogy a másodikban 42, a harmadikban 32, míg a negyedikben 40 diák van, így a diákok száma összesen 164. A feladatban viszont összesen 436 diák szerepel, tehát a feltételezésünk hibája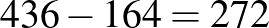 
.
2. feltételezés: Az előző feltételezéshez képest az első épületben lévő diákok számát eggyel növeljük. Így az első épületben 51, a másodikban 43, a harmadikban 33, a negyedikben pedig 41 diák van, ez összesen 168 diákot jelent. Így a feltételezés hibája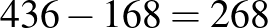 
.
Belátható, hogy az első épületben lévő diákok számát eggyel növelve a feltételezés hibája 4-gyel csökken. Így, az első feltételezésből kiindulva, ha az első épületben elszállásolt diákok számát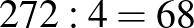 
-cal növeljük, akkor a feltételezés hibája 0-ra csökken. Tehát az első épületben 118, a másodikban 110, a harmadikban 100, a negyedikben pedig 108 diák lakik. Megfigyelhető, hogy a feladat megoldása során a tanulók az általuk választott számadatokkal dolgozhatnak, viszont a két feltételezés során következtetéseket kell megfogalmazniuk az adatok változása és a feltételezés hibájának az alakulása között, majd ezek alapján konkrét aritmetikai számításokkal megtalálják a helyes eredményt.
Hasonlóan gondolkodva oldhatjuk meg az OMF 2009, január 29./10., OMF 2017. január 21./6., OMF 2018. január 25./6. és 7., OMF 2019. január 24./10., OMF 2021. január 23./6., OMF 2022.január 27./8. feladatokat.
A fenti feladat esetében jogosan vetődik fel a kérdés, hogy miért szükséges ezzel a módszerrel dolgozni, amikor a megoldáshoz szükséges algebrai egyenlet viszonylag egyszerűen felírható, vagy a tanuló dolgozhat a szakaszos ábrázolás módszerével is (bár a javítókulcsban kizárólag az algebrai módszer jelenik meg). Viszont a tapasztalat szerint jelentős számban akadnak tanulók, akiknek még egy ilyen viszonylag egyszerű feladat is bonyodalmat okoz. Így hasznosnak bizonyulhat, ha egy megoldási módszerrel több van a tanulói tudástárban.
Léteznek viszont olyan felvételi feladatok is, amelyek megoldása a legtöbb tanuló számára gondot okoz, ehhez tekintsük például a következő felvételi feladatot (OMF 2013. január 24./8.):
Egy dobozban számkártyák vannak, minden kártyán van egy szám. Az összes kártya 75%-án páros szám van, a többi számkártyán páratlan szám van. Ha kiveszünk a dobozból öt páros, és öt páratlan számot tartalmazó számkártyát, akkor a dobozban maradó számkártyák pontosan hatodán lesz páratlan szám. Összesen hány számkártya volt eredetileg a dobozban? Írd le a számolás menetét is!
A feladat megoldása során az első feltételezést könnyen megtehetjük a kártyák százalékos megoszlásából kiindulva.
1. feltételezés: 25 páratlan és 75 páros számkártya van a dobozban. Ha kiveszünk öt páros és öt páratlan számkártyát, akkor 20 páratlan és 70 páros számkártya marad. Mivel a dobozban maradó számkártyák között 5-ször annyi páros van, mint ahány páratlan, következik, hogy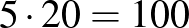 
darab páros számkártya kéne legyen. Tehát a feltételezés hibája 
.
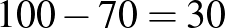2. feltételezés: Eggyel növeljük a páratlan számkártyák számát, így 26 páratlan és 78 páros számkártya van (háromszor annyi páros számkártya van, mint páratlan). A megfelelő számú kártyákat kivéve 21 páratlan és 73 páros marad. Az 1. feltételezésnél bemutatott gondolatmenet szerint a feltételezés hibája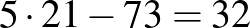 
lesz.
Tehát a páratlan számkártyák számát eggyel növelve a feltételezés hibája kettővel növekszik. Így az első feltételezéshez képest a páratlan számkártyák számát 15-tel kell csökkenteni ahhoz, hogy a feltételezés hibája 0-ra csökkenjen. Ebből következik, hogy eredetileg 10 páratlan és 30 páros számkártya volt a dobozban.
Ebben a feladatban a legfőbb nehézséget az adatok közötti összefüggések betűszimbólummal való megközelítése, majd az egyenlet felírása okozza, ezzel magyarázható, hogy a legtöbb tanuló képtelen megbirkózni a feladattal. A hamis feltételezések módszerével viszont a tanulók konkrét, általuk választott számadatokkal dolgozhatnak, következtethetnek, kikerülve ezáltal a betűszimbólumokkal való manipulálás nehézségeit.
Hasonló gondolatmenettel oldhatók meg az OMF 2011. január 27./10., OMF 2020. január 18./10., illetve OMF 2020. január 23./8. feladatok is.
Adódnak olyan helyzetek is, amikor a feladatban szereplő számadatok miatt indokolt egy „visszafelé gondolkodás”. Ehhez tekintsünk egy másik felvételi feladatot (OMF 2016. január 21./10.).
Az iskolai énekkarban kétszer annyi lány van, mint fiú. Betegség miatt az énekkari próbán 3 fiú és 3 lány nem tudott részt venni, a többiek viszont valamennyien ott voltak. Így az énekkari próbán részt vevő fiúk száma a lányok számának 
része volt. Hány lány és hány fiú tagja van az énekkarnak?
Ebben az esetben könnyebben célt érünk, ha a bonyolultabb összefüggéseket tartalmazó végső helyzetből kiindulva fogalmazzuk meg a feltételezéseket.
1. feltételezés: A próbán résztvevő lányok száma 90, míg a fiúk száma 40. Tehát az iskolai énekkarban 93 lány és 43 fiú van. Mivel a lányok száma kétszerese a fiúk számának, ezért a feltételezés hibája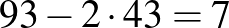 
.
2. feltételezés: A próbán résztvevő lányok száma 99, míg a fiúk száma 44. Így az iskolai énekkarban 102 lány és 47 fiú van, a feltételezés hibája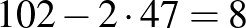 
. Ebből következik, hogy a lányok számát 9-cel emelve a feltételezés hibája eggyel növekszik.
Tehát ha azt akarjuk, hogy a hiba 7-tel csökkenjen, akkor a lányok számát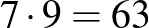 
-mal kell csökkenteni az első feltételezéshez képest. Így a lányok száma 27, míg a fiúk száma ennek a része, azaz 12. Ehhez hozzáadva a próbáról hiányzó 3 fiút és 3 lányt, adódik, hogy az énekkarban 30 lány és 15 fiú van. Ez viszont eleget tesz a feladatban szereplő feltételnek, amely szerint a lányok száma a fiúk számának a kétszeresével egyenlő.
A fenti gondolatmenet bonyolultnak tűnhet, viszont érdemes megjegyezni, hogy a felvételiző tanulók nagyon kis részaránya képes helyesen felírni a feladat megoldásához szükséges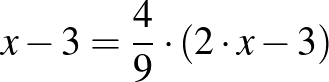 
egyenletet.
Hasonlóan gondolkodva járhatunk el az OMF 2014. január 23./10., OMF 2015. január 17./10., OMF 2017. január 21./10. feladatok esetében is..
A törtegyütthatós egyenletek felírása során tapasztalható nehézségek főként a betűszimbólumokkal történő manipulációval kapcsolatosak, vagyis a tanulók nehezebben dolgoznak olyan algebrai kifejezésekkel, ahol az együtthatók törtszámok. Tekintsük például a következő feladatot (OMF 2015. január 22./8.).
Egy szám felének és harmadának az összege 49-cel nagyobb, mint a szám negyede. Melyik ez a szám? Válaszodat számítással indokold!
A feladat megoldható tipikusan aritmetikai eszközökkel, viszont itt is gondot okozhat a törtrészek és a feladatban szereplő számadat (konkrétan a 49) megfeleltetése. A hamis feltételezések módszerével lehetőség adódik arra, hogy a tanuló általa gondolt konkrét számok törtrészeivel számoljon, ez jelentősen megkönnyíti a számolási eljárást. A feladat adatait figyelembe véve célszerű 12-vel osztható számokra gondolni. Így például kiindulhatunk a következő feltételezésekből.
1. feltételezés: Legyen a gondolt szám 12. Akkor a felének és harmadának összege 7-tel több a szám negyedénél, vagyis a feltételezés hibája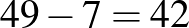 
.
2. feltételezés: Legyen a gondolt szám 24. Ebben az esetben a felének és harmadának összege 14-gyel több a szám negyedénél, a feltételezés hibája pedig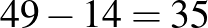 
.
Belátható, hogy a gondolt számot 12-vel növelve a feltételezés hibája 7-tel csökken, tehát az első feltételezéshez képest a gondolt számot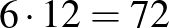 
-vel kell növelni, így a feladat megoldása 
.
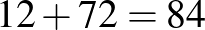Megjegyzésünk, hogy a fenti feladatot az egyes regula falsi szabályával is meg lehet oldani. Az első feltételezésnél a szám felének és harmadának összege 7-tel nagyobb a szám negyedénél. A feladatban viszont ez a különbség 49, így adódik, hogy a feltételezett számnak a hétszeresét véve megkapjuk a helyes eredményt, ami 84. Ez a módszer gyorsabb a kettős regula falsi alkalmazásánál, viszont bizonyos esetekben félrevezető is lehet.
A fenti feladatban alkalmazott kettős regula falsi módszere alkalmazható az OMF 2008. január 26./5., OMF 2009. január 24./8., illetve OMF 2015. január 17./8. feladatok esetében is.
Összefoglalva, a hamis feltételezések módszerének tanítása nem helyettesítheti, hanem hatékonyan kiegészítheti az iskolai tananyagban szereplő aritmetikai és algebrai módszereket. Olyan feladatok megoldására kínál egy alternatívát, amelyeknek a tanult aritmetikai vagy algebrai eszközökkel való megközelítése bonyolult. Egy évfolyamon belül lehetőséget nyújt a differenciálásra: azok a tanulók, akik számára az algebrai módszerek elsajátítása bonyolult, dolgozhatnak a hamis feltételezések módszerével, miközben társaik már az algebra eszközeit használják. Amint már említettük, a módszer jelentős szerepet játszik a strukturális gondolkodás fejlesztésében és így az algebrára való áttérésben. Mivel az algebrai ismeretek megszilárdulásával a hamis feltételezések módszere háttérbe szorul, ezért nem kell attól tartani, hogy a hamis feltételezések módszere teljesen kiszorítaná a szöveges feladatok algebrai úton való megközelítését.
Irodalomjegyzék
- [1] G. Boulton-Lewis, H. Pillay, L. Wills. Sequential development of algebra knowledge: a cognitive analysis. Mathematics Education Research Journal, Vol 10/2, 1998.
- [2] E. Filloy, T. Rojano. Solving equations, the transition from arithmetic to algebra. For the Learning of Mathematics, 9 (2), 1989.
- [3] Zs. Fülöp, Feladat megoldási módszerek összehasonlító vizsgálata a pedagógus, illetve a diák rendelkezésére álló ismeretek birtokában. Doktori értekezés, Matematika és Számítástudományok Doktori Iskola, Szeged, 2017.
- [4] Zs. Fülöp. Regula falsi in lower secondary school education. Teaching Mathematics and Computer Science, 14 / 2, 2016.
- [5] Zs. Fülöp. Regula falsi in lower secondary school education II. Teaching Mathematics and Computer Science, 18 / 2, 2020.
- [6] Zs. Fülöp. Transition from arithmetic to algebra in primary school education. Teaching Mathematics and Computer Science, 13/ 2, 2015.
- [7] E. Hatton. An entire system of arithmetic or arithmetic in all its parts. University of Michigan, 1721.
- [8] N. Herscovics, L. Linchevski. A cognitive gap between arithmetic and algebra. Educational Studies in Mathematics, 1994.
- [9] C. Kieran. Concepts associated with the equal symbol. Educational Studies in Mathematics, 1981.
- [10] Maróthi Gy., Arithmetica, Debrecen, 1782
- [11] K. Stacey, M. McGregor. Learning the algebraic methods of solving problems. Journal of Mathematical Behavior, 18, 2000.
Fülöp Zsolt egyetemi adjunktus
Pedagógusképző Intézet
Károli Gáspár Református Egyetem, Pedagógiai Kar