A kétszintű érettségi vizsgarendszer annak 2005-ös bevezetése óta a magyar közoktatás egyik legstabilabb eleme. A kezdetektől több kutatás középpontjában állt, és bár eleinte voltak, akik kritikával illeték (ld. például Csapó Benő írását a 2008-as Zöld könyvben), az elmúlt időszakban nem merült fel az egész vizsga szerkezetét érintő érdemi változtatásra igény, oktatáspolitikai szándék.
Ezek a megállapítások a matematika tantárgyra is vonatkoznak. Jelen cikk szerzői több írásban, elemzésekben, doktori disszertációban vizsgálták a kétszintű matematika érettségi vizsga különböző elemeit, eredményességét, ezeket a cikk végén egy linkgyűjteményben gyűjtöttük össze. A kutatások alátámasztották az írásbeli vizsga méréselméleti megfelelőségét és a vizsgával való tanári elégedettséget, de jeleztek néhány problémás részterületet is, amelyekről az alábbiakban lesz szó.
Éppen ezek a kutatások, valamint a tantervi követelmények változásának következtében történt ugyan néhány módosítás a vizsgaleírásban és a vizsgakövetelményekben (2017, 2024), de a vizsga alapvető szerkezete nem változott meg az elmúlt 17 év során. (Itt jegyezzük meg, hogy az ezzel ellentétes olvasattal szemben nem változik a középszintű szóbeli vizsgák rendszere 2024-től, az továbbra is csak azok számára lesz kötelező, akik az írásbeli vizsgarészen 12 és 24% között teljesítenek.)
Van azonban néhány probléma, amelyeket nem szabad elhallgatni.
- Kevesen tesznek emelt szintű érettségi vizsgát matematikából.
A kétszintű vizsgarendszer eredeti szándékától eltérően sok olyan egyetemi szak indul, ahol ugyan a tanulmányok eredményes elvégzéséhez szükséges lenne, hogy az oda bekerülő hallgatók emelt szintű érettségi vizsgával rendelkezzenek matematikából, azonban egyfelől az adott szak ezt nem írja elő kötelezően, másfelől a végzős diákok a felvételi pontszámítási rendszer sajátosságai miatt jobban járnak, ha középszintű vizsgát tesznek matematikából. Érdemes a „nagyobb” tárgyak emelt szintű vizsgáinak arányát áttekinteni az adott tárgy összes vizsgáját tekintve, még akkor is, ha tudjuk, hogy ez az egyes tárgyak esetében más-más okokra vezethető vissza: matematika 7,3%, magyar nyelv és irodalom 3,2%, történelem 11,1%, angol nyelv 30,0%, német nyelv 19,6%, biológia 59,2%, fizika 52,3%, kémia 92,0%, informatika 29,3%, földrajz 15,0% (2021 májusi adatok).
- Bizonytalan, hogy milyen ismeretekkel, kompetenciákkal rendelkeznek azok, akik szóbeli vizsgán érik el az elégségeshez szükséges pontszámot.
Nem szeretnénk ebbe a kérdésbe nagyon belemerülni, ezért csak azt jelezzük, hogy azok a diákok (bizonyos években 8-10 000 fő, 2013 óta a vizsgázók átlagosan 12%-a), akik a középszintű írásbelin nem érnek el 25%-ot, pár héttel később már remekül szerepelnek a szóbeli vizsgarészen (mindössze 2-300 diák bukik meg évente a szóbeli vizsgán). Kutatásaink alapján a középszintű szóbeli vizsga matematikából semmiféle méréselméleti alapelvnek nem felel meg. Valószínűsíthetjük, hogy sem a vizsgázók ezen jelentős részhalmaza, sem a középszinten legfeljebb elégséges osztályzatot szerző diákok (akik a teljes érettségiző korosztály 40% körüli részét teszik ki) jelentős része nem éri el azokat az eredményeket, amiket például a Nemzeti alaptanterv megfogalmaz a matematika fejlesztési céljait illetően.
Az egyik nehézséget az a tény okozza, hogy a matematika érettségi eredmények nagy szórást mutatnak, ami különösen akkor látványos, ha a három kötelező érettségi tantárgy eredményeit hasonlítjuk össze. Az alábbi táblázat tartalmazza a matematika, a magyar nyelv és irodalom, valamint a történelem írásbeli százalékos eredmények átlagos szórását a 2018−2022 évek májusi vizsgaidőszakaiban. (Az eredmények szórása meglehetősen stabil, az egyes tárgyakra nagyon jellemző mutató.)

Írásbeli százalékos eredmények átlagos szórása három tárgyból (2018−2022 májusi vizsgaidőszak).
A 2018 és 2022 közötti májusi eredményeken azt is látjuk, hogy míg matematikából középszinten 40% alatt átlagosan a vizsgázók 37%-a teljesít, addig ugyanez az arány magyarból 11%, történelemből pedig 19%. Ugyanakkor a középszinten kimagaslóan jók (tekintsük például a 90% feletti teljesítményt nyújtó diákokat) körében matematikából és magyarból is a diákok 8-10%-a található, míg a történelem esetében ugyanez az arány 5%. Az alábbi diagram mutatja a középszintű eredmények átlagos megoszlását 2018 és 2022 között.
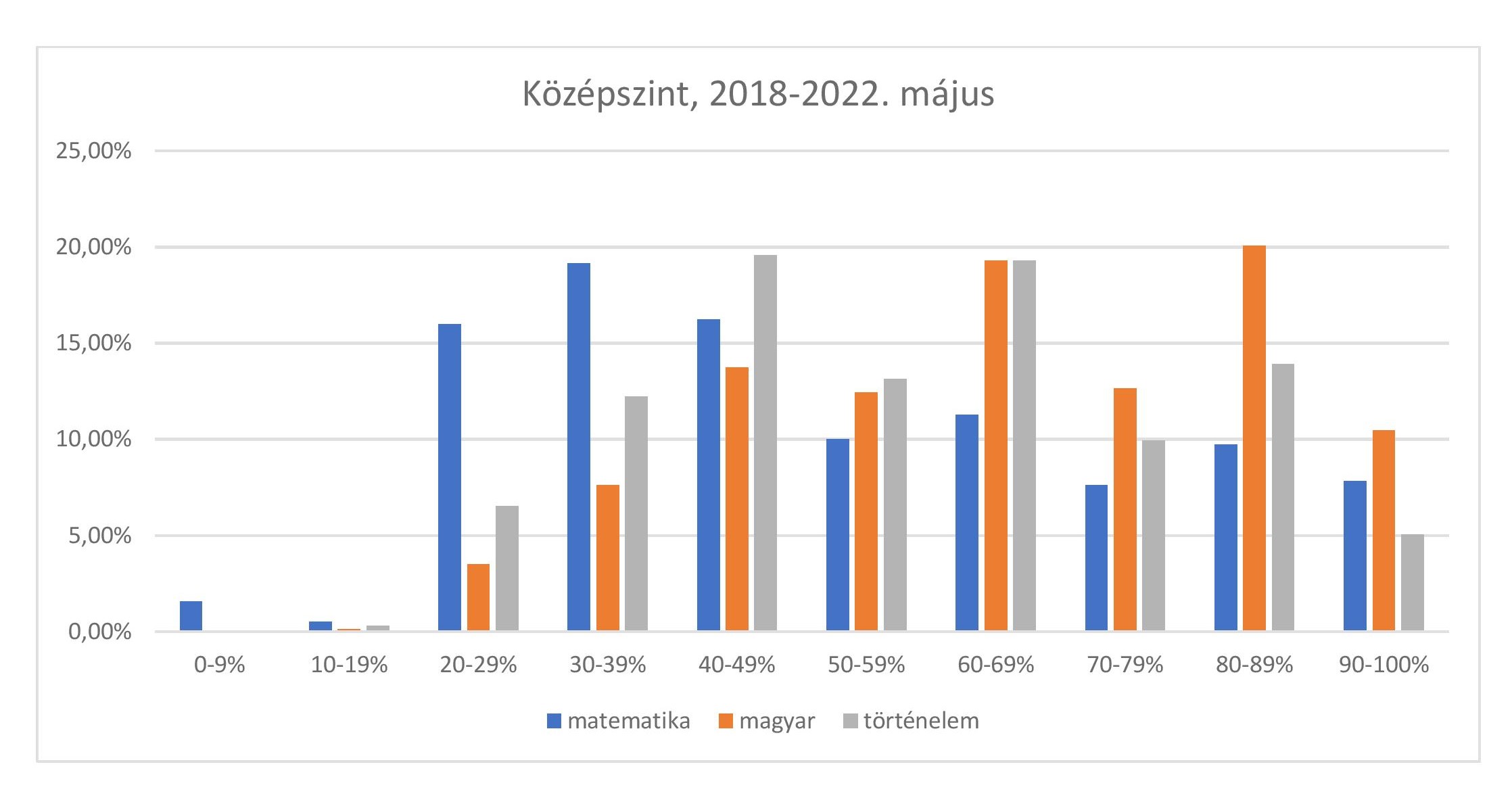
Emelt szinten is hasonló jelenséget láthatunk, itt most az emelt szinten kiválóan (90% feletti eredménnyel) szereplő diákok az elmúlt 5 évet tekintve átlagos arányát emeljük ki: matematikából erre a vizsgázók 15%-a, magyarból és történelemből kb. 5%-a képes. Az alábbi diagramon az is látható, hogy emelt szinten is igaz, hogy matematikából nagyobb a gyengén teljesítők aránya, mint a másik két tárgyból.
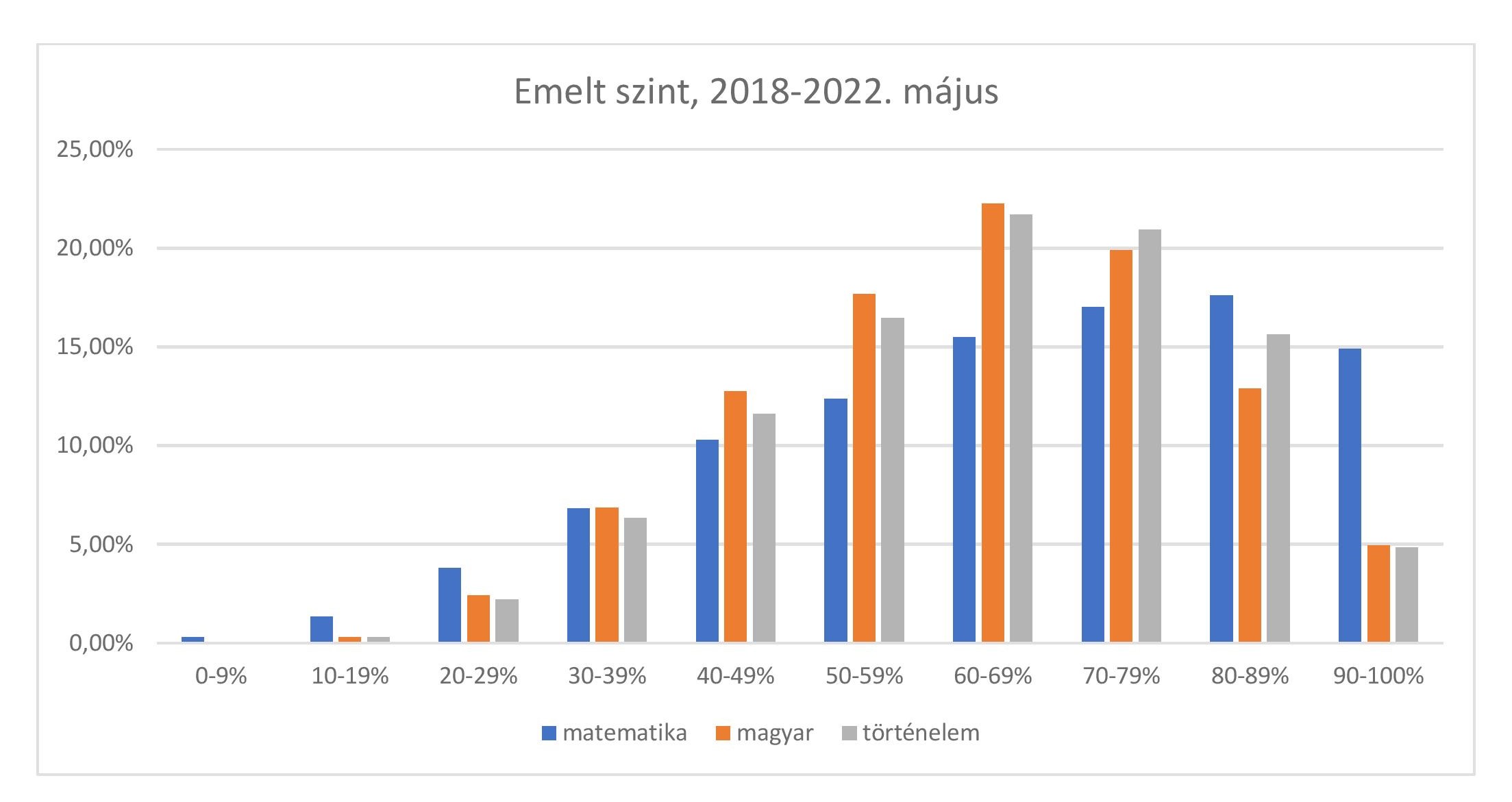
A fentiek alapján tehát azt állapíthatjuk meg, hogy a matematika különleges helyzetben van a közoktatásban, és a (középszintű) matematika érettségi vizsga is nehéz kihívásoknak kell, hogy megfeleljen: egyszerre kell mérnie azokat a diákokat, akik alapvető ismeretekkel is alig rendelkeznek, és azokat, akik – a követelmények megváltozása esetén – sokkal többre is képesek lennének. Ez utóbbiba soroljuk azokat a diákokat, akik jelenleg középszintű érettségit tesznek matematikából, de aztán olyan felsőoktatási intézménybe kerülnek be, ahol igen hamar igen magas elvárásokkal találkoznak matematikából.
Ide tartozó kérdés, hogy az egyes felsőoktatási szakok eredményes elvégzéséhez milyen matematikai ismeretek és kompetenciák szükségesek? Nem tudunk ezzel kapcsolatos átfogó kutatásról, de saját tapasztalataink és másoktól szerzett információk alapján a felsőoktatási szakokat három részre tudjuk osztani:
- az első csoportba azok a szakok tartoznak, ahol szinte semmilyen, a középiskolai ismereteket meghaladó matematikai tudásra nincs szükség. A teljesség igénye nélkül ilyen szakok például: tanítóképzés, művészeti felsőoktatás, bölcsészettudományi szakok egy része, jogi képzés.
- a második csoportba azokat a szakokat sorolhatjuk, ahol – sokszor az oda jelentkező hallgatók számára is meglepő módon – viszonylag komoly matematikai tanulmányok zajlanak, de ezek inkább gyakorlati jellegű kurzusok. Ezeken a szakokon elsősorban az alkalmazásra helyezik a hangsúlyt, kevés elméleti ismeretet kérnek számon a hallgatóktól. Ilyennek tekinthetjük például a szociológia és pszichológia szakok statisztika tárgyait, a gazdasági szakok analízis, algebra, valószínűségszámítási kurzusait. Ezeknek a szakoknak egy része tulajdonképpen elő kellene, hogy írja a kötelező emelt szintű érettségi vizsgát matematikából, de nem teszi.
- a harmadik csoportba pedig azok a szakok tartoznak, ahol komoly és elméletileg is megalapozott matematikaoktatás zajlik. Ilyen természetesen a matematikus szak, de ide sorolhatjuk a mérnöki tanulmányokat, illetve egyéb természettudományi alapszakokat, az elméleti jellegű gazdasági felsőoktatást, vagy akár az informatikus képzést.
Megoldás lenne, ha több, a második csoportba tartozó felsőoktatási szak írná elő kötelezően az emelt szintű érettségi vizsga letételét matematikából, de az elmúlt évtized tapasztalatai alapján erre nem érdemes várni. Sőt, a legújabb hírek szerint pont ezzel ellentétes irányú folyamat várható.
Egy másik megoldás lehetne – a többszintű érettségi vizsgarendszer eredeti koncepciójának megfelelően – egy harmadik, ún. alapszintű vizsga bevezetése. Ez azoknak a diákoknak jelentene lehetőséget a közoktatásbeli tanulmányaik lezárására, akik érettségi vizsgabizonyítványt szeretnének szerezni, de nem kívánnak a felsőoktatásban továbbtanulni. Nem tudunk olyan szándékról, ami ebbe az irányba terelné az érettségi vizsga rendszerét. Már csak azért sem, mert a többi tárgy valószínűleg kevésbé küszködik a fenti problémákkal.
Így akkor nem marad más lehetőség a matematika számára: a jelenlegi körülmények mentén kell megoldást találni a problémákra. Egy ilyen lehetséges megoldást vázolunk az alábbiakban. Hangsúlyozzuk, hogy nem foglalkozunk jogi, közigazgatási, szervezési, anyagi kérdésekkel. Arra vagyunk kíváncsiak, hogy a matematikatanári társadalom mit gondol az alábbi javaslatról szakmai, módszertani szempontból.
A javaslat lényege: kétféle matematika érettségi vizsgát lehessen tenni, az egyszerűség kedvéért nevezzük ezeket most Matematika I és Matematika II tárgyaknak. Mindenkinek kötelező lenne valamelyik matematika tárgyból érettségi vizsgát tenni.
A Matematika I tárgyból csak középszinten lehetne vizsgázni. Ezt a vizsgát azok a diákok választanák, akik vagy nem akarnak továbbtanulni, de szeretnének érettségi vizsgát szerezni, vagy olyan szakon szeretnének továbbtanulni, ahol komolyabb matematikai ismeretekre nincs szükségük a hallgatóknak. Ennek a tárgynak a vizsgakövetelményei értelemszerűen némileg alacsonyabbak lennének, mint a jelenlegi középszintű követelmények matematikából, a fő hangsúly a hétköznapi ismereteken, a matematika alkalmazásán lenne (százalékszámítás, terület, kerület, felszín, térfogat, statisztikai ismeretek stb.). A követelmények ilyesfajta átalakítása együtt járhatna azzal, hogy nem lenne menekülő út a szóbeli; aki ezen az írásbeli vizsgán nem teljesíti ezeket az alapvető követelményeket, az ne szerezzen érettségi bizonyítványt, amíg ezeket a hiányosságokat nem pótolja.
A Matematika II tárgyból lehetne középszinten és emelt szinten is vizsgázni. A középszintű vizsga lehetne a jelenleginél kicsit nehezebb, számon kérhetne több ismeretet, szerepelhetnének benne a jelenleginél kicsit összetettebb feladatok. Nem kellene ugyanis attól tartani, hogy emiatt nagyon sokan nem tudnak érettségi vizsgát tenni, hiszen nekik ott a Matematika I, ugyanakkor a némileg több matematikai felkészültséget igénylő felsőoktatási szakra (ld. fenti második csoport) készülő diákokat a jelenleginél nagyobb (de nem túl nagy) kihívás elé állítaná.
A Matematika II tárgy emelt szintű vizsgájának követelménye és szerkezete megegyezhetne a jelenlegi emelt szintű matematika vizsgával. Bár vannak olyan vélemények, hogy ezen is lehetne nehezíteni, visszahozni a régi matematika felvételik 7-8. feladatainak nehézségét, jelen cikk szerzői ezt nem támogatják. Az érettségi vizsga célja nem a tehetséges diákok felismerése, rangsorolása – erre a célra például a rengeteg verseny kiválóan alkalmas eszköz.
Fontos kiemelni, hogy ebben a cikkben nem foglalkozunk tantervi kérdésekkel. Messzire vezetne (bár nemzetközi példa akad rá), ha nem csak a vizsga válna ilyen módon ketté, hanem a matematika tanítása is, tantervvel, tankönyvvel együtt. Az elképzelésünk most csak addig terjed, hogy a matematika tanítása ugyanúgy, ugyanolyan tartalommal zajlik, mint eddig, csak az utolsó év februárjában az érettségi előtt álló diák – a továbbtanulási elképzelései ismeretében – eldönti, hogy számára melyik matematika tárgy melyik vizsgája a megfelelő. Természetesen arra is lenne lehetőség, hogy ha valaki Matematika I tárgyból tesz vizsgát, azt később kiegészítse valamelyik Matematika II vizsga letételével, ha a továbbtanulási szándékai később megváltoznának. És biztosan felmerül sok apró technikai kérdés, de újra hangsúlyozzuk, hogy ezekkel egyelőre nem kívánunk foglalkozni, amíg nem látjuk a kollégák véleményét, támogatását, illetve ellenkezését a javaslat alapvető irányaival kapcsolatosan.
A javaslat várható előnyei:
- A választott tárgy (és szint) ismeretében pontosabb képe lehet arról a felsőoktatásnak, hogy az érettségi bizonyítvány birtokában milyen matematikai ismeretekre, kompetenciákra számíthatunk a diákoktól.
- Azok számára, akik nem akarnak sokat a matematikától (be akarják fejezni a középiskolai tanulmányaikat, olyan szakon tanulnak tovább, ahol nincs rá nagyon szükség) több sikerélményt adhat egy – a jelenleginél várhatóan jobb érdemjeggyel zárt – Matematika I érettségi. Ez a javulás akár az egész matematika tárgy „mumus” jellegét csökkentheti.
- Azok számára, akik matematikát igénylő, de csak középszintű vizsgát előíró szakon tanulnának tovább, a jelenleginél kicsit magasabban lenne a mérce. Ezt a vizsgát ők várhatóan különösebb nehézség nélkül tudnának teljesíteni, hogy aztán a felsőoktatásban jobban megállják a helyüket, alacsonyabb lemorzsolódást eredményezve.
Nehéz megbecsülni, hogy a javaslat életbe lépése esetén milyen arányban választanák a diákok az egyes tárgyakat/szinteket. Miután az érettségi vizsgát tevők kb. 60%-a tanul tovább a felsőoktatásban, és a továbbtanulók körülbelül 10-15%-a jelentkezik a korábban említett első csoportba tartozó szakra, így a Matematika I tárgyra várhatóan a vizsgázók 50%-a jelentkezne. Ez hozzávetőlegesen megegyezik azoknak az arányával, akik a jelenlegi vizsgán középszinten 50% alatt teljesítenek.
Nem tudjuk, hogy az itt ismertetett javaslatunk megvalósulásának van-e bármilyen esélye. Úgy látjuk, hogy ha ez bekövetkezne, az jó hatással lehetne a matematika tanításának helyzetére a közoktatásban és a felsőoktatásban egyaránt. Ha az általunk erről a kérdésről kezdeményezett vita során nem merül fel komoly ellenérv vagy megalapozottan határozott ellenállás a kollégák részéről, akkor érdemesnek látjuk a döntéshozók felé is jelezni a felvetést, hogy az érettségi vizsga soron következő felülvizsgálata, átalakítása során megfontolhassák mindezeket.
Kérjük, vegyen részt Ön is a vitában, az Érintő Facebook-oldalán a témához kapcsolódó megjegyzésével, vagy hosszabb véleményét küldje el a Ez az e-mail-cím a szpemrobotok elleni védelem alatt áll. Megtekintéséhez engedélyeznie kell a JavaScript használatát. email-címre.
Csapodi Csaba, Koncz Levente
Irodalom
Csapó Benő, 2008. A közoktatás második szakasza és az érettségi vizsga, in: Zöld könyv a magyar közoktatás megújításáért 2008, szerk.: Fazekas Károly Köllő János Varga Júlia https://mek.oszk.hu/08200/08222/08222.pdf
Az adatok forrása
https://www.oktatas.hu/kozneveles/erettsegi/statisztikak_vizsgaeredmenyek
Linkgyűjtemény az érettségi vizsgával kapcsolatos írásokhoz
A 2012. május-júniusi érettségi feladatsor és az egyes feladatok mérésmetodikai vizsgálata
http://www.oktatas.hu/kozneveles/projektek/tamop318_minosegfejl/projekthirek/erettsegi_vizsgafeladatok_elemzese
http://www.oktatas.hu/pub_bin/dload/unios_projektek/tamop318/meresmetodika/Matematika.pdf
Érettségi vizsgatárgyak elemzése 2009-2012. tavaszi vizsgaidőszakok
http://www.oktatas.hu/kozneveles/projektek/tamop318_minosegfejl/projekthirek/erettsegi_vizsgatargyak_elemzese
http://www.oktatas.hu/pub_bin/dload/unios_projektek/tamop318/erettsegi_vizsgatargyak_elemzese/matematika.pdf
A kétszintű érettségi rendszerrel kapcsolatos változtatási igények felmérése a gyakorlati tapasztalatok alapján
http://www.oktatas.hu/kozneveles/projektek/tamop318_minosegfejl/projekthirek/ketszintu_erettsegi_vizsgarendszer_tanari_tapasztalatok
http://www.oktatas.hu/pub_bin/dload/unios_projektek/tamop318/erettsegi_konferencia2014/vitaindito_matematika.pptx
A közép- és emelt szintű értékelési skálák összehasonlítása
http://www.oktatas.hu/kozneveles/projektek/tamop318_minosegfejl/projekthirek/erettsegi_ertekelesi_skalak_elemzese
http://www.oktatas.hu/pub_bin/dload/unios_projektek/tamop318/ertekelesi_skalak_osszehasonlitasa/ertekelesi_skalak_matematika.pdf
Csaba Csapodi and Levente Koncz: The efficiency of written final exam questions in mathematics based on voluntary data reports, 2012–2015, Teaching Mathematics and Computer Science, 2016/14 p63-81)
http://tmcs.math.unideb.hu/load_doc.php?p=306&t=abs
A matematika érettségi vizsga elemzése 2005-2015 (Csapodi Csaba doktori értekezése)
https://dea.lib.unideb.hu/dea/handle/2437/236563
Előadások a Rátz László Vándorgyűlésen:
http://rlv.berzsenyi.hu/2015/Koncz_Csapodi.ppsx?attredirects=0&d=1 (2015)
http://rlv.berzsenyi.hu/2016/Eredmenyesseg%20es%20sz%D0%B0mologep-haszn%D0%B0lat%20az%20Erettsegi%20vizsg%D0%B0n.ppsx?attredirects=0&d=1 (2016)
http://rlv.berzsenyi.hu/2017/Csapodi-Koncz_Matematikaerettsegi_RLV17_KL.ppsx (2017)
https://www.bolyai.hu/files/RLV_2018_Csapodi_Koncz.ppsx (2018)
https://www.bolyai.hu/files/RLV_2019_CsapodiCs-KonczL_Az%20erettsegirol%20erdekesen.ppsx (2019)
https://www.bolyai.hu/files/RLV_2021_eloadas_Koncz_Csapodi.ppsx (2021)
https://www.bolyai.hu/files/RLV_2022_eloadas_KonczL_vegleges.pps (2022)









