A cikksorozat első részében foglalkoztunk többek között az exponenciális függvénnyel és a logaritmikus skálával. Ebben a részben ezeket az ismereteket is felhasználva a Covid-járvány kapcsán sokszor látott görbékről lesz szó. A hivatkozásokat követve az eredeti oldalakon sok grafikon paraméterezhető változata is megtalálható, érdemes ezekkel kísérletezni.
Járványgörbék1
A kumulált adatokból készített járványgörbe2
Az alábbi levezetés a 3Blue1Brown videója alapján készül.
Azt fogjuk megadni, hogy adott idő elteltével hányan lesznek összesen a populációban, akik már megfertőződtek a vírussal. (Az összes megfertőzöttet mutató görbe monoton növő, hiszen az újonnan felfedezett esetek hozzáadódnak a már meglévőkhöz.)
Legyen 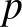 ezúttal a megfertőződés valószínűsége, azaz a fertőzés átadásának esélye. Induljunk
ezúttal a megfertőződés valószínűsége, azaz a fertőzés átadásának esélye. Induljunk 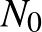 fertőző személlyel. Tegyük fel, hogy mindegyikük minden nap átlagosan
fertőző személlyel. Tegyük fel, hogy mindegyikük minden nap átlagosan 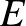 fogékony emberrel találkozik. (A modell itt már elrugaszkodik a valóságtól, a pontosabb becslésre nem is ezt, hanem egy ennél jóval bonyolultabb modellt használnak.) Az
fogékony emberrel találkozik. (A modell itt már elrugaszkodik a valóságtól, a pontosabb becslésre nem is ezt, hanem egy ennél jóval bonyolultabb modellt használnak.) Az 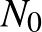 ember mindegyike tehát átlagosan
ember mindegyike tehát átlagosan 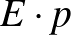 személyt fertőz meg.
személyt fertőz meg.
Egy nap múlva azoknak a száma, akik már megfertőződtek: 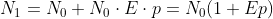 .
.
Nézzük meg, mi lesz a helyzet 2 nap múlva: 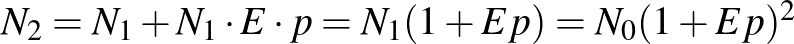 .
.
Hasonlóan folytatva a gondolatmenetet, megkapjuk, hogy a 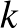 -adik napon az összes megfertőződött számát az
-adik napon az összes megfertőződött számát az 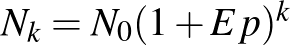 összefüggés adja meg.
összefüggés adja meg.
Ebben a képletben az 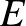 és a
és a 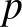 a két változó érték, és a végeredmény nagyon érzékeny az
a két változó érték, és a végeredmény nagyon érzékeny az 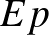 szorzatra. Számoljunk utána. Kezdjünk
szorzatra. Számoljunk utána. Kezdjünk 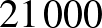 fertőzöttel (
fertőzöttel (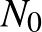 ), és vizsgáljunk körülbelül 2 hónapot (61 nap). Az egyik esetben
), és vizsgáljunk körülbelül 2 hónapot (61 nap). Az egyik esetben 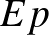 értéke
értéke 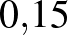 , a másik esetben
, a másik esetben 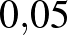 legyen. Az
legyen. Az 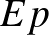 szorzat
szorzat 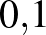 -del való csökkentése milyen arányú változást eredményez a 61 nap alatt megbetegedettek számában?
-del való csökkentése milyen arányú változást eredményez a 61 nap alatt megbetegedettek számában?
Megoldás:
1. eset: 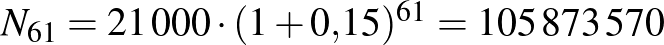 .
.
2. eset: 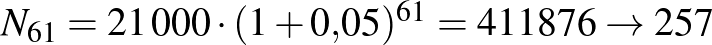 -szer ennyi fertőzött lett az 1. esetben.
-szer ennyi fertőzött lett az 1. esetben.
Ahhoz tehát, hogy a járvány lassuljon, az 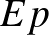 szorzat csökkenésére van szükség. Ez előbb-utóbb beavatkozás nélkül is lecsökken, hiszen minél többen esnek át a fertőzésen, annál kevesebb olyan emberrel tud találkozni a fertőzött, aki még nem volt beteg3. Emiatt a görbe alakja ehhez hasonlóan fog kinézni4:
szorzat csökkenésére van szükség. Ez előbb-utóbb beavatkozás nélkül is lecsökken, hiszen minél többen esnek át a fertőzésen, annál kevesebb olyan emberrel tud találkozni a fertőzött, aki még nem volt beteg3. Emiatt a görbe alakja ehhez hasonlóan fog kinézni4:
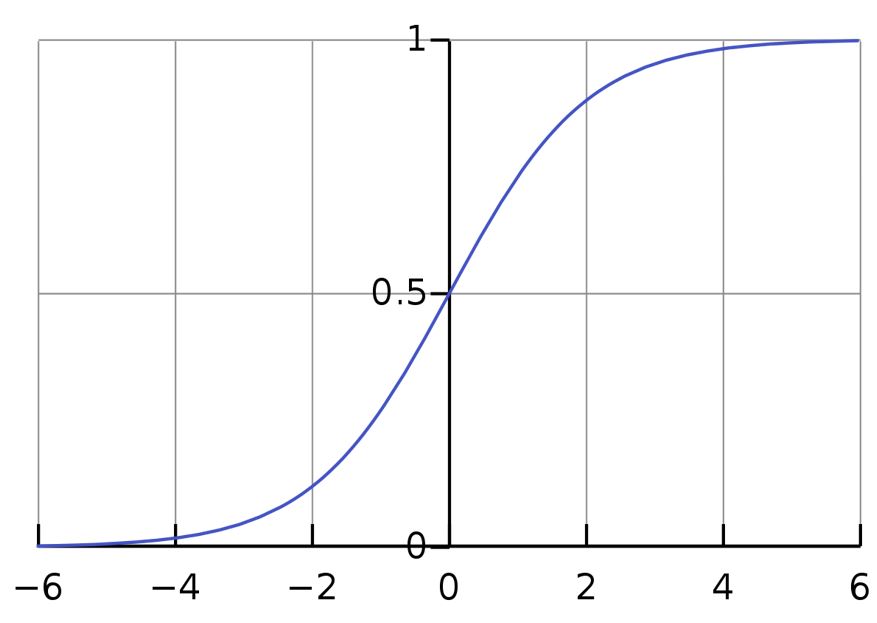
Egy egy szigmoid típusú görbe. Az S-betű alakjára hasonlító folytonos függvényeket nevezzük szigmoid függvényeknek, közülük az 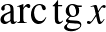 függvénnyel esetleg találkozhattak a diákok matematika órán. A járványgörbék néha hasonlítanak a szigmoid görbékre, de lényeges különbség közöttük az, hogy a járványgörbék nem szimmetrikusak. (Később a valósághűbb SIR-modellnél ezt látni is fogjuk.)
függvénnyel esetleg találkozhattak a diákok matematika órán. A járványgörbék néha hasonlítanak a szigmoid görbékre, de lényeges különbség közöttük az, hogy a járványgörbék nem szimmetrikusak. (Később a valósághűbb SIR-modellnél ezt látni is fogjuk.)
Ha meg szeretnénk akadályozni, hogy a járvány kontrollálatlanul söpörjön végig a populáción, akkor az 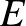 és a
és a 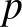 értékét kell csökkenteni. Gondoljuk végig, hogy a két változót milyen beavatkozásokkal lehetne csökkenteni.
értékét kell csökkenteni. Gondoljuk végig, hogy a két változót milyen beavatkozásokkal lehetne csökkenteni.
| E | p |
 a kontaktszámok csökkentését célzó intézkedések a kontaktszámok csökkentését célzó intézkedések  a fertőzöttek elkülönítését célzó intézkedések a fertőzöttek elkülönítését célzó intézkedések  védőoltás védőoltás |
 A megfertőződés valószínűségének csökkentését célzó intézkedések, tevékenységek a vírus terjedési tulajdonságaitól függnek. Koronavírus esetén ezek például a maszkviselés, a gyakori kézmosás vagy fertőtlenítés, szellőztetés stb. A megfertőződés valószínűségének csökkentését célzó intézkedések, tevékenységek a vírus terjedési tulajdonságaitól függnek. Koronavírus esetén ezek például a maszkviselés, a gyakori kézmosás vagy fertőtlenítés, szellőztetés stb. |
Egy járvány elindulásakor az összes fertőzöttet és a napi új fertőzéseket mutató görbe alakja is exponenciális. Ahogy az előbb láttuk, elérkezik a járvány lefolyása során az a pont, amikor a fertőzés sebessége csökkenni kezd.
Az új fertőzöttek számát mutató járványgörbe alakja
Az alábbi diagram az ausztráliai esetszámokat mutatja5. Érdekessége, hogy ezen egyszerre láthatók a napi esetszámok és az adott nappal bezárólag regisztrált fertőzések száma:
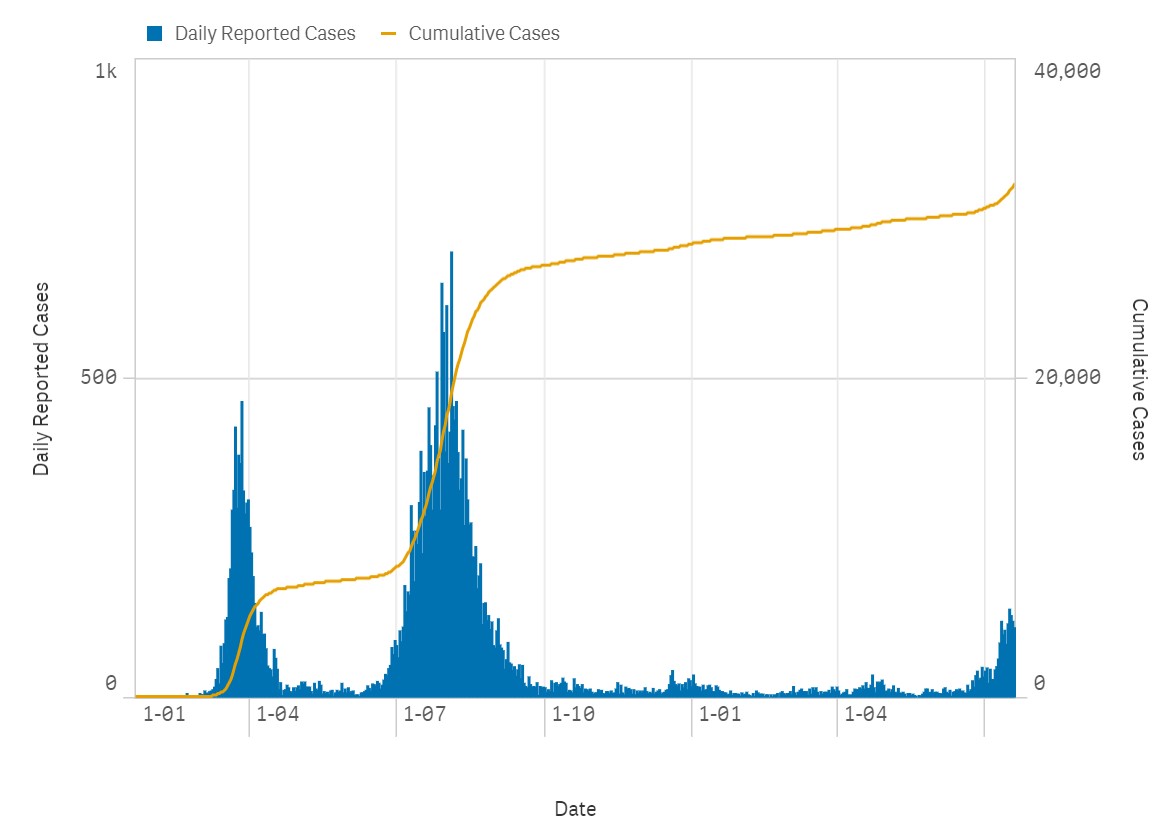
A napi új esetszámokat a kék oszlopdiagram mutatja, a hozzá tartozó értéktengely a bal oldalon található. Az adott napig bekövetkezett összes ismert fertőzés a korábban már vizsgált sárga színű vonaldiagramon látszik, ennek értéktengelye a jobb oldalon látható. Észrevehető a kapcsolat a két görbe között: amikor az effektív reprodukciós szám csökkenni kezd (adott napon kevesebb fertőzés van, mint előtte), akkor kezd el a csökkenni a sárga grafikon növekedési üteme is.
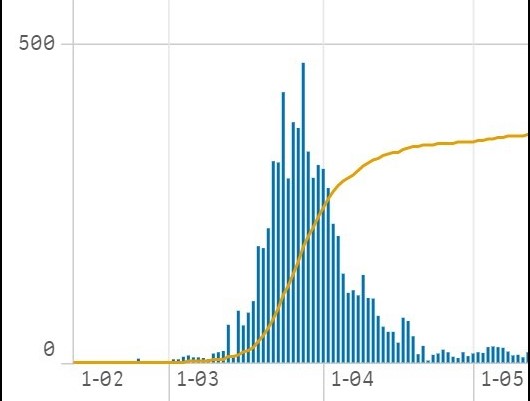
Emeljük ki a fenti grafikonból azt a részt, ami az első lecsengésig tart, vagyis amíg a sárga grafikon befutja a már látott S-alakot. Láthatjuk, hogy a másik grafikon ezalatt egy harangszerű alakot ír le.
Az ausztrál görbéhez hasonló, két hullámos járványgörbéje volt a torontói SARS-járványnak 2003-ban6:
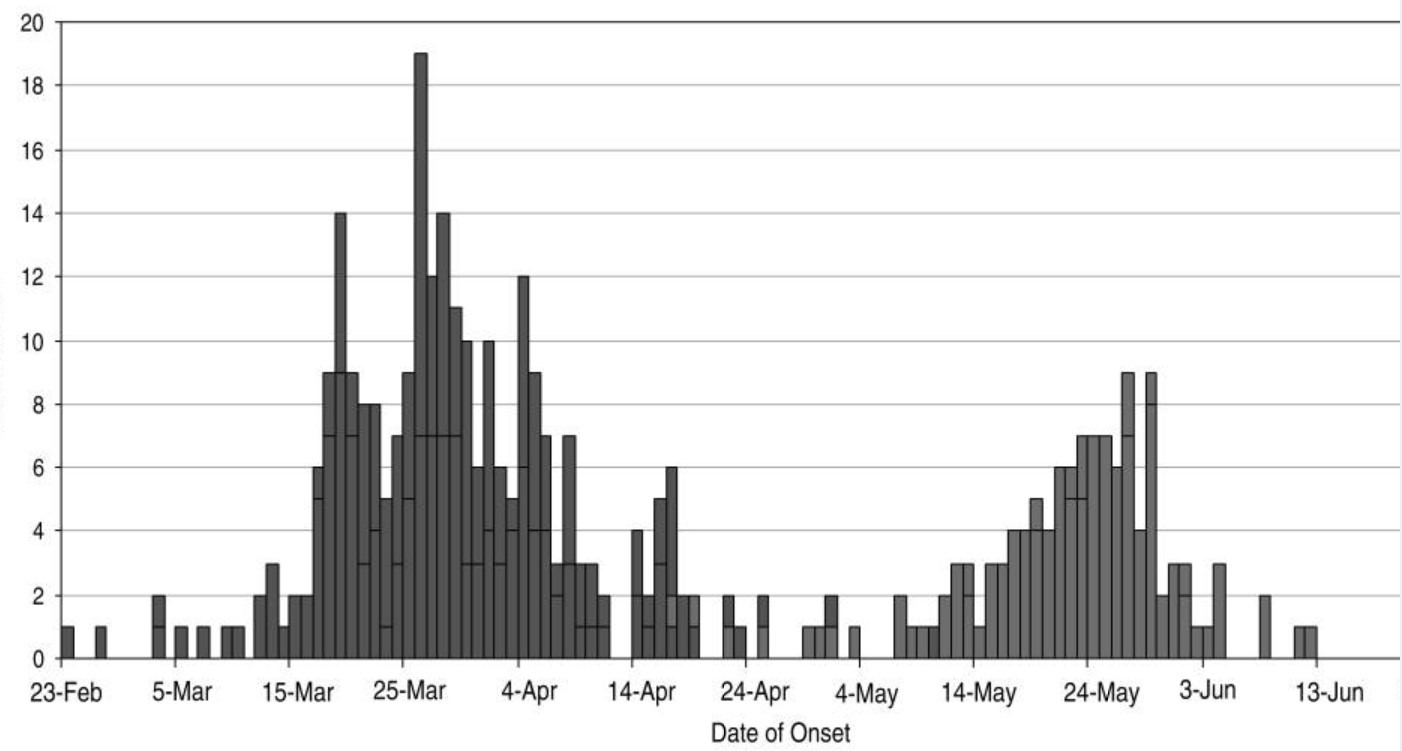
A koronavírussal kapcsolatban az aktív eseteket mutató görbe futott be nagyobb karriert a médiában. Aktív esetnek számít mindenki, akinél tesztekkel igazolhatóan tart a betegség.
Tegyük egymás mellé az új esetek és az aktív esetek magyarországi görbéjét!7 Láthatjuk a hasonlóságot a két görbe alakja között:
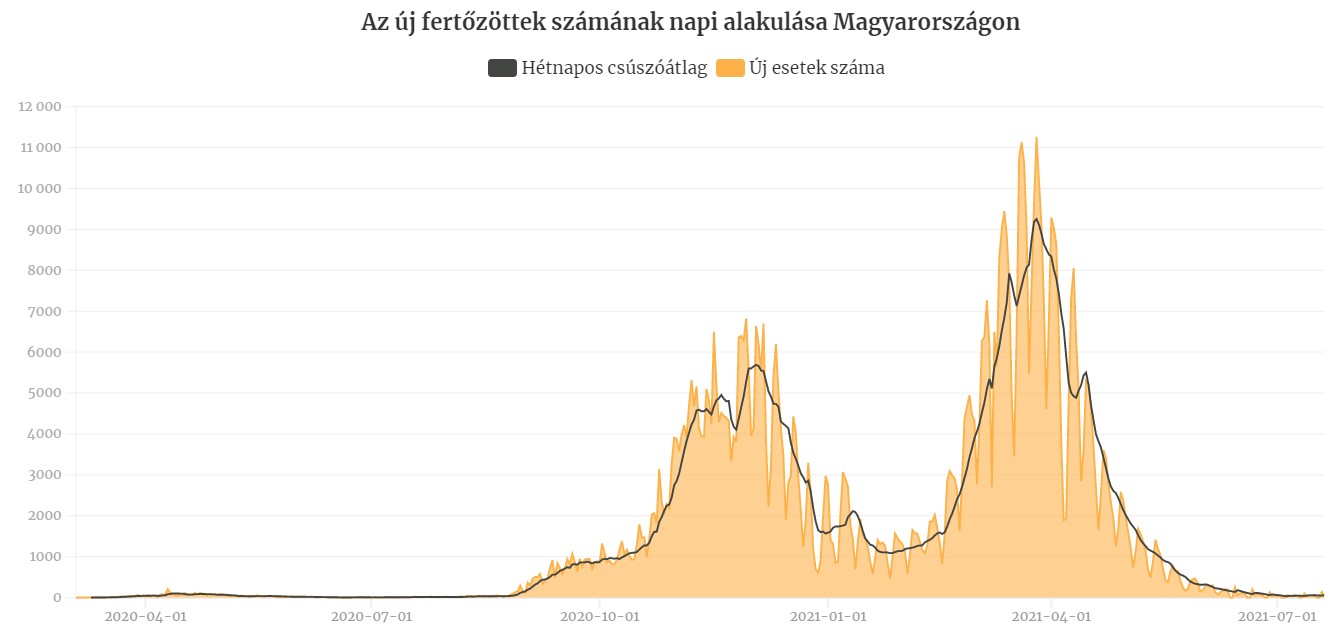
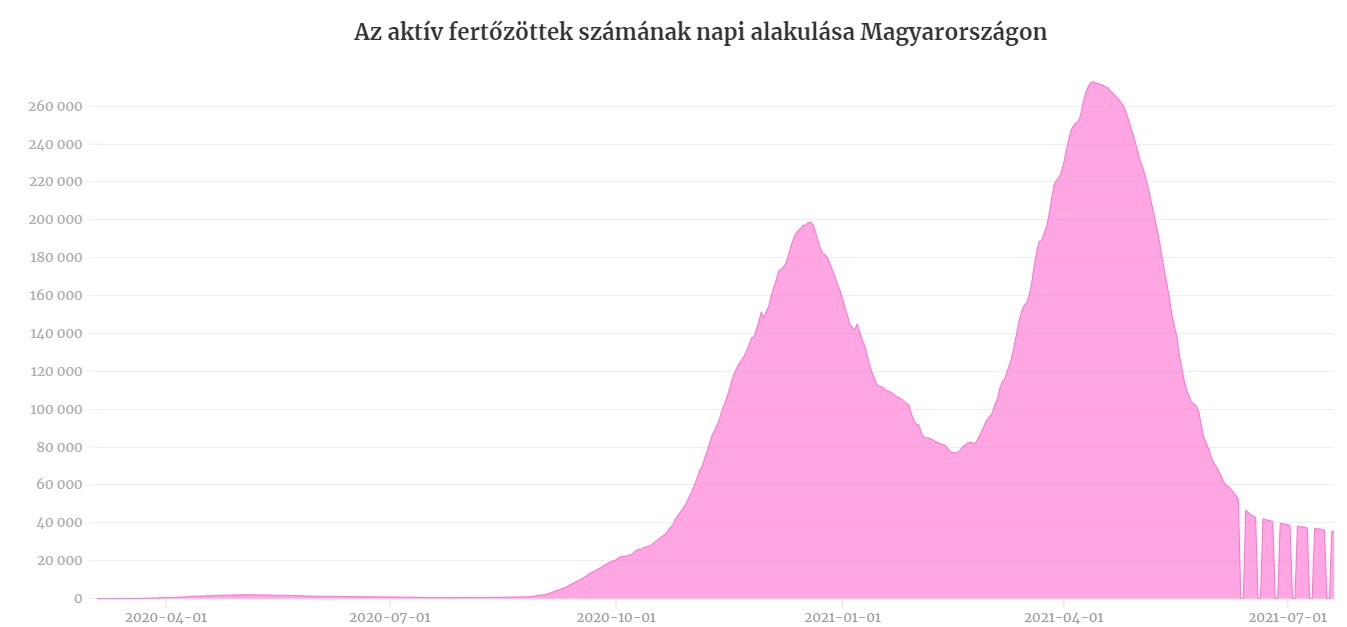
Bizonyára sokan találkoztak a „lapítsuk el a görbét” felhívással. Ez az aktív esetek görbéjén a „harang” magasságának a csökkentésére vonatkozott. A „flattening the curve” avagy „laposítsuk el a görbét” híressé vált grafikonja:
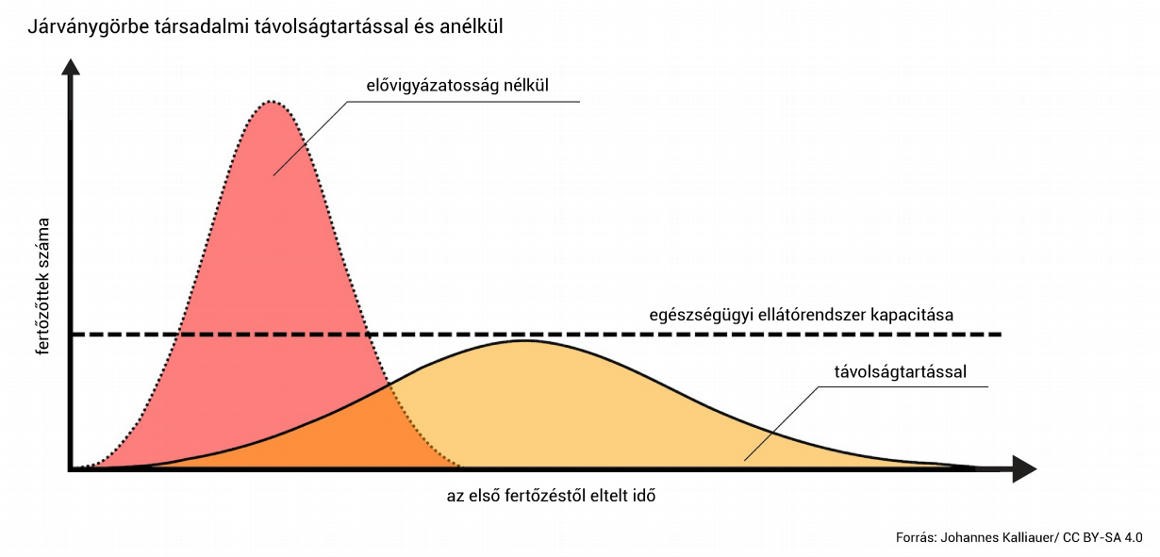
Röst Gergely matematikus véleménye az ábráról: „Mindenki első pillantásra látja a két görbe közötti különbséget: az egyik jóval csúcsosabb, a másik szinte teljesen lapos, és van egy vízszintes vonal az ábrán, amely az egészségügyi kapacitást mutatja. Több szempontból kritizálták ezt az ábrázolást: az egészségügyi kapacitást nem vízszintes vonallal kéne jelölni, hiszen a legtöbb országban bővítettek a kapacitáson; kritizálták az arányokat is, hiszen az ábrán a csúcsosabb görbe nagyjából kétszer olyan magasra megy, mint a másik, míg a legrosszabb forgatókönyvek alapján legalább tízszer magasabb lenne. A pontatlanságok ellenére ez a jó kompromisszum kategóriába tartozik, mert a lényeget mindenki számára befogadható módon közvetíti.”8
A korlátozó intézkedések és a görbe „lapulása” közötti összefüggést jól szemlélteti a Washington Post által közölt szimuláció, melyet bárki lefuttathat. (Magyar nyelven az alapblog.hu-n olvasható összefoglaló a Washington Post cikkéről.) A korlátozások 4 fokozatához tartozó grafikonokon a narancssárga „harang” magassága a korlátozások mértékének megfelelően változik:

Történelmi példák is vannak arra, hogy a szociális távolságtartás járvány esetén hatásos védekezési módszer. A g7.hu cikkét idézzük.
Az USA-ban megvalósulhattak olyan kutatások, amelyek egy száz évvel ezelőtti járványra (a spanyolnátha-járványra) adott intézményi reakciók hatásait vizsgálták a járvány lefolyására és halálozási rátájára.
Az amerikai Nemzeti Tudományos Akadémia folyóiratában 2007-ben megjelent tanulmány fő üzenete szerint a járványra adott nem gyógyszerészeti beavatkozások és ezen belül is az időben bevezetett, a társadalmi távolságtartást eredményező megoldások (tömegrendezvények betiltása, iskolák, templomok bezárása stb.) nélkülözhetetlen szerepet játszottak abban, hogy mérsékelni lehetett a spanyolnátha-járvány hatását, csökkenteni lehetett a járvány halálozási rátáját.
A tanulmányban a szerzők két város, Philadelphia és St. Louis vezetésének az 1918-as spanyolnátha-járványra adott válaszait hasonlították össze. Míg Philadelphiában a politikusok késlekedve, csak két héttel az első esetek megjelenése után mertek döntést hozni a tömegrendezvények, összejövetelek betiltásáról, az iskolák, a templomok és a színházak bezárásáról, addig St. Louisban mindjárt az első esetek megjelenése után pár nappal meghozták ezeket a döntéseket. Ez a különbség megdöbbentő hatást gyakorolt a két városban a járvány halálozási rátájára. Philadelphiában lakosságarányosan sokkal többen haltak meg, mint St. Louisban. Míg Philadelpiában a járvány csúcspontján, amikor a legtöbben haltak meg (1918. október 19-én) 100 ezer lakosra vetítve 257 haláleset történt, addig St. Louisban a csúcs december 14-én volt 31 halottal 100 ezer lakosra vetítve.
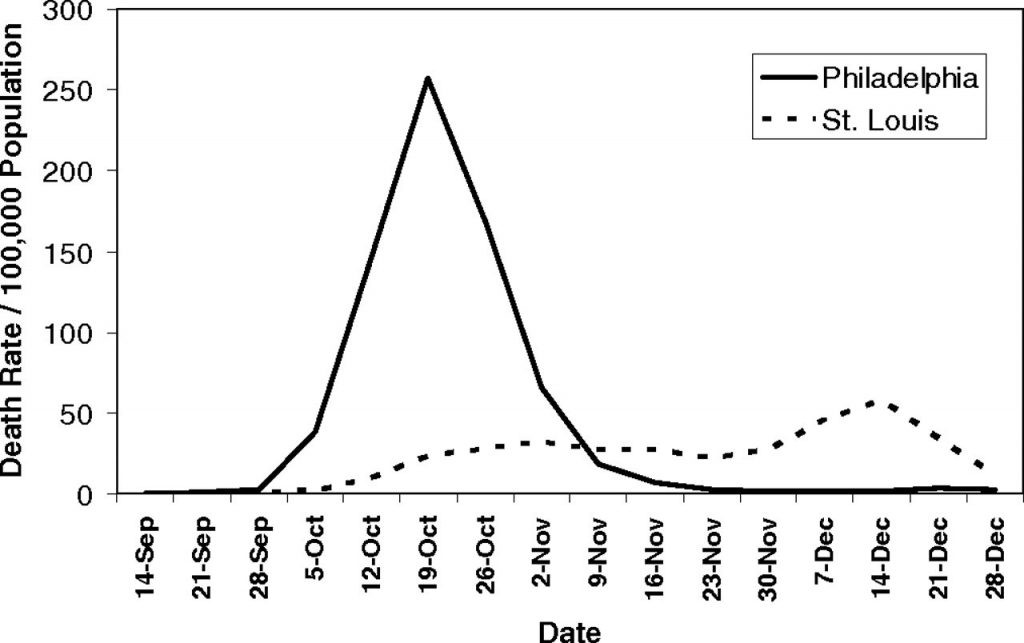
De nemcsak a halálozási ráták csúcsaiban, hanem a halottak számában is hatalmas különbségek mutatkoztak. Míg Philadelphiában 100 ezer lakosra vetítve 719-en haltak meg a vizsgált időszak alatt, addig St. Louisban feleannyian, 347-en. Más vizsgálatok, amelyek már nemcsak két várost, hanem az USA 43 nagyobb városát vizsgálták, egyértelmű és szignifikáns összefüggést találtak a társadalmi életet korlátozó beavatkozások három fajtája (iskolák bezárása; közösségi rendezvények betiltása; karantén elrendelése) és a spanyolnátha-járványban a halálozási ráták alakulása között.
A fenti tanulmányok eredményei alapján tehát azt lehet látni, hogy azokban a városokban, amelyekben korábban vezették be a társadalmi életet korlátozó intézkedéseket, ott később ért a csúcsra a járvány, kisebb volt ez a csúcs, és végül alacsonyabb mortalitási rátával tudtak túl lenni a járványon.
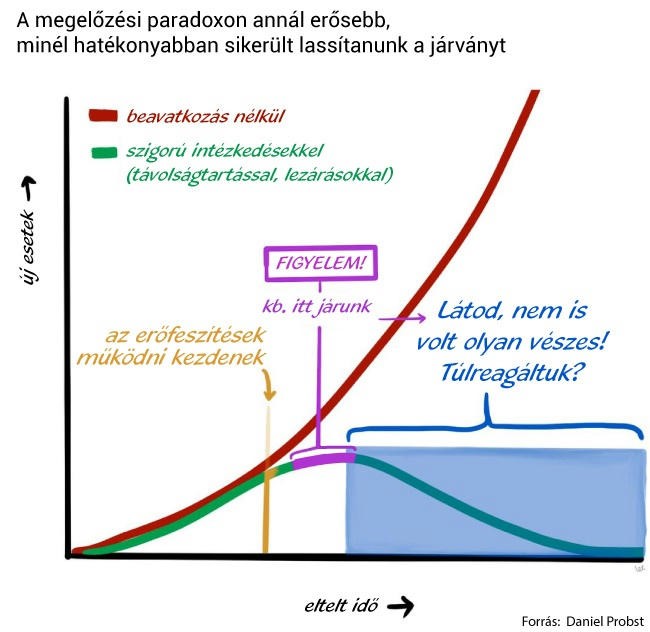 A görbe sikeres lapításának hátulütője az úgynevezett megelőzési paradoxon. Ahol viszonylag gyorsan sikerült megállítani a vírus terjedését és lassítani a járványt, egyre többen vélik úgy, hogy a hatóságok túlreagálták a járványhelyzetet, nő a gazdasági és politikai nyomás az élet normalizálására, és lesznek, akik sokkal lazábban veszik majd a vírushelyzetet, megágyazva ezzel egy következő hullámnak.9 (A szigorítások és az enyhítések értékelésénél azt is figyelembe kell venni, hogy a járványgörbén csak késve mutatkoznak a bekövetkező hatások.)
A görbe sikeres lapításának hátulütője az úgynevezett megelőzési paradoxon. Ahol viszonylag gyorsan sikerült megállítani a vírus terjedését és lassítani a járványt, egyre többen vélik úgy, hogy a hatóságok túlreagálták a járványhelyzetet, nő a gazdasági és politikai nyomás az élet normalizálására, és lesznek, akik sokkal lazábban veszik majd a vírushelyzetet, megágyazva ezzel egy következő hullámnak.9 (A szigorítások és az enyhítések értékelésénél azt is figyelembe kell venni, hogy a járványgörbén csak késve mutatkoznak a bekövetkező hatások.)
A koronavírussal kapcsolatos további görbék elemzése
Sok helyen találunk a koronavírussal kapcsolatban jól elemezhető grafikonokat. Hármat külön is kiemeltem lejjebb, de számtalan egyéb grafikont találhatunk az interneten. Kifejezetten a koronavírussal kapcsolatos magyar adatokat dolgozza fel látványos, informatív formában az Átló Team. Az angol nyelvű oldalak közül a Worldometer és az OurWorldinData a legváltozatosabb területek, témák statisztikai adatait vizualizálja, a grafikonok többsége ráadásul a felhasználók által paraméterezhető. Megemlíteném még a Financial Times „koronavírus-idővonalát”, amely 2020 októberéig foglalja össze nagy vonalakban a világjárvánnyal kapcsolatos statisztikákat látványos infógrafikákkal illusztrálva.
Mozgóátlagot mutató grafikonok
Több grafikonon megjelenik a mozgóátlag vagy csúszóátlag. Feljebb láthattunk egy ábrát a magyar adatokról a fertőzöttek napi alakulásával és a hétnapos csúszóátlaggal (Az új fertőzöttek számának napi alakulása Magyarországon címmel). A mozgóátlag a kiugrások „elsimításával” világosabban mutatja a trendeket. A grafikonon látható hétnapos csúszóátlag értékét az adott napi és az előző 6 napi értékek számtani közepeként határozzuk meg.
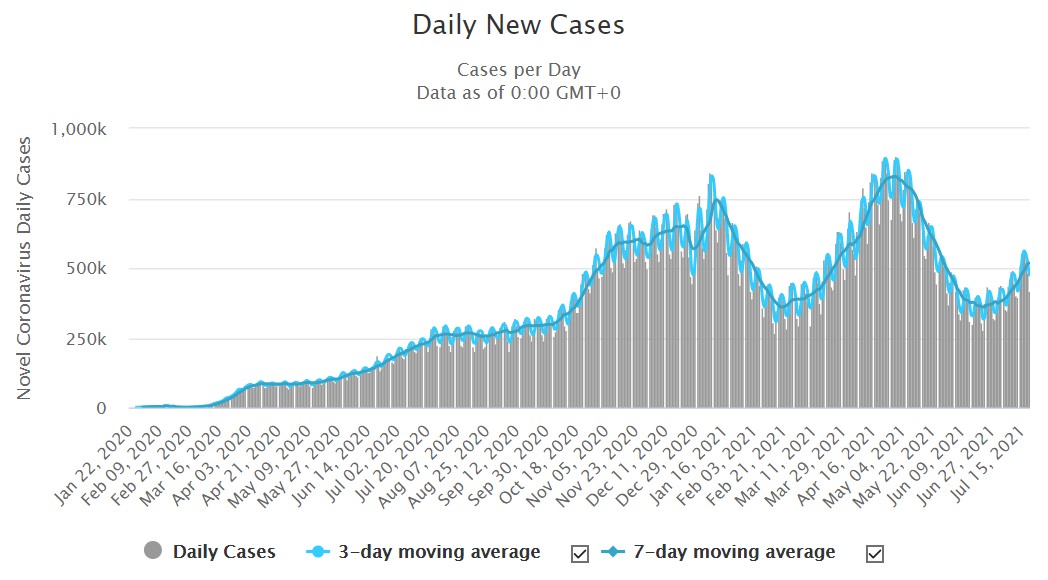
A Worldometer oldalán a világszerte regisztrált koronavírusos esetszámok grafikonján a háromnapos (világoskék) és a hétnapos (kék) mozgóátlag is megjeleníthető:
A 100. regisztrált esettől indított görbe
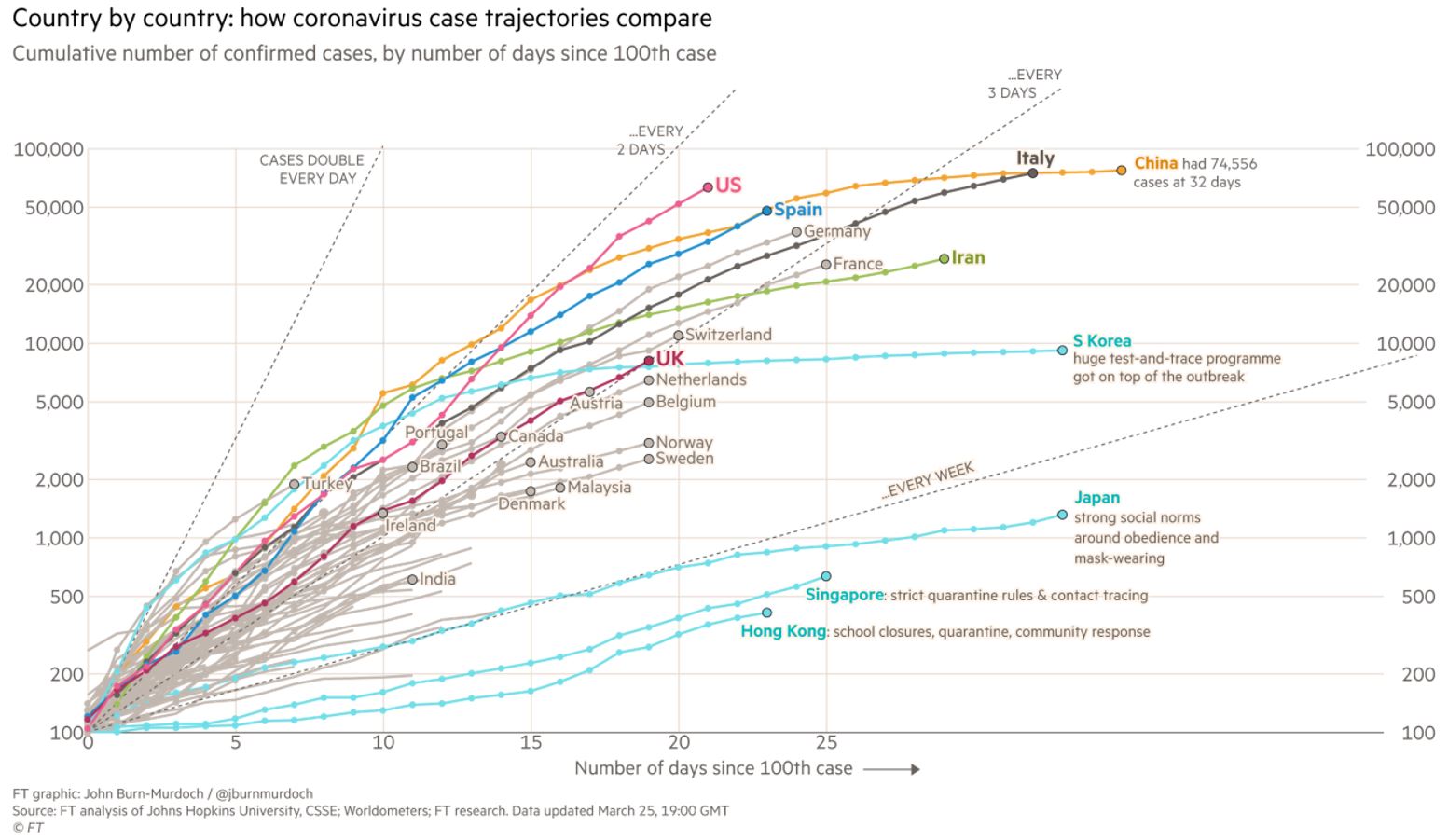
A koronavírus világszintű elterjedésével felmerült az igény, hogy az egyes országokat össze lehessen hasonlítani a járvány terjedésének gyorsasága és a védekezés sikeressége szempontjából. Nagy népszerűségre tett szert az a grafikon, amely az összes regisztrált esetszámot mutatja logaritmikus skálán, közös kezdőpontba helyezve az országokat. A közös kezdőpont a 100. regisztrált eset napja. A grafikon az ausztrál Grattan Institute oldalán jelent meg először, felkapottá akkor vált, amikor a Financial Times is elkészítette belőle a saját verzióját10. A grafikon elemzéséhez hasznos forrás angol nyelven a Financial Times feliratozott, magyarázatokkal ellátott verziója (lásd lejjebb), valamint a vox.com angol nyelvű magyarázó videója.
Egy olyan grafikon, amely nem az eltelt idő függvényében ábrázolja az adatokat
Tanulságos lehet az a grafikon, ami az összes eset függvényében ábrázolja az elmúlt hét (vagy nap) új eseteit. Az idő múlását az animáció érzékelteti. A Brilliant.org oktatási portál által készített angol nyelvű videó nyújt segítséget az értelmezéshez. Az Our World in Data oldalon is szerepel ez a diagramtípus a legfrissebb adatokkal. Itt mi magunk állíthatjuk össze, hogy mely országok grafikonjait szeretnénk megnézni, és megadhatjuk a tengelyek típusát is (lineáris/logaritmikus). A videóban látható animációból kiválasztottam egy képet, amelyet a videó megtekintése után kielemezhetünk.
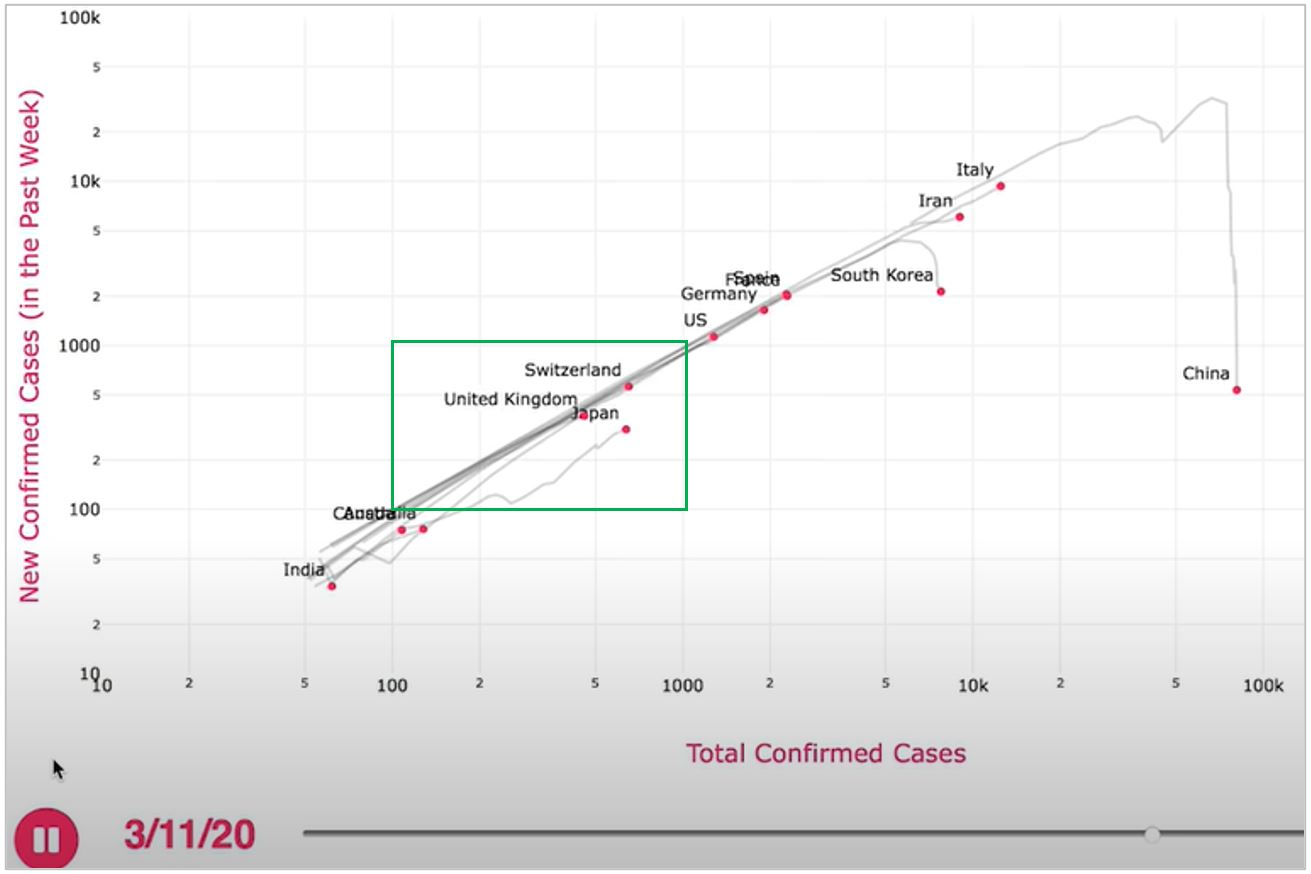
Néhány kérdés, amit feltehetünk a diákoknak:
1. A képen melyik nap adatai látszanak? (2020. március 11.)
2. Aznap körülbelül mennyi volt az összes regisztrált eset Kínában? (kb. 80 000. Egészen pontosan 80 778.11)
3. Nagyjából hány új esetet regisztráltak az ezt megelőző héten Kínában? (kb. 500-at.)
4. Amikor 50 000 volt Kínában az összes regisztrált eset száma, akkor körülbelül hány új beteget regisztráltak az előtte lévő héten? (kb. 20 000-et)
5. Nézzük a grafikonnak csak azt a részét, ami a zöld téglalapon belül található.
- Hányszorosára változott az összes esetszám? (10-szeresére)
- Hányszorosára változott az egy héten belül regisztrált esetek száma? (10-szeresére)
- Hány napot ölel fel a grafikonnak ez a része? (Ez nem megválaszolható. Egyrészt kell hozzá, hogy melyik országot nézzük, másrészt kell hozzá az animáció.)
6. Miből látszik, hogy a grafikonon látható időpontban Kína már jó úton haladt a vírus legyőzésében? (Az összes esetszám pici növekedésével a heti esetszám nagy csökkenése járt együtt.)
7. A grafikonon látható időpontban Kínán kívül melyik ország kezdett viszonylag jobban állni a vírus elleni harcban? (Dél-Korea.)
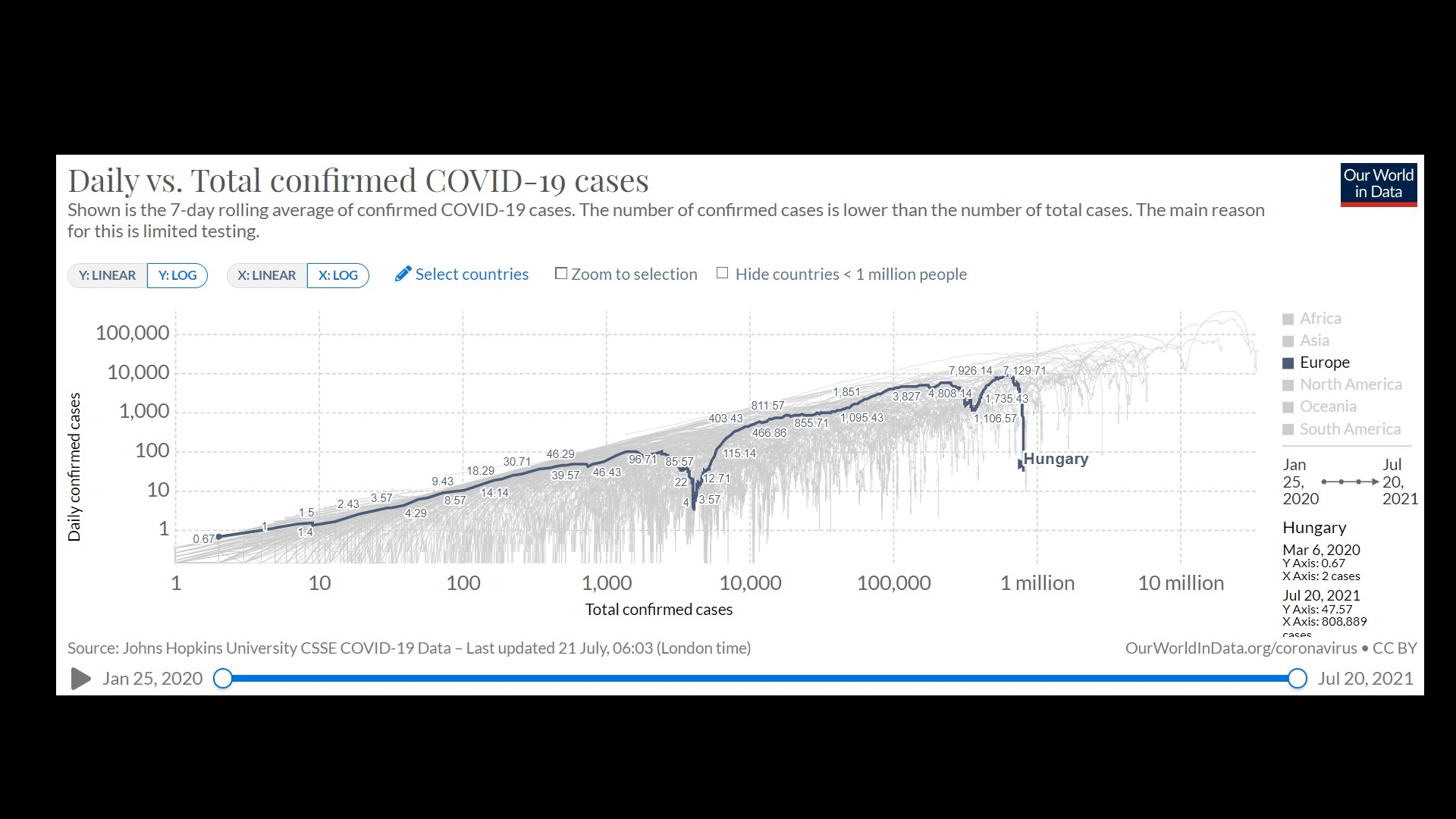
Az Our World in Data oldalon a magyarországi görbét kiválasztva ezt látjuk. (A videóban látotthoz képest itt a függőleges tengelyen a napi esetszám, nem pedig 7 nap összesített esetszáma szerepel.) Több ország kiválasztásával összehasonlító megállapításokat is tehetünk.
A SIR-modell
Az exponenciális növekedésről szóló részben láthattuk, hogy a járványterjedés első közelítésben exponenciális folyamatként írható le. Az új fertőzéseket mutató járványgörbén viszont azt láttuk, hogy az exponenciális növekedés a járvány lecsengésével lelassul. Ahhoz, hogy megjósolhassuk egy járvány lefutásának menetét, valóságközelibb modellek megalkotására van szükség. Ezek szinte mindegyike a rekeszes- vagy kompartment-modelleken alapul. Megértésük felsőbb matematikai ismereteket feltételez, középiskolásoknak nagy vonalakban lehet róluk szót ejteni. A modell matematika hátterének bemutatásához érdemes elolvasni Simon L. Péter Matematika a járványterjedés modellezésében című írását.
A legegyszerűbb kompartment-modell a vizsgált populáció tagjait három csoportba sorolja (megnevezése az angol kezdőbetűk alapján: SIR-modell):
 fogékonyak (Susceptible): azok az egyedek, akik fogékonyak a betegségre.
fogékonyak (Susceptible): azok az egyedek, akik fogékonyak a betegségre.
 fertőzők (Infective): a megfertőződött egyedek, akik képesek a fertőzés továbbadására.
fertőzők (Infective): a megfertőződött egyedek, akik képesek a fertőzés továbbadására.
 gyógyultak (Recovered vagy Removed): azok az egyedek, akik már nem kaphatják el a fertőzést vagy azért, mert már kigyógyultak és immunitást szereztek, vagy azért, mert elhunytak a betegség következtében.
gyógyultak (Recovered vagy Removed): azok az egyedek, akik már nem kaphatják el a fertőzést vagy azért, mert már kigyógyultak és immunitást szereztek, vagy azért, mert elhunytak a betegség következtében.
A SIR-modellt, az ebből generált grafikont és a görbe „lapításának” lehetőségeit mutatja be angolul a Numberphile videója. A modell deriváltakkal és differenciálegyenletekkel dolgozik, de az alapgondolat talán ezek ismerete nélkül is követhető valamelyest. A vállalkozó kedvűek reprodukálhatják GeoGebrában a videóban látható szimulációt.
Simon L. Péter cikkében láthatunk egy grafikont arról, hogy a 2016-os influenzajárványt vizsgálva milyen eltérést mutat a modell jóslata (kék csillagok) a valóságos adatokhoz képest (piros körök).
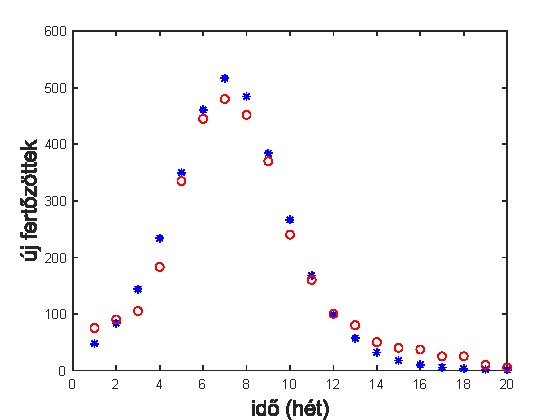
Még pontosabb előrejelzést tesz lehetővé, ha az S, I, R kategórián belül tovább bontjuk a populációt valamilyen szempont szerint. Garay Barna és Molnár Zsófia Nemlineáris dinamikai modellek a biológiában: a kontaktusmátrixos SIR-modell című cikkében életkor alapján határozott meg 3 kategóriát, és vizsgálta egy fiktív járvány lefutását korosztályonként korlátozások bevezetésével, illetve anélkül.
Valójában a járvány előrejelzésére szolgáló modell még ennél is jóval összetettebb. Röst Gergely 2020 áprilisi előadásában (1:17:49-től) a továbbfejlesztett változat komplexitását próbálja érzékeltetni.
Kun Ádámnak a Qubiten megjelent cikkében is szerepel néhány, a SIR-modell alapján készített szimuláció. A modell mögötti matematika megértése nélkül is hasznos lehet, ha elemezzük a diákokkal a grafikonokat.
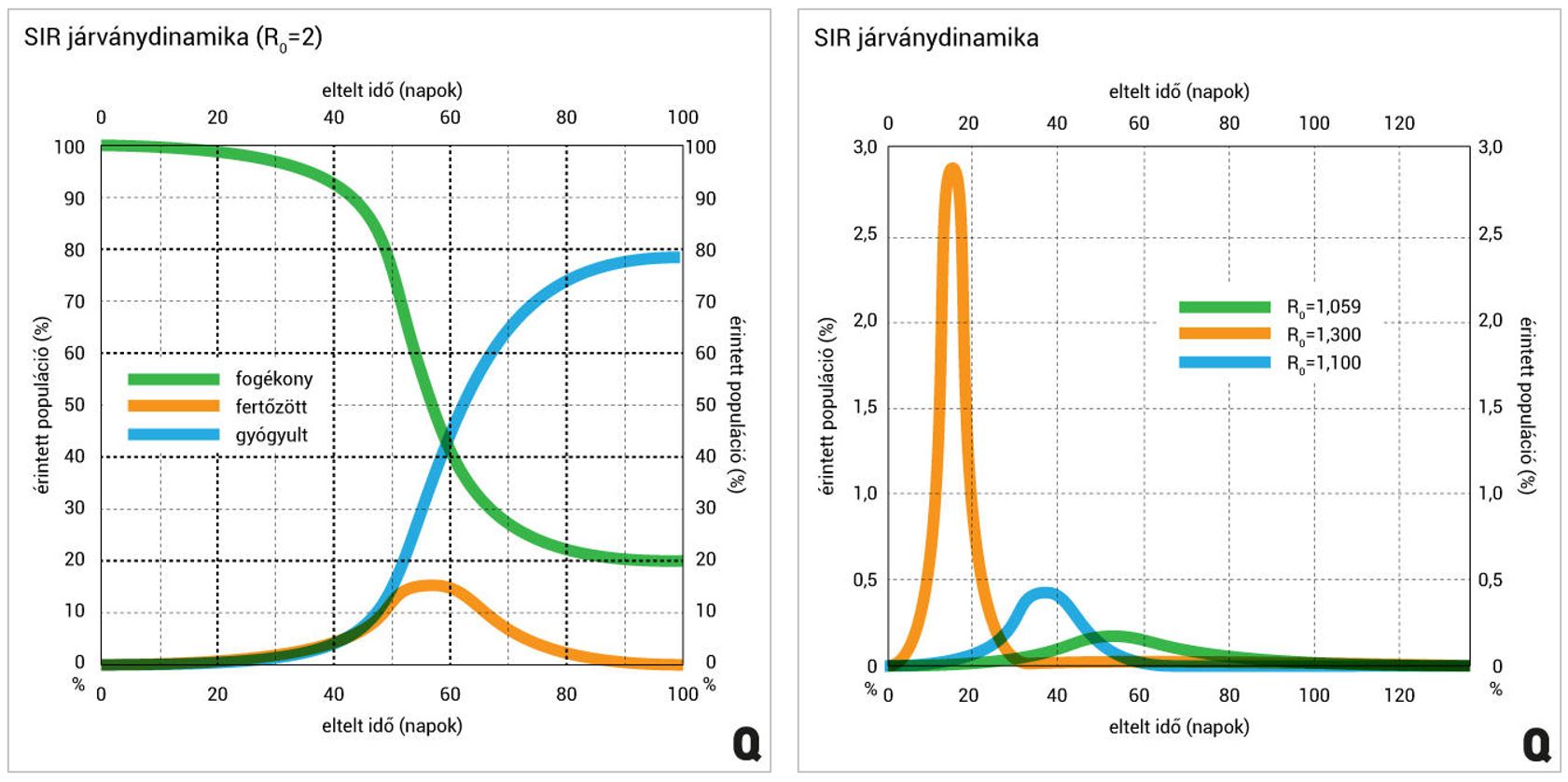
Volf Annamária
Városmajori Gimnázium
Lábjegyzetek
- 1 A tananyagban szereplő hivatkozások, görbék a 2021. júliusi állapotokat mutatják.
- 2 forrás: https://www.portfolio.hu/prof/20200310/hogyan-lehet-12-fertozottbol-12-ezer-a-koronavirus-matematikaja-418675
- 3 A nyájimmunitásról később lesz szó.
- 4 A kép forrása: https://hu.wikipedia.org/wiki/Szigmoid_függvények#/media/Fájl:Logistic-curve.svg
- 5 forrás: https://www.health.gov.au/news/health-alerts/novel-coronavirus-2019-ncov-health-alert/coronavirus-covid-19-case-numbers-and-statistics#daily-reported-cases
- 6 forrás: https://www.ncbi.nlm.nih.gov/books/NBK92467/
- 7 forrás: https://atlo.team/koronamonitor-reszletesadatok/#fertozottekbovebb
- 8 forrás: https://kurtakademia.hu/blog/kurt-akademia-live-7-7-kulcsgondolat-a-jarvanymodellezesrol/
- 9 forrás: https://24.hu/kulfold/2020/04/26/christian-drosten-koronavirus-interju-nemetorszag/
- 10 forrás: https://robjhyndman.com/hyndsight/logratios-covid19/
- 11 forrás: http://subsites.chinadaily.com.cn/nmpa/2020-03/12/c461928.htm









