1. Bevezető
„Csak azt kívánom, hogy az emberi faj jólétét ily közelről érintő ügyben ne hozzunk döntéseket a nélkül a tudás nélkül, aminek egy kevés elemzés és számítás útján birtokába kerülhetünk.” (Daniel Bernoulli1)
A koronavírus-járvány kapcsán olyan tudományterületek által használt fogalmak kerültek a köztudatba, mint a mikrobiológia, az epidemiológia vagy a járványmatematika. A járványterjedés modellezésével foglalkozó tudósok előrejelzéseket, szimulációkat készítenek. „A matematika segítségével tudjuk rendszerezni az adatainkat, azokat értelmezni, tudunk új összefüggéseket feltárni, kockázatokat számszerűsíteni. A dinamikus modelljeinkkel, differenciálegyenletek segítségével tudunk előrejelzéseket tenni (hányan fognak várhatóan megbetegedni, mikor éri el a járvány a csúcspontját...). Tudunk különböző intervenciós stratégiákat, vakcinálási stratégiákat kiértékelni, esetleg újabbakat javasolni.”2 Hazánkban a Járványmatematikai Modellező és Epidemiológiai Elemző Munkacsoport végzi ezt a munkát Röst Gergely vezetésével. Eredményeik a koronavírus-járvány kezdetén, 2020 januárjában kerültek először az érdeklődés középpontjába, amikor sikerült megbecsülniük az iráni járvány valós mértékét3.
Középiskolában a járványterjedés modellezésének összetett matematikai módszereire ugyan nem tudunk kitérni, de számos olyan, a matematikához kapcsolódó fogalomról, összefüggésről beszélhetünk, amely középiskolai tudással megérthető. Tapasztalatom szerint a diákoknak élményszerűvé teszi a matematika tanulását, és növeli a motivációjukat, ha a tananyagtól picit elrugaszkodva hallhatnak érdekességekről, a mindennapokban előforduló jelenségekről. A járvány kapcsán egy újabb példát láthatnak arra, hogy az életünket milyen módon befolyásolhatja ez a tudományág.
Ez az összeállítás4 talán lerövidíti a felkészülést, ha egy-egy tanórán a Covid-járvány matematikai vonatkozásairól szeretnénk beszélni a diákokkal. A csoport matektudásának, a rendelkezésünkre álló időnek vagy éppen az aktuális tananyagnak megfelelően válogathatunk belőle, de segítségével akár közös projekteket is szervezhetünk a biológia, informatika vagy angol szakos kollégákkal. (Utóbbi tantárgyhoz az angol nyelvű források miatt, előbbihez a táblázatkezelőben megoldható számolási feladatok miatt tudunk kapcsolódni.) Bizonyos részeket önálló feldolgozásra is kiadhatunk, de akár kiselőadásra is felkészülhetnek belőle a diákok.
A cikksorozat első részében szó lesz arról, hogy mit jelent az exponenciális növekedés, és hogy hol találkozunk vele a járványterjedés kapcsán. Kitérünk olyan fogalmakra is, mint a reprodukciós szám és a nyájimmunitás. A második részben néhány érdekesebb járványgörbét tekintünk át, továbbá szót ejtünk a járványok terjedését leíró SIR-modellről. A harmadik rész az egészségügyi tesztek megbízhatóságával, valamint a vakcinák hatékonyságával kapcsolatos számításokkal foglalkozik.
Mi az exponenciális növekedés?
Példák exponenciális változásra
Annak ellenére, hogy a mindennapokban is találkozunk exponenciálisan változó mennyiségekkel, az emberek nagy százaléka alulbecsüli az exponenciális növekedés mértékét.5 A lineáris változásokat egyszerűbben meg tudjuk becsülni, míg az exponenciális változások esetén nehéz elképzelnünk, hogy egy kicsi érték rövid idő alatt a sokszorosára növekedhet.
Az exponenciális változás gyorsaságának érzékeltetésére négy példát választottam, amelyek végeredményét a végigszámolás előtt érdemes megtippeltetni a diákokkal. Az első két feladat egy-egy mértani sorozat 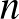 -edik tagját kérdezi, míg a második kettő az első
-edik tagját kérdezi, míg a második kettő az első 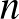 tag összegére is rákérdez. A diákok matektudásának megfelelően akár általánosíthatjuk is a feladatokat.
tag összegére is rákérdez. A diákok matektudásának megfelelően akár általánosíthatjuk is a feladatokat.
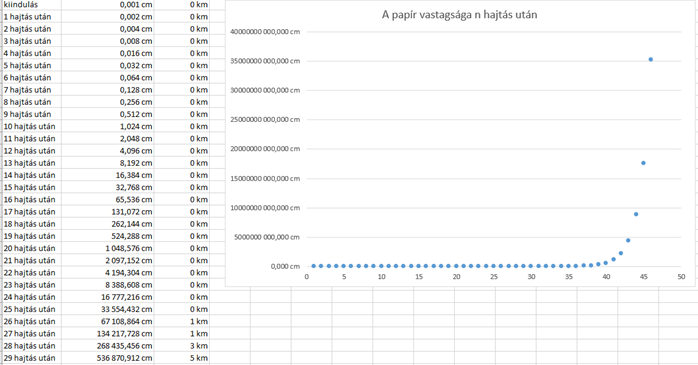
1. Képzeljük el, hogy adott egy végtelenül nagy, de mindössze 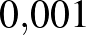 cm vastag papírlap, amit akárhányszor félbe tudunk hajtani. Nagyjából milyen magas lesz 45 hajtás után?
cm vastag papírlap, amit akárhányszor félbe tudunk hajtani. Nagyjából milyen magas lesz 45 hajtás után?
Ehhez a klasszikus problémához számos szemléltető-magyarázó videót találunk elsősorban angol nyelven.
 Szemléltetés: Angol nyelvű TED-Ed videó magyar felirattal (Exponenciális növekedés: Hogyan juthatsz el papírhajtogatással a Holdig?)
Szemléltetés: Angol nyelvű TED-Ed videó magyar felirattal (Exponenciális növekedés: Hogyan juthatsz el papírhajtogatással a Holdig?)
 Gyakorlati bemutató: A MythBusters csapata 11-szer hajt félbe egy focipályányi papírlapot (angol nyelvű videó felirat nélkül)
Gyakorlati bemutató: A MythBusters csapata 11-szer hajt félbe egy focipályányi papírlapot (angol nyelvű videó felirat nélkül)
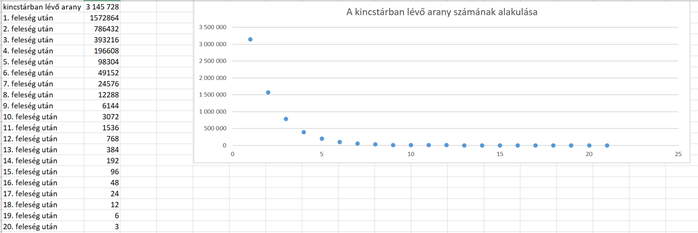
2. A szultán kincstárában 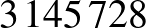 aranypengő van. Elhatározza, hogy szétosztja a feleségei között. Első nap magához hívatja a kedvenc feleségét, és odaadja neki a kincstárban lévő arany felét. A második nap a második feleségének adja oda a megmaradt arany felét, és ezt így folytatja egészen addig, amíg csak 3 aranya marad. Hány feleséget tudott megjutalmazni a szultán?
aranypengő van. Elhatározza, hogy szétosztja a feleségei között. Első nap magához hívatja a kedvenc feleségét, és odaadja neki a kincstárban lévő arany felét. A második nap a második feleségének adja oda a megmaradt arany felét, és ezt így folytatja egészen addig, amíg csak 3 aranya marad. Hány feleséget tudott megjutalmazni a szultán?
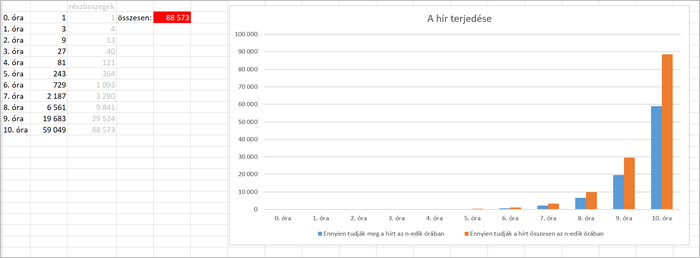
3. Megnyerted a lottó 5-öst, és erről bizalmasan értesíted a 3 legjobb barátodat. Megkéred őket, hogy senkinek ne adják tovább a nagy hírt. Biztosítanak róla, hogy megbízhatsz bennük, de természetesen nem bírják megtartani a titkot, és egy órán belül mindegyikük elmondja 3-3 embernek. Ha mindenki, aki megtudta a hírt, 1 órán belül 3 embernek tovább is adja, hányan fogják tudni 10 óra múlva, hogy Te nyertél? (Tegyük fel, hogy mindenki csak olyan embernek adja tovább a hírt, aki még nem tud róla.)
4. A monda szerint a sakkjáték felfedezője is felvetett egy matematikai problémát az őt megjutalmazni kívánó uralkodónak. Ugyanis jutalmát rizsszemekben kérte, mégpedig úgy, hogy tegyen az uralkodó a sakktábla első mezőjére egy rizsszemet, a következőre kettőt, az azután következőre négyet és így tovább, mindig kétszer annyi szemet, mint amennyi az előzőn volt. Folytassa ezt addig, amíg a 64. mezőig el nem ér. Körülbelül hány rizsszem a jutalom összesen?
Angol nyelvű szemléltető videó: Rizsszemek a sakktáblán – egy exponenciális történet
Végezzük el a számolást egy táblázatkezelő programban, a kapott értékeket pedig ábrázoljuk pontdiagramon! (Az Excel csak 15 értékes jegy tárolására képes, így lesz olyan feladat, amelynek a végeredményét csak kerekítve tudja megjeleníteni.)
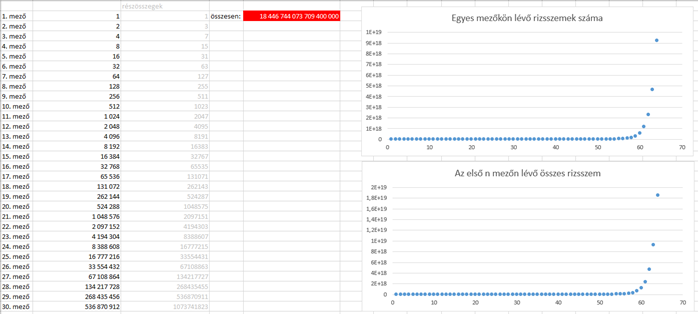
Az első 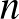 mezőn lévő rizsszemek számának meghatározása:
mezőn lévő rizsszemek számának meghatározása:
A keresett összeg legyen 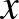 .
.
Tudjuk, hogy 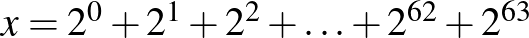 .
.
Szorozzuk meg 2-vel ezt az egyenlőséget: 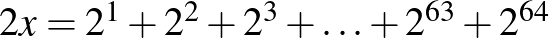 .
.
Vonjuk ki egymásból a két egyenletet és ejtsük ki az azonos tagokat: 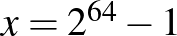 .
.
A rizsszemek számának pontos értéke: 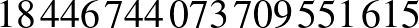 darab.
darab.
A példák után megfogalmazhatjuk az általános észrevételt: egy mennyiség időbeli változása exponenciális, ha bárhogyan is választunk két egyenlő időtartamot, a mennyiség mindkét időtartam alatt ugyanannyiszorosára változik.
Az exponenciális függvény precíz definiálása előtt megfogalmazhatunk néhány, a megértést segítő kérdést:
 Határozzuk meg az exponenciális változást leíró szorzót az egyes feladatokban!
Határozzuk meg az exponenciális változást leíró szorzót az egyes feladatokban!
 Miből látszik, hogy az exponenciális változás növekedés vagy csökkenés lesz-e?
Miből látszik, hogy az exponenciális változás növekedés vagy csökkenés lesz-e?
 Összeköthetjük-e a grafikonjaink pontjait?
Összeköthetjük-e a grafikonjaink pontjait?
Az exponenciális függvény precíz matematikai bevezetéséhez használhatjuk a ZanzaTv videóját.
További példák exponenciálisan változó mennyiségekre:
 A ZanzaTv újabb videója két, a hétköznapi életben előforduló exponenciális folyamatot elemez (a Föld népességének növekedése, egy autó értékének változása), továbbá elmagyarázza az exponenciális csökkenés kapcsán a felezési idő fogalmát.
A ZanzaTv újabb videója két, a hétköznapi életben előforduló exponenciális folyamatot elemez (a Föld népességének növekedése, egy autó értékének változása), továbbá elmagyarázza az exponenciális csökkenés kapcsán a felezési idő fogalmát.
 Klasszikus példa az exponenciális növekedésre a piramisjátékok működése. Ennek a rövid bemutatására alkalmas például a TED-Ed „How to spot a pyramid scheme” című, angol nyelvű animációs videója.
Klasszikus példa az exponenciális növekedésre a piramisjátékok működése. Ennek a rövid bemutatására alkalmas például a TED-Ed „How to spot a pyramid scheme” című, angol nyelvű animációs videója.
A középiskolai tananyagban az exponenciális folyamatok között kiemelt szerepet kap a kamatos kamat. Érdemes egy példa erejéig kitérni erre a feladattípusra is.
Kamatos kamatszámításnál minden tőkésítési periódus (pl év) végén a kamatot a tőkéhez csatolják, a következő periódusban a kamattal növelt tőke kamatozik.
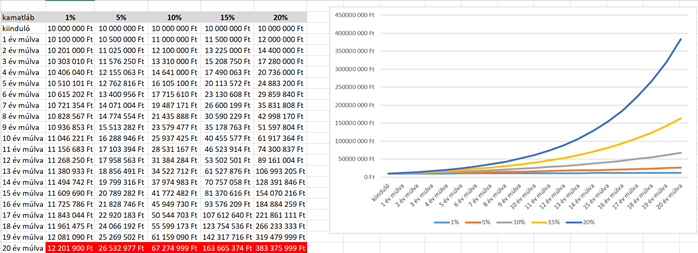
Tegyük fel, hogy fel szeretnénk venni 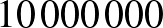 Ft lakáshitelt 20 évre. Nézzük meg, hogy a 20 év alatt mennyi pénzt fizetünk vissza, ha a lakáshitel kamata 1%, 5%, 10%, 15% vagy 20%. Az egyes kamatlábakhoz tartozó grafikonokat érdemes egy koordináta-rendszerben ábrázolni. (Nézzünk utána, hogy a fenti kamatlábak közül melyek állnak legközelebb a valós adatokhoz!)
Ft lakáshitelt 20 évre. Nézzük meg, hogy a 20 év alatt mennyi pénzt fizetünk vissza, ha a lakáshitel kamata 1%, 5%, 10%, 15% vagy 20%. Az egyes kamatlábakhoz tartozó grafikonokat érdemes egy koordináta-rendszerben ábrázolni. (Nézzünk utána, hogy a fenti kamatlábak közül melyek állnak legközelebb a valós adatokhoz!)
| kamatláb | szorzó | képlet | végeredmény |
| 1% | 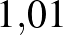 |
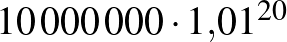 |
12 201 900 |
| 5% | 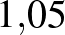 |
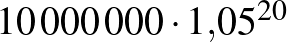 |
26 532 977 |
| 10% | 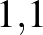 |
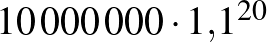 |
67 274 999 |
| 15% | 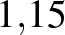 |
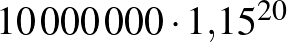 |
163 665 374 |
| 20% | 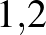 |
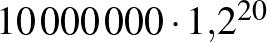 |
383 375 999 |
Szemléltetés táblázatkezelőben:
A logaritmikus skála
Az exponenciális folyamatokat leíró függvények nagyon gyorsan változnak, és nagyságrendekkel eltérő adatokat tartalmaznak. A logaritmikus skála előnye, hogy nagyon nagy és nagyon kicsi adatokat egyaránt ábrázolhatunk a segítségével.
Nézzük példaként az 1. feladatot a rizsszemekkel. (Emlékeztető: az exponenciális növekedés szorzója ebben a feladatban 2 volt.)
Készítsük el a grafikonját 2-es alapú logaritmikus skálán! (Excelben is használhatunk logaritmikus skálát: Jobb kattintás az értéktengelyre/Tengely formázása/Tengely beállításai/Logaritmikus skála, alapja: 2.) A 2-es alapú logaritmikus skála értéktengelyén az egységek a kettőhatványok lesznek.
Megoldás:
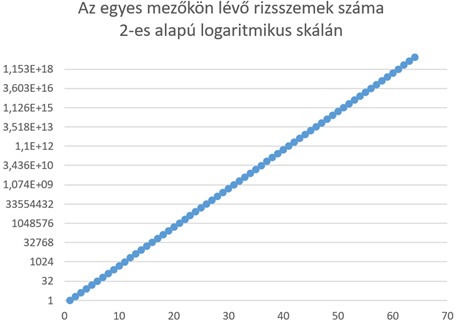
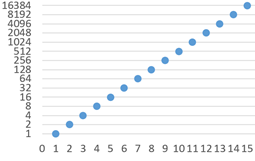
Kiemelve a bal alsó sarok a könnyebb értelmezhetőség kedvéért:
A Koronamonitor oldalon megtaláljuk a magyarországi összes regisztrált fertőzött számát mutató diagramot, amelyek nézetét lineárisra és logaritmikusra is állíthatjuk.
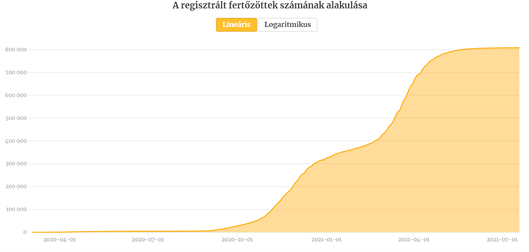
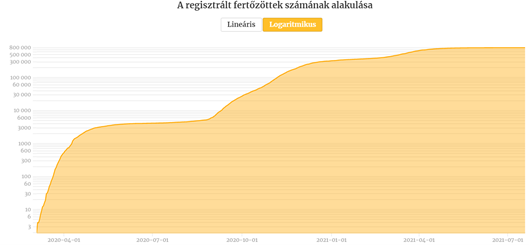
Nemzetközi adatokról hasonló digramokat találunk a worldometers.info oldalon.
A tőzsdei elemzések során is hasznos lehet a logaritmikus skála alkalmazása, az elemzeskozpont.hu írása több példa segítségével szemlélteti az előnyeit.
A földrengések erősségét6 mérő Richter-skála is 10-es alapú logaritmikus, azaz eggyel nagyobb számmal jelzett földrengés a valóságban 10-szer nagyobb erősségű.7
2. Exponenciális növekedés a járványterjedésben
A reprodukciós szám
A járványmodellezés egyik legfontosabb paramétere a koronavírussal kapcsolatban is emlegetett reprodukciós szám. Az effektív reprodukciós szám (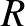 ) azt fejezi ki, hogy egy fertőzött beteg átlagosan hány embernek adja át a vírust. Ha ez az érték 1-nél nagyobb, akkor a vírus könnyen terjedhet, míg ha annál kisebb, akkor várhatóan le fog csengeni. Az alap vagy elemi reprodukciós szám (
) azt fejezi ki, hogy egy fertőzött beteg átlagosan hány embernek adja át a vírust. Ha ez az érték 1-nél nagyobb, akkor a vírus könnyen terjedhet, míg ha annál kisebb, akkor várhatóan le fog csengeni. Az alap vagy elemi reprodukciós szám (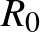 ) a vírus fertőzőképességét mutatja a korlátozó intézkedések, védőoltás nélkül. Figyelembe vesz viszont olyan tényezőket, mint a zsúfoltság, a higiénia, a vírus terjedésének módja, vagy hogy milyen hosszú ideig fertőz az, aki elkapta. Gyakorlatilag azt mutatja meg, hogy a járvány kezdetén, amikor még senki sem immunis a fertőzésre, milyen gyorsan tud terjedni a vírus.8
) a vírus fertőzőképességét mutatja a korlátozó intézkedések, védőoltás nélkül. Figyelembe vesz viszont olyan tényezőket, mint a zsúfoltság, a higiénia, a vírus terjedésének módja, vagy hogy milyen hosszú ideig fertőz az, aki elkapta. Gyakorlatilag azt mutatja meg, hogy a járvány kezdetén, amikor még senki sem immunis a fertőzésre, milyen gyorsan tud terjedni a vírus.8
Összefoglaló ábra:9
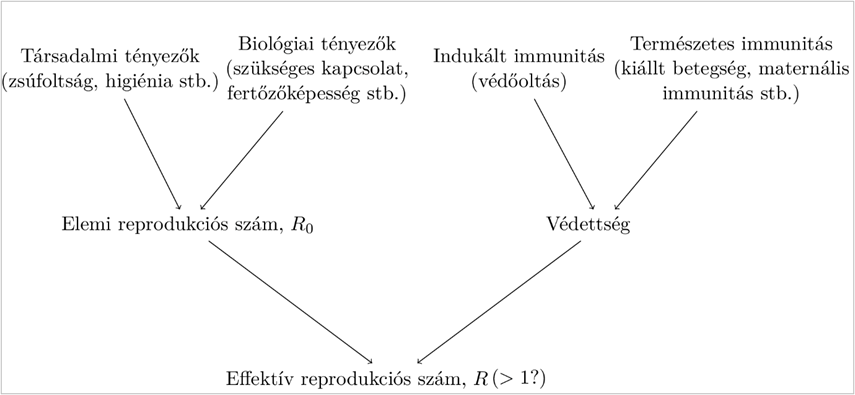
A reprodukciós számra általában intervallumot adnak meg, mert a társadalmi tényezők akár még egy-egy országon belül is eltérőek lehetnek.
A magyarországi koronavírus-járvány effektív reprodukciós számának (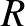 ) becslése a Koronamonitoron:
) becslése a Koronamonitoron:
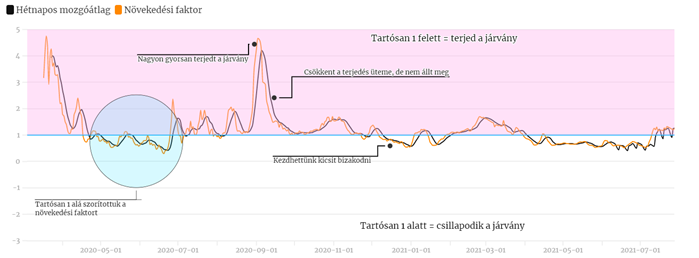
Hol van az exponenciális növekedés?
A járványterjedés pontos modellezésének a matematikája nagyon bonyolult, de első közelítésben nézzünk egy leegyszerűsített számítást annak az ellenőrzésére, hogy valóban exponenciális növekedésről van szó.
Tegyük fel, hogy egy városban 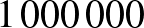 lakos él, és közülük egyvalaki fertőzött. Legyen
lakos él, és közülük egyvalaki fertőzött. Legyen 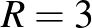 . Feltételezzük továbbá, hogy minden fertőzött pontosan ennyi embernek adja át a vírust rögtön a fertőzését követő napon, és hogy az ezt követő napokon már nem fertőz. Adjunk képletet arra, hogy a
. Feltételezzük továbbá, hogy minden fertőzött pontosan ennyi embernek adja át a vírust rögtön a fertőzését követő napon, és hogy az ezt követő napokon már nem fertőz. Adjunk képletet arra, hogy a 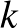 -adik napon hány ember fertőződik meg a koronavírussal! Módosítsuk a modellt, nézzük meg, mi történik, ha
-adik napon hány ember fertőződik meg a koronavírussal! Módosítsuk a modellt, nézzük meg, mi történik, ha 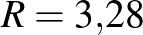 ,
, 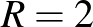 ,
, 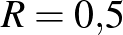 ! Az általános képlet felírásával igazoljuk, hogy exponenciális kifejezést kapunk! (Megoldás:
! Az általános képlet felírásával igazoljuk, hogy exponenciális kifejezést kapunk! (Megoldás: 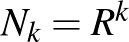 .)
.)
Azt is kiszámolhatjuk, hogy hány olyan ember lesz 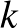 nap múlva, aki már elkapta a vírust. (Tehát vagy éppen fertőzött, vagy már átesett a fertőzésen.)
nap múlva, aki már elkapta a vírust. (Tehát vagy éppen fertőzött, vagy már átesett a fertőzésen.)
Megoldás:
A keresett összeg legyen 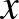 .
. 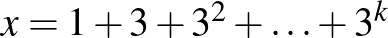 .
.
Szorozzuk az egyenletet 3-mal: 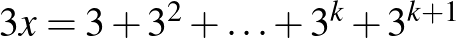 .
.
Vonjuk ki egymásból az egyenleteket: 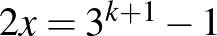 .
.
Osszunk 2-vel: 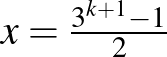 .
.
Az adatok ábrázolása táblázatkezelőben:
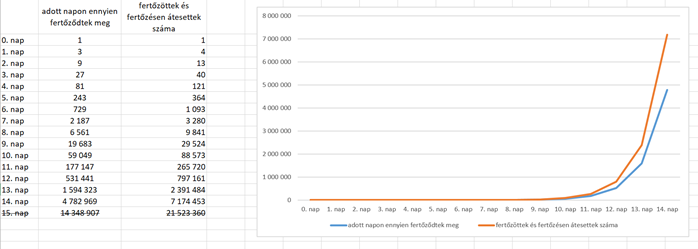
Röst Gergely előadásának inkjére kattintva a koronavírus matematikájáról szóló előadás egy részletét nézhetjük meg10. A videó 2020. április végén készült, ekkor a reprodukciós számra adott becslés 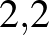 volt. A kivetített dián az látható, hogy a különböző mértékű korlátozások esetén mennyire csökken le az effektív reprodukciós szám.
volt. A kivetített dián az látható, hogy a különböző mértékű korlátozások esetén mennyire csökken le az effektív reprodukciós szám.
Az alábbi táblázat néhány vírus alap reprodukciós számát tartalmazza11:
| Betegség | Terjedés | 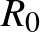 |
| Kanyaró | Levegőben | 12–18 |
| Bárányhimlő | Levegőben | 10–12 |
| Szamárköhögés | Cseppfertőzéssel | 12–17 |
| Diftéria | Nyállal | 6–7 |
| Himlő | Társas érintkezéssel | 5–7 |
| Járványos gyermekbénulás (polio) | Széklettel | 5–7 |
| Rózsahimlő (rubeola) | Cseppfertőzéssel | 5–7 |
| Mumpsz | Cseppfertőzéssel | 4–7 |
| COVID–19 | Cseppfertőzéssel | 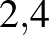 –812 –812 |
| HIV/AIDS | Nemi úton | 2–5 |
| SARS | Cseppfertőzéssel | 2–5 |
| Spanyolnátha (az 1918-as világjárványt okozó influenza) | Cseppfertőzéssel | 2–3 |
| Ebola (a 2014-es járványt okozó törzs) | Testnedvekkel | 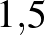 – –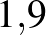 |
| Influenza (a 2009-es járványt okozó törzs) | Cseppfertőzéssel | 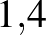 – –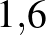 |
| MERS | Cseppfertőzéssel | 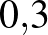 – –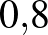 |
A magas alap reprodukciós szám (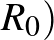 nem mindig jár együtt rengeteg beteggel (azaz magas effektív szaporodási rátával), mert ez utóbbit más faktorok és különféle beavatkozások is módosítják (pl. védőoltás, korlátozó intézkedések). A SARS koronavírus esetében például 2 és 3 közé tették az
nem mindig jár együtt rengeteg beteggel (azaz magas effektív szaporodási rátával), mert ez utóbbit más faktorok és különféle beavatkozások is módosítják (pl. védőoltás, korlátozó intézkedések). A SARS koronavírus esetében például 2 és 3 közé tették az 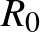 értékét, mégis csak 8000 embert fertőzött meg. Ehhez képest az influenza alap szaporodási rátája a becslések szerint
értékét, mégis csak 8000 embert fertőzött meg. Ehhez képest az influenza alap szaporodási rátája a becslések szerint 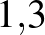 körül lehet, mégis milliókat fertőz meg évente.
körül lehet, mégis milliókat fertőz meg évente.
Összefüggés 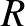 és
és 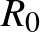 között13
között13
Legyen 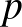 a védettek14 aránya a populáción belül (
a védettek14 aránya a populáción belül ( ![$p\in [0;1]$](/images/stories/latexuj/2021-08/2021-08-volfannamariajarvanymatematika1/img47.png) ). Más megfogalmazásban:
). Más megfogalmazásban: 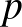 annak a valószínűsége, hogy a populációból véletlenszerűen választva egy egyedet, ő védett a fertőzéssel szemben. Ekkor a nem védettek aránya a populáción belül
annak a valószínűsége, hogy a populációból véletlenszerűen választva egy egyedet, ő védett a fertőzéssel szemben. Ekkor a nem védettek aránya a populáción belül 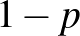 . (Például ha a populáció
. (Például ha a populáció 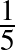 része védett, akkor
része védett, akkor 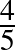 része nem az.)
része nem az.)
Kezdetben legyen 1 fertőzött egyedünk.
Ő 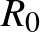 másik embert fertőzne meg, ha nem lennének védett egyedek.
másik embert fertőzne meg, ha nem lennének védett egyedek.
De valójában az 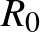 egyedből csak azokat sikerül megfertőznie, akik nem védettek. Mivel a nem védettek aránya
egyedből csak azokat sikerül megfertőznie, akik nem védettek. Mivel a nem védettek aránya 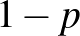 , ezért valójában összesen
, ezért valójában összesen 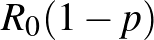 egyed fertőződik meg. A képlet eredménye az effektív reprodukciós szám (
egyed fertőződik meg. A képlet eredménye az effektív reprodukciós szám (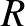 ). (Ha
). (Ha 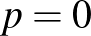 , azaz ez egy új járvány és még nincsenek védett egyedek, akkor a definíciónak megfelelően
, azaz ez egy új járvány és még nincsenek védett egyedek, akkor a definíciónak megfelelően 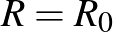 .)
.)
A járvány kitörésének feltétele tehát, hogy 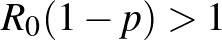 legyen.
legyen.
3. A nyájimmunitással kapcsolatos számítások
A koronavírus kapcsán sokat lehetett hallani a nyájimmunitás vagy közösségi immunitás fogalmáról. Nyájimmunitásról fertőző betegségek esetén beszélünk. „Úgy jön létre, hogy a népesség egy bizonyos részének beoltása vagy kigyógyulása védettséget biztosít a beoltatlanok számára is. Azaz, bár nem mindenki immunis a populációban, de az egész közösség együtt az. Egy népességben azok az egyének, akik immunitást szereztek, nem járulnak hozzá a kórokozó továbbterjedéséhez. Ilyen közösségben a fertőzésláncok nagyobb valószínűséggel szakadnak meg, a terjedés ezért lelassul, vagy meg is áll. A közösség minél több tagja szerez immunitást, annál kisebb a valószínűsége, hogy a többiek találkoznak a kórokozóval.”15 A Szertár 2020-as videója szemléletesen magyarázza el a nyájimmunitás fogalmát.
Hogy a népesség mekkora részének kell átfertőződnie, illetve védőoltást kapnia a nyájimmunitás kialakulásához, az az adott kórokozó fertőzőképességétől függ. A nyájimmunitással kapcsolatos számolásokhoz Ferenci Tamás cikkét vesszük alapul.
Az 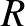 és
és 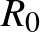 közötti összefüggés vizsgálatakor a járvány kitörésének feltételére az
közötti összefüggés vizsgálatakor a járvány kitörésének feltételére az 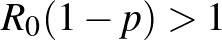 összefüggést kaptuk, ahol
összefüggést kaptuk, ahol 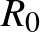 az alap reprodukciós szám,
az alap reprodukciós szám, 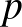 pedig a védettek aránya a populáción belül. A fenti egyenlőtlenségből
pedig a védettek aránya a populáción belül. A fenti egyenlőtlenségből 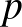 -t kifejezve a következőt kapjuk:
-t kifejezve a következőt kapjuk: 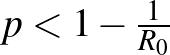 . Azaz a járvány kitörésének feltétele, hogy a védettek aránya, azaz
. Azaz a járvány kitörésének feltétele, hogy a védettek aránya, azaz 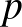
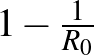 -nál kisebb legyen. A járvány lecsengésének feltétele is felírható ebből:
-nál kisebb legyen. A járvány lecsengésének feltétele is felírható ebből: 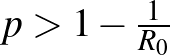 . Ha egy járvány ellen csak a védőoltás biztosít immunitást, akkor ez az arány megadja, hogy a populáció hanyadrészének kell beoltva lennie, hogy ne törjön ki a járvány.
. Ha egy járvány ellen csak a védőoltás biztosít immunitást, akkor ez az arány megadja, hogy a populáció hanyadrészének kell beoltva lennie, hogy ne törjön ki a járvány.
Ez alapján az alábbi táblázatot ki tudjuk egészíteni azzal az értékkel, hogy hány százalékos védettség ad nyájimmunitást. Helyettesítsük be a fenti képletbe az 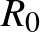 értékeket!
értékeket!
| Betegség | 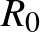 |
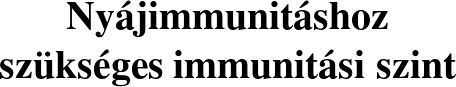 |
| Kanyaró | 12–18 | |
| Bárányhimlő | 10–12 | |
| Szamárköhögés | 12–17 | |
| Diftéria | 6–7 | |
| Himlő | 5–7 | |
| Járványos gyermekbénulás (polio) | 5–7 | |
| Rózsahimlő (rubeola) | 5–7 | |
| Mumpsz | 4–7 | |
| COVID–19 | 2,4–8 | |
| HIV/AIDS | 2–5 | |
| SARS | 2–5 | |
| Spanyolnátha (1918) | 2–3 | |
| Ebola (a 2014-es járványt okozó törzs) | 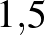 – –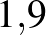 |
|
| Influenza (a 2009-es járványt okozó törzs)16 | 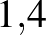 – –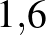 |
Megoldás:
| Betegség | 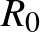 |
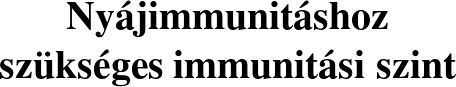 |
| Kanyaró | 12–18 | 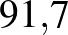 %– %–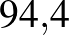 % % |
| Bárányhimlő | 10–12 | 90%–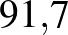 % % |
| Szamárköhögés | 12–17 | 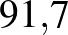 %– %–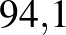 % % |
| Diftéria | 6–7 | 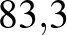 %– %–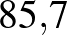 % % |
| Himlő17 | 5-7 | 80% - 85,7% |
| Járványos gyermekbénulás (polio) | 5–7 | 80% - 85,7% |
| Rózsahimlő (rubeola) | 5–7 | 80% - 85,7% |
| Mumpsz | 4–7 | 75%–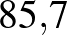 % % |
| COVID–19 | 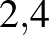 –8 –8 |
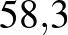 %– %–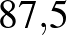 %18 %18 |
| HIV/AIDS | 2–5 | 50%–80% |
| SARS | 2–5 | 50%–80% |
| Spanyolnátha (1918) | 2–3 | 50%–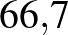 % % |
| Ebola (a 2014-es járványt okozó törzs) | 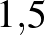 – –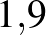 |
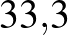 %– %–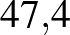 % % |
| Influenza (a 2009-es járványt okozó törzs) | 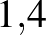 – –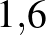 |
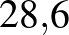 %– %–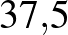 % % |
Néhány szó a kanyaróról a nyájimmunitás szemszögéből
Nézzük meg a Mindenki Akadémiája sorozatból Röst Gergely előadását, amelynek címe A védőoltások matematikája!
A videóban szereplő egyik példa a kanyaró, amely a magas oltottságnak köszönhetően visszaszorult, majd több helyen újra megjelent19, ahogy az átoltott népesség elkezdett kihalni, az újszülötteket pedig kisebb arányban oltották be, mint ami a nyájimmunitáshoz szükséges lett volna (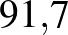 %–
%– %).
%).
Egy jó oltási program eredményét mutatja az első grafikon. A fekete vonal az oltás bevezetésének időpontját jelzi:
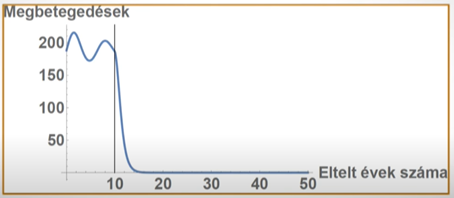
Ha 90% helyett 70%-os a beoltottság, akkor a járvány hullámokban visszatér:
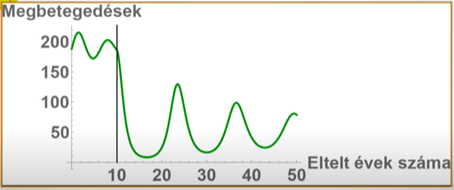
A majdnem tökéletes, 85%-os oltottság esetén is hasonló visszatérő hullámot kapunk, csak hosszabb lesz a szünet az egymást követő járványhullámok között.
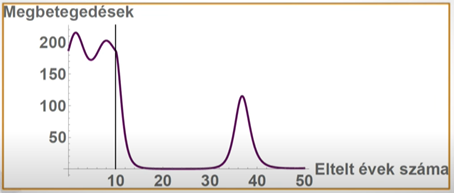
A kanyaróval kapcsolatban érdemes kiemelni a 2012-es foci EB-ről szóló részt. A versenysorozat egyik házigazdája Ukrajna volt, ahol az EB időpontjában kanyarójárvány zajlott.20 Mivel több európai országban a kanyaró elleni oltottság szintje 90% alatt van, ezért megvolt rá az esély, hogy az Ukrajnába utazó szurkolók elkapják a betegséget, és a saját országukba visszahurcolva járványt robbantanak ki. A legnagyobb kockázatot a franciák jelentették, mert ott volt a legalacsonyabb az átoltottság. Járványügyi szempontból szerencse, hogy a francia csapat hamar kiesett, a szurkolók hazamentek, és nem okoztak járványt Franciaországban.
A cikk második részében szó lesz járványgörbékről, illetve a járványok terjedését leíró SIR-modellről.
Volf Annamária
Városmajori Gimnázium
Lábjegyzetek
- 1 Daniel Bernoulli 18. századi orvos, matematikus és fizikus. Többek között a feketehimlő ellen alkalmazott védekezési eljárással, a variolációval kapcsolatban végzett fontos számításokat.
- 2 Részletek Röst Gergely előadásából (A védőoltások matematikája – Mindenki Akadémiája) https://www.youtube.com/watch?v=vCbuu747t-w.
- 3 https://index.hu/techtud/2020/03/05/magyar_matematikusok_a_koronavirus-jarvany_fo_modellezoi_kozott/
- 4 A tananyagban szereplő hivatkozások, görbék a 2021. júliusi állapotokat mutatják.
- 5 Forrás: https://qubit.hu/2020/07/21/aki-megerti-az-exponencialis-novekedest-nagyobb-esellyel-fogadja-el-a-jarvanyugyi-intezkedeseket.
- 6 A rengés erőssége a földrengés helyétől 100 km távolságban lévő szeizmográf által mikrométerben mért legnagyobb kitérés tízes alapú logaritmusa. Forrás: https://hu.wikipedia.org/wiki/Richter-skála
- 7 A Richter-skála szerinti erősség mellett egy földrengés fontos jellemzője a magnitúdó, ami a földrengés során felszabaduló energiával függ össze. Ezt szintén logaritmikus skálán definiáljuk: egy magnitúdófokozat növekedés mintegy 32-szeres energia növekedést jelent. Forrás: http://www.foldrenges.hu/index.php?option=com_content&view=article&id=15:magnitudo&catid=19&Itemid=23.
- 8 Magyarázat a Zállatorvos videójából 16:13-tól: https://youtu.be/j0RijCfdlGE?t=973.
- 9 Ferenci Tamás cikke alapján.
- 10 Röst Gergely: A járványmatematikai és egyéb kutatások szerepe a koronavírussal szembeni védekezésben.
- 11 források: https://en.wikipedia.org/wiki/Basic_reproduction_number.
- 12 Az eredeti koronavírusra
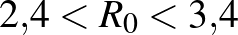 ; a variánsokra
; a variánsokra 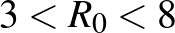 .
. - 13 forrás: https://vedooltas.blog.hu/2012/09/05/miert_oltunk_avagy_mire_jok_a_vedooltasok
- 14 Védett kétféleképp lehet valaki: védőoltás által vagy úgy, hogy már átesett a fertőzésen és immunissá vált a vírusra. (A fertőzésen való átesés nem minden esetben garancia az immunitásra.)
- 15 forrás: https://hu.wikipedia.org/wiki/Nyájimmunitás
- 16 Influenza esetén a járvány lefolyását az is befolyásolhatja, hogy a lakosság egyes csoportjait milyen sorrendben oltják be. Röst Gergely és Knipl Diána számításai alapján akár 10%-kal is csökkenthető az összes megbetegedett száma, ha influenzajárvány idején az iskolásokat oltják be először: http://www.epidelay.u-szeged.hu/images/readersdigest.png
- 17 A himlő esetében az egész világon elérték a kritikus átoltottsági szintet, így ez a betegség megszűnt 1979-ben.
- 18 A magasabb értékek a koronavírus új variánsaira vonatkoznak.
- 19 Egy 2019. decemberi cikk az európai kanyarójárványokról: https://www.magyarhirlap.hu/eletmod/20191209-meg-nem-csillapodott-a-kanyarojarvany-europa-szerte
- 20 Az Országos Epidemiológiai Központ 2012-es tájékoztatója az Ukrajnába utazni készülő focidrukkerek számára: https://index.hu/sport/futball/2012/04/21/kanyarojarvany_terjed_az_eb_elott_ukrajnaban/









