Haladás ellen nincs orvosság

Neumann János válogatott írásai (Bővített kiadás, szerk.: Ropolyi László, Typotex Kiadó, 2023) – fizikai, matematikai tárgyú írások

https://www.typotex.hu/book/13360/ropolyi_laszlo_neumann_janos_valogatott_irasai

Az Amerikai Matematikai Társaság (AMS) portréfilmeket készített híres matematikusokról; a Neumann Jánosról szóló epizódban a német származású amerikai Nobel-díjas fizikus, Hans Bethe elmeséli, hogy Princetonban az 1940–1950-es években körbejárt a szóbeszéd, miszerint Neumann koponyájában az emberi agynak valamely fejlettebb, azidáig nem tapasztalt képességekkel rendelkező ismeretlen mutációja rejtőzik. A feltételezést persze mindenki tréfának tekintette – de csak félig: aki személyes kapcsolatba került Neumannal, annak tényleg ez volt a benyomása róla. Félelmetes kapacitású és fotografikus memóriával rendelkezett; négy élő nyelven beszélt (sokszor egyszerre) és még latinul, ógörögül is; egészen kivételes munkabírással dolgozott és nagyrészt éjszaka; rendkívül nehéz matematikai problémákat gyakran villanásnyi idők alatt oldott meg: elterjedt, hogy egy olyan kérdést, amelyet Neumann János öt percen belül nem tud megválaszolni, nem is lehet megválaszolni stb.

Vitathatatlan, hogy a magyar származású amerikai matematikus Neumann János a XX. sz-i matematika, modern elméleti és alkalmazott fizika, közgazdaságtan, katonai stratégiaelmélet, elméleti és gyakorlati számítástudomány, röviden: az általános nyugati tudomány- és technikatörténet egyik kiemelkedő alakja. Szerteágazó tevékenysége, hatalmas intellektuális hagyatéka a XX–XXI. század arculatát több ponton is kritikusan befolyásolta, illetve befolyásolja: nehéz lenne megválaszolni, hogy az újra egyre reálisabb fenyegetést jelentő nukleáris fegyverek kifejlesztése, elterjedése és a hidegháború katonai startégiáinak („nukleáris elrettentés”) kidolgozása, vagy pedig az immár a globális mesterséges intelligencia kapujában álló elektronikus számítógépek megvalósítása gyakorol nagyobb hatást mindennapjainkra. De nemcsak folyamatok elindítója, következményeik előrelátója is volt: a túlnépesedés és a fokozódó globális környezetpusztítás, éghajlatváltozás okozta veszélyeket is megsejtve Neumann joggal tette fel a kérdést már 1955-ben híres dolgozata címében: Túlélhetjük-e a technikát?

Mindenesetre az biztos, hogy nagyon nehéz annak a szerkesztőnek a dolga, aki arra vállalkozik, hogy Neumann írásaiból, levelezéséből, vele készült interjúkból válogatva ne csak áttekintést adjon az életműről, hanem még Neumann személyesebb oldalát is valamennyire felvillantsa egy nem túl nagy terjedelmű könyvben. Erre a nehéz feladatra vállalkozott Ropolyi László, akinek szerkesztésében újra napvilágot látott Neumann válogatott írásainak bővített kiadása (Typotex, Budapest 2023). A kötet hat fejezetre oszlik: 1. A fizika alapjairól; 2. A matematika természetéről; 3. Számítógépek építésének és használatának problémáiról; 4. A matematikai közgazdaságtanról; 5. A technika, tudomány és társadalom kapcsolatáról; 6. Saját életkörülményeiről – ezekben az adott témakörrel kapcsolatos egy-egy tanulmány, könyvkivonat, levél, interjú olvasható. A recenzió első részében fizikai és matematikai témájú írásait (1–2. fejezet), illetve a modern kor problémáit (5. fejezet) taglaló dolgozatait tekintjük át.

Nem alaptalan a feltételezés, hogyha Neumann korai halála 1957-ben nem vet véget további kibontakozásának, akkor az elméleti fizika, matematika egyes igen nehéz területei – úgymint a kvantummechanika, a relativisztikus kvantummező-elméletek matematikai szerkezete, illetve interpretációs kérdései, valamint az áramlástanban a lökéshullámok leírása; matematikában pedig a halmazelmélet és a matematikai logika, az operátoralgebrák elmélete, valamint a nemlineáris parciális differenciálegyenletek numerikus megoldása – kb. húsz–huszonöt évvel fejlettebb és integráltabb alakjukban állnának előttünk, mint ahogy manapság ismerjük őket. Feltételezésünket néhány elfeledettnek tűnő neumanni gondolat felelevenítésével szeretnénk alátámasztani.

Fizika. Neumann több írásában is felhívja a figyelmet arra a túlságosan is megszokott és emiatt sokszor mellőzött tényre, hogy a klasszikus és modern fizika egyes elméleteinek léteznek különböző matematikai megfogalmazásaik. Jól ismert példa a klasszikus mechanika mint differenciálegyenletekre vonatkozó Cauchy-feladat, ill. mint a legkisebb hatás elvén alapuló kétlehetséges alakja. A két megfogalmazás matematikai értelemben szigorúan ekvivalens. Viszont fizikai értelemben nem, ugyanis az általuk „sugalmazott” fizikai világkép eltérő: az előbbi egy lokális-kauzális, míg utóbbi egy globális-teleologikus (célelvű) elvvel operáló univerzumot sejtet. A két leírás közötti választás nagymértékben önkényes, szigorú módszerekkel bármelyiket kitüntetni nem lehet. A kvantummechanika egy sokkal bonyolultabb kurrens példa. Három megfogalmazása is ismert: a Heisenberg-féle mátrixmechanika, a Schrödinger-féle hullámmechanika;– ezek egy időben születtek meg –, és a Feynman-féle pályaintegrálos alak, ami későbbi. E megfogalmazások matematikailag mind precízek és ekvivalensek, tehát a kvantummechanika matematikailag nagyon erős lábakon áll. Viszont a fizikai jelentése körül immár száz éve tartó, szűnni nem akaró vita zajlik. A korszerű tudományelméleti definíció szerint egy fizikai elmélet olyan, a természet valamilyen szempont szerint egybetartozónak vélt jelenségeit leíró kétszintű struktúra, amelynek első szintaktikai szintjén egy matematikai modellt fogalmazunk meg, és ebben a matematika szigorú formális szabályai szerinti tevékenységet végzünk („számolunk”); második, szemantikai szintjén pedig a modell egyes matematikai fogalmainak fizikai jelentéssel bíró felruházását, vagyis a természeti jelenségekre való visszavonatkoztatását végezzük el („fizikai interpretáció”). Egy kidolgozott fizikai elmélet szintaktikai szinten mindig lezárt-befejezett, szemantikai szinten viszont mindig nyitott-kibontakozó.¹ Tehát a kvantummechanika körüli inerpretációs vita abból áll, hogy a fizikai elmélet egy partikuláris szintaktikájában feltárt matematikai struktúrák mind megjelennek-e szemantikai szinten is? És ha igen, miféle fizikai jelentéssel bírnak? De először is: melyik matematikai modellt válasszuk a fizikai interpretáció tárgyául? Neumann A módszer a fizikában c. 1945-ben megjelent tanulmányában ezt írja (l. 78. old.):

De mindvégig teljesen világos volt, hogy azt, hogy az egyik vagy a másik elméletet [értsd: modellt – E.G.] választják, végső soron az motiválja, hogy a kvantummechanika minden sikere ellenére olyan területekkel határos, amelyeken az elmélet nem kielégítő, nevezetesen az elektrodinamika kvantumelméletével és ennek következtében az olyan részecskék, mint a mezonok kvantumelméletével.

Utóbbiakról jóval kevesebbet tudunk, mint a kvantummechanika eredeti területéről, és itt súlyos nehézségek közé kerültünk. Az ok, amely miatt a kvantumelmélet egyik változatát előnyben részesítették a másikkal szemben, általában az az intiutív remény volt, hogy az egyik vagy a másik fog jobb heurisztikus útbaigazítást adni az elmélet kiterjesztésére azokra a területekre, amelyek még nem kielégítően megmagyarázottak vagy nem kifogástalanul általánosítottak és ellenőrzöttek. Az utóbbi húsz évben az a felfogás uralkodott, hogy minden azon múlik, sikerül-e megtalálni az elmélet korrekt formális kiterjesztését. Ha végül is bebizonyosodik, hogy valóban ez a helyzet, az el fogja dönteni a végső választást. A formai kérdéseknek tehát nagy heurisztikus és útbaigazító jelentőségük lehet még akkor is, ha a matematikai összefüggések ekvivalensek, és végül is ezek dönthetik el a végeredményt.

Meglepő, és a fizika, illetve a matematika sokkal mélyebben megbúvó és talán közös tőről fakadó problémáira utal, hogy a kvantummechanika Neumann által is fontosnak tartott térelméleti kiterjesztését matematikailag precíz alakban – az azóta eltelt, immár száz év alatt – sem sikerült elvégezni. Mindössze annyi állapítható meg, hogy e kiterjesztési törekvésekben inkább a Heisenberg-, illetve a Feynman-féle formalizmusok ígéretesek, ugyanis kiderült, hogy a Schrödinger-féle megfogalmazás, különös tekintettel annak Born-féle valószínűségi interpretációjára, nem használható jól (leginkább azért, mert a Schrödinger-féle 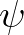hullámfüggvény Dirac-féle relativisztikus általánosításában az antirészecskék elkerülhetetlen felbukkanása miatt bizonyos 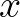téridő-pontokban már 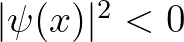is megengedett, ami lehetetlenné teszi a valószínűségi értelmezést). Ez azt sugallja, hogy habár szintaktikailag ekvivalensek, a Heisenberg-, illetve a Feynman-formalizmus szemantikai szinten „közelebb állhat” a kvantumelmélet egyelőre ismeretlen mélyszerkezetéhez, mint a Schrödinger-féle. Ennek dacára Neumann halála óta, tehát az utóbbi évtizedekben a kvantummechanika hullámmechanikai megfogalmazása folyamatosan kiszorította a többit mind a régóta gyakorló fizikusok, mind a kvantumelmélet területére újonnan belépő filozófusok körében; ez talán indokolt matematikai-számoláskivitelezési-praktikus okokból azonban nem teljesen érthető a kvantummechanika egészét illetően. És ennek megfelelően az elmélet interpretácója körüli egyre parttalanabb vitákat is mindjobban pusztán a Schrödinger-megfogalmazásban szereplő matematikai objektumok fizikai jelentésének tisztázása tölti ki, különös tekintettel a „hullámfüggvényre” és annak viselkedésére mérési folyamatok során.

Matematika. Talán ars poetica is lehetne Neumann azon egész munkásságán átívelő meggyőződése, hogy a matematika nem választható le tapasztalati eredetű gyökereiről. Ezt hangsúlyozza például A matematikus c. 1947-ben megjelent esszéjében is (l. 99–100. old.):

Ha egy matematikai diszciplína messzire távolodik tapasztalati forrásától, vagy még inkább, ha már a második vagy harmadik nemzedéket csak közvetve érik el a „valóságból” származó eszmék, ez súlyos veszélyt rejt magában. Egyre inkább tiszta esztétizálássá válik, egyre tisztább l'art pour l'art-rá. Ez nem feltétlenül rossz, ha a területet csatlakozó tárgyak veszik körül, amelyek még szorosan kapcsolódnak a tapasztalathoz, vagy ha a tudományág kivételesen fejlett ízlésű emberek befolyása alatt áll. De súlyos a veszély, hogy a tárgy a kisebb ellenállás irányába fejlődik, hogy a forrástól eltávolodott folyó jelentéktelen ágak sokaságává különül el, és a diszciplína részletek és bonyodalmak szervezetlen tömegévé válik. Más szóval, a tapasztalati forrástól nagy távolságban vagy sok „absztrakt” behatás után a matematikai tárgyat a degenerálódás fenyegeti. Kezdetben a stílus rendszerint klasszikus, amikor azonban a barokká válás jelei mutatkoznak, a vészjelzés adott.

A modern matematika legjelentősebb tapasztalati forrása a fizika. Ezért ha a fentebb megkezdett fizikai ösvényen haladunk tovább, a matematikai részt is döccenés nélkül tekinthetjük át Neumann szellemében. Érdekes egybeesés, hogy a fizika és a matematika szinte egyszerre élte át eddigi történetének legnagyobb válságait a XIX–XX. század fordulóján. Neumann így ír erről (l. A módszer a fizikában, 71. old.):

Két ilyen válság a fizikában volt: a fogalmi átrendeződés a relativitás elvének felfedezésével kapcsolatban, valamint a fogalomalkotás nehézségei a kvantumelméleti felfedezésekkel kapcsolatban. A relativitáselmélettel kapcsolatos krízis rövid volt, de éles. A másik válság hosszú időn át tartott, a kvantumelmélet kialakulásának majdnem harminc évén át.

A harmadik válság a matematikában zajlott. Ez nagyon komoly fogalmi válság volt, a szigorra és a korrekt matematikai bizonyítás helyes módjára vonatkozott. A matematika abszolút szigorára vonatkozó régebbi nézetek fényében meglepő, hogy ilyesmi megtörténhetett, és még meglepőbb, hogy napjainkban következett be, amikor már nem hiszünk a csodákban. Mégis bekövetkezett.

Neumann azon kevesek közé tartozott, akik két krízis lezajlását is közelről figyelhették, sőt, a kvantummechanika fogalmi, illetve a matematika jólmegalapozottsági problémáinak vizsgálatában jelentős szerepet is játszott. Látott-e valamilyen kapcsolatot a két problémakör között? A matematika szerepe a tudományokban és a társadalomban c. 1954-ben megjelent dolgozatában a matematikában felbukkant váratlan nehézségekkel kapcsolatban ezt írja (l. 105. old.):

[] megjegyzem, hogy mindez azzal az igen bonyolult ismeretelméleti kérdéssel kapcsolatos, hogy jogosult-e nem véges számú egységek összességét vizsgálni; vagy hogy matematikai fogalmak végtelen összességével foglalkozva, pontosan mit jelent az, ha általános állítást kockáztatunk meg, pontosan mit jelent az, ha azt mondjuk, hogy tudjuk, hogy valami lehetséges egy ilyen összességben? Azt jelenti-e, hogy van egy tényleges példánk? Azt jelenti-e, hogy van valamilyen más módszerünk, hogy megmutassuk: létezik egy ilyen példa? Mármost valójában van-e bármilyen mód arra, hogy egy példa létezését bizonyítsuk anélkül, hogy részletesen bemutatnánk? Valamennyiünk számára az egyik nagy meglepetés az volt, hogy kiderült: a matematika általánosan elfogadott módszerei ténylegesen olyanok, hogy léteznek fogások, amelyekkel bizonyítható egy példa anélkül, hogy azt bemutatnánk. Nem könnyű elképzelni, hogyan történhet ez meg. De valóban megtörtént, és ez a normális matematikai gyakorlat.

Azt szeretném tehát mondani, hogy van itt néhány nagyon nehéz és kényes kérdés, s az ember nem kerülheti el a következtetést, hogy ezek bizonyos fokig hasonlóak a fizika alapjait érintő kérdésekhez. Lehetséges, hogy valamit kézenfekvőnek érzünk, és ez valamilyen módon a kényelemmel függ össze, és hogy szó sincs arról az emberfeletti, abszolút megbízhatóságról, amelyet a matematika egyik lényeges elemének tartanak. Van tehát a kétségnek bizonyos tere itt; s a matematika jellegét és szerepét értékelve nem szabad megfeledkeznünk arról, hogy a kétség létezik.

A Neumann által említett matematikai létezést garantáló „fogások” listáján valószínűleg szerepel a XX. sz-i matematika fenegyereke, a kiválasztási axióma. Alkalmazásával a valós számokról olyan kijelentések tehetők, mint például a Banach–Tarski paradoxon. Az 1930-as években (Tarskiék és Neumann fiatalkorában) a Banach–Tarski-paradoxon érv volt a kiválasztási axióma ellen: a kiválasztási axiómával mindenfajta konstruktív útmutatás nélkül ex cathedra posztuláljuk megfoghatatlan, elképzelhetetlen objektumok létezését, és ennek olyan kontraintuitív következményei vannak, amelyek ellentmondanak az „anyagmegmaradásnak”. Azt gondolták, nagyon óvatosnak kell lennünk az olyan állításokkal, amelyek bizonyos objektumok létezését úgy posztulálják, hogy nem adnak módszert a kérdéses objektumok előállítására, mert lám, ezeknek olyan következményeik lehetnek, amelyek a szemléletünknek élesen ellentmondanak. Azóta a Banach–Tarski paradoxont megértették, és a kiválasztási axióma helyet kapott a „hétköznapi” matematikában.² Viszont ha a Neumann által szintén említett kétség a matematika megbízhatóságával szemben továbbra is fennáll, akkor fel kell tenni a kérdést: mennyire bízhat meg egy fizikus például abban a matematikai struktúrában, amellyel a fizikai időt és teret modellezik a jelenkori fizikában? Ez a XIX. században megkonstruált struktúra ugyanis nem más, mint a valós számok halmaza. Paradox tulajdonságait részben már ismerve megbízhatóan fog-e teljesíteni olyan extrém szituációkban is, mint például egy atommag mélye, egy fekete lyuk belseje vagy az Ősrobbanás utáni első 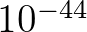másodperc fizikai körülményei? Egyelőre nem teljesen tisztázott okoknál fogva a kvantummechanika ezekre a helyzetekre vonatkozó kiterjesztései immár száz éve matematikailag stabilan inkonzisztensek.

Meg kell még említeni, hogy azért sok olyan, Neumann által elindított kutatási irány is van, ahol az utóbbi fél évszázadban jelentős előrehaladás történt. Ilyen például az operátoralgebrák elmélete, amely szintén szorosan kapcsolódik a modern fizikához (és a fentebbi kérdésekhez is). A terület 1940–1950-es évekbeli állapotának áttekintését adja Neumann előadása, amelyet az 1954. évi Nemzetközi Matematikai Kongresszuson tartott Megoldatlan problémák a matematikában címmel (l. 114–136. old.).

Technikai fejlődés és a jövő. Habár e sorok írója szakmailag kívülállónak tekinti magát olyan szerteágazó komplex kérdések vizsgálatában, mint például hogy az egyre gyorsuló technikai fejlődés a túlnépesedéssel és a globális környezeti problémákkal megtoldva merre alakítja jövőnket, mégsem tekintheti magát kívülállónak olyasvalakiként, mint aki ebben az egész problémahalmazban kénytelen részt venni. Ezért következzék itt egy rövid megjegyzés, amely tehát elismerten szubjektív.

A második világháború idejétől kezdve szaporodnak az olyan elemzések, amelyek egy egyre magasabb technikai fejlettségű és túlnépesedő, ugyanakkor vallási-ideológiai-nemzeti stb. vonalak mentén egy egyre inkább széttöredező világ növekvő külső-belső instablitására hívják fel a figyelmet. Ezek közé tartozik Neumann 1955-ben megjelent Túlélhetjük-e a technikát? c. dolgozata is (l. 361–374. old.).³ Az elemzések szemléletmódja az idő múlásával a kezdeti, úgynevezett „objektív”, „elkerülhetetlen” okok és mechanizmusok – például Neumann dolgozatában szerepel az elhíresült mondat: A haladás ellen nincs orvosság⁴ stb. – feltárásától érzékelhetően tolódik el a multinacionáis cégek profitmaximalizálási törekvéseinek, majd az „emberi, túlságosan is emberi” tényezők: az élvhajhászatban és a tömegfogyasztásban vidáman lubickoló átlagfogyasztó személyes szerepének hangsúlyozása felé. És tényleg: például mi célból égettük el, mire használtuk el a kőszenet, kőolajat, a földgázt az elmúlt száz év során? Mi volt az a nagyszerű eszme, az a nagyszabású cél, amiért az utókor majd azt mondja rólunk: ezért még a környezetszennyezés, az éghajlatváltozás is megérte? A korszerű mezőgazdaság rengeteg szénhidrogént használ el egyrészt talajművelésre, másrészt intenzív műtrágyázás formájában; talán a gyors és olcsó közlekedés megszületésének is lehetne örülni, az ezzel együttjáró tömegturizmusnak már nem annyira. De legnagyobbrészt olyan egyszer használatos, ugyanakkor nem lebomló műanyag termékek előállítására fordítottuk forrásainkat, amelyek mindent elárasztó maradékaival (vagyis a műanyagszeméttel) most nem tudunk mit kezdeni. Mindez pedig egy remek ötlet: a tervezett elavulásnak nevezett gazdasági doktrína keretében zajlik például úgy, hogy egyes nagy autógyártók (a politikusok jóváhagyásával) évtizedek óta manipulálják az emisszióval kapcsolatos adataikat (l. német dízelbotrány), vegyipari óriásvállalatok pedig saját kutatásaik alapján már az 1980-as évek eleje óta jól tudják, hogy a műanyagok újrahasznosítása fenntartható formában (jelenlegi ismereteink szerint) nem lehetséges. Ami pedig minket illet, valljuk be, hogy a jövővel kapcsolatos, úgynevezett „rémisztő kilátások” ellenére a reklámoknak továbbra sem túl nagy erőfeszítés újabb céltalan utazásokra, túlfogyasztásra stb. buzdítani bennünket. Az efféle haladásra persze tényleg nincsen orvosság.

Zárásképpen néhány észrevétel a kötettel kapcsolatban. A Gondolat Kiadó Válogatott tanulmányok címmel sorozatot jelentetett meg híres XX. századi természettudósok népszerűsítőbb írásaiból nagyjából 1960 és 1990 között. E sorozatból érthetetlen módon hiányzik a Neumann Jánosról szóló kötet.⁵ Már emiatt is várva várt hiánypótlásnak kell tekinteni a most megjelent könyvet. A Gondolat sorozatán végigvonuló szerkesztői elképzelés az volt – habár nem mindig teljesült – hogy lehetőleg teljes tanulmányokat, előadásokat, rövidebb könyveket, teljes levelezéseket mutassanak be. Így ugyan kevesebb minden fért egy kötetbe, de az olvasónak megvolt az a jóleső érzése, hogy egyrészt tisztázott volt a szövegbeli matematikai jelölésrendszer, másrészt lekerekített, zárt, egész gondolatmenetekkel ismerkedhetett meg. A kivételesen szerteágazó Neumann-életmű esetében az elv alkalmazása nyilván nehezebb lehetett, s talán ezzel magyarázható, hogy a mostani Neumann-válogatásban sok részlet, kivonat, válaszok nélküli levél olvasható. Úgy éreztük, hogy ez nem tett igazán jót a válogatásnak. Például a kötet nyitó tanulmánya, Neumann A kvantummechanika matematikai alapjai (Akadémiai, Budapest 1980) c. könyvének részlete, kiragadottnak tűnik abban az értelemben, hogy még a Neumann által használt matematikai jelölések sem tisztázottak benne (természetesen a Neumann-könyvben minden precízen be van vezetve). Meglehetősen váratlanul szakad egyszer csak félbe Az EDVAC-ról szóló jelentés első vázlata c. tanulmány (l. 149–174. old.), illetve a Neumann–Morgenstern-könyv bevezetés-részleténél (l. 329–355. old.) hirtelen magunkra maradva is azt kérdeztük: miért pont itt? Továbbá számunkra nem volt teljesen világos az egyes fejezetek végén néhány kissé ad hoc tárgyúnak tűnő levél közlése mögött megbújó szerkesztői szándék sem.

Végül ezúton is köszönet Sági Gábornak (RI, Halmazelmélet, Logika és Topológia Oszt., BME MI, Algebra és Geometria Tsz.) néhány matematikai kérdés tisztázásában nyújtott segítségéért.

Lábjegyzetek

¹Erre mondja Richard Feynman A fizikai törvények jellege c. könyvecskéjében (Magvető, Budapest 1983), hogy egy megfelelően mély fizikai elmélet mindig „valahogyan több” mint bármelyik matematikai modellje.

²A mai szóhasználatban az „axióma” valamiféle megváltoztathatatlan, kőbe vésett igazságot jelent. Pedig Szabó Árpád szerint a görög eredetiben mindössze „méltányos kérést” jelenthetett („axiosz” görögül: „méltó”). Így ír A görög matematika kibontakozása (Magvető, Budapest 1978) c. tanulmányában (l. 213–214. old.): „Nyilván erre a hangsúlyozni akart jelentésárnyalatra vezethető vissza az is, hogy később az axiómákat görögül inkább a „koinai ennoiai” kifejezéssel írták körül. (Így nevezik az axiómákat a ránk maradt Euklidész-kéziratok.) Ezt az utóbbi körülírást latinul „communes animi conceptiones”-nek mondják –- ezzel fejezvén ki azt, hogy az axiómák „közös lelki alkatunknak megfelelő állítások”.

³További könyvek a legkülönbözőbb területekről a teljesség lehetősége nélkül: J. O.  y Gasset 1928-as könyve: A tömegek lázadása (Helikon, Budapest 2019); N. Wiener 1950-es könyve: Human use of human beings (in: N. Wiener: Válogatott tanulmányok, Gondolat, Budapest 1974); C. G. Jung 1952-es könyve: Válasz Jób könyvére (in: C. G. Jung Összegyűjtött Munkái 11, Scolar, Budapest 2005); A. C. Clarke 1962-es könyve: A jövő körvonalai (Gondolat, Budapest 1969); H. Marcuse 1964-es könyve: Az egydimenziós ember (Kossuth, Budapest 1990); S. Lem 1967-es könyve: Summa technologiae (Kossuth, Budapest 1972); E. F. Schumacher 1980-as könyve: A kicsi szép (Közgazdasági, Budapest 1991); K. Lorenz 1988-as könyve: Ember voltunk hanyatlása (Cartafilus, Budapest 1996); E. Drewermann: Der tödliche Fortschritt (Herder, Freiburg 1991); S. P. Huntington 1994-es könyve: A civilizációk összecsapása és a világrend átalakulása (Európa, Budapest 1998); J. Diamond: Collapse (Penguin Books, New York 2005); Gelencsér András: Ábrándok bűvöletében (Akadémiai, Budapest 2023) stb.

⁴Angolul: For progress there is no cure, a könyvben magyarul úgy szerpel, hogy A fejlődés ellen nincs gyógymód (l. 373. old.).

⁵Neumann János: Válogatott tanulmányok és előadások a Közgazdasági és Jogi Könyvkiadónál jelent meg 1965-ben, de messze nem tekinthető minden területre kiterjedő válogatásnak.