1. Bevezető megjegyzések
Neumann János tudományos munkásságának lényeges részét alkotják a kvantummechanika alapjainak területén folytatott vizsgálódásai. Lax Péter megítélése szerint Neumann Jánosnak ezen a területen elért eredményei fizikai Nobel-díjra érdemesítenék őt [11]. A terület iránt Neumann érdeklődése egész tudományos munkássága során megmaradt: A kvantummechanika alapjaival foglalkozó első (társszerzős) cikke 1928-ban jelent meg [10], és még 1954-ben is ezt a témát választotta elemzésre, amikor felkért előadást tartott a Nemzetközi Matematikai Kongresszuson [43], [18].
Neumann e területen végzett munkásságával kapcsolatban meg kell különböztetni két vonatkozást: egyfelől a kvantummechanika matematikai alapjainak tisztázásával kapcsolatos tisztán matematikai eredményeket, másfelől a kvantummechanika fogalmi-fizikai (és sokszor kifejezetten és tudatosan filozófiai) értelmezésére vonatkozó meggondolásokat. Ez a két vonatkozás azonban nem független. Neumann matematikai munkásságát általában is, de különösen a kvantummechanika számára fontos funkcionálanalízis területén, közvetlenül motiválták az empírikus tudományok problémái: Neumann úgy gondolta [44], hogy a matematika legabsztraktabb fogalmai is az empirikus tudományok azon igényéből fakadnak, hogy a tudományuk tárgyát kvantitatívan leírják. Ez a kvázi-empírikus matematikafelfogás ma sem univerzálisan elfogadott, sem a matematikusok, sem az elméleti fizikusok között. Neumann kortársai közül pl. sem Wigner, sem Gödel nem osztotta ezt a nézetet. (Neumann empírikus matematikafelfogásáról, és ennek a Wigner és Gödel által képviselt felfogásokhoz való viszonyáról a [20], [24], [6] és [25] dolgozatokban lehet bővebben olvasni).
Mivel Neumann matematikai eredményei a kvantummechanika matematikai alapjaival kapcsolatban nagyon szerteágazóak és összetettek, ez az írás csak arra tud vállalkozni, hogy azokat a legfontosabb neumanni eredményeket említse meg, amelyek a kvantummechanika általános matematikai szerkezete szempontjából lényegesek. Ez az általános matematikai szerkezet a nemkommutatív valószínűségszámítás.
Neumann munkássága ebből a szempontból két korszakra osztható: az első korszak az 1928–1932 közötti időszak. Neumann eredményei ebben az időszakban a kvantummechanika Hilbert-tér formalizmusának matematikai alapjait hozták létre. A második korszak az 1935 utáni idő. Ez utóbbi szakaszban az operátorgyűrűk (mai nevükön: Neumann-algebrák) elméletének megalkotásával jött létre a nemkommutatív mértékelmélet. A Neumann-algebrák elméletének keretei között nemkommutatív valószínűségi mértékterek léteznek. Ezek olyan kvantumfizikai rendszereket írnak le, amelyeknek leírása nem lehetséges a Hilbert-tér formalizmus nyújtotta nemkommutatív valószínűségszámítás keretei között.
E két korszakot megelőzi egy nagyon rövid periódus, amikor Neumann Hilberttel Göttingenben dolgozott egy a kvantummechanika alapjaival foglalkozó közös publikáción. A 2. fejezet röviden kitér erre a munkára. A 3. fejezet Neumannak a Hilbert-tér formalizmushoz való hozzájárulását foglalja össze, a 4. fejezetben Neumann néhány fontosabb gondolatát a Neumann-algebrák kvantummechanikai jelentőségével kapcsolatban említjük meg.
2. Az 1928-as Hilbert–Neumann–Nordheim-dolgozat
A [10] cikk Hilbert Göttingenben tartott előadásain alapul. A dolgozat két okból figyelemreméltó. Először amiatt, mert ez az első kísérlet a kvantummechanika axiomatikus felépítésére abban a szellemben, ahogyan Hilbert a fizikai elméletek axiomatizálásának programját megfogalmazta híres, Párizsban 1900-ban, a matematika legfontosabb nyílt problémáiról tartott előadásában [9] [49]. Nem nyilvánvaló azonban, hogy mit jelent axiomatikusan felépíteni egy természettudományos elméletet. Ennek megfelelően, az 1928-as cikkben a szerzők expliciten megfogalmazzák, mit értenek axiomatikus módszeren a fizikában. Erről az „opportunista, puha axiomatizmus”-nak nevezett axiomatizmusról a [21], [27] dolgozatokban lehet részleteket olvasni.
Az 1928-as cikk másik fontos tulajdonsága, hogy annak ellenére matematikailag nem kifogástalan, hogy a korszak vezető matematikai folyóiratában jelent meg. A szerzők ezzel teljesen tisztában vannak, amit jól mutat, hogy a dolgozat végén explicite meg is fogalmazzák ezt:
„Azonban az itt elvégzett számítások matematikai szempontból […] meglehetősen nem-kielégítőek, mert sosem lehetünk biztosak abban, hogy az előforduló műveletek milyen mértékben megengedettek. Emiatt további részletezésüktől eltekintünk. Reméljük azonban, hogy egy más alkalommal visszatérhetünk ezekre a kérdésekre.” [10][30. old.]
És valóban: Neumann visszatér ezekre a kérdésekre, és tisztázza őket három alapvető fontosságú dolgozatban, amelyekben már egyedüli szerző [36], [38], [37]. Ezek a cikkek azok, amelyekben matematikailag kielégítő formában jelenik meg az, amit a mai napig a „kvantummechanika Hilbert-tér fomalizmusának” hívunk. Ez a három cikk az alapja Neumann 1932-ben megjelent könyvének [41], ami a Hilbert-tér formalizmusnak első szisztematikus és matematikailag precíz összefoglalása.
3. 1928–1932: Neumann hozzájárulása a kvantummechanika Hilbert-tér formalizmusának kidolgozásához
Mai terminológiában és modern jelölésben a kvantummechanika Hilbert-tér formalizmusa matematikai szempontból egy speciális típusú nemkommutatív valószínűségelmélet [28]. Ez azt jelenti, hogy a klasszikus, Kolmogorov-féle valószínűségi mértéktér 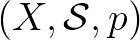 helyébe (ahol
helyébe (ahol 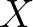 az elemi események halmaza,
az elemi események halmaza, 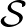 egy Boole-algebra
egy Boole-algebra 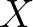 -en,
-en, 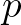 valószínűségi mérték
valószínűségi mérték 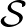 -en) a
-en) a 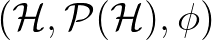 struktúra lép, ahol
struktúra lép, ahol

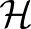 egy absztrakt (komplex) Hilbert-tér,
egy absztrakt (komplex) Hilbert-tér,

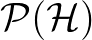 a
a 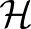 Hilbert-tér projektorhálója (Hilbert-háló),
Hilbert-tér projektorhálója (Hilbert-háló),

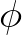 egy
egy 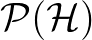 -n értelmezett additív mérték a
-n értelmezett additív mérték a ![$[0,1]$](/images/stories/latexuj/2023-05/2023-05-neumannjanosmunkassaga/img10.png) intervallumba.
intervallumba.
Továbbá:
 A klasszikus (valós értékű) véletlen változók kvantumos megfelelői a projektormértékek: az
A klasszikus (valós értékű) véletlen változók kvantumos megfelelői a projektormértékek: az 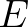 Boole-algebra homomofizmusok a valós számok Borel-halmazalgebrájából a
Boole-algebra homomofizmusok a valós számok Borel-halmazalgebrájából a 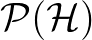 projektorhálóba.
projektorhálóba.
 Minden projektormértéknek megfelel egy (nem föltétlenül korlátos) önadjungált operátor és fordítva: Minden
Minden projektormértéknek megfelel egy (nem föltétlenül korlátos) önadjungált operátor és fordítva: Minden 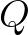 önadjungált operátor meghatároz egy
önadjungált operátor meghatároz egy 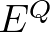 projektormértéket („Spektráltétel”).
projektormértéket („Spektráltétel”).
 Minden
Minden 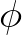 kvantumállapot
kvantumállapot 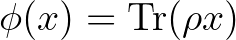 alakú egy nemnegatív, egységnyomú
alakú egy nemnegatív, egységnyomú 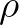 operátorral (sűrűségmátrix) („Gleason-tétel”).
operátorral (sűrűségmátrix) („Gleason-tétel”).
Ezt a valószínűségelméletet azért hívjuk nemkommutatívnak, mert a projektorok szorzása nemkommutatív művelet, és a Hilbert-háló kommutatív projektorok által generált részhálója disztributív részháló (Boole-algebra).
Ennek a matematikai struktúrának a fizikai interpretációja: Ha a fizikai rendszer a 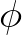 -vel leírt állapotban van, akkor annak valószínűségét, hogy a
-vel leírt állapotban van, akkor annak valószínűségét, hogy a 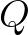 operátorral reprezentált fizikai mennyiség értéke a
operátorral reprezentált fizikai mennyiség értéke a 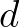 valós Borel-halmazba esik, a következő formula adja meg:
valós Borel-halmazba esik, a következő formula adja meg:
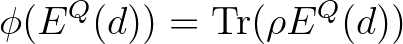 |
(1) |
Az itt leírt Hilbert-tér formalizmus kulcsfontosságú fogalmait és eredményeit (kivéve a Gleason-tételt) Neumann alkotta meg: Neumann első dolgozata [36] létrehozta az absztrakt Hilbert-tér fogalmát, axiomatikusan rögzítve a konkrét Hilbert-tereket alkotó függvényterek lényeges strukturális-geometriai tulajdonságait (megkövetelve még az absztrakt Hilbert-terektől a szeparabilitást is – ezt ma már nem tekintjük a Hilbert-tér definíciója részének). A [36] cikk, és az ebben már idézett, de csak később megjelent [39] dolgozat lényegében megalkotja a projektormérték fogalmát, és bebizonyítja a spektráltételt.
A [38], [37] dolgozatok további fontos eredményei:
(i) A tiszta kvantumállapotok definíciója és annak megmutatása, hogy az egydimenziós projektorok mint sűrűsegmátrixok adják a tiszta állapotokat.
(ii) Egy Hamilton-operátorhoz és véges hőmérséklethez tartozó Gibbs-állapot definíciója.
(iii) A sűrűségmátrix entrópiájának (kvantumentrópia) bevezetése és ezáltal a kvantumstatisztikus mechanika alapjainak megalkotása.
Könyvében [41] Neumann továbbá megmutatja, hogy a tiszta kvantumállapotok sem szórásmentesek: nem igaz, hogy 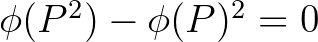 minden
minden 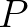 projektorra, akkor sem, ha
projektorra, akkor sem, ha 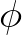 tiszta állapot. Emiatt nem lehetséges úgy gondolni a kvantumállapotokra, hogy azok szórásmentes állapotok kombinációi – ellentétben a klasszikus valószínűségszámítással, ahol az összes valószínűségi mértékek konvex halmazának extremális pontjai 0-1 értékű (azaz szórásmentes) mértékek. Ezt a tényt Neumann úgy értelmezi, hogy nem léteznek „rejtett paraméterek” – olyan fizikai mennyiségek, amelyek értékeinek rögzítésével fizikai rendszerek olyan statisztikus sokaságát lehet létrehozni, amelyekben a kvantum-megfigyelhető mennyiségek mindegyikének éles értéke van. Neumann ezen értelmezése kiindulópontja lett egy szerteágazó, ellentmondásos, a kvantummechanika alapjait, értelmezését illető filozófiai színezetű kutatásnak, amelynek főbb irányait áttekinteni már 50 éve is csak egy könyvben lehetett [2] (egy nagyon rövid összefoglalást ad [17] 9. fejezete).
tiszta állapot. Emiatt nem lehetséges úgy gondolni a kvantumállapotokra, hogy azok szórásmentes állapotok kombinációi – ellentétben a klasszikus valószínűségszámítással, ahol az összes valószínűségi mértékek konvex halmazának extremális pontjai 0-1 értékű (azaz szórásmentes) mértékek. Ezt a tényt Neumann úgy értelmezi, hogy nem léteznek „rejtett paraméterek” – olyan fizikai mennyiségek, amelyek értékeinek rögzítésével fizikai rendszerek olyan statisztikus sokaságát lehet létrehozni, amelyekben a kvantum-megfigyelhető mennyiségek mindegyikének éles értéke van. Neumann ezen értelmezése kiindulópontja lett egy szerteágazó, ellentmondásos, a kvantummechanika alapjait, értelmezését illető filozófiai színezetű kutatásnak, amelynek főbb irányait áttekinteni már 50 éve is csak egy könyvben lehetett [2] (egy nagyon rövid összefoglalást ad [17] 9. fejezete).
Neumann eredményei kiküszöbölték az 1928-as dolgozatban [10] megfogalmazott axiomatizálás matematikailag nem kielégítő voltát, amely a Hilbert-téren értelmezett nemkorlátos lineáris önadjungált operátorok spektrálelméletének kidolgozatlanságából fakadt. Azon operátorok némelyike (pl. energia, helyzet, impulzus) amelyek fontos fizikai mennyiségek matematikai reprezentánsai, nem korlátos, és spektrumuk tartalmaz olyan valós számokat, melyek nem sajátértékek. Emiatt az ilyen operátorokkal való műveletek, és speciálisan ezen operátorok spektrális felbontásának meghatározása nem egyszerű, nehéz feladat. A matematikailag nem precíz elméleti fizikában ezt a problémát Neumann korában úgy kezelték, hogy megengedtek „nem igazi” sajátértekeket, amelyekhez „nem igazi” sajátfüggvények tartoznak. Ilyen volt a Dirac-féle delta függvény, ami nem volt matematikailag értelmes objektum. A kvantummechanika tehát lényegében matematikai ellentmondásokat tartalmazott. Ezeket az ellentmondásokat Neumann eredményei kiküszöbölték a kvantummechanikából.
4. Túl a Hilbert-tér formalizmuson
Nem sokkal a kvantummechanika Hilbert-tér formalizmusát összefoglaló könyvének megjelenése után Neumann arra az álláspontra jutott, hogy a Hilbert-tér formalizmus nem a legalkalmasabb matematikai keret a kvantummechanika számára. Ezt expliciten megfogalmazta Birkhoffhoz (minden valószínűség szerint 1935-ben írt) írt levelében:
„Szeretnék egy vallomást tenni, ami erkölcstelennek tűnhet: Már nem hiszek teljesen a Hilbert-térben.” [47]
Sokrétűek az okai annak, hogy Neumann elvesztette a hitét a Hilbert-tér formalizmusban. Ezekben a technikai és interpretációs vonatkozások szorosan összefonódnak, ezekről részletesen a [16], [23], [19] dolgozatokban lehet olvasni. A történeti részletek mellőzésével, összefoglalásszerűen a következőket lehet mondani arról, hogy mai szempontból visszatekintve mi annak a lépésnek a matematikai tartalma és jelentősége, amit Neumann tett akkor, amikor a kvantummechanika Hilbert-tér formalizmusától eltávolodott 1935-ben.
Neumann 1935-ben már dolgozott az operátorgyűrűk (mai nevükön: Neumann-algebrák) elméletén J. Murray-vel. A Neumann-algebrák egy Hilbert-téren értelmezett összes korlátos lineáris operátorok algebrájának olyan részalgebrái, melyek zártak egy olyan topológiában, amely gyengébb mint az uniform topológia. Az ilyen algebrákkal kapcsolatos eredményeket négy (ma már klasszikus) cikkben publikálták [12], [13], [42] [14]. Ezeknek a cikkeknek a jelentősége a kvantummechanika – illetve általánosabban a fizika – számára az, hogy a Neumann-algebrák elmélete nemkommutatív mértékelméletül szolgál, amelynek keretein belül különböző típusú nemkommutatív valószínűségi mértékterek léteznek – hasonlóan ahhoz, ahogy a klasszikus mértékelmélet keretéül szolgál a klasszikus valószínűségelméletnek a valószínűségelmélet Kolmogorov-féle axiomatizálásában. A „típus” itt úgy értendő, hogy a véges-végtelen és diszkrét-folytonos jelzőpárok négy lehetséges kombinációjából adódó négyfajta klasszikus mértéktértípusnak a nemkommutatív megfelelőjét alkotják a Murray–Neumann-osztályozás szerinti különböző típusú (faktor) Neumann-algebrák. Az alábbi táblázat mutatja ezeket a klasszikus mértéktér típusokat, az utolsó oszlopban a megfelelő Murray–Neumann-típusokkal:
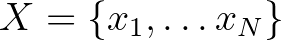 , , |
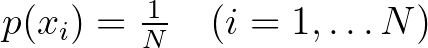 |
diszkrét, véges | I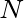 |
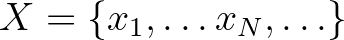 , , |
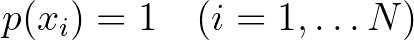 |
diszkrét, végtelen | I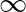 |
![$X=[0,1]$](/images/stories/latexuj/2023-05/2023-05-neumannjanosmunkassaga/img26.png) , , |
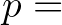 Lebesgue-mérték Lebesgue-mérték ![$[0,1]$](/images/stories/latexuj/2023-05/2023-05-neumannjanosmunkassaga/img10.png) -en -en |
folytonos, véges | II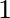 |
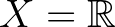 , , |
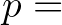 Lebesgue-mérték Lebesgue-mérték 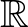 -en -en |
folytonos, végtelen | II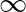 |
Létezik még egy ötödik fajta Neumann-algebra is, a III típus, ez utóbbi egészen különleges, olyannyira, hogy az osztályozás publikálásakor nem is volt ismert példa ilyen Neumann-algebrára. Neumannak csak 1940-ben sikerült az első III típusú faktort megkonstruálnia [42]. Az I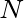 és I
és I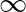 típusok a kvantummechanika Hilbert-tér formalizmusát adják: Az ilyen típusú Neumann-algebrák
típusok a kvantummechanika Hilbert-tér formalizmusát adják: Az ilyen típusú Neumann-algebrák 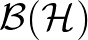 alakúak, ahol
alakúak, ahol 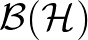 a
a 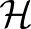 Hilbert-téren értelmezett összes operátorok algebrája. Az ilyen algebrák projektorainak hálója azonos a Hilbert-hálóval. A II
Hilbert-téren értelmezett összes operátorok algebrája. Az ilyen algebrák projektorainak hálója azonos a Hilbert-hálóval. A II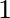 és II
és II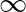 típusok teljesen újnak számítottak 1935-ben. A nem I
típusok teljesen újnak számítottak 1935-ben. A nem I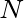 vagy I
vagy I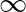 típusú
típusú 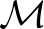 Neumann-algebrák projekcióinak
Neumann-algebrák projekcióinak 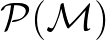 hálói egy normális
hálói egy normális 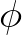 állapottal olyan
állapottal olyan 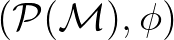 kvantumvalószínűségi tereket alkotnak, amelyek strukturálisan lényegesen különböznek a Hilbert-tér formalizmus valószínűségi terétől: pl. nem atomosak (nincs bennük legkisebb, nem nulla valószínűségű elem). Mint ahogy a klasszikus valószínűségszámításban is előfordulhat, hogy bizonyos jelenségek leírásához szükség van nem diszkrét valószínűségi mértékterekre, bizonyos kvantumfizikai rendszerek sem írhatók le I
kvantumvalószínűségi tereket alkotnak, amelyek strukturálisan lényegesen különböznek a Hilbert-tér formalizmus valószínűségi terétől: pl. nem atomosak (nincs bennük legkisebb, nem nulla valószínűségű elem). Mint ahogy a klasszikus valószínűségszámításban is előfordulhat, hogy bizonyos jelenségek leírásához szükség van nem diszkrét valószínűségi mértékterekre, bizonyos kvantumfizikai rendszerek sem írhatók le I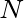 vagy I
vagy I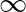 típusú algebrák definiálta kvantumvalószínűségi mértékterekkel – azaz a Hilbert-tér formalizmuson belül. Tipikus ilyen rendszerek a kvantumterek [8] és a kvantumstatisztikus mechanikai rendszerek termodinamikai limeszben [4], [5]. Neumann munkássága az operátoralgebrák területén az 1930-as évek második felében tehát megalkotta azokat a matematikai eszközöket, amelyek a kvantumelmélet e későbbi fejleményei számára kulcsfontosságúnak bizonyultak [15].
típusú algebrák definiálta kvantumvalószínűségi mértékterekkel – azaz a Hilbert-tér formalizmuson belül. Tipikus ilyen rendszerek a kvantumterek [8] és a kvantumstatisztikus mechanikai rendszerek termodinamikai limeszben [4], [5]. Neumann munkássága az operátoralgebrák területén az 1930-as évek második felében tehát megalkotta azokat a matematikai eszközöket, amelyek a kvantumelmélet e későbbi fejleményei számára kulcsfontosságúnak bizonyultak [15].
Neumann ezeket az évtizedekkel későbbi feljeményeket természetesen nem láthatta. Ő úgy gondolta (nagyjából 1935-től), hogy a II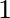 típusú Neumann-algebrák a kvantummechnika számára megfelelőbb matematikai keret, mint az I
típusú Neumann-algebrák a kvantummechnika számára megfelelőbb matematikai keret, mint az I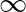 Neumann-algebrák, azaz a Hilbert-tér formalizmus:
Neumann-algebrák, azaz a Hilbert-tér formalizmus:
„… erősen hajlok arra, hogy a Hilbert-téren értelmezett összes korlátos operátorok gyűrűjét (a jelölésünkben a Ieset) kevéssé vegyem komolyan, és a II
esetet komolyabban vegyem, amikor a kvantummechanika végső alapjairól gondolkodom.” [48]
Egyebek mellett amiatt gondolta Neumann így, mert úgy látta, hogy a II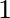 nyújtotta keretben nincsenek jelen bizonyos matematikai patológiák, amelyeket a Hilbert-tér fomalizmusban látott. Ilyen patológia, hogy egy Hilbert-téren értelmezett összes nem korlátos önadjungált operátorok halmazában az algebrai műveletek nem végezhetők el korlátlanul, míg az összes olyan nem korlátos önadjungált operátor, amelynek spektrálprojektorai egy II
nyújtotta keretben nincsenek jelen bizonyos matematikai patológiák, amelyeket a Hilbert-tér fomalizmusban látott. Ilyen patológia, hogy egy Hilbert-téren értelmezett összes nem korlátos önadjungált operátorok halmazában az algebrai műveletek nem végezhetők el korlátlanul, míg az összes olyan nem korlátos önadjungált operátor, amelynek spektrálprojektorai egy II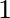 algebrába tartoznak, jól viselkedik algebrailag. Továbbá a
algebrába tartoznak, jól viselkedik algebrailag. Továbbá a 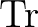 nyom-funkcionál nem korlátos az I
nyom-funkcionál nem korlátos az I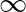 esetben, míg egy II
esetben, míg egy II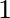 típusú Neumann-algebrán létezik véges nyom
típusú Neumann-algebrán létezik véges nyom 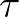 (nyomszerű állapot). Ennek az a jelentősége, hogy az (1) formulában
(nyomszerű állapot). Ennek az a jelentősége, hogy az (1) formulában 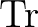 nem értelmezhető valószínűségként a valószínűség Mises-féle értelemben vett [34], [35] relatív gyakorisági interpretációja mellett, mert egy statisztikus sokaságon vett relatív gyakoriságok 1-nél kisebbek. Ez azért volt probléma Neumann számára, mert a [36], [38], [37] dolgozatokban (és a [41] könyvben is) Neumann az (1) formula által adott valószínűséget olyan feltételes valószínűségként értelmezte, amely a
nem értelmezhető valószínűségként a valószínűség Mises-féle értelemben vett [34], [35] relatív gyakorisági interpretációja mellett, mert egy statisztikus sokaságon vett relatív gyakoriságok 1-nél kisebbek. Ez azért volt probléma Neumann számára, mert a [36], [38], [37] dolgozatokban (és a [41] könyvben is) Neumann az (1) formula által adott valószínűséget olyan feltételes valószínűségként értelmezte, amely a 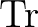 a priori mérték kondícionálásának eredményeképp adódik, és Neumann a valószínűséget Mises szellemében relatív gyakoriságként fogta fel.
a priori mérték kondícionálásának eredményeképp adódik, és Neumann a valószínűséget Mises szellemében relatív gyakoriságként fogta fel.
Ezt az ellenmondást Neumann úgy oldja meg, hogy a 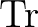 -rel adott valószínűségeket relatív valószínűségekként értelmezi, nem pedig abszolút valószínűségekként. A relatív valószínűség tartalmát nem fejti ki szisztematikusan általában, hanem a következő példán világítja meg [38], [41][310 old.]: Képzeljünk el egy olyan mennyiséget, amely bármely valós értéket egyenlő valószínűséggel vesz fel. Ekkor annak valószínűsége, hogy ezen mennyiség értéke egy véges intervallumba esik, nulla kell legyen, ha megköveteljük a valószínűségi mértéktől, hogy 1-re normált legyen. De ha ezt tesszük, nem kapunk információt arról, mi a viszonya annak a két valószínűségnek, hogy a mennyiség két különböző intervallumba esik. Ez utóbbi információ azonban fontos lehet, és ezt az információt a két intervallum hosszának viszonyát is tartalmazó nem korlátos hosszmérték tartalmazza.
-rel adott valószínűségeket relatív valószínűségekként értelmezi, nem pedig abszolút valószínűségekként. A relatív valószínűség tartalmát nem fejti ki szisztematikusan általában, hanem a következő példán világítja meg [38], [41][310 old.]: Képzeljünk el egy olyan mennyiséget, amely bármely valós értéket egyenlő valószínűséggel vesz fel. Ekkor annak valószínűsége, hogy ezen mennyiség értéke egy véges intervallumba esik, nulla kell legyen, ha megköveteljük a valószínűségi mértéktől, hogy 1-re normált legyen. De ha ezt tesszük, nem kapunk információt arról, mi a viszonya annak a két valószínűségnek, hogy a mennyiség két különböző intervallumba esik. Ez utóbbi információ azonban fontos lehet, és ezt az információt a két intervallum hosszának viszonyát is tartalmazó nem korlátos hosszmérték tartalmazza.
Hogy ezzel a megoldással Neumann nem volt teljesen elégedett, azt egyrészt éppen az mutatja, hogy a II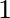 típusú Neumann-algebrák definiálta nemkommutatív valószínűségszámítást alkalmasabbnak találta, mint a Hilbert-tér formalizmust, mert előbbiben létezik egy elvileg relatív gyakoriságként értelmezhető (apriori) valószínűségeket szolgáltató nyom. Másrészt az 1930-as évek közepétől Neumann feladta a kvantumvalószínűségek relativ gyakorisági értelmezését. Azt a munkát [45], amelyben ez a gondolat van kifejtve, Neumann nem publikálta, az töredékben maradt. A relatív gyakorisági értelmezés helyett Neumann egy – részletesen ki nem fejtett – logikai értelmezést lát alkalmasnak, amiről az 1954-es előadásában [43] ezeket mondja:
típusú Neumann-algebrák definiálta nemkommutatív valószínűségszámítást alkalmasabbnak találta, mint a Hilbert-tér formalizmust, mert előbbiben létezik egy elvileg relatív gyakoriságként értelmezhető (apriori) valószínűségeket szolgáltató nyom. Másrészt az 1930-as évek közepétől Neumann feladta a kvantumvalószínűségek relativ gyakorisági értelmezését. Azt a munkát [45], amelyben ez a gondolat van kifejtve, Neumann nem publikálta, az töredékben maradt. A relatív gyakorisági értelmezés helyett Neumann egy – részletesen ki nem fejtett – logikai értelmezést lát alkalmasnak, amiről az 1954-es előadásában [43] ezeket mondja:
„… azokban a rendszerekben, amelyek a kvantumelmélet logikai háttereként szolgálnak, az igaz, hogy amint a logika szokásos fogalmait rögzítjük valamely izomorf transzformációra nézve, a teljes valószínűségelmélet is rögzítődik. […] Amit állítok, az nem más, mint az, hogy a kvantummechanikában az a priori valószínűség fogalma már a legelején egyértelműen adva van. […] Ez azonban azt jelenti, hogy létezik egy formális mechanizmus, amelyben a logika és a valószínűségelmélet a kezdettől fogva egyszerre jön létre és egyszerre származtatható.” [43]
A fenti idézetbeni gondolat teljesen érthető, ha a II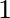 típusú (faktor)
típusú (faktor) 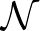 Neumann-algebra által definiált nemkommutatív valószínűségelméletet
Neumann-algebra által definiált nemkommutatív valószínűségelméletet  tekintjük: A
tekintjük: A 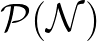 projektorháló a kvantumos analógja a Boole-algebrának mint klasszikus kijelentéslogikának – ez az a struktúra, amit Birkhoff és Neumann kvantumlogikának neveznek híres cikkükben [3], és amely önálló diszciplinává terebélyesedett kutatási területet alapozott meg [7], [23]. Az
projektorháló a kvantumos analógja a Boole-algebrának mint klasszikus kijelentéslogikának – ez az a struktúra, amit Birkhoff és Neumann kvantumlogikának neveznek híres cikkükben [3], és amely önálló diszciplinává terebélyesedett kutatási területet alapozott meg [7], [23]. Az 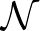 algebra belső automorfizmusai (amiket az
algebra belső automorfizmusai (amiket az 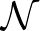 algebra unitér elemei definiálnak), izomorfiznusai a
algebra unitér elemei definiálnak), izomorfiznusai a 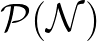 hálónak, és az
hálónak, és az 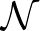 -en a
-en a 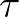 nyom az a korlátos funkcionál, amit egyértelműen meghatároz az a tulajdonság, hogy invariáns az unitér transzformációra.
nyom az a korlátos funkcionál, amit egyértelműen meghatároz az a tulajdonság, hogy invariáns az unitér transzformációra.
Jóllehet 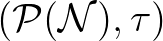 ilymódon kitüntetett nemkommutatív valószínűségelmélet, Neumann gondolata, hogy ez a kvantumelmélet elégséges alapja lehet, fenntarthatatlannak – Araki megfogalmazásában utópiának [1] – bizonyult. Bizonyos kvantumjelenségek leírásához bizonyíthatóan II és III típusú Neumann-algebrákra van szükség (pl. kvantumstatisztikus fizikai rendszerek termodinamikai limeszben való leírásához [4], [5], vagy a relativisztikus kvantumtér-elméletben [8]). A kanonikus (Heisenberg-féle) felcserélési reláció sem reprezentálható egy II
ilymódon kitüntetett nemkommutatív valószínűségelmélet, Neumann gondolata, hogy ez a kvantumelmélet elégséges alapja lehet, fenntarthatatlannak – Araki megfogalmazásában utópiának [1] – bizonyult. Bizonyos kvantumjelenségek leírásához bizonyíthatóan II és III típusú Neumann-algebrákra van szükség (pl. kvantumstatisztikus fizikai rendszerek termodinamikai limeszben való leírásához [4], [5], vagy a relativisztikus kvantumtér-elméletben [8]). A kanonikus (Heisenberg-féle) felcserélési reláció sem reprezentálható egy II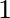 típusú Neumann-algebrán [33] – ellentétben a Hilbert-tér formalizmussal, ahol a felcserélési reláció Schrödinger-reprezentációja nemcsak hogy létezik, de egyértelmű, amint azt épp Neumann bizonyította be [40].
típusú Neumann-algebrán [33] – ellentétben a Hilbert-tér formalizmussal, ahol a felcserélési reláció Schrödinger-reprezentációja nemcsak hogy létezik, de egyértelmű, amint azt épp Neumann bizonyította be [40].
Neumann érdeklődése az 1940-es évektől egyre inkább az alkalmazott matematika és a számítógéptudomány felé fordult, összefüggésben a világtörténelmi eseményekkel. Szisztematikus kutatást a kvantummechanika alapjainak területén sem végzett már ebben az időben, bár intellektuális érdeklódése fennmaradt a terület iránt. Úgy gondolta, hogy a kvantumlogika és a kvantum-valószínűségelmélet egyidejű keletkezése, amire a fentebb idézett 1954-es előadásában utal, axiomatikus kiépítést igényelne, és levelezéséből [46] úgy tűnik, hogy azokban a szabad perceiben, amiket a háborúval (pl. a Los Alamos projekttel) kapcsolatos munkája megengedett, foglalkozott is ezzel a problémával. De ezt a munkát sosem fejezte be. Ezt illető csalódásának így adott kifejezést egy levelében:
„Talán, ha nem szakítanának félbe állandóan utazások és más kötelezettségek, amelyek a még mindig létező háborús munkából fakadnak, képes lettem volna megcsinálni – jóllehet még ebben sem vagyok biztos. Ahogy a dolgok állnak, a munkám minden vonatkozásban kárt szenvedett…” [46]
Az utókor is csak azt mondhatja: kár, hogy nem tudhatjuk, hogyan dolgozta volna ki Neumann ezt a gondolatot. De Neumann eredményei a kvantummechanika matematikai alapjainak területén enélkül is kivételes jelentőségűek.
A Nemzeti Kutatási, Fejlesztési és Innovációs Hivatal támogatásával (K-134275). Köszönet a Hamburg Institute for Advanced Study (HIAS) intézetnek, ahol az írás készült.
Department of Philosophy, Logic and Scientific Method
London School of Economics and Political Science
Irodalomjegyzék
- [1] H. Araki. Some of the legacy of John von Neumann in physics: Theory of measurement, quantum logic and von Neumann algebras in physics. In J. Glimm, J. Impagliazzo, and I. Singer, editors, The Legacy of John von Neumann, volume 50 of Proceedings of Symposia in Pure Mathematics, pages 136–139. American Mathematical Society, Providence, RI, 1990.
[2] F. J. Belinfante. A Survey of Hidden-variable Theories. Pergamon Press, Oxford, 1973.
[3] G. D. Birkhoff and J. von Neumann. The logic of quantum mechanics. Annals of Mathematics, 37:823–843, 1936. Reprinted in [29], No. 7.
[4] O. Bratteli and D. W. Robinson. Operator Algebras and Quantum Statistical Mechanics, volume I. 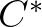 -algebras and von Neumann algebras. Springer Verlag, Berlin, Heidelberg and New York, 1979.
-algebras and von Neumann algebras. Springer Verlag, Berlin, Heidelberg and New York, 1979.
[5] O. Bratteli and D. W. Robinson. Operator Algebras and Quantum Statistical Mechanics, volume II. Equilibrium States, Models in Quantum Statistical Mechanics. Springer Verlag, Berlin, Heidelberg and New York, 1981.
[6] F. Csaba and M. Rédei. „Az intuicionizmus immár semmilyen alapon nem utasítható el” Neumann János Gödel nemteljességi tételeiről és a matematika természetéről. Matematikai Lapok, 11:16–25, 2006.
[7] M. L. Dalla-Chiara, R. Giuntini, and M. Rédei. The history of quantum logic. In D. M. Gabbay, editor, Handbook of History of Logic. Kluwer Academic Publishers, Dordrecht, 2007.
[8] R. Haag. Local Quantum Physics: Fields, Particles, Algebras. Springer Verlag, Berlin and New York, 1992.
[9] D. Hilbert. Mathematical problems. Lecture delivered before the International Congress of Mathematicians at Paris in 1900. In F. E. Browder, editor, Mathematical Developments Arising From Hilbert Problems, volume 28 of Proceedings of Symposia in Pure Mathematics, pages 1–34. American Mathematical Society, Providence, R.I., 1983.
[10] D. Hilbert, J. von Neumann, and L. Nordheim. Über die Grundlagen der Quantenmechanik. Mathematische Annalen, 98:1–30, 1928. Received on April 4, 1927. Reprinted in [30] No. 7.
[11] P. Lax. Foreword. In [22], 2005.
[12] F. J. Murray and J. von Neumann. On rings of operators. Annals of Mathematics, 37:116–229, 1936. Reprinted in [31] No. 2.
[13] F. J. Murray and J. von Neumann. On rings of operators, II. American Mathematical Society Transactions, 41:208–248, 1937. Reprinted in [31] No. 3.
[14] F. J. Murray and J. von Neumann. On rings of operators, IV. Annals of Mathematics, 44:716–808, 1943. Reprinted in [31] No. 5.
[15] D. Petz and M. Rédei. John von Neumann and the theory of operator algebras. In F. Brody and T. Vámos, editors, The Neumann Compendium, volume I of World Scientific Series of 20th Century Mathematics, pages 163–181. World Scientific, Singapore, 1995.
[16] M. Rédei. Why John von Neumann did not like the Hilbert space formalism of quantum mechanics (and what he liked instead). Studies in History and Philosophy of Modern Physics, 27:1309–1321, 1996.
[17] M. Rédei. Quantum Logic in Algebraic Approach, volume 91 of Fundamental Theories of Physics. Kluwer Academic Publisher, 1998.
[18] M. Rédei. „Unsolved problems in mathematics” J. von Neumann's address to the International Congress of Mathematicians Amsterdam, September 2–9, 1954. The Mathematical Intelligencer, 21:7–12, 1999.
[19] M. Rédei. Von Neumann's concept of quantum logic and quantum probability. In M. Rédei and M. Stöltzner, editors, John von Neumann and the Foundations of Quantum Physics, Institute Vienna Circle Yearbook, pages 153–172. Kluwer Academic Publishers, Dordrecht, 2001.
[20] M. Rédei. John von Neumann 1903-1957. European Mathematical Society Newsletter, pages 17–20, March 2004.
[21] M. Rédei. John von Neumann on mathematical and axiomatic physics. In P. Budinich G. Boniolo and M. Trobok, editors, The Role of Mathematics in Physical Sciences: Interdisciplinary and Philosophical Aspects, pages 43–54. Springer, Dordrecht, 2005.
[22] M. Rédei, editor. John von Neumann: Selected Letters, volume 27 of History of Mathematics, Rhode Island, 2005. American Mathematical Society and London Mathematical Society.
[23] M. Rédei. The birth of quantum logic. History and Philosophy of Logic, 28:107–122, May 2007.
[24] M. Rédei. Parallels and divergencies: Gödel and von Neumann. Magyar Filozófiai Szemle, 62(4):168–181, 2018.
[25] M. Rédei. On the tension between physics and mathematics. Journal for General Philosophy of Science, 51:411–425, 2020. open access: https://link.springer.com/article/10.1007/s10838-019-09496-0.
[26] M. Rédei and M. Stöltzner, editors. John von Neumann and the foundations of quantum physics. Institute Vienna Circle Yearbook. Kluwer Academic Publishers, Dordrecht, 2001.
[27] M. Rédei and M. Stöltzner. Soft axiomatization: John von Neumann on method and von Neumann's method in the physical sciences. In E. Carson and R. Huber, editors, Intuition and the Axiomatic Method, volume 70 of Western Ontario Series in Philosophy of Science, pages 235–249. Springer, Dordrecht, 2006.
[28] M. Rédei and S. J. Summers. Quantum probability theory. Studies in History and Philosophy of Modern Physics, 38:390–417, 2007.
[29] A. H. Taub, editor. John von Neumann: Collected Works, volume IV. Continuous Geometry and Other Topics, New York and Oxford, 1961. Pergamon Press.
[30] A. H. Taub, editor. John von Neumann: Collected Works, volume I. Logic, Theory of Sets and Quantum Mechanics, New York and Oxford, 1961. Pergamon Press.
[31] A. H. Taub, editor. John von Neumann: Collected Works, volume III. Rings of Operators, New York and Oxford, 1961. Pergamon Press.
[32] A. H. Taub, editor. John von Neumann: Collected Works, volume II. Operators, Ergodic Theory and Almost Periodic Functions in a Group, New York and Oxford, 1961. Pergamon Press.
[33] G. Valente. John von Neumann's mathematical „Utopia” in quantum theory. Studies in History and Philosophy of Modern Physics, 39:860–871, 2008.
[34] R. von Mises. Grundlagen der Wahrscheinlichkeitsrechnung. Mathematische Zeitschrift, 5:52–99, 1919.
[35] R. von Mises. Probability, Statistics and Truth. Dover Publications, New York, 2nd edition, 1981. Originally published as „Wahrscheinlichkeit, Statistik und Wahrheit” (Springer, 1928).
[36] J. von Neumann. Mathematische Begründung der Quantenmechanik. Göttinger Nachrichten, pages 1–57, 1927. Communicated by M. Born on May 20, 1927. Reprinted in [30] No. 9.
[37] J. von Neumann. Thermodynamik quantenmechanischer Gesamtheiten. Göttinger Nachrichten, pages 273–291, 1927. Communicated by M. Born on November 11, 1927. Reprinted in [30] No. 11.
[38] J. von Neumann. Wahrscheinlichkeitstheoretischer Aufbau der Quantenmechanik. Göttinger Nachrichten, pages 245–272, 1927. Communicated by M. Born on November 11, 1927. Reprinted in [30] No. 10.
[39] J. von Neumann. Allgemeine Eigenwerttheorie Hermitescher Funktionaloperatoren. Mathematische Annalen, 102:49–131, 1930. Received by the journal on December 15, 1928. Reprinted in [32] No. 1.
[40] J. von Neumann. Die Eindeutigkeit der Schrödingerschen operatoren. Mathematische Annalen, 104:570–578, 1931. Reprinted in [32] No. 7.
[41] J. von Neumann. Mathematische Grundlagen der Quantenmechanik. Springer Verlag, Berlin, 1932. English translation: Mathematical Foundations of Quantum Mechanics (Princeton University Press, Princeton) 1955.
[42] J. von Neumann. On rings of operators, III. Annals of Mathematics, 41:94–161, 1940. Reprinted in [31] No. 4.
[43] J. von Neumann. „Unsolved problems in mathematics” J. von Neumann's address to the International Congress of Mathematicians, Amsterdam, September 2–9, 1954. in [26], 1954.
[44] J. von Neumann. The Mathematician. In A. H. Taub, editor, John von Neumann: Collected Works, volume I, pages 1–9. Pergamon Press, New York and Oxford, 1961. Originally published in Works of the Mind Vol. I no. 1 (University of Chicago Press, Chicago, 1947), 180–196.
[45] J. von Neumann. Quantum logic (strict- and probability logics). In A. H. Taub, editor, John von Neumann: Collected Works, volume IV. Continuous Geometry and Other Topics, pages 195–197. Pergamon Press, New York and Oxford, 1961. Unfinished manuscript, reviewed by A. H. Taub.
[46] J. von Neumann. Letter to F. B. Silsbee, July 2, 1945. In M. Rédei, editor, John von Neumann: Selected Letters, volume 27 of History of Mathematics, pages 218–220. American Mathematical Society and London Mathematical Society, Rhode Island, 2005. Original in: von Neumann Papers, Library of Congress.
[47] J. von Neumann. Letter to G. Birkhoff, November 13, 1935 (?). In M. Rédei, editor, John von Neumann: Selected Letters, volume 27 of History of Mathematics, pages 59–64. American Mathematical Society and London Mathematical Society, Rhode Island, 2005. Original in: Papers of G. Birkhoff, Harvard University Archives, Accession 13493.
[48] J. von Neumann. Letter to G. Birkhoff, November 6, 1935 (?). In M. Rédei, editor, John von Neumann: Selected Letters, volume 27 of History of Mathematics, pages 52–58. American Mathematical Society and London Mathematical Society, Rhode Island, 2005. Original in: Papers of G. Birkhoff, Harvard University Archives, Accession 13493.
[49] A. S. Wightman. Hilbert's 6th problem. In F. E. Browder, editor, Mathematical Developments Arising from Hilbert Problems, volume 28 of Proceedings of Symposia in Pure Mathematics, pages 147–240. American Mathematical Society, Providence, R.I., 1983.











