T. Sós Vera

Amikor legutóbb T. Sós Verát 90. születésnapján köszönthettem, azzal kellett kezdenem, hogy Verát 1962-ben, érettségizőként ismertem meg, amikor az olimpiai szakkör vezetője, Reiman István (nagyon kedves tanárunk) elhívta őt, hogy tartson előadást nekünk. ¹

Én mindig nagyon örültem annak, hogy a környezetemben nagyon sok kiemelkedő személyiség volt, kiemelkedően okosak, kiemelkedően tehetségesek, és még sok más szempontból is kiválóak. Amikor rájuk emlékezünk, akkor mindig vigyáznunk kell arra, hogy személyesek legyünk, de róla beszéljünk, írjunk, ne saját magunkról.

Veráról beszélve legalább négy dolgot kell kiemelnünk: kiváló matematikus, kiváló egyetemi oktató, kiváló és nagyon-nagyon megnyerő ember volt. Amikor elsőéves hallgató lettem, heti 9 analízis és 2 kombinatorika órát tartott matematika szakos évfolyamunknak. Amit ott tanultunk, azért csak hálásak lehettünk: hihetetlenül sokat tanultunk tőle. Évfolyamunknak és még jó néhány évfolyamnak a legkedveltebb oktatója volt. (Lehet, hogy ma már mulatságosnak tűnik, de szavaztunk erről, és egyértelműen Vera nyert.) Kiemelendő az is, hogy nem csak jól választotta meg a tananyagot, de mert, merészelt nehéz anyagot is választani. Amikor elsőéves analízist oktatott, levezette a láncgörbe alakját, azaz, implicite megoldotta nekünk a megfelelő differenciálegyenletet. Sokszor egészen új matematikai területeket Vera vezetett be a magyar matematikába. Abban is döntő szerepe volt, hogy mi került bele a tananyagunkba diszkrét matematikából.

Itt némi magyarázattal is tartozom. A háború után az egyetemi rendszer a világ nagyon sok országában, így Magyarországon is döntően megváltozott. Nagyon megnőtt például az egyetemre felvettek száma.²  Később, 1956 után egy második átalakulás is megfigyelhető volt: a tanári szakok mellett megjelentek a kutató szakok is. Ez azt is jelentette, hogy míg korábban matematika-fizika tanárokat képeztek, akik oktatásuk közepén szakosodtak tanároknak, vagy matematikusoknak, vagy fizikusoknak, 1957-ben beindították a fizikusképzést. Ez azt jelentette, hogy az érettségi után rögtön fizikusoknak vették fel a diákok egy részét. 1961-ben beindították a matematikusképzést³, illetve például 1963-ban a biológusképzést is (korábban induláskor csak a megfelelő tanárképzés létezett). Számunkra ez két szempontból is fontos volt. Vera tanította például az induló fizikus szakot, később minket, matematikus szakosokat is, és sok évig a tanár szakos hallgatókat is, pl. analízisre. Az új képzések kialakulásakor a matematikusoknál sok idő szabadult fel azáltal, hogy szinte alig tanultunk fizikát, (ennek voltak előnyei és hátrányai is). Ezért néhány oktatónak át kellett gondolni, milyen új tantárgyakat kellene bevezetni, hogy egy modern matematikusi képzést kapjunk. Vera már diákkora óta részt vett a legkülönbözőbb tantárgyak oktatásában, és az új tanmenet kialakításban nagyon komoly szerepe volt.

Ezek az átalakítások néha komoly vitákban alakultak ki, amiben sajnos néha nemcsak szakmai szempontoknak volt szerepük, hanem annak is, hogy a sok órát tartó tanszékeknek több lehetőségük volt oktatók felvételére.

Az eredetileg kialakított rendszer egyébként akkor változott meg, amikor Berkes, Laczkovich, Lovász, Pósa, Pelikán évfolyama harmadéves lett. Ekkor alakult ki, hogy a harmadévesek a matematikán belül is szakosodtak.

A korábbi matematikatanári oktatásban szinte semmi kombinatorika nem szerepelt, talán Vera, Hajnal András és Rényi hatására alakult ki a modern diszkrét matematikai (kombinatorikai-gráfelméleti) oktatás. Ebben volt kiemelkedő szerepe Verának. Bevezette a gráfelmélet oktatását, majd ezen belül algoritmusokat is tanított, és például amikor a világ matematikájában megjelentek a matroidok, amelyekről leegyszerűsítve azt mondhatnánk, hogy a mátrixokat és a gráfokat általánosította, akkor Vera rögtön speciális előadást, pontosabban szemináriumot indított ebből a témából is.

Amikor a mi évfolyamunknál befejezte a kombinatorika félévet, akkor Vera azt tovább folytatta egy gráfelméleti speciálelőadással, és mivel minden matematikus imádta előadási stílusát, a szemináriumán a legkülönbözőbb évfolyamok hallgatói töltötték meg a termet. Itt született meg a Katona-Nemetz-Simonovits cikkünk is (Katona és Nemetz három évvel feljebb jártak, mint én). Ez Nemetz Tibinek és nekem az első cikkem volt, és ma is sok nemzetközi hivatkozás születik rá, bár a cikk csak magyarul jelent meg. Ugyancsak ezen a speciálelőadáson adta elő azt az Erdős-cikket, amely egyik sejtésének megoldása volt Lovász Lacival két fontosabb közös cikkünk alapja.

De azt gondolom, Vera hatására született meg a Gyárfás-Gerencsér cikk is, amelyik nagy változást jelentett az általánosított Ramsey-elméletben is, illetve Kéri Gerzson cikke, amelyikben a Ramsey-küszöb egy javítását adta. (Emellett persze más hatásokat is említhetnék a környezetben, elsősorban Erdős, Gallai, Hajnal és Rényi hatását.)

De Vera nemcsak a véges matematikában, hanem más területeken is úttörő volt. Itt csak két apróbb dolgot említenék meg. Amikor a Berkes-Laczkovich-Lovász-Pelikán-Pósa évfolyam befejezte az első félévet, Vera úgy vélte, érdemes számukra egy külön speciálelőadást tartani a valós számok felépítéséről, axiómáiról. Ugyanezt a kérdést Hajós „.A geometria alapjai"-ban csak sokkal később tárgyalta (a Hilbert-féle felépítést követve).

Minden egyéb mellett ki kell emelnem Vera emberi tulajdonságait, a hihetetlen kedves, megnyerő egyéniségét, emberismeretét és az empátiáját is. És azt, hogy mindig nagyon törődött a környezetében levő fiatalokkal, és általában az emberekkel.

Verát 90. születésnapján a Rényi Intézetben öten köszöntöttük fel. Ha reális képet szerettünk volna adni Vera mérhetetlenül sok jó tulajdonságáról, akkor sokkal több előadó és idő kellett volna erre. (Ezt más fórumokon meg is tettük és meg is fogjuk tenni.) Amikor Vera végighallgatta azt a sok jót, amit róla ott elmondtunk, akkor szerényen csak annyit mondott, örülne, ha ennek a fele igaz lenne. (Ebben persze nem volt igaza, az a sok jó mind igaz volt.)

Mi, akik sok éve ismertük Verát, sokan vagyunk, akik először tanítványai voltunk, munkatársai, majd lassanként barátaivá váltunk. Úgy érezzük, hogy nagyon szerencsések voltunk ezzel. Én magam az egyetem elvégzése után három munkahely közül választhattam, és azt választottam, hogy Verával egy tanszéken, a Császár Ákos vezette Analízis I tanszéken dolgozzam. Ugyanezen az egyébként pici tanszéken dolgozott Hajnal András is, Rényi Kató is, Juhász Pista, majd később Pósa Lajos, Laczkovich Miki, Elekes Gyuri, és még sok kiemelkedő matematikus. (Formailag nem, de valójában ugyanitt dolgozott Péter Rózsa is, illetve később Lempert Laci, majd Szűcs Andris is, sőt formailag egy rövid ideig Lovász Laci is.)

Tömören, de kicsit alaposabban azt kellene elmondanom, hogy

Vera legendás tanárunk volt, nekünk, és még sok más fizikus, matematikus, és matematika-fizika tanári évfolyamoknak minden kétségen felül az egyik legnagyobb hatású tanárunk. Gyakran még ma is érezzük hatását a gondolkodásunkban, matematizálásunkban, vagy amikor tanítunk, akkor abban is, hogy hogyan adunk elő. Három ember volt döntő hatással rám a matematikussá válásomban, Vera, Erdős, és Turán. Mindhármuktól nagyon sokat kaptam.

Vera nemzetközi hírű, kiemelkedő matematikus volt. Eredményeivel, sejtéseivel, kérdéseivel számtalan területen indított el újabb kutatásokat. Bizonyos kérdései, illetve tételei körül egész elméletek alakultak ki, ezekre vonatkozóan naponta jelennek meg újabb és újabb eredmények kitűnő matematikusoktól.

Fejér Lipótnál doktorált, majd kezdetben az 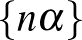sorozatok eloszlásának egyenletességéről bizonyított be fontos tételeket. Idevonatkozó eredményei erősen hatottak a diszkrepancia-elméletben, egyebek között a Hlawka körül kialakult bécsi iskolára. Nagy számelméleti hatása mellett a kombinatorikai hatása is nagyon nagy volt. Erdős mellett talán Vera egyike azoknak, akinek a magyar kombinatorika sikerességében a legkiemelkedőbb szerepe volt.

Vera a matematikát legalább három okból szerette. Megszerette, mert kitűnő volt a gimnáziumi matematikatanára, Gallai Tibor. Szerette a matematikát a szépsége miatt, szerette, mert valamilyen értelemben biztonságot is adott neki, és szerette, mert élete nehezebb periódusaiban extra biztonságot is nyújtott neki.

Bal szélen Gallai Tibor beszélget Sós Verával (1958)

Vera matematikáját az is jellemezte, hogy kitűnő kérdéseket tudott feltenni. Ezek közül nem egy vált a diszkrét matematika egy alterületének elindítójává. Sokszor vitatkoztunk olyasmin, hogy egy adott területen érdekes kérdést mikor érdemes egészen más területekre is kiterjeszteni. Itt a következőket említeném meg.

(a) Ha eltekintek attól, hogy Erdős problémafelvető cikkei gyakran számítottak survey (azaz összefoglaló) cikkeknek, akkor az első összefoglaló cikket Sós Verától olvastam: az 1976-os római cikkében Vera a véges geometriák, a gráfelmélet, illetve a metszettételek kapcsolatát vizsgálta. Sok fontos survey cikket írt, a survey cikkek írását is tőle tanultam, sőt írtunk közös survey cikkeket is. Ezek közül a Ramsey–Turán survey cikkünket emelném ki.

(b) A kombinatorikus számelméletben fontosak a Sidon-sorozatok. Babai Laci és Sós Vera kiterjesztették ezeket Abel-csoportokra is, és azóta nagyon sok olyan eredmény jelent meg, amelyekben különböző kombinatorikus számelméleti kérdések vannak kiterjesztve Abel-csoportokra, vagy tetszőleges csoportokra. Fried Ervinnel a híres 3-távolság tételét terjesztette ki algebrai struktúrákra.

Vera mint tudományszervező is a legnagyobb hatásúak közé tartozik. A Magyarországon megszervezett kombinatorikai konferenciákkal is nagyon nagy lépést tett abba az irányba, hogy a magyar matematika nemzetközileg ennyire elismert legyen. Amikor konferenciákat szervezett, természetesen a legfontosabb az volt számára, hogy magas színvonalú konferenciát szervezzen, de emellett a fontos szervezési kérdésekre, illetve apróságokra is nagyon odafigyelt.

A magas szinthez az is hozzájárult, hogy a magyar kombinatorikai-gráfelméleti konferenciák találkozóhelyek voltak a nyugati és a szocialista országok legjobb matematikusai között. Az első nagyobb ilyen konferencia a tihanyi volt (főszervezői Erdős és Katona voltak, de Vera munkája is nagyon meglátszott rajta.) Ezek után sorra jöttek a további nemzetközi magyarországi kombinatorikai konferenciák, amelyek szintje többnyire akkoriban messze meghaladta a többi kombinatorikai konferencia szintjét.

Mind szakmai, mind tudományszervező elismertségét nagyon jól tükrözi az, hogy mennyire sok nemzetközi folyóirat szerkesztőbizottsági tagja, hogy nemzetközi konferenciák rendszeres meghívottja volt, és még sok hasonló adat.

Vera nagyon odafigyelt a környezetére, nagyon törődött az emberekkel, tanácsai gyakran meghatározó hatással voltak a környezetében élőkre is.  (Amikor Szűcs Andris sok éve dolgozott átmeneti állásban, akkor is Vera volt, aki úgy döntött, ezt már nem lehet így folytatni, és véglegesítette őt a tanszékén.) Szociális érzékenységére az is jellemző, hogy kiemelten figyelt a környezetében levő személyek mellett például arra is, hogy mi történik a tanárokkal. 

Az alábbiakban írnék néhány szót Sós Vera matematikájáról is, bár itt a mélyebb, nehezen érthető részeket elkerülöm. Az egyik cikkéből nőtt ki a Ramsey–Turán-elmélet, ahol olyan kérdésekről van szó, hogy ha például egy 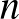csúcsú gráfban nincs 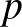pontú teljes részgráf és nincs sok független pont, akkor legfeljebb hány éle lehet. Az idevonatkozó Erdős–Sós-cikkek, illetve a Brown–Erdős–Sós-kérdések is a kombinatorika újabb területét indították el. Híres Erdős–Rényi–Sós-tétel a barátság-tétel, mely szerint ha egy társaságban bármely két embernek pontosan egy közös barátja van, az csak úgy lehet, ha a barátsági gráf nagyon speciális: van egy ember, akinek mindenki a barátja.

Erdős Pállal

A számelméleti és egyéb eredményei is gyakran ahhoz kapcsolódnak, melyek azok a struktúrák, amelyek nem véletlen struktúrák, de úgy viselkednek, mintha véletlen struktúrák lennének. Ilyen struktúrák az 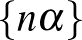 sorozatok is, ezek egyenletes eloszlásúak, fontosak pl. a numerikus integrálásban is, de emellett a modern számítógéptudományban a véletlen számsorozatokat is helyettesítik, ezért váltak fontossá azon területeken, ahol a véletlen bitek felhasználása sokat gyorsít az algoritmusokon. Donald E. Knuth háromkötetes könyve (magyarul is megjelent) az elméleti számítógéptudomány „bibliájának” számított. Ennek nagyon nagy része foglalkozik ezzel a kérdéssel, és meglepetésünkre hivatkozott Vera ún. 3-távolság tételére. Amikor Sós Vera hatásáról beszélünk, én most mégis egy látszólagos apróságot emelnék ki. Amikor diák voltam, nagyon sokat kaptam Vera előadásainak hallgatásából, és abból is, ahogy a diákkörért felelős tanárok egyikeként, mennyire profi módon és áldozatosan végezte ezt a munkáját is. (Hosszú ideig Hajnal András és Sós Vera felügyelte a diákkört, ami a legtehetségesebb diákok szempontjából nagyon fontos volt.) Ezt, vagyis hogy hogyan kell úgy előadni, hogy az az átlagos hallgatóknak is jó legyen, de a legtehetségesebbeknek is, többen tanultuk meg tőle. Én magam biztosan, de nekem úgy tűnik, hogy Katona Gyuszi, Lovász Laci, Elekes Gyuri, vagy Babai Laci is, és még sokan mások is sok mindent Verától tanultunk.

Elöl ülnek Füredi Zoltán, Katona Gyula és T. Sós Vera

Lovász Laci Vera egyik születésnapi üdvözlését, az Érintőben írt cikkét így fejezte be:

Köszönöm a tanítást, támogatást, segítséget, közös munkát, és remélem és kívánom, hogy még sokáig kaphatok bölcs tanácsot, mély lényeglátást T. Sós Verától.

Amikor Vera meghalt, az évfolyamomnak is megírtam ezt, meglepődtem, hogy a levelemre sokan válaszoltak. Bellay Ági, aki a Műegyetemen volt oktató, azt írta:

Én is az Analizist tanultam Verátol, de a szeretetet, tiszteletet, a pedagógiát is. Köszönöm neki! Sajnálom, hogy időben nem köszöntem meg. Igen, jegyzeteim, segédleteim alapját a Verától tanultak képezték.

Kéri Gerzson csak ennyit írt:

Úgy vélem, a legjobb tanár volt azok közül aki tanította az évfolyamunkat. Nyugodjék békében.

Fritz Jóska, aki fizikusnak kezdett, egy évvel felettünk, de azután évvesztéssel átjött hozzánk matematikusnak, elmondta, hogy ebben nagyon befolyásolták Vera előadásai is. (Ehhez tartozik, hogy sokszor Vera által tanított fizikusok is átjöttek hozzánk, Vera analízis előadására.)

… és még folytathatnám.

Vera tudta a matematikában és a mindennapi életben is, hogy mi a fontos. Emellett mindig kereste a látszólag távoleső területek közötti kapcsolatokat, összefüggéseket. (Egyik fontos elve az volt, hogy „minden mindennel összefügg”.)

Említettem, hogy Vera nagyon törődött az emberekkel. Ha pl. egy fiatalabb matematikus eljutott odáig, hogy már ideje volt megírnia a kandidátusi, vagy a nagydoktori disszertációját, akkor szólt neki, rábeszélte, hogy ne halogassa tovább a megírást. Amikor a környezetében valakinek nem volt megfelelő állása, arra is nagyon odafigyelt.

Emellett számtalan más, nem matematikai terület iránt is érdeklődött, szeretett kirándulni, utazni, zenét hallgatni (koncertre, vagy operába menni. Nagyon harmonikus családban élt. Férje, Turán Pál, a magyar matematika egyik legkiemelkedőbb alakja volt, Erdős Pál egyik legjobb barátja. Két gyereke, György és Tamás szintén matematikusként végeztek, Gyuri matematika professzor Chicagóban, Tamás ma a hebraisztika kiemelkedő kutatója Budapesten és Jeruzsálemben.

Abban a 90-edik születésnapi köszöntőmben még azt is kiemeltem, hogy „Verában egy csalást látok. A személyi igazolványa szerint 90 éves elmúlt, de valójában ennél sokkal fiatalabb, a megjelenésében és a gondolkodásában is. Egyébként is, az utóbbi 40 évben Vera 10-20 évet bármikor letagadhatott volna a korából.”

Amikor Erdős meghalt, Vojta Rödl a következőket írta: „Things won't be the same without uncle Paul.” Nehéz valakit Erdőshöz hasonlítani, valamilyen értelemben most mégis ugyanez mondható Veráról. Már most nagyon hiányzik.

Sós Vera, egyik legkedvesebb barátom, egyike azon embereknek, akik sok szempontból, matematikailag és nem-matematikailag a legnagyobb hatással voltak rám. Amikor 92 évesen elesett és kórházba került, tudtam, hogy életveszélybe került. Mégis megdöbbentem, amikor meghalt. Újra és újra fájón megdöbbenek, amikor valamiért felhívnám, és ráébredek, hogy többé már nem hívhatom fel.

Lábjegyzetek

¹

Az olvasónak kicsit furcsa lehet, hogy ebben a cikkben nemzetközileg nagyon elismert matematikusokról a titulusuk kiírása nélkül írok, keresztnevükön vagy becenevükön említve őket, azokon a neveken, amelyeket a környezetünk használt, de ez a hagyományokban így alakult. Erdős Pál ebben kivétel, hiszen őt sokan E.P.-nek hívták, vagy Palinak, a fiatalabbak Pali bácsinak szólították, illetve Erdősként hivatkoztak rá. Erdős jellemző tulajdonsága volt, hogy amikor leült beszélgetni velünk, úgy beszélt, mintha egyenlő nagyságok lennénk.

Révész Pál, amikor Rényi Alfrédról szólt, elmondta azt is, hogy eleinte furcsa volt neki és a környezetének, hogy professzorukat, a nagy matematikust egyszerűen Bubának szólítsák. 50-60 évvel ezelőtt az is szokatlan volt, hogy a környezetünkben az emberek többsége tegezte egymást (Verával ez 1970 után kezdődött). Sokan tegeződtünk a diákjainkkal is.

Az itt említettek közül Rényi Alfréd tanszékvezető és a ma róla elnevezett Intézet vezetője volt. Akadémikus volt T. Sós Vera, férje, Turán Pál, középiskolai tanára, Gallai Tibor, Hajnal András, Péter Rózsa. Akadémikusok továbbá Babai László, Laczkovich Miklós, Lovász László, Katona Gyula, Szűcs András, Fritz József és Simonovits Miklós is. (Emellett nagyon sok akadémikust vagy a tudományok nagydoktorát említhettem volna, például nem említettem Szemerédi Endrét sem, a kombinatorika és a számelméleti iskola egyik legkiemelkedőbb alakját, csak mert nem írtam bizonyos témákról, és mert Szemerédi elsősorban Turán Pált szokta kiemelni azok közül, akik hatottak rá.)

²

Előfordult, hogy egy évben 80 vegyészmérnököt vettek fel, a következőben már 320-at. A rendszerváltozás elött ez már visszájára fordult, kevesebb hallgatót vettek fel, mint amennyien nyugdíjba mentek.

³

Az első évben csak 14 hallgatót vettek fel, a másodikban már 26-ot, és ahogyan megjelentek a számítógépek és a számítógép-programozás, ez a szám meredeken ment felfelé, de egy idő után beindult nagy létszámmal a programozó-programtervező képzés is.

 Simonovits Miklós