Nagy öröm Sós Verát, oly sokunk munkatársát, akadémiai mamáját vagy nagymamáját, a magyar kombinatorikus iskola nagyasszonyát 90. születésnapján köszönteni. De nehéz feladat is, hiszen olyan sok minden tódul az ember fejébe: fontos és gyönyörű matematikai eredményei; elragadó egyetemi és konferencia-előadásai; új tárgyak bevezetése az oktatásba; személyes törődése munkatársaival és tanítványaival; díjai és elismerései; a tudományos közélet odaadó szolgálata itthon és nemzetközi téren.
Lehetetlen volna mindezekről egy rövid születésnapi köszöntőben olyan részletesen írni, ahogyan kellene. Ehelyett megpróbálom kiemelni három-négy eredményét, és megvilágítani azok hátterét és hatását.
Számelmélet, egyenletes eloszlás
Sós Vera első nagyon jelentős kutatásai a számelmélethez, konkrétan egy 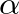 irracionális szám többszörösei törtrészeinek eloszlásához kapcsolódnak.
irracionális szám többszörösei törtrészeinek eloszlásához kapcsolódnak.
A problémakör szokásos szemléltetéseként vegyünk egy egységnyi kerületű kört, és egy adott kiinduló pontból (nevezzük ezt 0-nak) mérjünk fel egy 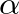 hosszúságú ívet (mondjuk pozitív körüljárási irányban), majd ennek végpontjából egy másik
hosszúságú ívet (mondjuk pozitív körüljárási irányban), majd ennek végpontjából egy másik 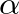 hosszúságú ívet, és ezt ismételjük
hosszúságú ívet, és ezt ismételjük 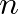 -szer (1. ábra). Kapunk így a körön
-szer (1. ábra). Kapunk így a körön 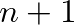 pontot, melyek a kört
pontot, melyek a kört 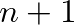 ívre osztják (1. ábra). A
ívre osztják (1. ábra). A 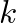 -adik pont távolsága a 0-tól, pozitív irányban,
-adik pont távolsága a 0-tól, pozitív irányban, 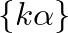 (
(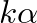 tört része), és ezt a pontot így fogjuk nevezni.
tört része), és ezt a pontot így fogjuk nevezni.
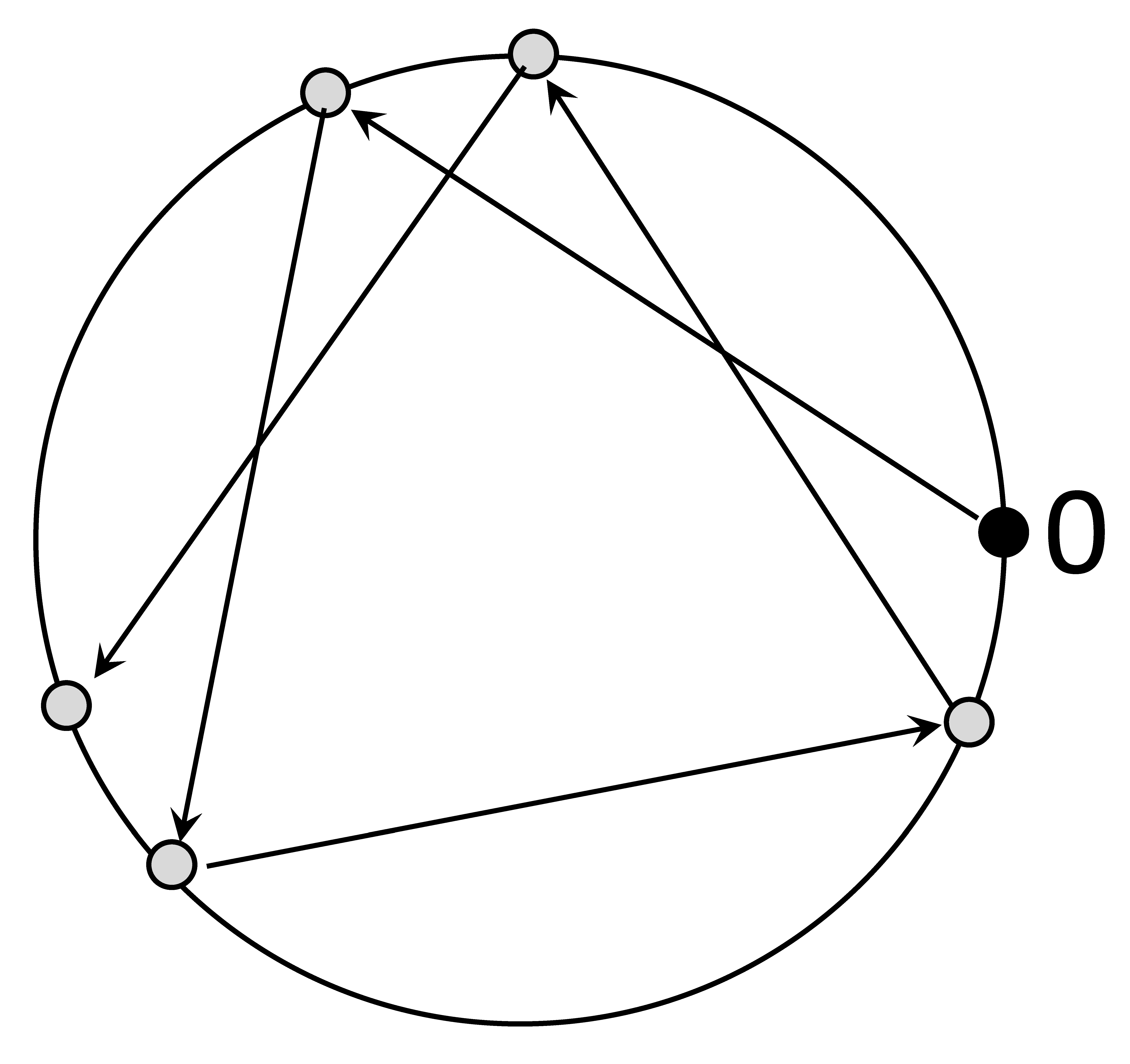
1. ábra. Lépések egy egységnyi kerületű körön.
Ha 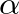 racionális szám, akkor a kapott pontsorozat periodikus lesz (periódusa az
racionális szám, akkor a kapott pontsorozat periodikus lesz (periódusa az 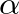 nevezője, mondjuk
nevezője, mondjuk 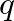 ), és csupa egyforma,
), és csupa egyforma,  hosszúságú ívre osztják a kört. Egészen más a helyzet, ha
hosszúságú ívre osztják a kört. Egészen más a helyzet, ha 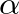 irracionális. Ekkor
irracionális. Ekkor 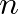 növekedtével egyre kisebb ívek keletkeznek. De így is bizonyítható egy fontos szabályossága ezeknek az ívhosszaknak:
növekedtével egyre kisebb ívek keletkeznek. De így is bizonyítható egy fontos szabályossága ezeknek az ívhosszaknak:
Három-távolság tétel. Bármely 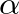 irracionális számra és
irracionális számra és 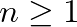 egész számra, a
egész számra, a 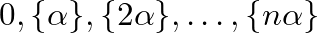 pontok a kört olyan ívekre osztják, melyek között legfeljebb három különböző hosszúságú van. Ha pontosan három van, akkor a legnagyobb ívhossz a másik két ívhossz összege.
pontok a kört olyan ívekre osztják, melyek között legfeljebb három különböző hosszúságú van. Ha pontosan három van, akkor a legnagyobb ívhossz a másik két ívhossz összege.
Ezt a tényt Steinhaus sejtette, és 1958-ban bizonyította be Sós Vera és (tőle függetlenül) Surányi János és Świerczkowski.
Az, hogy a távolságok egyre kisebbek lesznek, azt jelenti, hogy ha 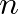 végtelenhez tart, akkor az
végtelenhez tart, akkor az 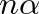 pontok mindenütt sűrűn fognak elhelyezkedni, vagyis minden ívre előbb-utóbb jut belőlük. Ennél azonban sokkal több igaz. Weyl, Sierpiński és Bohl bizonyították be 1910 körül, hogy minden
pontok mindenütt sűrűn fognak elhelyezkedni, vagyis minden ívre előbb-utóbb jut belőlük. Ennél azonban sokkal több igaz. Weyl, Sierpiński és Bohl bizonyították be 1910 körül, hogy minden 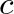 hosszúságú ívre aszimptotikusan
hosszúságú ívre aszimptotikusan 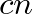 pont jut, vagyis a pontok eloszlása ebben az értelemben egyenletes.
pont jut, vagyis a pontok eloszlása ebben az értelemben egyenletes.
De mekkora hibát („diszkrepanciát”) takar az „aszimptotikusan” kifejezés? Ez már nehéz kérdésekhez vezet, és Sós Vera igen jelentősen járult hozzá a kérdés megválaszolásához. Egyik legjelentősebb eredménye egy diszkrepancia-formula levezetése, amelyből a sorozat eloszlásának szinte minden tulajdonsága leolvasható. (A formula kimondása túlmutat ennek a köszöntőnek a keretein.)
Kiderült (elsősorban Sós Vera kezdeményezésére), hogy nem csak az 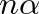 sorozatok, hanem általános számsorozatok eloszlására vonatkozóan is hasonló eredmények bizonyíthatók. Ezek az eredmények fontosak a dinamikus rendszerek modern elméletében és a numerikus integrálásban is.
sorozatok, hanem általános számsorozatok eloszlására vonatkozóan is hasonló eredmények bizonyíthatók. Ezek az eredmények fontosak a dinamikus rendszerek modern elméletében és a numerikus integrálásban is.
Gráfelmélet
Sós Vera másik nagy kutatási területe a gráfelmélet, annak több ága és kérdésköre. Beszéljünk először az extremális gráfelméletről. Ennek keletkezését az 1940-es évektől számítjuk, Turán Pál tételének megjelenésétől. A terület számos kulcsfontosságú problémája és eredménye Erdős Páltól származik, akinek egyik legközvetlenebb, legszorosabban együtt dolgozó munkatársa Sós Vera volt.
Sós Vera egyik nagy erőssége, hogy látszólag távolálló problémák között mély analógiákat, összefüggéseket tud feltárni. Így elsők között volt annak felismerésében és propagálásában, hogy meglepő módon a számelméletben az egyenletes eloszlások elmélete és az extremaális gráfelmélet számos eredménye szorosan összefüggnek egymással.
– Az egyenletes eloszlásra vonatkozó diszkrepancia-tételek azt mondják ki, hogy akárhogyan is veszünk a ![$[0,1]$](/images/stories/latexuj/2020-08/2020-08-lovaszlaszlotsosvera/img15.png) intervallumból egy számsorozatot, lesz olyan
intervallumból egy számsorozatot, lesz olyan 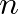 és olyan
és olyan 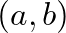 részintervallum, hogy az első
részintervallum, hogy az első 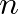 számból lényegesen több vagy kevesebb esik ebbe az intervallumba, mint
számból lényegesen több vagy kevesebb esik ebbe az intervallumba, mint 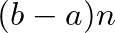 (amennyit várnánk).
(amennyit várnánk).
– A fent említett Turán-tétel azt mondja ki (legegyszerűbb, bár nem legélesebb megfogalmazásban), hogy ha egy 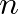 csúcsú gráfban több, mint
csúcsú gráfban több, mint 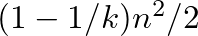 él van, akkor van benne
él van, akkor van benne 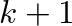 csúcsú teljes gráf; vagyis van olyan
csúcsú teljes gráf; vagyis van olyan 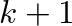 elemű csúcshalmaz, amibe lényegesen több él esik, mint az átlag.
elemű csúcshalmaz, amibe lényegesen több él esik, mint az átlag.
Láthatjuk, hogy mindkét tétel azt mondja ki, hogy bizonyos halmazok nem lehetnek teljesen egyenletesen szétterítve. Hasonló eredmény Ramsey tétele is, és nyilván ez is motiválta Sós Verát, hogy Ramsey és Turán tételeinek közös általánosítását dolgozza ki Erdős Pállal.
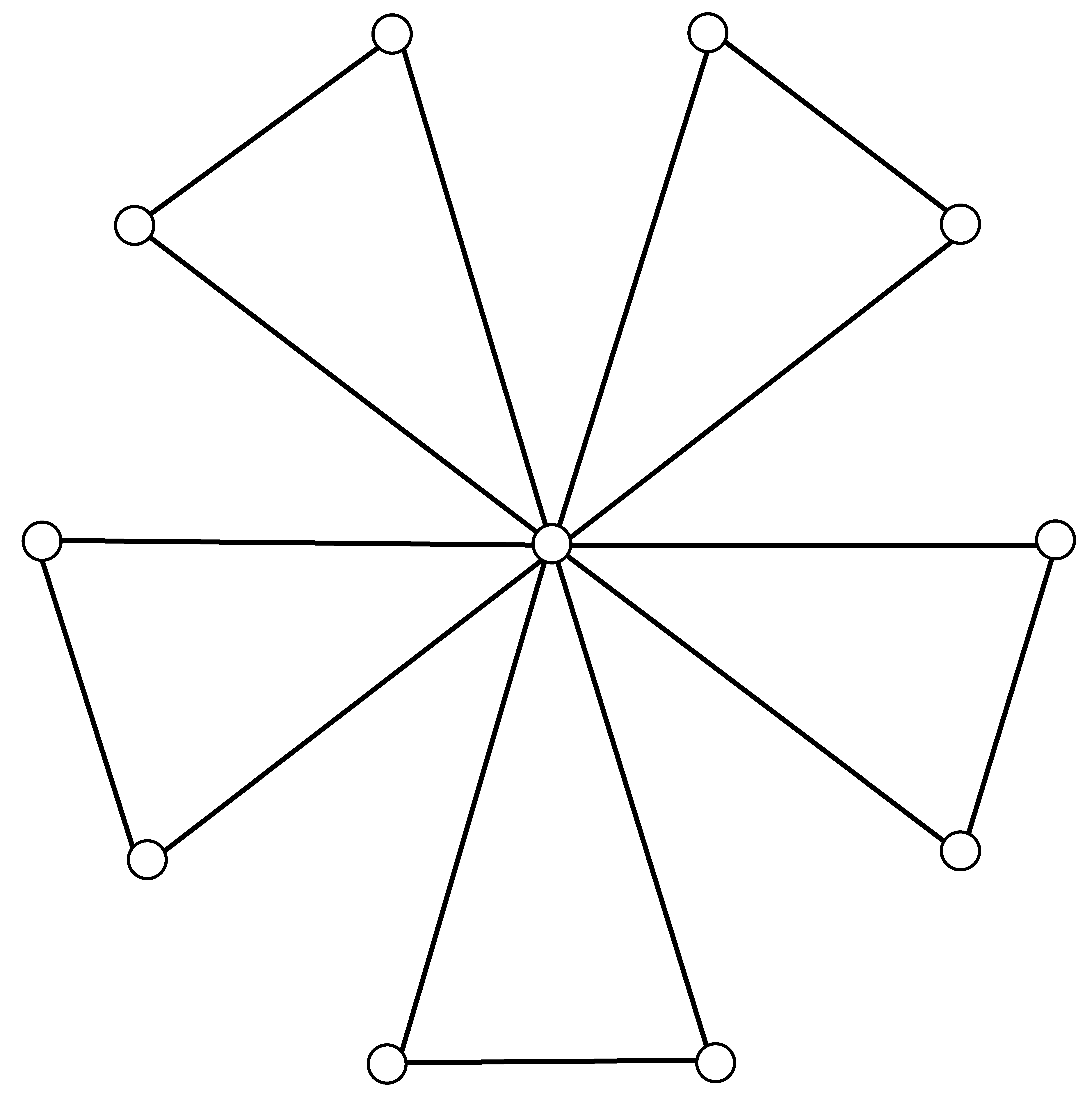
2. ábra. A szélmalom-gráf
Egyszerűen megfogalmazható, de igen sokat idézett gyöngyszem Erdős Pál, Rényi Alfréd és T. Sós Vera „barátság tétele” (Friendship Theorem). Nevezzük szélmalomnak az olyan gráfot, mely olyan háromszögek úniója, melyeknek egyetlen 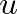 közös pontja van (2. ábra). Könnyű ellenőrizni, hogy egy szélmalomban bármely két csúcsnak pontosan egy közös szomszédja van. A tétel ennek megfordítása:
közös pontja van (2. ábra). Könnyű ellenőrizni, hogy egy szélmalomban bármely két csúcsnak pontosan egy közös szomszédja van. A tétel ennek megfordítása:
Ha egy véges gráfban bármely két csúcsnak pontosan egy közös szomszédja van, akkor az szélmalom.
Ennek a tételnek számos bizonyítását publikálták. Szinte mindegyik azzal a megfigyeléssel indul, hogy ha két csúcs nincs összekötve, akkor a fokuk azonos.
[Ha 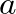 és
és 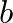 nincs összekötve, akkor
nincs összekötve, akkor 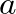 minden
minden 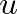 szomszédjához – a feltevés szerint – pontosan egy olyan
szomszédjához – a feltevés szerint – pontosan egy olyan 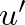 csúcs van a gráfban, mely
csúcs van a gráfban, mely 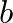 -nek is és
-nek is és 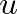 -nak is szomszédja. Könnyű belátni, hogy az
-nak is szomszédja. Könnyű belátni, hogy az 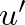 csúcsok mind különbözőek: ha
csúcsok mind különbözőek: ha 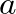 -nak
-nak 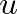 és
és 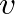 szomszédai, és
szomszédai, és 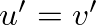 volna, akkor
volna, akkor 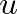 -nak és
-nak és 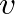 -nek két közös szomszédja volna,
-nek két közös szomszédja volna, 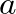 és
és 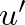 . Így tehát
. Így tehát 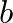 -nek legalább annyi szomszédja van, mint
-nek legalább annyi szomszédja van, mint 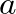 -nak. Felcsrélve
-nak. Felcsrélve 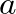 és
és 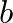 szerepét látjuk, hogy fokuk azonos.]
szerepét látjuk, hogy fokuk azonos.]
Egyszerű feladat innen azt belátni, hogy legfeljebb egy kivétellel minden pont foka azonos. Ha egyetlen kivétel van, akkor az minden más ponttal össze van kötve, és azonnal eljutunk a szélmalomhoz. De mi van, ha minden pont foka azonos, mondjuk 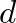 ? Kiderül, hgy ez nem lehetséges, ha
? Kiderül, hgy ez nem lehetséges, ha 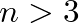 ; de ez már nem olyan egyszerű. Egy lehetséges megfogása a kérdésnek az, hogy a gráf tulajdonságait egy mátrixegyenletben foglaljuk össze:
; de ez már nem olyan egyszerű. Egy lehetséges megfogása a kérdésnek az, hogy a gráf tulajdonságait egy mátrixegyenletben foglaljuk össze:

ahol 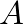 a gráf adjacencia-mátrixa,
a gráf adjacencia-mátrixa, 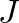 a csupa-
a csupa-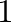 mátrix, és
mátrix, és 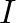 az egységmátrix (mindegyik mátrix
az egységmátrix (mindegyik mátrix 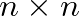 -es). A különböző bizonyítások ennek a mátrixegyenletnek a megoldhatatlanságát különböző módszerekkel mutatják meg: lehet vizsgálni
-es). A különböző bizonyítások ennek a mátrixegyenletnek a megoldhatatlanságát különböző módszerekkel mutatják meg: lehet vizsgálni 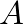 sajátértékeit, vagy hatványait, lehet dolgozni a valós test fölött vagy alkalmas véges test fölött, stb.
sajátértékeit, vagy hatványait, lehet dolgozni a valós test fölött vagy alkalmas véges test fölött, stb.
Ide csatlakozik a gráfelmélet egy fontos nagy területe, az erősen reguláris gráfok elmélete. Itt olyan gráfokat vizsgálunk, melyek regulárisak (minden csúcs foka azonos), és két csúcsnak vagy 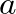 vagy
vagy 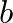 közös szomszédja van aszerint, hogy össze vannak-e kötve vagy nincsenek. A barátság tételhez azt kell megmutatni, hogy ha
közös szomszédja van aszerint, hogy össze vannak-e kötve vagy nincsenek. A barátság tételhez azt kell megmutatni, hogy ha 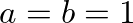 , akkor nincs ilyen gráf; de más
, akkor nincs ilyen gráf; de más 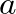 és
és 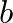 értékekhez már van. Nem megyünk bele ennek a részletezésébe, de egy konstrukciót érdemes bemutatni az erősen reguláris gráfok ürügyén.
értékekhez már van. Nem megyünk bele ennek a részletezésébe, de egy konstrukciót érdemes bemutatni az erősen reguláris gráfok ürügyén.
Tekintsük azt a gráfot, melynek csúcsai a 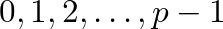 számok, ahol
számok, ahol 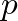 egy
egy 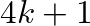 alakú prímszám. Az
alakú prímszám. Az 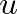 és
és 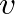 csúcsokat összekötjuük, ha van olyan
csúcsokat összekötjuük, ha van olyan 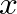 egész szám, melyre
egész szám, melyre 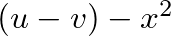 osztható
osztható 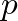 -vel (vagyis
-vel (vagyis 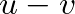 kvadratikus maradék). A
kvadratikus maradék). A  esetben az ötszöget kapjuk. Ezt a gráfot Paley-gráfnak nevezzük.
esetben az ötszöget kapjuk. Ezt a gráfot Paley-gráfnak nevezzük.
Elemi számelmélettel könnyű belátni, hogy a Paley-gráf minden csúcsa 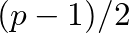 fokú. Csak kicsit nehezebb belátni, hogy két összekötött csúcsnak
fokú. Csak kicsit nehezebb belátni, hogy két összekötött csúcsnak 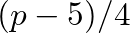 közös szomszédja van, két nem összekötött csúcsnak pedig
közös szomszédja van, két nem összekötött csúcsnak pedig 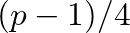 . Vagyis a Paley gráf erősen reguláris.
. Vagyis a Paley gráf erősen reguláris.
Ennél azonban fontosabb számunkra a következő észrevétel. Konstruáljunk a 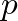 csúcson egy másik gráfot véletlenszerűen úgy, hogy bármely pontpárt (egymástól függetlenül)
csúcson egy másik gráfot véletlenszerűen úgy, hogy bármely pontpárt (egymástól függetlenül) 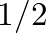 valószínűséggel kötünk össze. Így kapjuk az (
valószínűséggel kötünk össze. Így kapjuk az (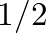 sűrűségű,
sűrűségű, 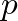 csúcsú) Erdős–Rényi véletlen gráfot. Ebben a gráfban bármely csúcs fokának a várható értéke
csúcsú) Erdős–Rényi véletlen gráfot. Ebben a gráfban bármely csúcs fokának a várható értéke 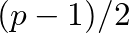 , és két csúcs közös szomszádainak várható száma
, és két csúcs közös szomszádainak várható száma 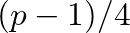 . A nagy számok törvényeinek segítségével be lehet látni, hogy ha
. A nagy számok törvényeinek segítségével be lehet látni, hogy ha 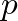 elég nagy, akkor a fokszámok és közös-szomszéd-számok mindegyike közel lesz a vérható értékéhez. Vagyis a véletlen gráf nagyon fog hasonlítani a Paley-gráfhoz, ha
elég nagy, akkor a fokszámok és közös-szomszéd-számok mindegyike közel lesz a vérható értékéhez. Vagyis a véletlen gráf nagyon fog hasonlítani a Paley-gráfhoz, ha 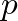 elég nagy.
elég nagy.
Ezzel el is jutottunk Sós Vera egyik központi kutatási témájához, a determinisztikus, véletlenszerű és véletlen struktúrák kapcsolatának, hasonlóságainak és különbségeinek vizsgálatához. Az egyenletes eloszlásokra vonatkozó számelméleti kutatásaiban is jelen van ez az általános kérdésfeltevés.
De a gráfoknál maradva, tekintsünk egy végtelen 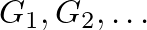 sorozatukat, ahol a
sorozatukat, ahol a 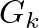 gráf
gráf 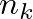 csúcsszámáról feltesszük, hogy
csúcsszámáról feltesszük, hogy 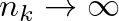 . A sorozatot
. A sorozatot 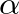 sűrűségű kvázivéletlennek nevezünk (
sűrűségű kvázivéletlennek nevezünk ( 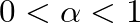 ), ha a következő teljesül: a
), ha a következő teljesül: a 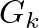 gráf minden fokszáma,
gráf minden fokszáma, 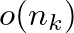 kivétellel,
kivétellel, 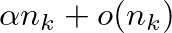 , és
, és  kivétellel, bármely két csúcs közös szomszédainak száma
kivétellel, bármely két csúcs közös szomszédainak száma 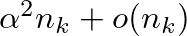 . (Az
. (Az 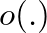 a
a 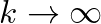 esetre vonatkozik.) A kvázivéletlen sorozat fogalmát Thomason [12] munkáját általánosítva Chung, Graham és Wilson [5] vezették be.
esetre vonatkozik.) A kvázivéletlen sorozat fogalmát Thomason [12] munkáját általánosítva Chung, Graham és Wilson [5] vezették be.
Ha minden 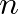 -re konstruálunk egy
-re konstruálunk egy 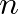 csúcsú,
csúcsú, 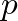 sűrűségű Erdős–Rényi véletlen gráfot, akkor ez a gráfsorozat
sűrűségű Erdős–Rényi véletlen gráfot, akkor ez a gráfsorozat 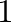 valószínűséggel kvázivéletlen lesz. A fentiekből látható, hogy a Paley-gráfok sorozata is kvázivéletlen. Sok más algebrai és számelméleti konstrukció is adható ilyen sorozatra.
valószínűséggel kvázivéletlen lesz. A fentiekből látható, hogy a Paley-gráfok sorozata is kvázivéletlen. Sok más algebrai és számelméleti konstrukció is adható ilyen sorozatra.
Kvázivéletlen gráfsorozatoknak igen sok jellemző tulajdonságuk van, például, hogy pontjaiknak minden 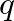 elemű halmazába
elemű halmazába 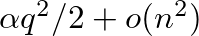 élük esik, vagyis az élek „szétterítettsége” elég jó. Legfontosabb a későbbiek szempontjából az, hogy minden rögzített
élük esik, vagyis az élek „szétterítettsége” elég jó. Legfontosabb a későbbiek szempontjából az, hogy minden rögzített 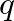 csúcsú,
csúcsú, 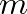 élű
élű 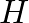 gráfra a
gráfra a 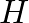 -val izomorf részgráfok száma a
-val izomorf részgráfok száma a 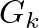 gráfban
gráfban  . Ami a legmeglepőbb, elegendő ezt csak két kis gráfra megkövetelni, nevezetesen az élre és a négyszögre.
. Ami a legmeglepőbb, elegendő ezt csak két kis gráfra megkövetelni, nevezetesen az élre és a négyszögre.
Nem sokkal később Simonovits Miklós és T. Sós Vera [10] is publikáltak egy fontos cikket a kvázivéletlen gráfokról, melyben a Szemerédi-féle regularitási lemmával hozták kapcsolatba. (Ez utóbbi kimondása nem fér egy ilyen köszöntő kereteibe.)
Gráflimeszek
2003-ban szinte egyidőben három kutató a Microsoft Research matematikai csoportjában három igen érdekes kérdést tett fel. Michael Freedman (Fields-érmes) azt kérdezte, hogy vajon milyen gráf-paraméterek jellemezhetők úgy, mint alkalmas statisztikus fizikai modellek partíció-függvényei. Jennifer Chayes (a csoport vezetője), a Barabási-Albert internet modellt vizsgálva kérdezte, hogy vajon értelmezhető-e egy véletlenszerűen növekedő gráfsorozat „határeloszlása” (a centrális határeloszlás-tételhez hasonlóan). T. Sós Vera (aki látogató volt a csoportnál) azt vetette fel, hogy hogyan lehet a kvázirandom gráfsorozatok jellemzéseit többosztályú kvázirandom gráfokra általánosítani.
Hamarosan kiderült, hogy a három kérdés szorosan összefügg egymással. A következő években Sós Vera rendszeres látogatója lett a csoportnak, és sok-sok időt töltöttünk (Christian Borgs, Jennifer Chayes, Sós Vera, Vesztergombi Katalin és én) a tábla előtt ülve vagy ácsorogva, kidolgozva a gráflimesz-elmélet alapjait. Sós Vera számelméleti kérdései és a véletlen–determinisztikus határvonalon szerzett tapasztalatai izgalmas elegyet alkottak Jennifer Chayes és Christian Borgs statisztikus fizikusi szemléletével és tudásával. Ritka a matematikában az ennyire meggyőzően „interdiszciplináris” közös kutatás.
Kicsit később bekapcsolódott a munkába Szegedy Balázs is (aki posztdok volt a csoportban). Az eredményeket több évvel később könyvben foglaltam össze, de mint oly sokszor, a téma első publikációi [1,2] talán jobban tükrözik az eredményekhez vezető utat. Freedman kérdését vele és Schrijverrel közös cikkben válaszoltuk meg, amit aztán más, algebrai irányban Szegedy Balázs és Schrijver továbbvitték. Sós Vera problémáját ennek az algebrai módszernek a felhasználásával vele közös cikkben sikerült megoldani [8]. Ezek a módszerek aztán beépültek a gráflimesz-elméletbe.
Látható ebből a rövid történeti áttekintésből, hogy akár a legalapvetőbb eredmények érthető előadására sem vállalkozhatok itt. De annyit meg kell tegyek, hogy bevezessem az alapvető definíciót, és két ábrán motiváljam.
Legyen 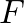 és
és  két véges gráf, és jelölje
két véges gráf, és jelölje  annak a valószínűségét, hogy egy véletlen
annak a valószínűségét, hogy egy véletlen  leképezés élt élbe visz. Akkor mondjuk, hogy egy
leképezés élt élbe visz. Akkor mondjuk, hogy egy 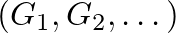 gráfsorozat konvergens, ha csúcsszámuk a végtelenhez tart, és a
gráfsorozat konvergens, ha csúcsszámuk a végtelenhez tart, és a 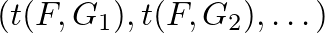 számsorozat minden
számsorozat minden 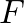 gráfra konvergens. Speciálisan, ha
gráfra konvergens. Speciálisan, ha 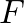 az egyetlen élből álló gráf, akkor ez azt jelenti, hogy az élsűrűségek sorozata konvergens.
az egyetlen élből álló gráf, akkor ez azt jelenti, hogy az élsűrűségek sorozata konvergens.
Minden kvázivéletlen gráfsorozat konvergens, de nagyon sok más, véletlen és determinisztikus gráfsorozat is konvergens. Minden végtelen gráfsorozatból kiválasztható egy konvergens részsorozat. A fogalom triviálissá válik, ha a 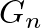 gráfok élsűrűsége 0-hoz tart, ezért általában fel lehet tenni, hogy a
gráfok élsűrűsége 0-hoz tart, ezért általában fel lehet tenni, hogy a 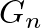 gráfok sűrűek (legalább const
gráfok sűrűek (legalább const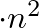 élük van).
élük van).
A fogalom erejét az adja, hogy igen sok ekvivalens módon is definiálható: két gráf „vágástávolsága” segítségével, statisztikus fizikai paraméterek konvergenciájával stb. Ezeket az ekvivalenciákat a [3,4] cikkekben dolgoztuk ki.
A 3. ábra bal oldalán egy elég egyszerű konvergens gráfsorozat, a félgráfok sorozatának egy tipikus tagja látható. A középső ábrát úgy kaptuk, hogy az adjacencia-mátrixban a 0-kat fehér, az 1-eket fekete négyzettel helyettesítettük. Ha a pontszámmal végtelenhez tartunk, a középső ábra egyre jobban hasonlít a jobb oldali ábrára.

3. ábra. A félgráfok, egy determinisztikus konvergens sorozat.
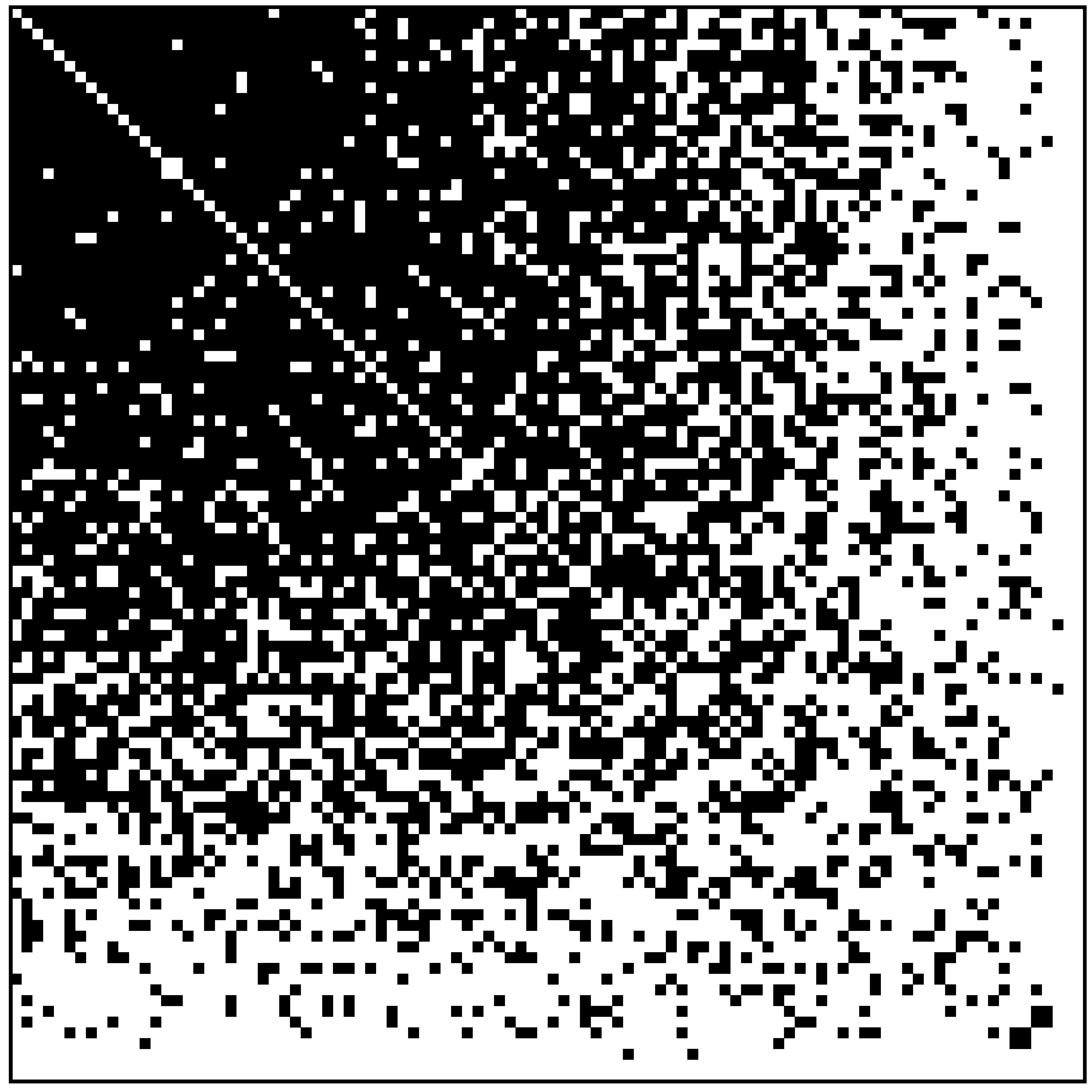
A 4. ábra bal oldalán egy egyszerű szabály szerint növekvő gráfsorozat látható (az adjacencia-mátrix szerinti ábrázolásban): az 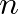 -edik lépésben egy új pontot veszünk hozzá, és leszórunk véletlenszerűen
-edik lépésben egy új pontot veszünk hozzá, és leszórunk véletlenszerűen 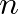 új élt. Az így kapott sorozat
új élt. Az így kapott sorozat 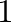 valószínűséggel konvergens lesz, és a pontszám növekedtével a jobboldali ábrához fog egyre jobban hasonlítani (ami a
valószínűséggel konvergens lesz, és a pontszám növekedtével a jobboldali ábrához fog egyre jobban hasonlítani (ami a 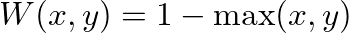 függvény szürkeárnyalatos ábrázolása).
függvény szürkeárnyalatos ábrázolása).
Ez a két példa talán érthetővé teszi, hogy minden konvergens gráfsorozatnak van egy limesz-objektuma, ami egy szimmetrikus, mérhető ![$W\colon [0,1]^2\to[0,1]$](/images/stories/latexuj/2020-08/2020-08-lovaszlaszlotsosvera/img72.png) függvény [9].
függvény [9].
 |
 |
4. ábra. Egy véletlenszerűen növekedő gráf, és ahova tart.
Utószó
Talán több helyet és időt töltöttem a gráflimeszekkel, mint az egy ilyen születésnapi köszöntőbe illene. De egyrészt meg akartam mutatni, hogy Sós Vera korábbi eredményei hogyan vezettek azokhoz a kérdésekhez, amik a gráflimesz-elmélet indulásában fontos szerepet játszottak, másrészt – és ez a fő – el akartam mondani, hogy milyen öröm volt együtt dolgozni ezen a témán. Majd' 40 évig tanított és mentorált engem, később folyóiratot, konferencia-köteteket szerkesztettünk, konferenciát szerveztünk együtt – de közös cikkünk nem volt. Ebben a témában aztán hat is lett.
Köszönöm a tanítást, támogatást, segítséget, közös munkát, és remélem és kívánom, hogy még sokáig kaphatok bölcs tanácsot, mély lényeglátást T. Sós Verától.
Irodalomjegyzék
- [1] C. Borgs, J.T. Chayes, L. Lovász, V.T. Sós, B. Szegedy and K. Vesztergombi: Graph Limits and Parameter Testing, STOC38 (2006), 261–270.
[2] C. Borgs, J. Chayes, L. Lovász, V.T. Sós and K. Vesztergombi: Counting graph homomorphisms, in: Topics in Discrete Mathematics (ed. M. Klazar, J. Kratochvil, M. Loebl, J. Matoušek, R. Thomas, P. Valtr), Springer (2006), 315–371.
[3] C. Borgs, J.T. Chayes, L. Lovász, V.T. Sós and K. Vesztergombi: Convergent Graph Sequences I: Subgraph frequencies, metric properties, and testing, Advances in Math. 219 (2008), 1801–1851.
[4] C. Borgs, J.T. Chayes, L. Lovász, V.T. Sós and K. Vesztergombi: Convergent Graph Sequences II: Multiway Cuts and Statistical Physics, Annals of Math. 176 (2012), 151–219.
[5] F. R. K. Chung, R.L. Graham and R.M. Wilson: Quasi-random graphs, Combinatorica 9 (1989), 345–362.
[6] P. Erdős, A. Rényi, and V.T. Sós: On a problem of graph theory, Studia Sci. Math. 1 (1966), 215–235.
[7] M. Freedman, L. Lovász and A. Schrijver: Reflection positivity, rank connectivity, and homomorphisms of graphs, J. Amer. Math. Soc. 20 (2007), 37–51.
[8] L. Lovász and V.T. Sós: Generalized quasirandom graphs, J. Combin. Theory B 98 (2008), 146–163.
[9] L. Lovász and B. Szegedy: Limits of dense graph sequences, J. Combin. Theory B 96 (2006), 933–957.
[10] M. Simonovits and V.T. Sós: Szemerédi's partition and quasirandomness, Random Struc. Alg. 2 (1991), 1–10.
[11] V. T. Sós: On the distribution mod 1 of the sequence 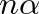 , Ann. Univ. Sci. Eötvös Sect. Math. 1 (1958), 127–134.
, Ann. Univ. Sci. Eötvös Sect. Math. 1 (1958), 127–134.
[12] A. Thomason: Pseudorandom graphs, in: Random graphs '85 North-Holland Math. Stud. 144, North-Holland, Amsterdam, 1987, 307–331.
Lovász László









