Petr Beckmann: A Pi története

Hajós György máig nevezetes, Elemi geometria című könyvében két olyan rész van, amely egyetlen olvasás után is az emlékezetembe vésődött. Az egyik az Euler-féle poliédertétel bizonyítása egy bolygó elképzelésével és gátak robbantásával. A mai napig úgy tudom felidézni magát a tételt, hogy a gondolatmenetre emlékszem. A másik ilyen rész egy kis betűkkel szerénykedő tétel a kör kerületével kapcsolatos fejezetben:

Tétel. Ha 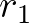és 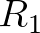egy szabályos sokszög beírt és körülírt körének sugarát jelöli, akkor az ugyanakkora kerületű s kétennyi oldalú szabályos sokszög beírt és körülírt köreinek 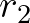és 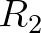sugarát a következő képletek adják:

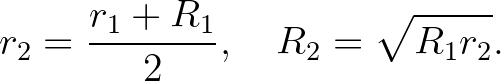
Miért is emlékezetes ez? Ehhez egy kicsit a tétel következményeibe érdemes magunkat beleásnunk. Definiáljuk az 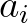sorozat tagjait rekurzióval a következőképpen:

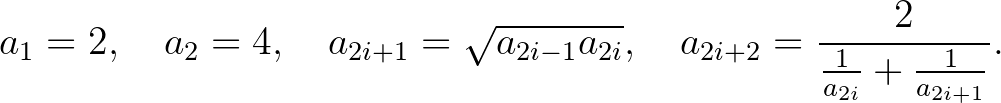
A fenti, elemi geometriai tételről aligha gondolnák sokan, hogy bármit köze lenne a sorozat határétékéhez, de valójában a segítségével könnyen belátható, hogy

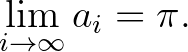
Nem csodálatos? Két egész számból kiindulva, felváltva geometriai és harmonikus közepeket számolva nevezetes, transzcendens határértéket kapunk. A bizonyítási trükk annyi, hogy egy négyzet kerületéből elindulva a sokszög oldalszámának minden határon túl menő kétszerezése kört eredményez majd. De lehet más kiindulási értkekeket is választani az iterációhoz; az

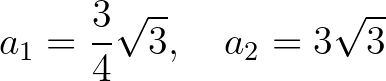
kezdeti értékpárt használva a határérték szintén 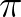lesz. Itt szabályos háromszögből kezdtük a gondolatmenetet. Talán még nem unalmas, ha a szabályos ötszögből induló két kezdeti szám is szerepel itt, amikor szintén 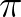adódik határétékként:

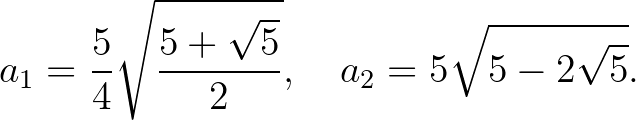
Ha a Hajós-könyvben szereplő tétel ennyire könnyen ragadt meg bennem, akkor talán az sem váratlan, hogy amikor egy könyvesboltban megláttam Petr Beckmann A Pi története című könyvét, azonnal belekerült a bevásárlókosáramba. Az eredeti művet először 1970-ben (!) adták ki, a magyar fordítást a Typotex Kiadó viszont csak 2022-ben jelentette meg Gerner József fordításában. Szerencsére a krónikájának időskálája évezredes, amihez képest az eredeti mű kiadása óta eltelt ötven év igazán semmiség.

A szerző, Petr Beckmann (1924–1993) Prágában született, a második világháború alatt a brit Royal Air Force-nál szolgált, majd szülőhazájában villamosmérnöki képesítést szerzett. 1962-től a University of Colorado professzoraként dolgozott Boulderben. Számos könyvet írt, s pályafutása végén arról is nevezetes lett, hogy kétségbe vonta Einstein speciális reltivitáselméletét. Úgy tűnik, ezen érvei nem lehettek túlságosan meggyőzőek, viszont ez a megállapítás a A Pí történetére a legkevésbé sem vonatkozik, amely sodró lendületű írásmű.

Sem a bevezetőben említett tétel a Hajós-könyvből, sem az utána rekurzívan definiált sorozat nem szerepel ebben a krónikában – legalábbis nem szó szerint. Azt viszont megtudtam, hogy a kör kerületének sokszögekre alapuló közelítése a görög matematika, egészen pontosan a szofista filozófus, rhamnoszi Antiphón (i.e. kb. 480–i.e. 411) ötlete volt. Az elvet a gyakorlatban is használhatóvá a szürakuszai Arkhimédész (i.e. kb. 287–i.e. 212) tette, aki 96 oldalú sokszöggel, tehát háromszögből indulva adott alsó és felső határt is a 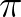értékére:

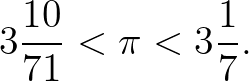
A görögök azonban a végtelentől való, nem is egészen megalapozatlan filozófiai félelmük miatt (elég csak Zénón paradoxonaira gondolni), a határérték jelentőségét nem ismerték fel.

A könyv 18 fejezetet tartalmaz, majd a végén, egyetlen oldalon a értékének első tízezer tizedesjegyét adja meg mindössze két nyomtatott oldalon, természetesen elég apró számjegyekkel. A szerző nemigen próbál értékítéletektől mentesen írni a tudományos felfedezésekről, és ez szerintem nagy hasznára van a könyvnek. A Római Birodalom történelmi szerepéről, illetve Arisztotelészről például olyan, vaskosan negatív véleményt olvashatunk, amely más (tudomány)történeti munkákban nemigen lelhető fel. Talán szokatlan ez, de mindenképpen elgondolkodtató és eredeti – időnként még meggyőző is. A tanulmány hatására például újra elolvastam, hogy Simonyi Károly monumentális, A fizika kultúrtörténete című műve mit ír Arisztotelész munkásságáról. Amit találtam róla a könyvben, értékítéletektől mentesen ugyan, de szinte semmi másról nem szól, csak a görög filozófus valóban nagy hatású tévedéseiről. A legközvetlenebbül a mozgástan esetében érhető ez tetten, amiről Simonyi a következőt írta: „Az arisztotelészi dinamikán, amely közel kétezer évig a tudomány végső szava volt ezen a téren, az emberiség csak úgy tudott túllépni, hogy az egész arisztotelészi világképet elvetette. Általánosságban tehát azt mondhatjuk, hogy a jelenségek felületét ugyan hűen ábrázoló és rendszerező, de a mélyre egyáltalában nem hatoló peripatetikus mozgástan a dinamika tudományának fejlődését inkább gátolta, mint elősegítette.”

De térjünk vissza Beckmannhoz és a 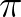-hez! A szerző nemcsak világos értékítéletet mond, hanem a politikai korrektség látszatát is elkerüli az egyházak szerepének megítélésében a tudomány történetében. 1970-ben ezt még könnyebb volt megtenni, mint manapság? Például: „Három jelentős esetről tudunk, amikor a vallás agresszívvá vált, s az emberiség nagy részét hosszan tartó, szörnyűséges rémálomba taszította. Ez a középkori kereszténység, a középkori iszlám, és a modern kommunizmus.” Talán nem meglepő egy ilyen vélemény valakitől, aki 1962-ben távozott Csehszlovákiából Amerikába. A következő, váratlan analógia is valószínleg megragad majd az olvasó fejében: „A szovjet főpapok a Pravdát nyomtatták ki a köznépnek, ők maguk viszont a New York Times kivonatát olvasták; ugyanígy tett a középkori papság is: a matematikát sátáninak bélygezték a tömegek előtt, ők maguk viszont sűrűn megmártóztak ebben a fertőben.”

Talán úgy tűnhet, ennyi érdekesség után a matematikai tartalom szerepe csak másodlagos maradhat. De nem így van. A könyv valóban számtani-mértani történetmesélés, de párhuzamos módszert használ. Lényegében öt szál fut, némelyik a kőkorszaktól kezdődőden, amikor kettőnél tovább nem nagyon számolt még az ember. Ennek a ténynek egy érdekes kulturális tükröződése, hogy a legtöbb nyelvben a kettő és a fél szavak eredete nagyon különböző, de az összes többi tört nevét az egész számokból származtatják.

Az első visszatérő téma a 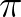számértékének minél pontosabb meghatározása. Könnyen egyet lehet érteni a szerzővel abban, hogy ennek tíz tizedes jegyen túl semmiféle gyakorlati haszna nincsen, de intellektuális gyakorlatnak gyönyörködtető, ezért sokan fektettek bele energiát. A számérték meghatározása általában a többi visszatérő szállal is kapcsolatban van. Az ilyen számjegyvadászok leghíresebbike a holland Ludolph van Ceulen (1539–1610), aki 1596-ban a már említett, sokszögkettőzős módszert 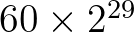oldalú síkidomra használva 20 helyes jegyet kapott. Ezért – különösen német nyelvterületen – a 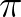-t időnként még ma is Ludolph-féle számnak (die Ludolphsche Zahl) nevezik. Szintén ezt a munkát örökíti meg a következő magyar nyelvű mondat, amelyet én segédeszközként használok arra, hogy a 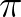húsz számjegyére fejből emlékezzek:

Nem a régi, s durva közelítés, mi szótól szóig így kijön betűiket számlálva; Ludolph eredménye már, ha itt végezzük húsz jegyen. (3,14159265358979323846)

Ez a mondat természetesen nincs benne Beckmann könyvében, de hasonlóan használható 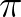-verseket olvashatunk benne angolul:

How I want a drink, alcoholic of course, after the heavy lectures involving quantum mechanics!

Vagy franciául:

Que j'aime afaire apprendre un nombre utile aux sages!
Immortel Archimede, artiste ingenieur.
Qui de ton jugement peut priser la valeur?
Pour moi. ton probleme eut de pareils avantages.

Vagy németül:

Dir, o Held, o alter Philosoph, du Riesengenie!
Wie viele Tausende bewundem Geister
Himmlisch wie du und gottlich!
Noch reiner in Aeonen
Wird das uns strahlen
Wie im lichten Morgenrot!

Az ilyenek létezéséről már középiskolás koromban tudtam, de csak a könyv hatására gondolkodtam el azon, hogy vajon mi történik akkor, ha éppen nulla számjegy következik. Ezt nem sikerült kiderítenem, de én minden bizonnyal tíz betűs szót használnék. Viszont emiatt ellenőriztem: a 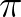számjegyei között a tizedes vesszőtől jobbra a 32. helyen szerepel először 0. Hármasból pédául öt is van előtte, és akkor a tizedes vesszőtől balra lévőt még nem is számoltuk.

A második nagy visszatérű téma a sokszögoldal-felező eljárás, de erről már volt szó. A harmadik a kör négyszögesítése, vagyis egy négyzettel egyenlő kerületű (vagy területű) kör szerkesztése. Erre egyébként számos látszólag sikeres megoldást mutat be a mű, de mindegyiknél megtudjuk azt is, hol nem felel meg az eukleidészi szerkesztés szabályainak. Persze idővel igazolták, hogy ezen korlátok között a feladat nem oldható meg, viszont néhány, a logikát látványosan elutasító ember még a bizonyítás közismertté válása után is próbálkozott vele, Beckamnn tőlük sem sajnálja a kritikai szavakat.

A negyedik lényeges téma a 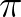irracionális, illetve transzcendens voltának bizonyítása. Az előbbi Johann Heinrich Lambert (1728–1777) és Adrien-Marie Legendre (1752–1833) érdeme. Tették mindezt még jóval azelőtt, hogy Joseph Liouville (1809–1882) a transzcendens számok puszta létezését bebizonyította volna 1840-ben. A 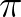-re a bizonyítást Carl Louis Ferdinand von Lindemann (1852–1939) találta meg 1882-ben, ezzel egyúttal a kör négyszögesítésének lehetlenségét is igazolta.

Az ötödik, s egyben az én listámon az utolsó visszatérő téma a 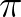-re vonatkozó algebrai kifejezések megtalálása. Ennek kapcsán megtudjuk azt is, hogy Beckmann szerint minden idők legnagyobb matematikusa Leonhard Euler (1707–1783) volt és nem Carl Friedrich Gauss (1777–1855). Az ő koruktól kezdve számos lánctörtet és végtelenben vett határértéket hoztak kapcsolatba a 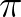-vel. Ilyen környezeteben derül ki az is, hogy számítógépekkel a 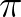sok százezer számjegyének meghatározását a következő összefüggés alapján végezték:

Végezetül emlékezzünk meg arról is, hogy természettudományos körökben a politikusok negatív megítélését gyakran olyan viccekkel is kifejezik, amely szerint egy-egy törvényhozás vagy kormány abszurd, a természeti törvényeknek ellentmondó emberi szabályt akar hozni (például egy változat: az amerikai törvényhozás tegnap felfüggesztette a gravitáció törvényét). Ez persze soha nem nyugszik valós történeti alapokon. Vagy mégis? Beckmann például előásta az Indiana állam képviselőháza elé 1897. január 18-án beterjeszett, 246-os számú javaslatot, amelynek a címe Törvényjavaslat egy új matematikai igazság bevezetésére volt. Ebben például a következő bekezdés is szerepelt:

Indiana állam közgyűlése iktassa törvénybe, hogy a kör területe úgy aránylik a kerület negyedével megegyező vonal négyzetéhez, ahogy az egyenlő oldalú téglalap területe aránylik az egyik oldal négyzetéhez. Az átmérő lineáris egységként való alkalmazása a körterület kiszámításában a jelen szabály értelmében teljes egészében helytelen

Ha átsiklunk afelett, hogy az „egyenlő oldalú téglalap” tisztességes nevén négyzet, akkor a szöveg éppen 4-et ad a 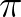értékére. Ha viszont Petr Beckmannt követve elírásra gyanakszunk, és egyenlő oldalú háromszöget képzelünk erre a helyre, akkor 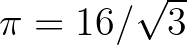, adódna, ami még 9-nél is nagyobb.

1897. febrár 5-én a ház egyhangúlag, 67 támogató szavazattal elfogadta a javaslatot. Szerencsére néhány nappal később C. A. Waldo, a Purdue egyetem matematikaprofesszora véletlenül a parlamentbe látogatott, s néhány törvényhozónak kifejtette ellenvéleményét. Ennek hatására a végleges szavazást Indiana állam szenátusában 1897. február 12-én határozatlan időre elnapolták. Beckmann 1970-ben született könyve megjegyzi, hogy azóta sem tűzték napirendre.

2024-ben hozzátehetjük, hogy ez az állapot szerencsére az azóta elmúlt 54 évben sem változott.