
Katz Sándor: Hatványok, gyökök ‒ középszinten, emelt szinten, versenyszinten, I. és II. kötet, Matematikai Tehetségekért Alapítvány, Nagykanizsa 2023.
Egy olyan különleges szakmai könyvet, feladatgyűjteményt, összefoglalást vehet kézbe az olvasó, amelyhez hasonló munkával az utóbbi évtizedekben nem találkoztam.
Az internet az elmúlt évtizedekben elhozta a matematika tanításában is a megfoghatatlan mennyiségű információt, a felgyorsult ismeretszerzést. A tanulók és a tanárok a bőség zavarában nem kapnak világos üzeneteket a feladatok nehézségi szintjéről, a logikai kapcsolatokról, a célszerű felépítésről. A szakmai könyvek vagy sok-sok érdekes témakörben, egymástól egészen távoleső módszereket, ismereteket nyújtanak, keresztmetszetet adnak, vagy közvetlenül az érettségi vizsgákra készítenek fel.
Ezek mellett a Matematikai Tehetségekért Alapítványnál korábban jelent meg két összefoglaló ‒ elméleti ismereteket és tematikus feladatgyűjteményt tartalmazó ‒ jellegű munka az egyenletekről és az egyenlőtlenségekről.
Ez a könyv azonban egészen másként közelíti meg a hatványok és gyökök témakörét. Igyekszik minden részletre kiterjedően áttekintést adni a módszerekről és az alkalmazásokról egészen a középszintű érettségitől az olimpiai feladatok szintjéig. Teljességre törekszik a szó legklasszikusabb értelmében. Az érettségi követelményeit meghaladó fejezetek elején egy-egy alapos elméleti összefoglalót is kapunk a kidolgozott mintapéldák előtt.
Dr. Katz Sándor Príma Primissima és Rátz Tanár Úr Életműdíjas matematikatanár közel 50 éves gimnáziumi működése alatt országos hírű matematikai tehetséggondozó műhelyt hozott létre Bonyhádon, a Petőfi Sándor Evangélikus Gimnáziumban. Munkájának eredményét több száz versenyeredmény, azóta végzett kiváló tanárok, matematikusok, fizikusok, informatikusok több generációja jelzi.
Tanári munkája során évtizedeken keresztül nagyon gondosan, osztályozva gyűjtötte a feladatokat a legkülönbözőbb forrásokból. Ezekből aztán a tanulók és az órák céljaihoz a igazodó feladatsorokat állított össze. Ez a teljes elemi matematikát átfogó gyűjteménye több tucat ehhez hasonló méretű kétkötetes, 750 oldalas könyvet is megtöltene. Ennek most csak egy kisebb szeletét tárta elénk Katz tanár úr ebben a munkában.
Az első kötetben a történeti bevezető, az elméleti összefoglaló és az alkalmazások tárgyalása az emelt szintű szóbeli érettségire való felkészülést segítik, ez példaként szolgálhat más témakörök feldolgozásánál is. Az első kötetben 17 fejezetben tekinti át a szerző a megoldási módszereket. Ezeket néha tételek formájában, de legtöbbször részletesen kidolgozott mintapéldákban ismerjük meg. A kidolgozott tételek, alkalmazások, mintapéldák száma több mint 425, a hatványok közvetlen alkalmazásaitól a paraméteres gyökös egyenlőtlenségekig.
A második kötet egy tematikus feladatgyűjtemény, amelyben az első kötetnek megfelelő felosztásban, 17 fejezetben 529 feladatot találunk. A feladatok mindegyikéhez megoldás és sokszor kiegészítő megjegyzés, kereszthivatkozás, általánosítás is tartozik.
Ezek a számok is mutatják, hogy mennyire alapos, lehetőség szerint minden előforduló módszerre kiterjedő, tudatos válogatás ez.
A feladatoknál lehetőség szerint mindenütt megjelölte a szerző a forrást. (A felsorolásban 26 ilyen forrás szerepel!)
A két kötet nagyon sokféleképpen használható. Használhatják tanár kollégák órai, szakköri felkészüléshez, tanulók ismereteik bővítéséhez, gyakorláshoz, érettségi felkészülésükhez, de a legkiválóbb versenyzők is önálló munkához.
A hatványok és a gyökök csak egy kicsiny szeletét jelentik a középiskolai matematika tananyagnak. A könyv azonban a feladatmegoldási ötletek, módszerek sokaságát vonultatja fel, amelyek más témakörökben is kiválóan használhatók.
Akár csak részleges feldolgozása is sok intellektuális élményt, használható ismeretet nyújt.
Végezetül két feladat a feladatgyűjteményből, amelyek véleményem szerint felvillantják a feladatok változatosságát és a nehézségét is:
1. Négy számról 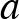 -ról,
-ról, 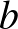 -ről,
-ről, 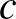 -ről és
-ről és 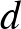 -ről tudjuk, hogy a belőlük képezhető hat darab kéttagú összeg közül három racionális, három pedig irracionális értékű.
-ről tudjuk, hogy a belőlük képezhető hat darab kéttagú összeg közül három racionális, három pedig irracionális értékű.
a) Racionális szám-e az  összeg?
összeg?
b) Hány racionális szám lehet a négy szám között?
2*. 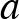 ,
, 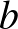 ,
, 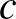 ,
, 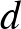 ,
, 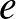 legyenek a
legyenek a ![$\left[p,q\right]$](/images/stories/latexuj/2024-08/2024-08-hatvanyokgyokok/img7.png) intervallum elemei, ahol
intervallum elemei, ahol 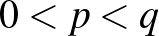 .
.
Igazoljuk, hogy
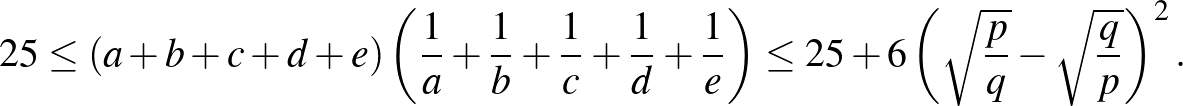
Kiss Géza
Budapesti Fazekas Mihály Gyakorló Általános Iskola és Gimnázium











