A Bolyai Társulat 2022-es évi díjai

Beke Manó Emlékdíj

A BJMT minden évben kiosztott díjai közül a legrégebbi a Beke Manó Emlékdíj, amely hosszabb időn át végzett kiváló és eredményes matematikai nevelő-oktató munkáért adható ki. 2022-ben a nyár elején megrendezésre került Rátz László Vándorgyűlésen osztották ki a Beke Manó díjakat. A díjazottak:

Burom Mária,

Göncfalviné Cseh Éva,

Kiss Zoltán,

Nagyné Lelkes Ildikó,

Szántó Zsuzsanna,

Székeli Andrea,

Tóth Mariann.

Méltatásukat a https://www.bolyai.hu/dijak-beke-mano-emlekdij oldalon olvashatják.

2022. december 16-án került sor a további díjak átadására és a Schweitzer és Kürschák versenyek eredményhirdetésére a Rényi Alfréd Matematikai Kutatóintézet Nagytermében.

Szele Tibor Emlékérem

A 2022. évi Szele Tibor Emlékérem kitüntetettje Hajdu Lajos, a Debreceni Egyetem Matematikai Intézetének egyetemi tanára, az MTA doktora.

Hajdu Lajos rendkívül tehetséges, sikeres és sokoldalú matematikus, aki a tudományos utánpótlásnevelés területén is igen komoly eredményeket tud felmutatni. Fő kutatási területe a diofantikus számelmélet, amelyben számos fontos, nagyhatású eredményt publikált szerteágazó területeken. Tudományos tevékenységének nemzetközi visszhangja igen jelentős. Tudományszervezői, tehetséggondozói és témavezetői tevékenysége is kimagasló, amelynek itt olvashatják részleteit.

Hajdu Lajos a Szele Tibor Emlékéremmel

Grünwald Géza Emlékérem

2022-ben a Grünwald Géza Emlékérmet a matematikai alapkutatásban kiemelkedő fiatal, az 1992-ben született Damásdi Gábor kapta. Matematikus alap-, majd mesterszakos tanulmányait az Eötvös Loránd Tudományegyetemen végezte, majd 2018-tól ugyanitt doktori hallgató. Jelenleg az ELTE Matematikai Intézet doktorandusza és tanársegédje, valamint a Rényi Alfréd Matematikai Kutatóintézet tudományos segédmunkatársa.

Damásdi Gábornak 9 cikke jelent meg nemzetközi folyóiratokban, további 4 pedig konferenciakötetekben. Főleg kombinatorikai, illetve diszkrét geometriai kérdéseken dolgozik, eredményei közül több a téma legrangosabb fórumain került publikálásra. Önálló munkájában sikerült igazolnia egy, a Hadwiger-Nelson problémához kapcsolódó sejtést, megmutatva, hogy az ún. odd wheel gráfok nem páratlan távolság gráfok. Több cikkében bizonyos geometriai hipergráfok polikromatikus színezéseivel foglalkozik. Pach, Tardos és Tóth egy korábbi eredményét kiterjesztve megmutatta, hogy bármely m-hez létezik olyan síkbeli ponthalmaz, amelyet bárhogyan is színezünk 3 színnel, lesz a pontok között m darab, amelyek egyszínűek, és elválaszthatóak a többi ponttól egy kör segítségével. Nemrég azt is sikerült igazolnia, hogy hasonló konstrukció egységkörökkel, sőt, semelyik síkbeli konvex halmaz eltoltjaival sem lehetséges. Ennek bizonyításához a közelmúltban Bousquet, Lochet és Thomassé által bizonyított Erdős−Sands−Sauer−Woodrow sejtés egy általánosítását is belátta, valamint a probléma és a híres Hadwiger-féle megvilágítási sejtés közötti összefüggést is igazolta.

Farkas Gyula Emlékdíj

A Farkas Gyula Emlékdíjat olyan kutatók kaphatják meg, akik 35-ik életévüket még nem töltötték be, lehetőleg PhD fokozattal rendelkeznek, és jelentős tudományos tevékenységet folytattak az alkalmazott matematika területén. 2022-ben a négy díjazott:

Baráth Dániel (ETH Zürich),

Cseh Ágnes (KRTK Közgazdaságtudományi Intézet),

Juhász Nóra (SZTE Bolyai Intézet),

Horváth Márkó (SZTAKI).

Méltatásukat itt tekinthetik meg.

Rényi Kató Emlékdíj

2022-ben a Bolyai János Matematikai Társulat négy jelöltnek ítélte oda a Rényi Kató Emlékdíjat.

Jung Attila a díj I. fokozatát, Grünfelder Balázs, Tóth Péter és Vékássy Áron pedig a díj II. fokozatát nyerte el.

Jung Attila az Eötvös Loránd Tudományegyetem Matematika Doktori Iskolájának elsőéves hallgatója. Már BSc hallgatóként aktív kutatói tevékenységet végzett témavezetőjével, Naszódi Mártonnal. Először Helly-típusú tételekre adtak kvantitatív becslést, mely hiányterületnek számít az adott témában. Az ebből készült tanulmányt TDK első díjjal, OTDK harmadik díjjal jutalmazták, az eredményeket bemutató cikk a rangos European Journal of Combinatorics-ban jelent meg.

Ezen eredmények folytatása és bizonyos értelemben általánosítása az a munka, amely hipergráf láncok Helly-típusú tételeivel foglalkozik. Itt ismert egzisztencia tételekre adott kvalitatív becslést, mely bizonyos esetekben éles is. Ezen eredmények a 34. Canadian Conference of Computation Geometry konferencián kerültek bemutatásra.

Emellett megemlítendő, hogy Jung Attila megoldott egy Katona O.H. Gyula által felvetett kérdést is hipergráfok árnyékával kapcsolatban.

Grünfelder Balázs a Szegedi Tudományegyetem Matematika Doktori Iskolájának elsőéves hallgatója. Egyetemi tanulmányai alatt kezdett témavezetőjével, Fodor Ferenccel, sztochasztikus geometriai kérdésekkel foglalkozni. Kutatása, mely síkbeli alakzatok általánosított véletlen sokszögekkel való közelítésének aszimptotikus tulajdonságait vizsgálja, a sztochasztikus geometria egy aktívan kutatott területe. Eme munkában elsősorban egy sima határú síkbeli konvex alakzat véletlen részhalmazainak speciális konvex burkát tanulmányozták. Ezen konvex burok szögeinek számának szórására, illetve a kimaradó terület szórására adtak éles alsó becslést, melyet összevetve a korábban ismert felső korlátokkal megállapítható a pontos nagyságrend. Az eredményekből készült publikáció a rangos Documenta Mathematica folyóiratban jelent meg. Emellett a jelölt TDK első díjat és OTDK Különdíjat kapott az ehhez kapcsolódó munkájáért.

Tóth Péter a Debreceni Egyetem Matematika- és Számítástudományok Doktori Iskolájának elsőéves hallgatója. Kutatásai során Boros Zoltán témavezetése mellett először olyan teljesen rendezett halmazokat konstruált, melyekben igaz a Cantor-axióma és a nyílt metszet tulajdonság, ám nem teljes, azaz nem teljesíti a legkisebb felső korlát tulajdonságot. Az eredményeket TDK első és OTDK második díjjal jutalmazták, emellett a Mathematica Pannonica folyóiratban kerültek közlésre. A jelölt másik, önálló kutatása Boros Zoltán kétdimenziós függvényegyenletek folytonos megoldásainak karakterizációjára vonatkozó eredményeit általánosítja magasabb dimenzióban. Az egyik fő eredmény, hogy bevezeti az eltolás-invariáns függvény fogalmát, melyet karakterizál és aminek segítségével elegáns módon összeköti a korábban vizsgált fogalmakat, megoldva az eredeti kérdést magasabb dimenzióban. Az elért eredmények az Aequationes Mathematicae folyóiratban jelentek meg, valamint magyar és nemzetközi konferenciákon kerültek bemutatásra.

Vékássy Áron a Budapest Műszaki Egyetem elsőéves villamosmérnök MSc diákja. Fiatal kora ellenére már számos cikk szerzője, melyeket témavezetőjével, Recski Andrással együtt közölt. A kutatásában összetett villamos hálózatokat vizsgál lineáris algebrai, gráf- és matroidelméleti eszközökkel. A bemutatott eredmények nem ritkán meglepőek, mint például a paraméterek általános választása mellett a rendszer leírására használt mátrixok rangjának növekedése. Emellett több érdekes új fogalmat vezettek be, mint például az általánosított n-kapukat, és azokat matematikai precizitással vizsgálták, elsősorban matroidelméleti eszközökkel. A jelölt jól kombinálja matematikai ismereteit a szakterület legfrissebb eredményeivel és módszereivel, valamint kiváló mérnöki intuíciójával. Az elért eredmények nemzetközileg elismert mérnök tudományokkal foglalkozó folyóiratokban jelentek meg.

A Rényi Kató Emlékdíjakat Fleiner Tamás és Simon Péter adta át.

Patai-díj

A Patai Alapítvány 2022. évi díját a Bolyai Társulat bizottsága Lócska Orsolya Dóra részére ítélte oda az alábbi indoklással.

Lócska Orsolya Dóra a debreceni Kölcsey Ferenc Református Gyakorló Általános Iskola matematika és vizuális kultúra tanára. 2020-tól a Debreceni Egyetem Matematika- és Számitástudományok Doktori Iskola hallgatója. Kutatási témája az algebrai gondolkodásmód fejlesztése felső tagozatos korosztályban. Lócska Orsolya Dóra már egyetemi hallgatóként bekapcsolódott a matematika-didaktikai kutatásokba. Ezen munkája elismeréseként a XXXIII. OTDK-n dolgozatára különdíjat kapott. Később az Új Nemzeti Kiválóság Program ösztöndíjasaként folytatott kutatómunkát, amely eredményeit Magyarországon megjelent, de angol nyelvű folyóiratban publikálta. Előadást tartott a CERME konferencián, és az előadása alapján készült dolgozat publikálására is lehetőséget kapott. Jelenleg két további publikációja is előkészítés alatt áll.

PhD hallgatóként egyetemi hallgatók számára is tart tanórákat a Debreceni Egyetemen. Munkája során széleskörű szakmai kapcsolatot tart a hazai matematika-didaktika kutatóközösséggel. Jelenleg több intézmény matematikatanárainak bevonásával végzi saját kutatásait az MTA Közoktatás-fejlesztési Programjának keretein belül. Aktív tudásmegosztó tevékenységet is végez, legutóbb a saját szakmai kutatásainak az eredményeiről adott elő a Vezetőtanítók és Vezetőtanárok XIV. Országos Módszertani Konferenciáján.

A díjátadó résztvevői

A 2022. évi Kürschák József Matematikai Tanulóversenyről

A Bolyai János Matematikai Társulat a 2022. évi Kürschák József Matematikai Tanulóversenyt október 7-én 14 órai kezdettel rendezte meg. A Társulat elnöksége a verseny lebonyolítására az alábbi bizottságot kérte fel: Biró András, Frenkel Péter, Harangi Viktor, Kovács Benedek, Maga Péter (titkár), Pach Péter Pál (elnök), Tóth Géza.

A bizottság a következő feladatokat tűzte ki:

1. Egy négyzetet felbontottunk 2022 téglalapra (úgy, hogy semelyik két téglalapnak nincs közös belső pontja). Tekintsük az összes téglalap összes oldalegyenesét. Maximálisan hány különböző egyenest kaphatunk?

2. Tegyük fel, hogy a 4-gyel osztva 3 maradékot adó 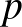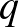$p$ , $q$ prímszámokra az 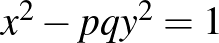$x^2-pqy^2=1$ egyenletnek van pozitív egész 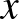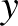$x$ , $y$ megoldása. Igazoljuk, hogy a 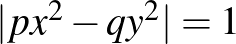$\vert px^2-qy^2\vert=1$ egyenletnek is van pozitív egész 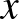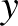$x$ , $y$ megoldása.

3. Legyen 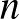$n$ pozitív egész szám. Bizonyítsuk be, hogy ha az 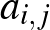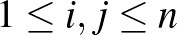$a_{i,j}$ ( $1 \leq i,j \leq n$ ) valós számokra 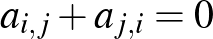$a_{i,j}+a_{j,i}=0$ minden 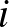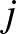$i$ , $j$ esetén (speciálisan 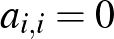$a_{i,i}=0$ minden $i$ -re), akkor fennáll az alábbi egyenlőtlenség:

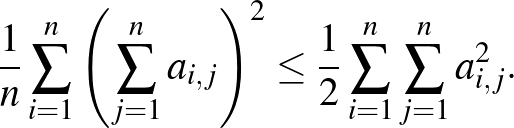
$\displaystyle \frac{1}{n} \sum_{i=1}^n \left( \sum_{j=1}^n a_{i,j} \right)^2 \leq \frac{1}{2} \sum_{i=1}^n \sum_{j=1}^n a_{i,j}^2.$

Mikor áll fenn egyenlőség?

Az idei versenyre 115-en regisztráltak, akiktől végül összesen 93 dolgozat érkezett be. Az első feladatra közel 40 lényegében teljes megoldás érkezett, a második feladatot 8-an, a harmadik feladatot pedig 7-en oldották meg helyesen vagy lényegében helyesen. Két versenyző helyesen oldotta meg az első két feladatot, és apró hiányosságtól eltekintve a harmadik feladatra is helyes megoldást adott. Ezért

I. díjban és 55 000 Ft pénzjutalomban részesül

Jánosik Máté, a győri Révai Miklós Gimnázium érettségizett tanulója (tanárai Árki Tamás, Nagy Róbert és Pósa Lajos),

Lovas Márton, a Békásmegyeri Veres Péter Gimnázium 12. osztályos tanulója (tanárai Simon János és Szűcs Gábor).

Egy versenyző helyesen oldotta meg a harmadik feladatot és hiányosságoktól eltekintve megoldotta az első és második feladatokat. Ezért a teljesítményért

II. díjban és 40 000 Ft pénzjutalomban részesül

Németh Márton Tamás, a Budapesti Fazekas Mihály Gyakorló Általános Iskola és Gimnázium 12. osztályos tanulója (tanárai Erdős Gábor és Dobos Sándor).

Dicséretben részesülnek két feladat teljes vagy lényegében teljes megoldásáért

Chrobák Gergő, a Debreceni Fazekas Mihály Gimnázium 11. osztályos tanulója (tanárai Gaál Istvánné és Balázs Tivadar),

Csonka Illés, a pécsi Ciszterci Rend Nagy Lajos Gimnázium 11. osztályos tanulója (tanára Baráti Ákos),

Czanik Pál, a Budapesti Fazekas Mihály Gyakorló Általános Iskola és Gimnázium 10. osztályos tanulója (tanárai Lenger Dániel és Kocsis Szilveszter),

Fleiner Zsigmond, a Budapesti Fazekas Mihály Gyakorló Általános Iskola és Gimnázium érettségizett tanulója (tanárai Hujter Bálint és Gyenes Zoltán),

Fülöp Csilla, a Szegedi Radnóti Miklós Kísérleti Gimnázium 12. osztályos tanulója (tanárai Schultz János és Mike János),

Molnár-Szabó Vilmos, a Budapesti Fazekas Mihály Gyakorló Általános Iskola és Gimnázium 12. osztályos tanulója (tanárai Dobos Sándor, Ádám Réka, Fazakas Tünde és Fey Dávid),

Móricz Benjamin, a Budapesti Fazekas Mihály Gyakorló Általános Iskola és Gimnázium 12. osztályos tanulója (tanárai Ádám Réka, Dobos Sándor, Fazakas Tünde és Szűcs Gábor),

Seres-Szabó Márton, a Budapesti Fazekas Mihály Gyakorló Általános Iskola és Gimnázium 12. osztályos tanulója (tanárai Dobos Sándor, Fazakas Tünde és Hujter Bálint),

Simon László Bence, a Budapesti Fazekas Mihály Gyakorló Általános Iskola és Gimnázium 11. osztályos tanulója (tanárai Gyenes Zoltán, Kiss Géza, Hujter Bálint, Surányi László, Mazug Péter és Sokvári Olivér).

A feladatok megoldásai megjelentek a KöMaL februári számában.

A feladatsor és a megoldások a Bolyai Társulat honlapjáról letölthetők:

https://www.bolyai.hu/versenyek-kurschak-jozsef-matematikai-tanuloverseny/

https://www.bolyai.hu/files/Kurschak_2022_feladatok.pdf

https://www.bolyai.hu/files/Kurschak_2022_elozetes_megoldasok.pdf

A 2022. évi Schweitzer Miklós Matematikai Emlékversenyről

A Bolyai János Matematikai Társulat 2022. október 28. és 2022. november 7. között rendezte meg a Schweitzer Miklós Matematikai Emlékversenyt. A versenyen középiskolai tanulók, egyetemi és főiskolai hallgatók, továbbá azok vehettek részt, akik egyetemi vagy főiskolai tanulmányaikat 2022-ben fejezték be.

A verseny lebonyolítására a Társulat a következő bizottságot kérte fel: Keleti Tamás (elnök), Ágoston Tamás (titkár), Elekes Márton, Harangi Viktor, Károlyi Gyula, Maga Balázs, Nagy János, Pach Péter Pál, Pálvölgyi Dömötör, Ráth Balázs, Tardos Gábor, Terpai Tamás, Weiner Mihály, Zábrádi Gergely.

A bizottság október 18-i ülésén kiválasztotta a 10 kitűzendő feladatot. A bizottság köszönetét fejezi ki mindazoknak, akik feladatot javasoltak a versenyre. A kitűzött feladatokat javasolták: 1. Szabó Péter, 2. Garamvölgyi Dániel, 3. Buczolich Zoltán, 4. Ruzsa Imre, 5. Keleti Tamás és Pálvölgyi Dömötör, 6. Szabó Csaba és Zábrádi Gergely, 7. Pach János és Tardos Gábor, 8. Maga Balázs, 9. Laczkovich Miklós, 10. Balka Richárd, Elekes Márton és Kiss Viktor.

A verseny eredményes volt; 17 versenyző összesen 73 megoldást nyújtott be. A versenybizottság november 28-i ülésén a következő díjakat ítélte oda:

Egyetlen versenyző oldotta meg lényegében mind a tíz feladatot.

Ennek alapján I. díjban és 200.000 Ft pénzjutalomban részesült Borbényi Márton, az ELTE idén végzett, matematikus mesterszakos hallgatója.

Borbényi Márton hibátlanul megoldotta az 1., 2., 4., 6., 7., 8., 9., 10., illetve apró pontatlanságoktól eltekintve a 3. és 5. feladatot. A bizottság szeretné kiemelni, hogy a 7. feladatra egyedül ő adott be teljes megoldást.

Egy versenyző oldott meg lényegében nyolc feladatot (1., 2., 3., 4., 5., 8., 9., 10.), valamint ért el fontos részeredményeket a 6. feladatban. Ennek alapján

II. díjban és 100.000 Ft pénzjutalomban részesült Kocsis Anett, az ELTE harmadéves, matematika alapszakos hallgatója. A bizottság szeretné kiemelni, hogy a 10. feladatra kifejezetten elegáns megoldást adott.

Két versenyző oldott meg lényegében hat feladatot és ért el további fontos részeredményeket. Ennek alapján

III. díjban és egyenként 70.000 Ft pénzjutalomban részesült Imolay András, az ELTE másodéves, matematika mesterszakos hallgatója, és Kovács Benedek, az ELTE idén végzett, matematika mesterszakos hallgatója.

Imolay András megoldotta az 1., 2., 3., 4., 5. és 9., feladatot, valamint fontos részeredményeket ért el a 6., 7. és 8. feladatban.

Kovács Benedek megoldotta az 1., 2., 4., 5., 6., apró pontatlanságoktól eltekintve a 3. feladatot, valamint a legnehezebbnek bizonyult 7. feladatban a megoldáshoz vezető kulcsfontosságú eredményt ért el.

Egy versenyző oldott meg négy feladatot (1., 4., 5., illetve lényegében a 9. feladatot), valamint ért el jelentős részeredményeket a 2. feladatban. Ennek alapján

első dicséretben és 40.000 Ft pénzjutalomban részesült Tóth Péter, a Debreceni Egyetem idén végzett, matematika mesterszakos hallgatója.

Egy versenyző oldott meg három feladatot (1., 2. és 4. feladatot), továbbá ért el értékes részeredményeket a 6. feladatban. Ennek alapján

második dicséretben és 20.000 Ft pénzjutalomban részesült Füredi Erik, az ELTE másodéves, matematika alapszakos hallgatója.

További három versenyző oldott meg teljesen két feladatot és ért el fontos részeredményeket legalább egy másik feladatban. Ennek alapján

elismerő oklevelet kapott Hegedűs Dániel, az ELTE másodéves, matematika alapszakos hallgatója, Márton Dávid, a Szegedi Tudományegyetem idén végzett, matematika mesterszakos hallgatója, és Várkonyi Zsombor, az ELTE másodéves, matematika alapszakos hallgatója.

Hegedűs Dániel megoldotta az 1. és 2. feladatot, valamint fontos részeredményeket ért el a 4. feladatban.

Márton Dávid és Várkonyi Zsombor megoldotta az 1. és 4. feladatot, valamint fontos részeredményeket ért el a 2. feladatban.

Az elsőéves alapszakos hallgatók közül az 1. feladat teljes és az 5. feladat lényegében teljes megoldásával legjobban szerepelt, és ennek alapján

a legjobb elsőévesnek járó oklevelet Kökényesi Márk, az ELTE hallgatója kapta.

A 2022. évi verseny feladatai:

1. Azt mondjuk, hogy egy 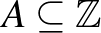$A\subseteq\mathbb{Z}$ halmaz szabálytalan, ha tetszőleges 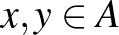$x,y\in A$ különböző elemeire nincs 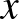$x$ -től és 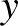$y$ -tól különböző 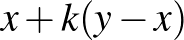$x+k(y-x)$ alakú eleme (ahol 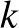$k$ egész). Létezik-e végtelen szabálytalan halmaz?

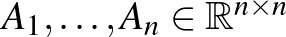2. Legyen $n$ pozitív egész. Tegyük fel, hogy az $A_1,\ldots,A_n\in\mathbb{R}^{n\times n}$ mátrixok összege az egységmátrix, de 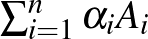$\sum_{i=1}^n \alpha_i A_i$ szinguláris minden olyan esetben, amikor az 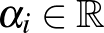$\alpha_i\in\mathbb{R}$ együtthatók közül legalább egy nulla.

a) Mutassuk meg, hogy 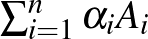$\sum_{i=1}^n \alpha_i A_i$ nemszinguláris, ha 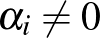$\alpha_i \neq 0$ minden 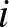$i$ -re. b) Lássuk be, hogy ha az 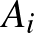$A_i$ mátrixok szimmetrikusak, akkor mindegyikük rangja $1$ .

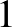3. Legyen 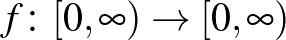$f\colon[0,\infty)\to[0,\infty)$ olyan függvény, amely szomszédos egészek között lineáris, és 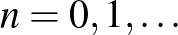$n=0,1,\ldots$ esetén

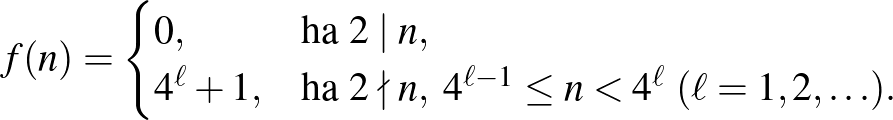
$\displaystyle f(n)=\begin{cases}0,&\text{ha }2\mid n,\\ 4^{\ell}+1,&\text{ha } 2\nmid n,\ 4^{\ell-1}\leq n<4^\ell\ (\ell=1,2,\ldots).\end{cases}$

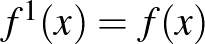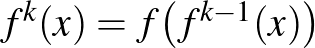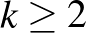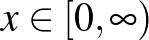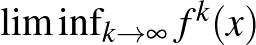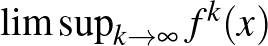Legyen $f^1(x)=f(x)$ , és $f^k(x)=f\bigl(f^{k-1}(x)\bigr)$ minden $k\geq 2$ egészre. Határozzuk meg Lebesgue majdnem minden $x\in[0,\infty)$ -re a $\liminf_{k\to\infty}f^k(x)$ és $\limsup_{k\to\infty}f^k(x)$ értékét.

4. Minden 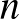$n$ -edfokú, egész együtthatós 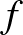$f$ polinomra tekintsük az

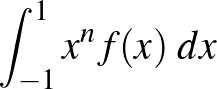
$\displaystyle \int_{-1}^1 x^n f(x) \;dx$

integrált. Jelölje 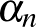$\alpha_n$ azt a legkisebb pozitív valós számot, amit ilyen integrál adhat. Határozzuk meg a

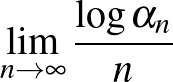
$\displaystyle \lim_{n\to\infty}\frac{\log\alpha_n}{n}$

határértéket.

5. Ki lehet-e választani a sík minden egyeneséről egy-egy nem elfajuló szakaszt úgy, hogy bármely két kiválasztott szakasz diszjunkt legyen?

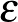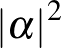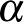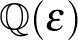6. Legyen $\varepsilon$ egy primitív hetedik egységgyök. Mely egész számok állnak elő $\left\vert\alpha\right\vert^2$ alakban, ahol $\alpha$ a $\mathbb{Q}(\varepsilon)$ hetedik körosztási test egy eleme?

7. Egy szabályos 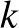$k$ -szög csúcsaiba pontszerű bábukat állítunk, majd ezekkel lépegetünk. Egy lépésben egy bábu átugrik egy másikat, azaz az új helye a pillanatnyi helyének tükörképe lesz egy másik bábu pillanatnyi helyére. Milyen 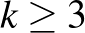$k\geq 3$ egész esetén lehet ilyen lépések sorozatával elérni, hogy a bábuk egy, az eredetitől eltérő méretű szabályos 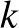$k$ -szög csúcsait alkossák?

8. Igazoljuk, hogy az 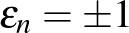$\varepsilon_n=\pm 1$ előjelek megválaszthatóak úgy, hogy az

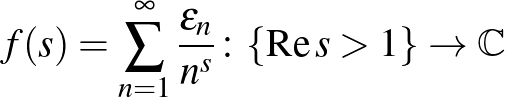
$\displaystyle f(s)=\sum_{n=1}^{\infty}\frac{\epsilon_n}{n^s}\colon\{\operatorname{Re}s>1\}\to\mathbb{C}$

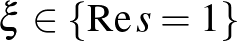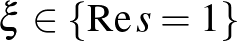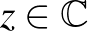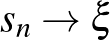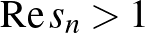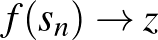függvény minden $\xi\in\{\operatorname{Re}s=1\}$ pontban minden komplex értékhez torlódik (azaz minden $\xi\in\{\operatorname{Re}s=1\}$ -hez és $z\in\mathbb{C}$ -hez létezik olyan $s_n\to\xi$ , $\operatorname{Re}s_n > 1$ sorozat, amelyre $f(s_n)\to z$ ).

9. A síkvektorok az összeadásra nézve csoportot alkotnak. Mutassuk meg, hogy ennek a csoportnak minden olyan 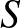$S$ halmaz generátorrendszere, amely tartalmazza egy körív pozitív lineáris mértékű Borel részhalmazát.

10. Létezik-e 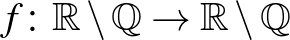$f\colon\mathbb{R}\setminus\mathbb{Q}\to\mathbb{R}\setminus\mathbb{Q}$ folytonos függvény, amelyre minden irracionális szám ősképének pozitív a Hausdorff-dimenziója?

A feladatsor és a megoldások a Bolyai Társulat honlapjáról letölthetők:

https://www.bolyai.hu/versenyek-schweitzer-miklos-emlekverseny/

https://www.bolyai.hu/files/Schweitzer%202022_feladatsor.pdf

https://www.bolyai.hu/files/Schweitzer_2022_modositott_elozetes_megoldasok.pdf

A Farkas Gyula díjakat és a Schweitzer versenydíjakat a Morgan Stanley Magyarország Elemző Kft. és a Matematika Oktatásért és Kutatásért Alapítvány támogatta.