Az Érintő Facebook-oldalán már megjelent megoldásokat a rovatszerkesztő, Róka Sándor kibővítette néhány olyan megoldással és megjegyzéssel, amit a beküldőktől kapott. Ezek újabb kérdéseket, pontosításokat vagy éppen általánosításokat, számítógépes megközelítéseket mutatnak be. Érdemes áttekinteni a különböző meggondolásokat!
22. Igaz-e, hogy tetszőleges a és b pozitív egészekhez van olyan c pozitív egész szám, amelyre 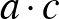 négyzetszám,
négyzetszám, 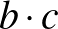 köbszám?
köbszám?
A válasz: Igaz.
Megoldás. Legyen 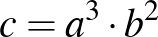 . Ekkor
. Ekkor 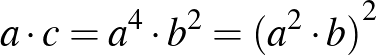 és
és 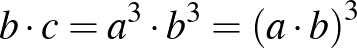 .
.
Makay Géza megoldása: Legyenek  ,
,  ,
,  ,
, 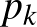 az
az 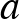 és
és 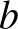 számok prímfelbontásában szereplő prímek, legyen
számok prímfelbontásában szereplő prímek, legyen
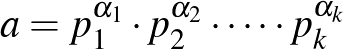
és 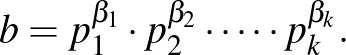
Olyan  számot keresünk, amelyet ugyanezen prímtényezőkkel fel lehet írni: felesleges újabb prímet belekeverni a dologba, de előfordulhat, hogy néhány prím nem szerepel majd a
számot keresünk, amelyet ugyanezen prímtényezőkkel fel lehet írni: felesleges újabb prímet belekeverni a dologba, de előfordulhat, hogy néhány prím nem szerepel majd a 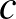 felbontásában. Ha
felbontásában. Ha
akkor a feltételek szerint 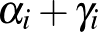 osztható 2-vel és
osztható 2-vel és 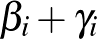 osztható 3-mal minden
osztható 3-mal minden 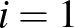 ,
, 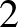 ,
, 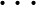 ,
, 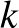 esetén. Ez könnyen elérhető, az alábbi táblázatban
esetén. Ez könnyen elérhető, az alábbi táblázatban 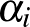 2-vel és
2-vel és 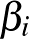 3-mal való osztási maradéka alapján megadhatjuk a
3-mal való osztási maradéka alapján megadhatjuk a 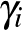 -t (vagy annak 6-tal való osztási maradékát), ami kielégíti a fenti feltételt:
-t (vagy annak 6-tal való osztási maradékát), ami kielégíti a fenti feltételt:
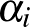 |
0 | 0 | 0 | 1 | 1 | 1 |
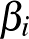 |
0 | 1 | 2 | 0 | 1 | 2 |
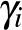 |
0 | 2 | 4 | 3 | 5 | 1 |
Megjegyzés. Diofantoszi egyenletrendszer-megoldással nemcsak négyzetszámra és köbszámra bizonyítható hasonlóan a feladat, hanem bármely két relatív prím pozitív kitevő esetére.
23. Hányféle módon lehet szétosztani 17 golyót néhány egymás után sorakozó edénybe úgy, hogy mindegyikbe legalább annyi golyót teszünk, mint amennyi az előző edényekbe összesen került? (Így például 6 golyó szétosztása eszerint a feltétel szerint 6-féleképp történhet: 1-1-4, 1-2-3, 1-5, 2-4, 3-3 és 6.)
A válasz: 36.
Megoldás. Vizsgáljuk az általános kérdést, ha 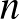 db golyót osztunk szét. A szétosztások számát jelölje
db golyót osztunk szét. A szétosztások számát jelölje 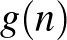 .
.
6 golyó szétosztása 6-féleképpen történhet: 1-1-4, 1-2-3, 1-5, 2-4, 3-3 és 6.
7 golyó szétosztása is 6-féleképpen történhet: 1-1-5, 1-2-4, 1-6, 2-5, 3-4 és 7.
Ha 6 golyó egy-egy szétosztásánál az utolsó edénybe 1-gyel több golyót teszünk, megkapjuk 7 golyó egy alkalmas szétosztását.
A lehetőségek száma azonos, hiszen 7 golyó esetén az utolsó edénybe legalább 4 golyó, az előző edényekbe legfeljebb 3 golyó kerül, míg 6 golyó szétosztásánál az utolsó edénybe legalább 3, az előző edényekbe legfeljebb 3 golyót teszünk.
Hasonló meggondolással látható be általánosan is: 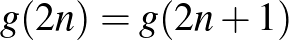 . 8 golyó szétosztása pedig 10-féleképpen történhet: 1-1-2-4, 1-1-6, 1-2-5, 1-3-4, 1-7, 2-2-4, 2-6, 3-5, 4-4 és 8.
. 8 golyó szétosztása pedig 10-féleképpen történhet: 1-1-2-4, 1-1-6, 1-2-5, 1-3-4, 1-7, 2-2-4, 2-6, 3-5, 4-4 és 8.
Felsorolás nélkül is megkaphatjuk, hogy hányféleképpen lehet 8 golyót szétosztani. Az utolsó edénybe vagy 4, vagy legalább 5 golyó kerül.
Ha 4 golyó kerül az utolsó edénybe, akkor az előtte levő edényekbe a többi 4 golyót 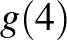 -féleképpen tudjuk szétrakni.
-féleképpen tudjuk szétrakni.
Ha az utolsó edénybe legalább 5 golyó kerül, abból 1-et félretéve, azokat a szétosztásokat kapjuk, mint 7 golyó esetén.
Hasonló meggondolással látható be általánosan is: 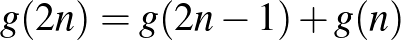 .
.
A 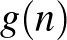 sorozat első két tagja 1 és 2, innen a
sorozat első két tagja 1 és 2, innen a 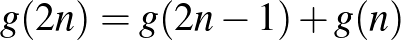 és a
és a 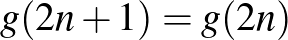 összefüggésekkel rekurzív módon számíthatjuk ki a sorozat többi tagját: 1, 2, 2, 4, 4, 6, 6, 10, 10, 14, 14, 20, 20, 26, 26, 36, 36, így
összefüggésekkel rekurzív módon számíthatjuk ki a sorozat többi tagját: 1, 2, 2, 4, 4, 6, 6, 10, 10, 14, 14, 20, 20, 26, 26, 36, 36, így 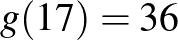 .
.
Turchányi Gyula (Belzebub) megoldása:
Megjegyzés: A feladatot a zárójelben szereplő példa egyértelműsíti (tehát nem lehetnek üresen hagyott edények).
Ha egy kicsit fordítva gondolkodunk, először azt döntsük el, hogy az utolsó edénybe mennyit teszünk. Az aktuális golyószámnak legalább a felét az utolsó edénybe kell tenni. Utána a megmaradt golyóknak (ha még van) legalább a felét az utolsó előtti edénybe, és így tovább.
A következő módokon lehet a feladat szabálya szerint a golyókat elosztani – akár kézzel is könnyű előállítani, a konstrukció közben jobbról balra haladva, a feladat példájában használt jelölést alkalmazva:
17
1-16
2-15
1-1-15
3-14
1-2-14
4-13
1-3-13
2-2-13
1-1-2-13
5-12
1-4-12
2-3-12
1-1-3-12
6-11
1-5-11
2-4-11
1-1-4-11
3-3-11
1-2-3-11
7-10
1-6-10
2-5-10
1-1-5-10
3-4-10
1-2-4-10
8-9
1-7-9
2-6-9
1-1-6-9
3-5-9
1-2-5-9
4-4-9
1-3-4-9
2-2-4-9
1-1-2-4-9.
Ha nem vagyunk kíváncsiak az összes megoldásra, csak arra, hogy összesen hány megoldás létezik, akkor egyszerűbben is számolhatunk.
Jelölje 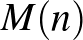 az
az 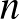 golyó esetén fennálló megoldások számát
golyó esetén fennálló megoldások számát 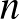 golyóra, akkor ezt a fordított gondolkodást követve az alábbi képleteket kapjuk, ha bevezetjük az
golyóra, akkor ezt a fordított gondolkodást követve az alábbi képleteket kapjuk, ha bevezetjük az 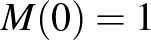 értéket is (mondhatjuk, hogy 0 golyót csak egyféleképpen helyezhetünk el).
értéket is (mondhatjuk, hogy 0 golyót csak egyféleképpen helyezhetünk el).
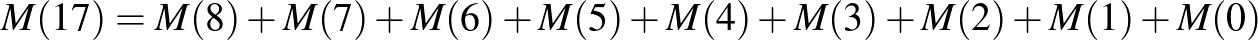
(kirakunk 9-et az utolsó edénybe, az előtte levőkbe 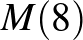 féle módon rakjuk be a megmaradt 8 golyót, vagy kirakunk 10-et az utolsó edénybe, az előtte levőkbe
féle módon rakjuk be a megmaradt 8 golyót, vagy kirakunk 10-et az utolsó edénybe, az előtte levőkbe 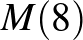 -féle módon rakjuk be a megmaradt 7 golyót, és így tovább, az utolsó edénybe rakjuk az összeset). Hasonlóan folytatva
-féle módon rakjuk be a megmaradt 7 golyót, és így tovább, az utolsó edénybe rakjuk az összeset). Hasonlóan folytatva
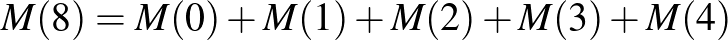 ,
,
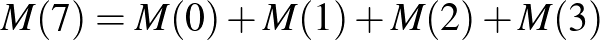 ,
,
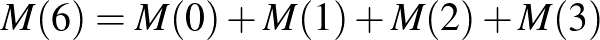 ,
,
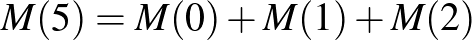 ,
,
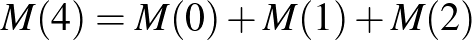 ,
,
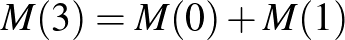 ,
,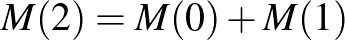 ,
,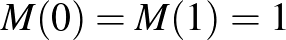 , nyilván
, nyilván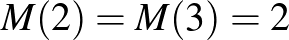 , számolva
, számolva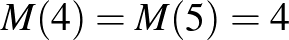 , számolva
, számolva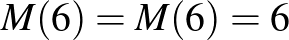 , számolva
, számolva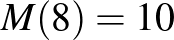 , számolva
, számolva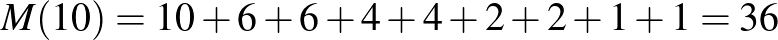 .
.
A fenti sorozat egyébként ismert: https://oeis.org/A018819 (Az OEIS egész számok sorozatainak online enciklopédiája.)
Ezen keresztül megtaláltam az egymást nem összelapító dobozok problémáját, amely azonos a feladattal:
https://citeseerx.ist.psu.edu/document?repid=rep1&type=pdf&doi=431e13433764bacfc36fc81a8740047eab909ae7.
Gaizer Tamás megoldása:
Tetszőleges 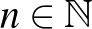 -re jelöljük
-re jelöljük 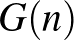 -nel a feltételeknek megfelelő szétosztások számát.
-nel a feltételeknek megfelelő szétosztások számát.
Egyrészt világos, hogy 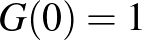 (hiszen 0 darab golyót egyetlen módon oszthatunk szét: egyetlen edénybe se teszünk semmit), másrészt az is könnyen látható, hogy
(hiszen 0 darab golyót egyetlen módon oszthatunk szét: egyetlen edénybe se teszünk semmit), másrészt az is könnyen látható, hogy 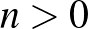 -ra a szétosztások számát az alábbi rekurzióval határozhatjuk meg:
-ra a szétosztások számát az alábbi rekurzióval határozhatjuk meg:
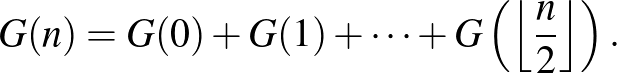
A képlet magyarázata egyszerű: jelölje 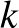 az utolsó edénybe kerülő golyók számát. Mivel ennek nagyobbnak kell lennie a többi edénybe rakott golyók összegénél,
az utolsó edénybe kerülő golyók számát. Mivel ennek nagyobbnak kell lennie a többi edénybe rakott golyók összegénél, 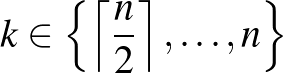 . Nyilvánvaló, hogy tetszőleges
. Nyilvánvaló, hogy tetszőleges 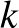 -ra a maradék golyókat
-ra a maradék golyókat 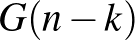 féleképpen oszthatjuk szét, ezért ha
féleképpen oszthatjuk szét, ezért ha 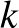 befutja a
befutja a 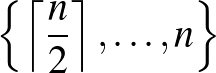 halmazt, akkor
halmazt, akkor 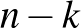 lehetséges értékei éppen a
lehetséges értékei éppen a 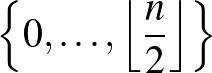 halmaz elemei lesznek.
halmaz elemei lesznek.
Mivel 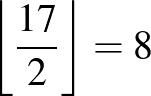 , a fentiek alapján a feladat megoldásához a
, a fentiek alapján a feladat megoldásához a 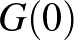 ,
, 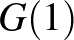 ,
,  ,
, 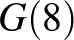 értékeket kell meghatároznunk, ezt az alábbi táblázatban tesszük meg (a számolást valamennyivel gyorsítja, ha kihasználjuk, hogy tetszőleges
értékeket kell meghatároznunk, ezt az alábbi táblázatban tesszük meg (a számolást valamennyivel gyorsítja, ha kihasználjuk, hogy tetszőleges 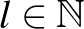 -re
-re 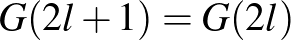 ):
):
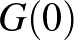 |
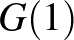 |
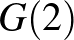 |
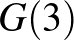 |
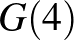 |
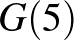 |
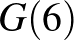 |
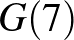 |
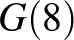 |
| 1 | 1 | 2 | 2 | 4 | 4 | 6 | 6 | 10 |
Az előzőek szerint 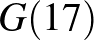 a táblázat második sorában szereplő számok összege lesz, azaz
a táblázat második sorában szereplő számok összege lesz, azaz 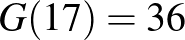 , ennyi módon oszthatjuk szét a golyókat.
, ennyi módon oszthatjuk szét a golyókat.
24. Zsófi bábukat rak egy üres sakktáblára. Akkor helyezhet el egy bábut egy üres mezőre, ha annak van legalább három üres oldalszomszédja. Legfeljebb hány bábut helyezhet a táblára Zsófi?
A válasz: 36.
Megoldás. A tábla mezőit jelöljük egy-egy ponttal, és ha két mező szomszédos, akkor a két pontot kössük össze szakasszal. Így a 64 pont között 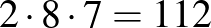 szakaszt rajzolunk.
szakaszt rajzolunk.

Ha elfoglalunk egy mezőt, akkor szüntessük meg az innen induló szakaszokat. Ilyenkor legalább három szakaszt törlünk. Egy újabb bábut csak olyan mezőre tehetünk, ahonnan legalább 3 szakasz indul.
Így a négy sarokba nem tehetünk bábut. Tekintsük a legfelső sort, ebben hét vízszintes szakasz van. Ha ezekből egy bábu elhelyezésekor eltűnik egy szakasz, akkor egy másik, a közvetlen mellette levő szakasz is eltűnik, azaz a felső sorból csak kettesével tudunk szakaszt törölni, tehát a hét szakaszból egy biztosan megmarad. Ugyanez igaz a legalsó sorra, valamint a két szélső oszlop függőleges szakaszaira, azaz a széleken megmarad egy-egy szakasz.
A 112 szakaszból legfeljebb 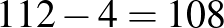 szakaszt törölhetünk. Ezért legfeljebb 36 bábut tehetünk fel, hiszen 37 bábu elhelyezésével legalább
szakaszt törölhetünk. Ezért legfeljebb 36 bábut tehetünk fel, hiszen 37 bábu elhelyezésével legalább 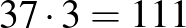 szakaszt szüntetnénk meg.
szakaszt szüntetnénk meg.
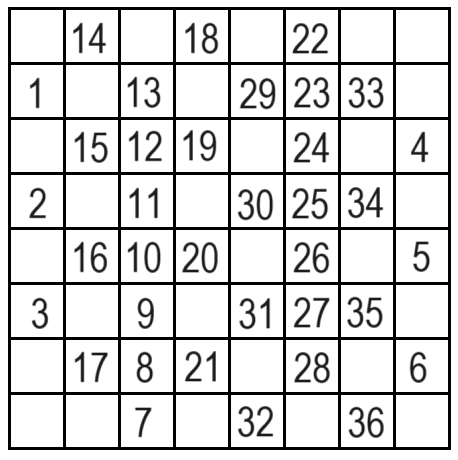
Elhelyezhetünk 36 bábut, ezt látjuk az ábrán. A táblán a számok mutatják a felhelyezés sorrendjét.
Megjegyzés: Sokan észrevették, hogy a feladat rokonságban van 17. feladattal, az ottani bizonyítás itt is működik.
25. Az 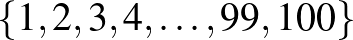 halmaz legalább kételemű részhalmazát nevezzük átlagosnak, ha a részhalmazban lévő számok átlaga (számtani közepe) egész szám. Az átlagos részhalmazok száma páros vagy páratlan?
halmaz legalább kételemű részhalmazát nevezzük átlagosnak, ha a részhalmazban lévő számok átlaga (számtani közepe) egész szám. Az átlagos részhalmazok száma páros vagy páratlan?
A válasz: Páros.
Megoldás. Az átlagos részhalmazok párokba rendezhetők.
Az  átlagos részhalmazban lévő számok átlaga legyen
átlagos részhalmazban lévő számok átlaga legyen  . Két eset lehet.
. Két eset lehet.
Ha  , akkor
, akkor 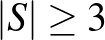 , mert kételemű halmaz esetén ha az egyik elem
, mert kételemű halmaz esetén ha az egyik elem 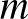 , nem lehet az átlag is
, nem lehet az átlag is 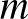 . Legyen az
. Legyen az 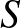 halmaz párja:
halmaz párja: 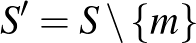 . Mivel
. Mivel 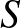 elemeinek átlaga
elemeinek átlaga 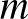 volt, ezért az
volt, ezért az 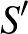 halmaz elemeinek átlaga is
halmaz elemeinek átlaga is 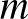 lesz (ez könnyen látható), és teljesül, hogy
lesz (ez könnyen látható), és teljesül, hogy 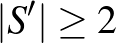 , így
, így 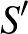 egy átlagos részhalmaz.
egy átlagos részhalmaz.
Ha pedig 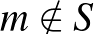 , akkor az
, akkor az 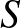 halmaz párja:
halmaz párja: 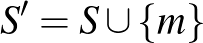 . Az
. Az 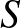 elemeinek átlaga
elemeinek átlaga 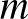 volt, ezért az
volt, ezért az 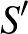 halmaz elemeinek átlaga is
halmaz elemeinek átlaga is 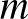 lesz.
lesz.
A két párbaállítás ugyanaz, csak a szerepek cserélődnek.
Dombi Péter szép megfogalmazásában a megoldás:
Az átlagos halmazok száma mindig páros. Vegyük azt a megfeleltetést, ami az 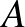 halmazhoz hozzáveszi a
halmazhoz hozzáveszi a 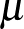 átlagot, ha az nincs benne a halmazban, illetve törli a
átlagot, ha az nincs benne a halmazban, illetve törli a 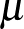 átlagelemet a halmazból, ha az benne volt. Ez egy fixpontmentes leképezés, ami párba állítja az átlagos halmazokat, tehát ezek száma páros.
átlagelemet a halmazból, ha az benne volt. Ez egy fixpontmentes leképezés, ami párba állítja az átlagos halmazokat, tehát ezek száma páros.
Találhatunk másik megfeleltetést is, ha az ![$A=\{a_1,\dots,a_k\}\subset [1,100]$](/images/stories/latexuj/2024-06/2024-06-hettusa4megoldasok/img91.png) halmazhoz az
halmazhoz az 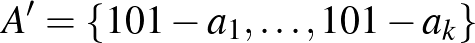 halmazt rendelnénk, akkor az előbbihez hasonlóan ez is fixpontmentes – kölcsönösen egyértelmű – involúció, ez viszont kihasználja, hogy 101 páratlan, tehát csak páros elemszámú halmazokra működik.
halmazt rendelnénk, akkor az előbbihez hasonlóan ez is fixpontmentes – kölcsönösen egyértelmű – involúció, ez viszont kihasználja, hogy 101 páratlan, tehát csak páros elemszámú halmazokra működik.
Makay Géza: Erre egy rövidebb (30 soros) programot lehet írni, amivel 20 elemű halmazokig kiszámolva az összes nem üres részhalmazt, megkapjuk, hogy azok közül hány átlagos:
1, 2, 5, 8, 15, 26, 45, 76, 135, 238, 425, 768, 1399, 2570, 4761, 8856, 16567, 31138, 58733, 111164.
Természetesen ezt is megtaláltam az OEIS-en, ráadásul pontosan ugyanezzel a definícióval: A051293 (Number of nonempty subsets of 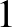 ,
, 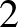 ,
, 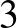 ,
, 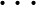 ,
, 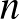 whose elements have an integer average). Nem tudom, szándékos volt-e a kitűző részéről, de a legalább kételemű átlagos részhalmazok száma nincs benne az OEIS-ben. Viszont az a fentiből könnyen kiszámolható, hiszen minden egyelemű részhalmaz természetesen átlagos is, vagyis a fenti számokból le kell vonni az elemek számát, hogy megkapjuk az eredményt:
whose elements have an integer average). Nem tudom, szándékos volt-e a kitűző részéről, de a legalább kételemű átlagos részhalmazok száma nincs benne az OEIS-ben. Viszont az a fentiből könnyen kiszámolható, hiszen minden egyelemű részhalmaz természetesen átlagos is, vagyis a fenti számokból le kell vonni az elemek számát, hogy megkapjuk az eredményt:
0, 0, 2, 4, 10, 20, 38, 68, 126, 228, 414, 756, 1386, 2556, 4746, 8840, 16550, 31120, 58714, 111144.
Itt minden szám páros, tehát várható, hogy 100-elemű halmazra is páros lesz az eredmény.
Az OEIS nem ad sem zárt, sem rekurzív képletet a fenti sorozatra, így nem nagyon van esélyünk meghatározni a százelemű halmaz esetén az átlagos halmazok konkrét számát (túl sok van belőlük), más ötlet kell.
Turchányi Gyula (Belzebub) programot írt, amely kiszámolta az átlagos részhalmazok számát:
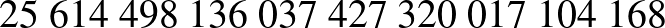 .
.(A programot kiteszi a github.com-ra.)
Keresztvölgyi József teljes indukcióval bizonyította, hogy az 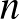 -elemű halmaz (
-elemű halmaz (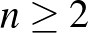 ) átlagos részhalmazainak száma páros.
) átlagos részhalmazainak száma páros.
Izsák Beatrix utalt a KöMaL-ban 2019-ben megjelent B. 5043. feladatra (amiről a kitűző már megfeledkezett): Mutassuk meg, hogy az 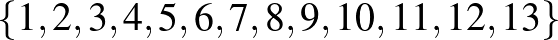 halmaznak páratlan sok olyan nemüres részhalmaza van, amelyben az elemek átlaga egész szám.
halmaznak páratlan sok olyan nemüres részhalmaza van, amelyben az elemek átlaga egész szám.
Az ott közölt megoldás segít itt is.
26. A síkon felvettünk 11 pontot úgy, hogy nincs közte három olyan, amely egy egyenesre esne, így bármely három pont egy háromszög csúcsait alkotja. Lehetséges-e, hogy a háromszögeknek legalább a fele ugyanakkora területű?
A válasz: Nem lehet.
Megoldás. Az ugyanakkora területű háromszögek száma legyen 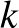 .
.
Számoljuk meg az ugyanakkora területű háromszögek oldalait, azaz háromszögenként 3 oldalt, az eredmény 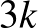 .
.
Lehetnek olyan oldalak, amelyeket többször is számoltunk. Egy 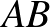 háromszögoldalt legfeljebb 4-szer számolhatunk, hiszen az ugyanakkora terület miatt a háromszög harmadik csúcsa az
háromszögoldalt legfeljebb 4-szer számolhatunk, hiszen az ugyanakkora terület miatt a háromszög harmadik csúcsa az 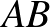 egyenes valamelyik oldalán fekvő AB-vel párhuzamos egyenesen lehet, ahol a párhuzamos egyenes és
egyenes valamelyik oldalán fekvő AB-vel párhuzamos egyenesen lehet, ahol a párhuzamos egyenes és 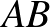 távolsága egyértelmű a terület miatt, és egy egyenesen nem lehet 3 pont.
távolsága egyértelmű a terület miatt, és egy egyenesen nem lehet 3 pont.
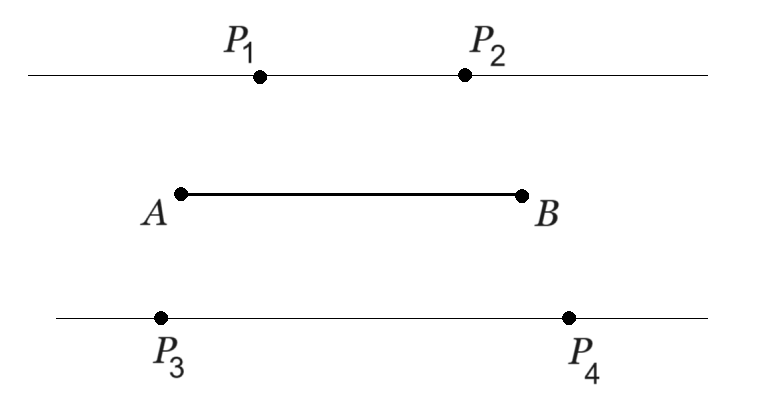
Az 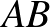 -nek választott oldal a
-nek választott oldal a 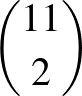 pontpár bármelyike lehet, ezért legfeljebb
pontpár bármelyike lehet, ezért legfeljebb 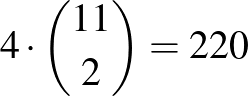 háromszögoldalt számolhattunk.
háromszögoldalt számolhattunk.
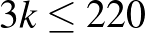 ,
, 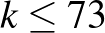 . Az ugyanakkora területű háromszögek száma legfeljebb 73.
. Az ugyanakkora területű háromszögek száma legfeljebb 73.
A 11 pont összesen 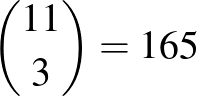 háromszöget határoz meg, és
háromszöget határoz meg, és 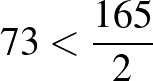 , így nem lehet a háromszögeknek legalább a fele ugyanakkora területű.
, így nem lehet a háromszögeknek legalább a fele ugyanakkora területű.
Turchányi Gyula (Belzebub) megjegyzi, hogy a szabályos hatszög jó példa arra, hogy 6 pont esetén még teljesül a feladat kritériuma.
27. Egy kisvárosban 7 buszmegálló van, és néhány autóbuszjárat. Mindegyik buszjáratnak 3 buszmegállója van, és két buszjáratnak legfeljebb egy közös megállója lehet. Legfeljebb hány buszjárat lehet ebben a városban?
A válasz: 7.
Megoldás. Az a feladat, hogy az 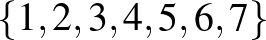 halmaznak válasszuk ki a lehető legtöbb 3-elemű részhalmazát úgy, hogy bármely két részhalmaznak legfeljebb egy közös eleme legyen.
halmaznak válasszuk ki a lehető legtöbb 3-elemű részhalmazát úgy, hogy bármely két részhalmaznak legfeljebb egy közös eleme legyen.
Az 1, 2, 3, 4, 5, 6, 7 számok bármelyike legfeljebb három részhalmazban lehet. Hiszen ha négy részhalmaznak is eleme lenne, akkor felsorolva ennek a négy 3-elemű részhalmaznak további két-két elemét, azok mind különbözők a feltétel miatt, így a közös elemmel együtt összesen 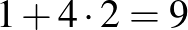 elemet kapunk, miközben az alaphalmaz 7-elemű.
elemet kapunk, miközben az alaphalmaz 7-elemű.
Ha a kiválasztott 3-elemű halmazok száma  , akkor ezek elemeit felsorolva
, akkor ezek elemeit felsorolva  elem szerepel ezen a listán. Mivel bármelyik szám legfeljebb három 3-elemű halmazban van, így
elem szerepel ezen a listán. Mivel bármelyik szám legfeljebb három 3-elemű halmazban van, így 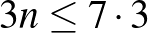 , ezért
, ezért 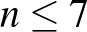 .
.
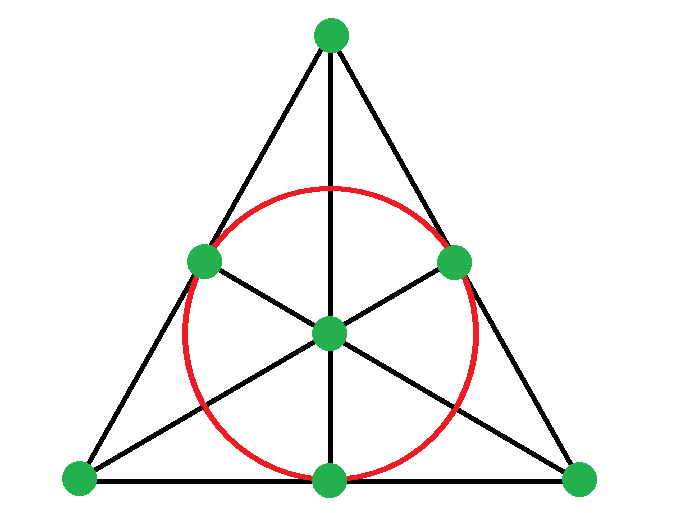
Van 7 ilyen részhalmaz, azaz 7 alkalmas buszjárat. Az ábrán a 7 pont a 7 megálló, a 7 buszjárat a háromszög 3 oldala, a háromszög 3 magasságvonala és a körformájú útvonal.
Kovach M. László elegáns megoldása:
Minden buszmegálló legfeljebb 3 járatnak lehet megállója, hiszen (járatonként) a többi 2-2 megálló különböző kell legyen. Tehát legfeljebb 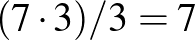 járat lehet.
járat lehet.
Azt, hogy a 7 elérhető, a híres ún. Fano-sík mutatja, lásd: https://en.wikipedia.org/wiki/Fano_plane.
Izsák Beatrix indoklása: A 7 buszmegálló 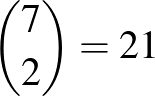 útszakaszt határoz meg. Minden buszjárat 3 ilyen szakaszból áll, és mivel minden szakaszhoz 2 megálló tartozik, ezért 1 szakasz csak 1 buszjárathoz tartozhat.
útszakaszt határoz meg. Minden buszjárat 3 ilyen szakaszból áll, és mivel minden szakaszhoz 2 megálló tartozik, ezért 1 szakasz csak 1 buszjárathoz tartozhat. 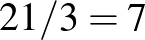 , tehát legfeljebb 7 buszjárat lehet a városban. (Ez azonban többféleképpen is lehetséges..., pl. 125, 136, 147, 234, 267, 357, 456 ahol 1-től 7-ig a számok a buszmegállókat jelölik.)
, tehát legfeljebb 7 buszjárat lehet a városban. (Ez azonban többféleképpen is lehetséges..., pl. 125, 136, 147, 234, 267, 357, 456 ahol 1-től 7-ig a számok a buszmegállókat jelölik.)
28. A hét törpe körbeüli az asztalt, és Hófehérke mindegyiknek annyi cukorkát ad, ahány hüvelyk a különbség a törpe két szomszédjának magassága között. Legfeljebb hány cukorkát oszthat szét közöttük Hófehérke, ha a törpék magassága 31, 32, 33, 34, 35, 36 és 37 hüvelyk?
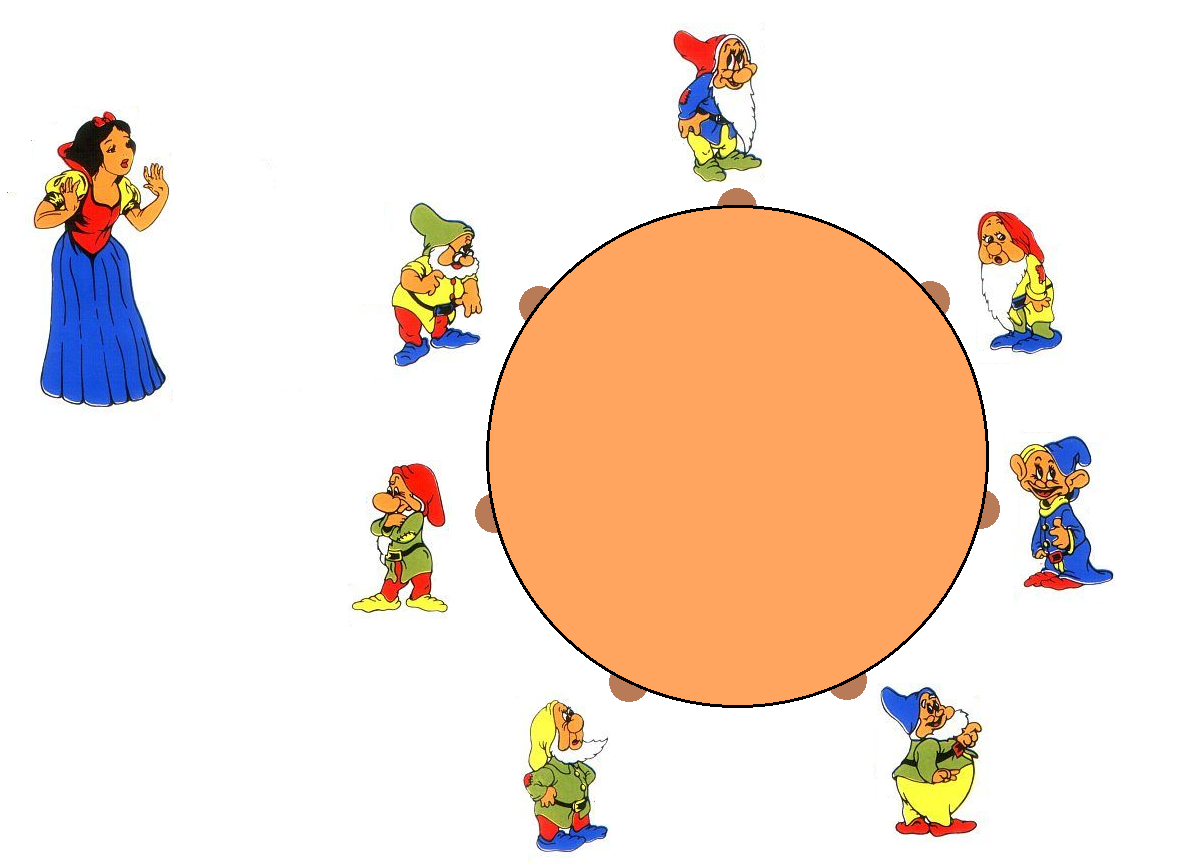
A válasz: 24.
Megoldás. A 31, 32, ..., 37 számok helyett az 1, 2, ..., 7 számokat nézzük. Ez nem változtatja meg a kiosztott cukorkák számát.
Rendezzük át a hét számot az ábra szerinti új sorrendbe. Az új helyzetben a szomszédos számok különbségeit kell figyelnünk a másodszomszédos számok különbsége helyett.
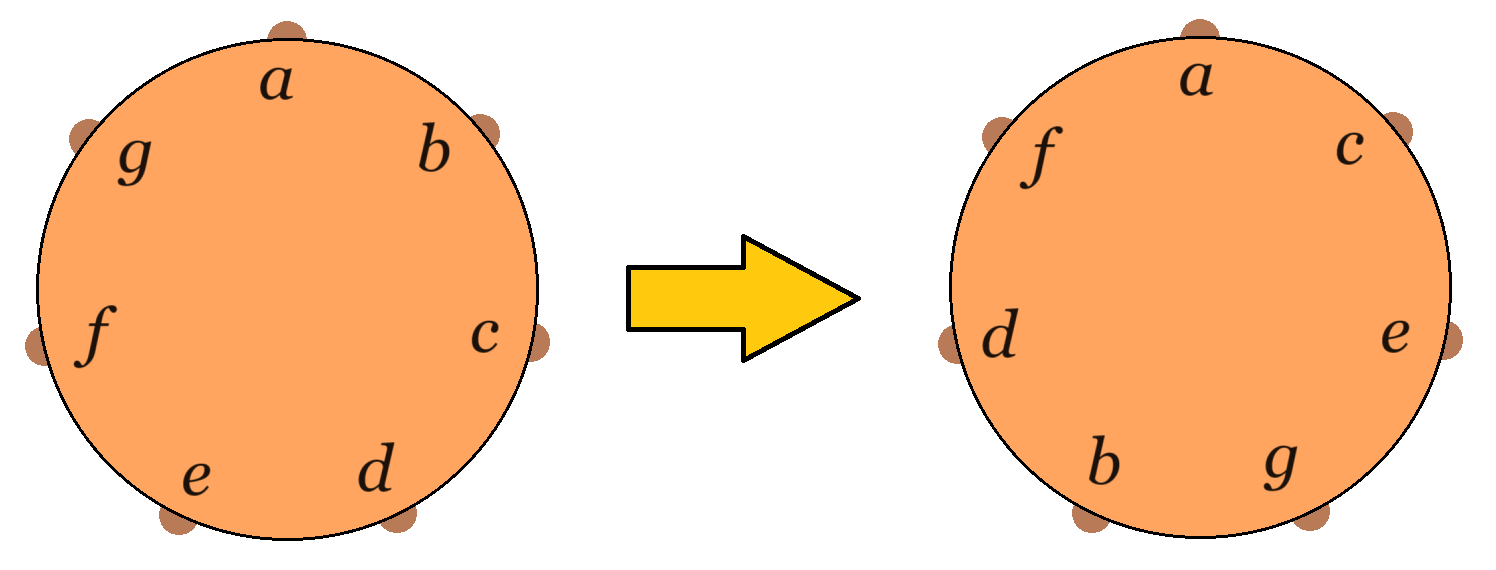
Az így módosított feladat: Egy körre felírjuk az 1, 2, 3, 4, 5, 6, 7 számokat valamilyen sorrendbe, majd kiszámoljuk a szomszédos számok közti pozitív különbséget, és a kapott hét különbséget összeadjuk. Mekkora ennek az összegnek a legnagyobb értéke?
Válasszunk egy számot, legyen ez a 4, és nézzük meg, hogyan befolyásolja a számolt összeget. Három lehetőségre figyelhetünk: a szomszédos két szám kisebb nála; vagy az egyik nagyobb, a másik kisebb; vagy azok nagyobbak.
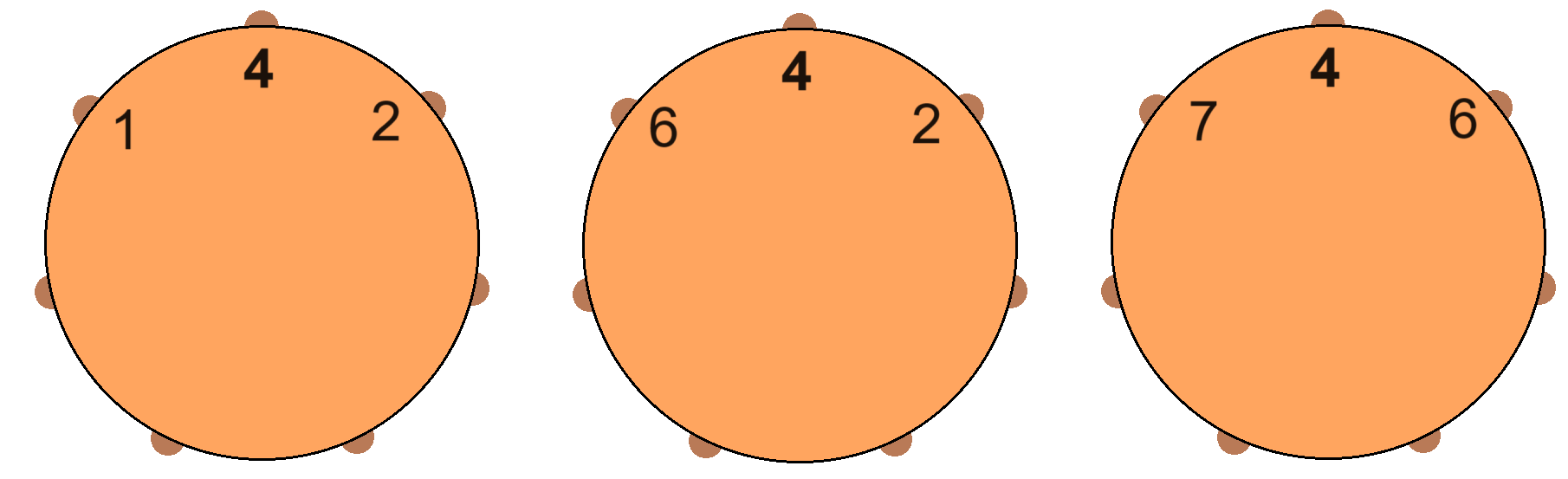
Amikor kiszámoljuk a szomszédos számok közti pozitív különbségek összegét, ebben a műveletsorban az 1, 2, ..., 7 számok mindegyike két különbségben szerepel.
Az ábrák szerinti helyzetekben a különbségek összegében a 4 összeadandóként 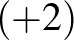 -szer, 0-szor vagy
-szer, 0-szor vagy 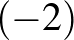 -szer szerepel.
-szer szerepel.
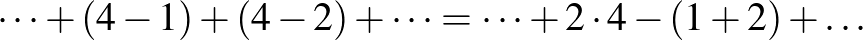 , azaz
, azaz 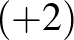 -szer;
-szer;
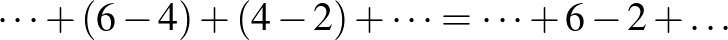 , azaz 0-szor;
, azaz 0-szor;
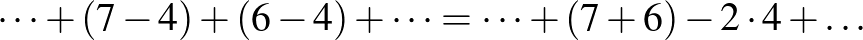 , azaz
, azaz 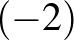 -szer.
-szer.
Ez mindegyik számra teljesül.
Ha az 1, 2, 3, 4, 5, 6, 7 számok közül valamelyik 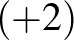 -szer szerepel, akkor ez a szám kiemelkedik, azaz nagyobb, mint a két szomszédja. Ezért nem állhat egymás mellett két kiemelkedő szám, a hét szám közül legfeljebb három szám lehet kiemelkedő. Ekkor van három olyan, alacsony szám is, amely kisebb, mint a két szomszédja. Az alacsony számok az összegben
-szer szerepel, akkor ez a szám kiemelkedik, azaz nagyobb, mint a két szomszédja. Ezért nem állhat egymás mellett két kiemelkedő szám, a hét szám közül legfeljebb három szám lehet kiemelkedő. Ekkor van három olyan, alacsony szám is, amely kisebb, mint a két szomszédja. Az alacsony számok az összegben 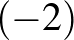 -szer szerepelnek. Amiatt, hogy az összeg értéke kevéssel csökkenjen, alacsony számoknak a kis számokat választjuk.
-szer szerepelnek. Amiatt, hogy az összeg értéke kevéssel csökkenjen, alacsony számoknak a kis számokat választjuk.
Így kaphatjuk meg a legnagyobb összeget, ha az 5, 6 és 7 számok kiemelkednek, közöttük vannak egyenként az alacsony számok, az 1, 2 és 3, míg a 4 bárhol lehet.
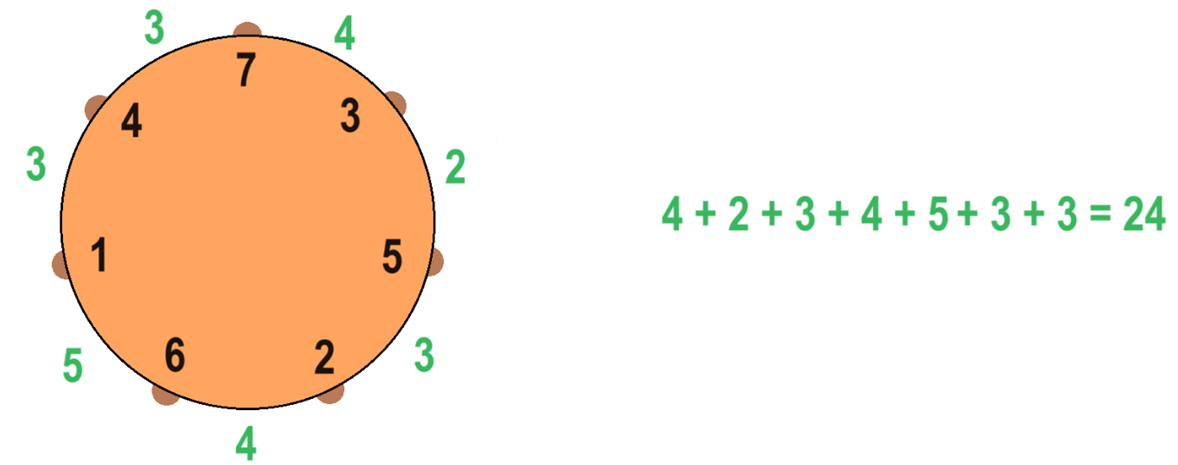
A különbségek legnagyobb összege 24.
Hófehérke legfeljebb 24 cukorkát oszthat szét a törpék között.
Róka Sándor











