Egy matematikai állítás felfedezéséhez vagy bizonyításához ma már a legtöbb matematikus nem csak papírt és ceruzát használ, sok esetben segítségül hívja a számítógépet. A számítógépes programokat milliónyi adaton lefuttatva megsejthető a válasz egy-egy híres problémára, vagy egy új tétel kérdésfelvetésére – akkor már „csak” be kell bizonyítani matematikai módszerekkel ☺.
Ez a gondolkodásmód is megjelenik Makay Géza megoldásai között, amelyek kitekintést nyújtanak túl a hivatalos mintamegoldásokon.
Makay Géza 1985-ben és '86-ban is érmet szerzett a Nemzetközi Matematikai Diákolimpián, azóta is szereti a kihívást jelentő matematikai problémákat. 1991 óta a Szegedi Tudományegyegyetem Analízis Tanszékének oktatója, hobbija a programozás. Nem csoda hát, hogy szerepel a Héttusa megoldói között, néhány feladathoz programot ír, néhány példát általánosít.
8. Igaz-e, hogy bármely pozitív páros szám előáll két olyan szám összegeként, amelyek mindegyike páratlan számjegyekből áll?
Megoldás: A rövid válasz, hogy az állítás nem igaz, például a 220 nem állítható elő így. De lássuk, hogy honnan is jön ez az ellenpélda, vizsgáljuk meg a feladatot kicsit részletesebben.
A csupa páratlan számjegyből álló számokat nevezzük ezentúl erősen páratlan számoknak. Könnyen ellenőrizhető, hogy a 20-nál kisebb pozitív páros számok előállnak két erősen páratlan szám összegeként.
Próbáljuk ki, hogyan lehetne egy nagyobb, több számjegyből álló páros számot felbontani két erősen páratlan szám összegére. Ehhez gondoljuk át a papíron való összeadás műveletét. Az összegben adott helyiértéken szereplő számjegy három másikból áll elő: a két összeadandó megfelelő helyiértékén levő számjegyéből és az esetleges átvitelből. Vagyis ha két erősen páratlan szám összegében páratlan számjegy áll, az vagy úgy lehetséges, hogy az előző helyiértéken átvitel keletkezik, vagy úgy, hogy az egyik összeadandónak már nincs azon a helyiértéken számjegye. Pozitív páros számunkból képezzünk annyi páros számot, amennyi helyiértékből az áll. Kezdjük az egyesekkel, haladjunk visszafelé. Egy helyiértékhez tartozó szám legyen ugyanaz, mint az eredetiben, ha az páros. Ha pedig az eredeti szám egyik helyiértékén páratlan szám szerepelt, ehhez a helyiértékhez tartozzon eggyel kisebb szám és az „átvitel”: az előző helyiértékhez tartozó páros számhoz adjunk hozzá 10-et. Így az eredeti számunkat felbontonthatjuk speciális alakú számok összegére, amelyekben vagy egy páros számjegy után, vagy egy 1-es és egy páros számjegy után a helyiértéknek megfelelő számú 0 van, ez pontosan megfelel a papíron való összeadás műveletének. Tekintsük példaként a 736450 számot.
| 1 | 0 | egyesek | 1 | 0 | ||||||||||||
| + | 4 | tízesek | + | 4 | 0 | |||||||||||
| + | 4 | százasok | + | 4 | 0 | 0 | ||||||||||
| + | 1 | 6 | ezresek | + | 1 | 6 | 0 | 0 | 0 | |||||||
| + | 1 | 2 | tízezresek | + | 1 | 2 | 0 | 0 | 0 | 0 | ||||||
| + | 6 | százezresek | + | 6 | 0 | 0 | 0 | 0 | 0 | |||||||
| 7 | 3 | 6 | 4 | 5 | 0 | összeg | 7 | 3 | 6 | 4 | 5 | 0 |
A ténylegesen összeadott számok a megfelelő helyiérték után csupa 0 számjegyet tartalmaznak, az azelőtti részen pedig egy 20-nál kisebb páros szám áll (ez a fenti bal oldali oszlopban jól látszik). Ez utóbbi mindig felbontható két páratlan számjegy összegére, így kaphatjuk meg például a következő felbontást:
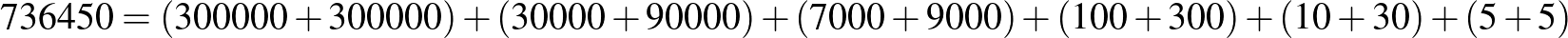 .
.
Minden zárójeles kifejezésből egy-egy tagot véve, az eredeti számot két csupa páratlan számjegyet tartalmazó szám összegére bonthatjuk:
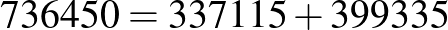 .
.
Mindig működik-e ez az eljárás? A válasz az, hogy nem: ha valamelyik fenti, 20-nál kisebb számunk a 0 lenne (ha az összegben azon a helyiértéken 0 vagy 1 áll, és az eggyel nagyobb helyiértéken páros szám van), akkor ezt a 0-t csak átvitellel tudjuk felbontani két páratlan szám összegére, és a következő helyiértéken átvitelt kapunk, pedig nem kellene. És ez az egyetlen eset, ami problémát okozhat, bár nem feltétlenül okoz, hiszen pl. 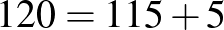 . De a 220 nem bontható fel, hiszen az átvitel miatt az utolsó két számjegyet csak úgy lehet előállítani, hogy az egyikben van egy páros számjegy a tízes helyiértéken. Igaz, az lehet 0 is (sőt, ebben a konkrét esetben annak kell lennie), az viszont azt jelenti, hogy annak a számnak nagyobb helyiértékű számjegye nem lehet, mert akkor a 0 számjegy konkrétan meg is jelenne a számban, és nem lenne erősen páratlan. Így viszont bármilyen páratlan
. De a 220 nem bontható fel, hiszen az átvitel miatt az utolsó két számjegyet csak úgy lehet előállítani, hogy az egyikben van egy páros számjegy a tízes helyiértéken. Igaz, az lehet 0 is (sőt, ebben a konkrét esetben annak kell lennie), az viszont azt jelenti, hogy annak a számnak nagyobb helyiértékű számjegye nem lehet, mert akkor a 0 számjegy konkrétan meg is jelenne a számban, és nem lenne erősen páratlan. Így viszont bármilyen páratlan  számjegyet is veszünk annak a számnak, a másik tag
számjegyet is veszünk annak a számnak, a másik tag 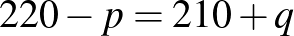 alakú, ahol
alakú, ahol 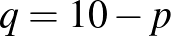 , és így abban a számban a százasok helyén mindig páros szám (2) áll.
, és így abban a számban a százasok helyén mindig páros szám (2) áll.
8.1. kérdés: Melyek azok a számok, amelyek nem bonthatók fel két erősen páratlan szám összegére?
Megoldás: Probléma akkor lehet, ha egy páros számjegyet 0 vagy 1 számjegy követ. Hogy tömörebben tudjunk fogalmazni, bevezetjük az informatikában jól ismert és mintailleszkedés vizsgálatára gyakran használt reguláris kifejezés fogalmát, persze nem a maga teljességében, mert az messze túlmutat ezen a problémán. Van is egy vicc ezzel kapcsolatban: „Egy programozónak van egy problémája. Úgy gondolja, hogy majd reguláris kifejezésekkel oldja meg. Most már két problémája van.” ☺. Ez rám nem vonatkozik, egyrészt, mert matematikus vagyok, másrészt, mert egy reguláris kifejezéseket is használó programmal ellenőriztem a dolgokat és szereztem sejtést, harmadrészt, mert most már nincs problémám, megoldottam a feladatot... ☺
Szögletes zárójelben fogjuk felsorolni egy adott helyiértéken szereplő lehetséges számjegyeket, a „.” karakter egy tetszőleges számjegyet jelölhet. A „.*” karaktersor akárhány (akár 0 darab) számjegyet helyettesíthet, míg például a „[13579]*” akárhány páratlan számjegyet jelenthet. Így a megoldás első mondatából az derül ki, hogy a „.*[02468][01].*” alakú számokkal lehet probléma, de nem biztos, hogy van. Bontsuk ezt esetekre:
1. A „.*[2468].*[2468][01].*” alakú számokkal mindenképpen baj van, mert az átvitel miatt a [01] előtti [2468] számjegy helyiértékén az egyik összeadandóban 0-nak kell lennie, így abban nagyobb helyiértékű számjegy sem lehet. Ez azt jelenti, hogy a másik összeadandóban van egy páros számjegy az első [2468] számjegy helyiértékén, így az nem erősen páratlan. Erre példa a 220 is, de hosszabb és bonyolultabb számot is könnyen mondhatunk a reguláris kifejezés mintája alapján, pl. az 54378167258 számban a 81-es rész a probléma, és mivel afelett van páros számjegy, ezért nincs felbontás. Vegyük észre, hogy az „[13579]*[2468][01].*” alakú számok felbonthatók (persze ha a „.*” rész nem illeszkedik valamelyik kizárható esetre), így már csak a „.*[0][01].*” alakú számokat kell megvizsgálnunk.
2. Ha a „.*[0][01].*” alakú számban a [0] számjegy előtt páros számjegy áll, akkor újrakezdhetjük a reguláris kifejezés illesztését az 1. ponttól. Ez azt jelenti, hogy már csak a „.*[13579][0][01].*” alakú számok lehetnek problémásak.
3. A „.*[3579][0][01].*” alakú számok sem bonthatók fel, mert az átvitel miatt a [01] előtti 0 számjegy ismét csak átvitellel bontható fel, így az az előtti páratlan számból valami nem 0 páros lesz, és az megintcsak a fennmaradó egyetlen összeadandónak lesz azon a helyiértéken a számjegye. Például a 300 ilyen alakú szám, de a 36701962 is ilyen, hiszen ott van benne a reguláris kifejezés mintája: a 701-es rész. Megmaradtak még a „.*[1][0][01].*” alakú számok, amelyeket meg kell néznünk.
4. A „.*[123456789].*[1][0][01].*” alakú számok sem jók felbontási szempontból, mert az átvitel miatt a [01] előtti 0 számjegy ugyancsak átvitellel bontható fel, így az az előtti 1-esből 0 lesz. Ez még nem is lenne baj (például 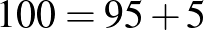 ), de ha az 1-es számjegy előtt is van még valami értékes számjegy, akkor annak valamelyik összeadandóban meg kellene jelennie, de a 100 csak úgy bontható fel, hogy a felbontásban a 100-as helyiértékeken már 0 kell legyen mindkét összeadandóban, így egyik sem tudja produkálni a magasabb helyiértéken levő számjegyet. Erre a mintára a legkisebb példa az 1100, de erre is lehetne ennél nagyobb példákat is hozni. A „[1][0][01].*” alakú számok felbonthatók (persze ismét csak akkor, ha a „.*” rész nem illeszkedik valamelyik kizárható esetre), és ezzel az összes esetet végignéztük.
), de ha az 1-es számjegy előtt is van még valami értékes számjegy, akkor annak valamelyik összeadandóban meg kellene jelennie, de a 100 csak úgy bontható fel, hogy a felbontásban a 100-as helyiértékeken már 0 kell legyen mindkét összeadandóban, így egyik sem tudja produkálni a magasabb helyiértéken levő számjegyet. Erre a mintára a legkisebb példa az 1100, de erre is lehetne ennél nagyobb példákat is hozni. A „[1][0][01].*” alakú számok felbonthatók (persze ismét csak akkor, ha a „.*” rész nem illeszkedik valamelyik kizárható esetre), és ezzel az összes esetet végignéztük.
8.2. kérdés: Egy adott szám hányféleképpen bontható fel két erősen páratlan szám összegére?
Megoldás: Már tudjuk, hogy mely számokra lesz az eredmény 0. Nézzük a többit.
Ha még egyszer meggondoljuk a papíron való összeadás műveletét, akkor kiderül, hogy csak a fenti módszerrel lehet egy páros számot erősen páratlan számokra bontani annyi módosítással, hogy a 0-t csak átvitellel tudjuk felbontani. Emiatt az annál nagyobb helyiértéknél a felbontásban szereplő számjegyeknek páratlannak kell lenniük, vagy másképpen fogalmazva, azok felbontásában az egyik tagnak ott minden számjegye 0. Vagyis a fenti példán bemutatott helyiértékes felbontást el kell végeznünk, és az egyértelmű lesz. Abban minden szám egy páros, 0 és 18 közé eső szám valamilyen 10 hatvánnyal szorozva. A 0 és 18 közötti számok ennyiféleképpen bonthatók fel páratlan számjegyek összegére:
| 0 (5 db): |  |
 |
 |
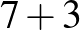 |
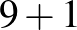 |
(extra átvitel!) |
| 2 (1 db): |  |
|||||
| 4 (2 db): |  |
 |
||||
| 6 (3 db): |  |
 |
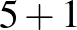 |
|||
| 8 (4 db): | 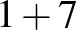 |
 |
 |
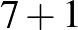 |
||
| 10 (5 db): |  |
 |
 |
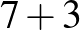 |
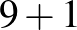 |
|
| 12 (4 db): | 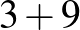 |
 |
 |
 |
||
| 14 (3 db): | 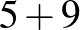 |
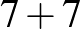 |
 |
|||
| 16 (2 db): |  |
 |
||||
| 18 (1 db): | 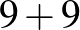 |
A helyiértékes felbontásban szereplő számokra ez alapján meg tudjuk mondani, hogy hányféleképpen tudjuk felírni azokat páratlan számjegy és egy csomó 0 alakú számok összegeként. Ezekből a felbontásokból az első tagokat összeadva is, és a második tagokat összeadva is erősen páratlan számokat kapunk, és ezek a különböző felbontások esetén különbözőek leszek. A fenti felbontásban a sorrend azért számít, mert így akkor az összes lehetséges felbontást megkapjuk. Ez alapján az összes lehetséges két erősen páratlan szám összegére bontás darabszáma nem más, mint a helyiértékes felbontások darabszámainak szorzata. A fenti példában
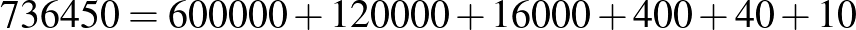 ,
,
így a 736450 számot 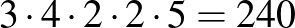 -féleképpen bonthatjuk erősen páratlan számok szorzatára. Példaként nézzünk egy „problémás” számot is, aminek azért van felbontása:
-féleképpen bonthatjuk erősen páratlan számok szorzatára. Példaként nézzünk egy „problémás” számot is, aminek azért van felbontása:
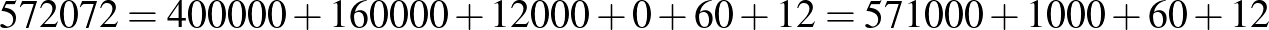 .
.
Ebben a felbontásban az 571000-et mindig az első összeadandóhoz „csapjuk hozzá”, a lehetséges kombinációkat meg fogja adni a többi tag erősen páratlanokra bontása. Így ebben az esetben 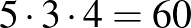 lehetséges erősen páratlan számra bontás van.
lehetséges erősen páratlan számra bontás van.
9. Marci bástyákat rak egy üres sakktáblára. Az első bástyát bárhová teheti, ezután minden újabb bástyát úgy tesz le, hogy az páratlan számú korábban elhelyezett bástyát tartson ütés alatt. Legfeljebb hány bástyát helyezhet a táblára Marci?
Megoldás: Bevallom, programot írtam rá, nem túl optimálisat, nem is biztos, hogy lehet olyat írni, ami végig is ellenőrzi az összes esetet. De elég sokáig elfutott a program ahhoz, hogy sejtést szerezzek a bizonyításhoz. Igaz, a sejtés hamis volt, de rávezetett a megoldásra.
A sakktábla mind a négy sarkába nem kerülhet bástya. Ugyanis a sarkokat csak 0, 1 vagy 2 bástya ütheti, és ha már három sarokban van bástya, akkor a negyedik sarkot már két bástya üti. És tudunk olyan megoldást adni, ami csak azt a sarkot nem tölti ki, minden mást igen. Könnyen ellenőrizhető, hogy az alábbi példában a megadott szabályok szerint raktuk le a bástyákat; itt a számok azt jelzik, hogy az adott mezőbe hányadik lépésben rakunk le bástyát:
| 1 | 63 | 55 | 47 | 39 | 31 | 23 | 8 |
| 2 | 62 | 54 | 46 | 38 | 30 | 22 | 15 |
| 3 | 61 | 53 | 45 | 37 | 29 | 21 | 14 |
| 4 | 60 | 52 | 44 | 36 | 28 | 20 | 13 |
| 5 | 59 | 51 | 43 | 35 | 27 | 19 | 12 |
| 6 | 58 | 50 | 42 | 34 | 26 | 18 | 11 |
| 7 | 57 | 49 | 41 | 33 | 25 | 17 | 10 |
| 56 | 48 | 40 | 32 | 24 | 16 | 9 |
10. Hányféleképp lehet egy 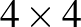 -es táblázat mezőiből néhányat pirosra festeni úgy, hogy minden sorban és minden oszlopban páros legyen a befestett mezők száma?
-es táblázat mezőiből néhányat pirosra festeni úgy, hogy minden sorban és minden oszlopban páros legyen a befestett mezők száma?
Megoldás: Fessük ki tetszőleges módon a táblázatunk bal felső 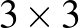 -as részét. Az, hogy minden sorban és oszlopban páros sok piros legyen, meghatározza az első három sor jobboldali, illetve az első három oszlop alsó mezőinek színet. Ebből az is következik, hogy a bal felső
-as részét. Az, hogy minden sorban és oszlopban páros sok piros legyen, meghatározza az első három sor jobboldali, illetve az első három oszlop alsó mezőinek színet. Ebből az is következik, hogy a bal felső 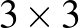 -as részben lévő pirosak számának paritása ugyanannyi, mint az első három sor végén lévő pirosak számának paritása, és ugyanannyi, mint az első három oszlop végén lévő pirosak számának paritása. Vagyis a jobb alsó sarokban lévő elem is egyértelműen tölthető ki ez alapján. Tehát a lehetséges kitöltések száma
-as részben lévő pirosak számának paritása ugyanannyi, mint az első három sor végén lévő pirosak számának paritása, és ugyanannyi, mint az első három oszlop végén lévő pirosak számának paritása. Vagyis a jobb alsó sarokban lévő elem is egyértelműen tölthető ki ez alapján. Tehát a lehetséges kitöltések száma 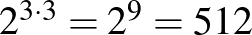 . Teljesen hasonló módon
. Teljesen hasonló módon 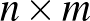 -es táblázat esetén a lehetséges kitöltések száma
-es táblázat esetén a lehetséges kitöltések száma 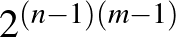 .
.
11. Igaz-e a következő állítás? Ha két ugyanakkora kerületű háromszögnek a területe is egyenlő, akkor a két háromszög egybevágó.
Megoldás: Nem igaz. Induljunk ki két elfajult, azonos kerületű háromszögből. Mindkettő legyen „egyenlő szárú”, az egyiknél a szárak essenek egybe és az alap hossza legyen 0, a másiknál a két szár adja ki az alap hosszát, és a magasság legyen 0. Mindkét háromszöget alakítsuk úgy, hogy menet közben maradjanak egyenlőszárúak, és a kerületük se változzon. Az elsőnél kezdjük el folytonos módon növelni az alap hosszát, a másiknál a magasságot. Mindaddig, amíg a két háromszög nem lesz szabályos, nem lehetnek egybevágóak: az első alapja mindig rövidebb lesz, mint a kerület harmada, a másodiké pedig mindig hosszabb lesz. Mindkét esetben igaz, hogy amíg az elfajult állapotból elérünk az egyenlő oldalú állapotig, addig a terület (a Heron-féle képlet alapján) folytonosan változik 0-tól a kerületnek megfelelő egyenlő oldalú háromszög területéig. Így Bolzano tétele alapján az első háromszög bármilyen állásához lesz a második háromszögnek olyan állása, amelynek pontosan ugyanaz lesz a területe. És ezzel az állítást beláttuk.
Egy kicsit formálisabban, legyen a kerület fele 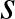 , az első háromszög alapjának hossza
, az első háromszög alapjának hossza  (így a szárai
(így a szárai 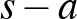 hosszúak), a második háromszög szárának hossza
hosszúak), a második háromszög szárának hossza 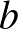 (így alapja
(így alapja  hosszú). A Heron-képlet szerint, ha területük egyenlő, akkor
hosszú). A Heron-képlet szerint, ha területük egyenlő, akkor
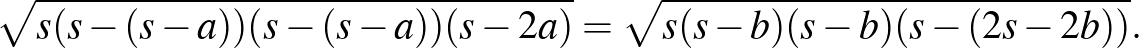
Az egyszerűség kedvéért legyen  (hasonlósággal mindig elérhető, és mivel úgyis ellenpéldát konstruálunk, akár vehetjük így hasonlóság nélkül is), így kapjuk, hogy
(hasonlósággal mindig elérhető, és mivel úgyis ellenpéldát konstruálunk, akár vehetjük így hasonlóság nélkül is), így kapjuk, hogy

Egy triviális megoldás (ami az első egyenlőségből látszik igazán jól) az 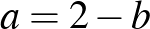 , ami pontosan annak felel meg, hogy a két háromszög egybevágó. A második egyenlőségben levő polinom ezek szerint osztható az
, ami pontosan annak felel meg, hogy a két háromszög egybevágó. A második egyenlőségben levő polinom ezek szerint osztható az 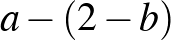 gyöktényezővel. Ha osztunk vele, akkor kapjuk az
gyöktényezővel. Ha osztunk vele, akkor kapjuk az
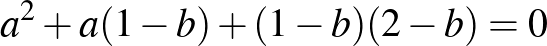
másodfokú egyenletet, ami megoldható:
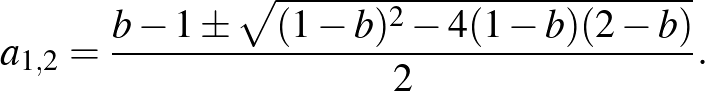
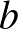 (amikor már nem elfajuló a háromszög) nyilván 1-nél nagyobb. Mivel a háromszög kerülete 4, a két
(amikor már nem elfajuló a háromszög) nyilván 1-nél nagyobb. Mivel a háromszög kerülete 4, a két 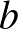 hosszú szár hossza darabonként kisebb, mint 2, vagyis
hosszú szár hossza darabonként kisebb, mint 2, vagyis 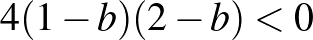 . Ebből tudjuk, hogy a fenti képletben a négyzetgyökvonás eredménye nagyobb, mint
. Ebből tudjuk, hogy a fenti képletben a négyzetgyökvonás eredménye nagyobb, mint  , így a két gyök közül csak a pozitív előjelű ad a háromszögoldal felének megfelelő pozitív számot, tehát
, így a két gyök közül csak a pozitív előjelű ad a háromszögoldal felének megfelelő pozitív számot, tehát
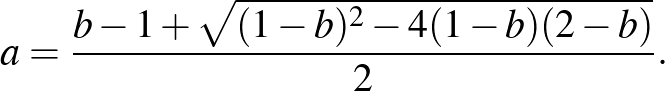
Eszerint valóban lehet találni nem egybevágó háromszögeket, amelyeknek azonos a területe és kerülete is. De hozzá kell tenni, hogy ezek közül nem mindegyik ad nem egybevágó háromszöget: 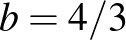 -ra
-ra 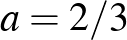 adódik, és ez megfelel az egyenlő oldalú háromszög esetének, de ez az egyetlen eset, amikor a háromszögek ebben az esetben egybevágóak.
adódik, és ez megfelel az egyenlő oldalú háromszög esetének, de ez az egyetlen eset, amikor a háromszögek ebben az esetben egybevágóak.
Érdekességképpen megjegyezzük, hogy a Wolfram Mathematica program meg tudja oldani a feladatban feladott egyenletrendszert. Ha 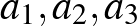 és
és 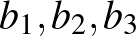 a háromszögek oldalai, akkor ezt az egyenletrendszert kell megoldani:
a háromszögek oldalai, akkor ezt az egyenletrendszert kell megoldani:
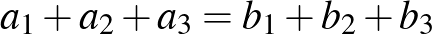
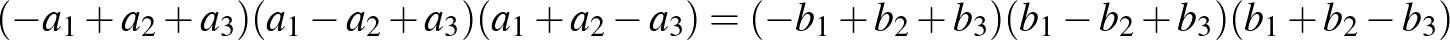
A megoldás többoldalas képleteket tartalmaz, amelyben persze szerepelnek azok az esetek is, amikor a két háromszög egybevágó (az oldalhosszak egymás valamilyen permutációi), de van más megoldás is. Ha ez alapján akarnánk igazolni, hogy nem teljesül az állítás, akkor ezeket a képleteket kellene megvizsgálnunk, hogy azok adnak-e nem egybevágó háromszögeket is, és mivel a képletek elég hosszúak és bonyolultak, épeszű ember nem kezd neki... ☺
12. Felföldön a parlament 40 szenátorból áll, mindegyikük munkáját 3-3 titkár segíti. A 40 szenátor és 120 titkár bizottságokban dolgozik, minden szenátor 6 bizottságnak, és minden titkár 2 bizottságnak a tagja. Egy bizottság vagy 5 szenátorból, vagy 3 szenátorból és 6 titkárból áll. Hány bizottság van összesen?
Megoldás: A 120 titkárnak van összesen 240 bizottsági tagsága, ezt csak a második típusú bizottságban tudják teljesíteni, és mivel azokban 6-6 titkár van, 40 darab második típusú bizottság van. A szenátoroknak szintén 240 bizottsági tagsága van, ebből a 40 darab második típusú bizottságban 120 tagság lekötődik, a fennmaradó 120 tagságot az első típusú bizottságban kell teljesíteniük, így abból 24 db van. Összesen tehát 64 bizottság van: 24 első és 40 második típusú.
A feladat formálisan egy lineáris egyenletrendszerre vezet. Ha 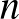 darab első típusú és
darab első típusú és  darab második típusú bizottság van, akkor a feltételek alapján
darab második típusú bizottság van, akkor a feltételek alapján
 ,
, 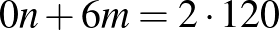 .
.
És ez egyértelműen megoldható, mert az egyenletek lineárisan függetlenek.
13. Sandokan és öt kalóza egy asztal körül ülnek, hogy elosszák a zsákmányolt 99 aranyat. Sandokan javaslatot tesz arra, hogy kinek hány arany jusson, ezután az öt kalóz szavaz erről. Egy kalóz igent mond a javaslatra, ha neki több arany jut, mint két szomszédjának összesen. A javaslat szerint osztoznak az aranyon, ha legalább hárman mellette szavaznak. Ha kevesebb a támogató szavazat, akkor Sandokan a szerencsétlen javaslata miatt semmit sem kaphat a zsákmányból. Legfeljebb hány aranyat tud megszerezni Sandokan?
Megoldás: Vegyük észre, hogy két szomszédos kalóz közül legfeljebb az egyik szavazza meg a javaslatot, hiszen mindkettőre igaz az, hogy megszavazáshoz többet kell kapjon, mint bármelyik szomszédja. Vagyis Sandokan szomszédainak és a vele szemben ülőnek kell megszavaznia a javaslatot. Mivel a fennmaradó két kalóz úgysem szavazza meg a javaslatot, ne pazaroljuk az aranyakat rájuk, a javaslat szerint kapjanak 0 aranyat. Sandokan két szomszédjának legalább eggyel több aranyat kell kapnia, mint Sandokannak, de a szemben ülőnek is juttatni kell legalább egy aranyat, hogy megszavazzák a javaslatot. Így Sandokantól indulva körbe a Sandokan számára legjobb javaslat: 32, 33, 0, 1, 0, 33.
Ha (Sandokanon kívül) páratlan sok kalóz van, és legalább a felüknek meg kell szavaznia a javaslatot, akkor a fenti okoskodással meghatározható, hogy hány aranyat tud megszerezni Sandokan saját magának. A javaslat megint úgy fog szólni, hogy a szomszédai eggyel több aranyat kapjanak, mint ő, és minden második kalóz kapjon még 1-1 aranyat. Ha ez nem adja ki a teljes aranymennyiséget, akkor a Sandokannak szimpatikusabb kalózok kaphatnak többet is... ☺. Például 9 kalóz és 99 arany esetén a minimalista javaslat a 31, 32, 0, 1, 0, 1, 0, 1, 0, 32 lenne, de ez összesen csak 98 arany.
Ha (Sandokanon kívül) páros sok kalóz van, és még mindig legalább a felüknek meg kell szavaznia a javaslatot, akkor is használható fenti okoskodás. Ilyenkor csak az egyik szomszédnak, és tőle számítva minden második kalóznak kell megszavaznia a javaslatot. A szomszéd most is kapjon eggyel több aranyat, mint Sandokan, a többi javaslatot megszavazó kalóz 1-1 aranyat, a többiek semmit. Itt sem biztos, hogy „kijön” a teljes aranymennyiség, például 8 kalóz és 99 arany esetén 42, 43, 0, 1, 0, 1, 0, 1, 0 lenne a minimális javaslat és ez megint csak 98 arany.
Érdekes, hogy ugyanezeket a megoldásokat kapjuk akkor is, ha egy kalóz már akkor is megszavazza a javaslatot, ha mindkét szomszédja kevesebb aranyat kap, mint ő.
Ha a kalózok felénél kevesebb szavazat is elég a javaslat elfogadásához, akkor Sandokan legjobb stratégiája, hogy a szomszédainak nem javasol aranyat, és egymástól legalább 2 távolságra levő, a javaslat megszavazásához szükséges számú kalóznak ad 1-1 aranyat, a többieknek semmit. Így az aranyakból a szükséges szavazatok számával kevesebbet meg tud szerezni.
Ha a kalózok felénél legalább eggyel több szavazat kell a javaslat elfogadásához, akkor Sandokan a megoldás első mondatában megfogalmazottak szerint mindenképpen hoppon marad.
Azt is érdemes meggondolni, hogy mi a helyzet, ha egy kalóz már akkor igennel szavaz, ha legalább az egyik szomszédjánál több aranyat kap. Ez ugyanis közelebb állhat egy kalóz lelkivilágához, hiszen ezzel biztosítva van, hogy nem ő kapja a legkevesebb aranyat. Ilyenkor optimálisan szomszédos kalózpároknak oszthatunk ki 1-1 aranyat úgy, hogy a szomszédjukban ülők ne kapjanak semmit, mert akkor ők már megszavazzák a javaslatot. Itt kevés kalóz esetén szükség van egy kis trükközésre; ha 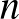 arany van és
arany van és 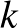 kalóz, akkor az optimális javaslatok így néznek ki (ahol
kalóz, akkor az optimális javaslatok így néznek ki (ahol 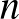 persze elég nagy kell legyen, hogy Sandokannak is maradjon arany):
persze elég nagy kell legyen, hogy Sandokannak is maradjon arany):
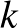 |
javaslat |
| 1 | ![$[(n-1)/2]$](/images/stories/latexuj/2023-11/2023-11-7tusa2megjegyzes/img68.png) , , ![$n-[(n-1)/2]$](/images/stories/latexuj/2023-11/2023-11-7tusa2megjegyzes/img69.png) |
| 2 | 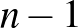 , 1, 0 , 1, 0 |
| 3 |  , 2, 1, 0 , 2, 1, 0 |
| 4 |  , 0, 1, 1, 0 , 0, 1, 1, 0 |
| 5 |  , 0, 1, 1, 0, 1 , 0, 1, 1, 0, 1 |
| 6 |  , 0, 1, 1, 0, 1, 0 , 0, 1, 1, 0, 1, 0 |
| 7 |  , 0, 1, 1, 0, 1, 1, 0 , 0, 1, 1, 0, 1, 1, 0 |
| 8 |  , 0, 1, 1, 0, 1, 1, 0, 0 , 0, 1, 1, 0, 1, 1, 0, 0 |
| 9 |  , 0, 1, 1, 0, 1, 1, 0, 1, 0 , 0, 1, 1, 0, 1, 1, 0, 1, 0 |
| 10 |  , 0, 1, 1, 0, 1, 1, 0, 1, 0, 0 , 0, 1, 1, 0, 1, 1, 0, 1, 0, 0 |
Itt is az a helyzet, hogy legalább 4 kalóz esetén az aranyakból a szükséges szavazatok számával kevesebbet meg tud szerezni.
14. Egy tízfős társaság több megbeszélést tartott. Minden egyes találkozón a tíz emberből öten vettek részt. A társaságnak nincs két olyan tagja, akik együtt három megbeszélésen is jelen lettek volna. Legfeljebb hány találkozóra kerülhetett sor?
Megoldás: Programot írtam rá, és az azt mondta, hogy maximum 8 találkozó lehetett, és adott is rá példát (a számok 0-tól 9-ig jelölik, hogy melyik találkozón melyik emberek vettek részt):
 ,
, 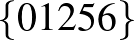 ,
, 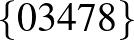 ,
, 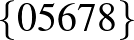 ,
, 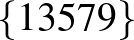 ,
, 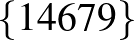 ,
, 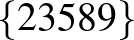 ,
, 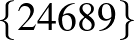 .
.
Próbáljuk meg bebizonyítani, hogy 8-nál több találkozóra nem kerülhet sor. 10 emberből párokat 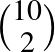 -féleképpen lehet kiválasztani. Ezek a párok maximum 2-2 találkozón vehetnek részt, így a párok
-féleképpen lehet kiválasztani. Ezek a párok maximum 2-2 találkozón vehetnek részt, így a párok 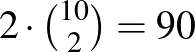 részvételt produkálhatnak. Mivel egy találkozón 5 ember vagyis
részvételt produkálhatnak. Mivel egy találkozón 5 ember vagyis  pár vesz részt, ezért minden találkozót 10-szer számoltunk, tehát a találkozó száma maximum 90/10=9 lehet. Ezt csak akkor lehet elérni, ha (szimmetria okok miatt) mindenki pontosan ugyanannyi találkozón vesz részt, de a 9 találkozó darabonkénti 5 részvételét, vagyis 45-öt nem lehet 10 emberre egyenletesen szétosztani. Vagyis a találkozók száma tényleg nem lehet több, mint 8.
pár vesz részt, ezért minden találkozót 10-szer számoltunk, tehát a találkozó száma maximum 90/10=9 lehet. Ezt csak akkor lehet elérni, ha (szimmetria okok miatt) mindenki pontosan ugyanannyi találkozón vesz részt, de a 9 találkozó darabonkénti 5 részvételét, vagyis 45-öt nem lehet 10 emberre egyenletesen szétosztani. Vagyis a találkozók száma tényleg nem lehet több, mint 8.
Általánosítsunk egy kicsit. Legyen 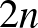 ember, akik
ember, akik 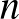 fős találkozókra mennek úgy, hogy nincs olyan pár, akik három talákozón is résztvesz. A fenti számolás alapján a találkozók száma maximum
fős találkozókra mennek úgy, hogy nincs olyan pár, akik három talákozón is résztvesz. A fenti számolás alapján a találkozók száma maximum
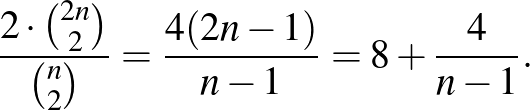
Ez a mennyiség pozitív irányból, monoton csökkenve tart 8-hoz, miközben 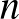 tart végtelenbe, és
tart végtelenbe, és 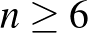 esetén már kisebb, mint 9.
esetén már kisebb, mint 9. 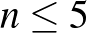 -re kiszámolva ezeket (programmal) könnyen találhatunk maximális számú találkozót, ami 4 és 5 esetén nem éri el a számolás alapján elvileg leheséges 9 találkozót, azoknál csak 8 találkozót tudunk létrehozni.
-re kiszámolva ezeket (programmal) könnyen találhatunk maximális számú találkozót, ami 4 és 5 esetén nem éri el a számolás alapján elvileg leheséges 9 találkozót, azoknál csak 8 találkozót tudunk létrehozni.
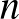 |
becslés | egy lehetséges találkozó kiosztás |
| 2 | 12 |   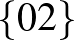 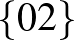 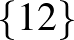 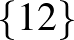 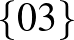 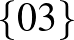 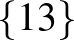 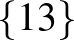 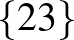 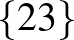 |
| 3 | 10 | 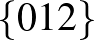  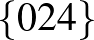 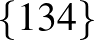 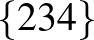 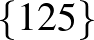 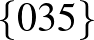 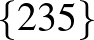 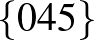 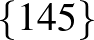 |
| 4 | 9 | 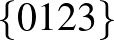 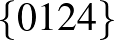 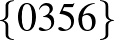  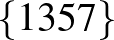 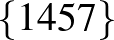 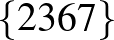 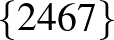 |
| 5 | 9 |  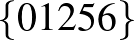 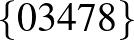 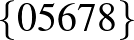 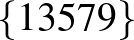 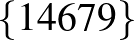 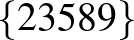 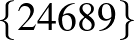 |
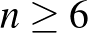 -ra a becslés alapján nem lehet több találkozó, mint 8. 6 és 7 esetén a program még kivárható időn belül lefut, és például a következő találkozó-kiosztásokat adja:
-ra a becslés alapján nem lehet több találkozó, mint 8. 6 és 7 esetén a program még kivárható időn belül lefut, és például a következő találkozó-kiosztásokat adja:
 :
:  ,
, 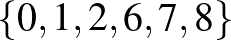 ,
,  ,
, 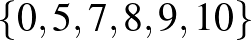 ,
, 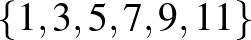 ,
, 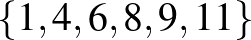 ,
,  ,
, 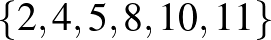 .
.
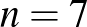 :
: 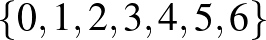 ,
,  ,
, 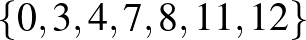 ,
, 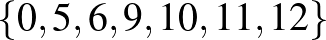 ,
, 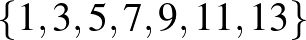 ,
, 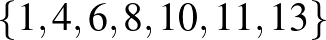 ,
, 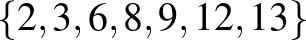 ,
, 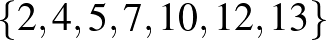 .
.
Ebből a sejtés nyilvánvalóan az, hogy 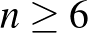 -ra 8 találkozó mindig megszervezhető. De a sejtés nem igaz, és erre is a program vezetett rá. Valami mintát kerestem abban, hogy hogyan osszuk el az embereket a találkozók között. Ehhez (többek között) kiírattam a programmal, hogy az egyes emberek hányadik találkozókon vettek részt. Mivel 8 találkozó van, az így keletkező kombinációk száma véges:
-ra 8 találkozó mindig megszervezhető. De a sejtés nem igaz, és erre is a program vezetett rá. Valami mintát kerestem abban, hogy hogyan osszuk el az embereket a találkozók között. Ehhez (többek között) kiírattam a programmal, hogy az egyes emberek hányadik találkozókon vettek részt. Mivel 8 találkozó van, az így keletkező kombinációk száma véges:  (mellesleg, úgy tűnik, hogy egy ember mindig pontosan 4 találkozón vesz részt, így a kombinációk száma még kevesebb:
(mellesleg, úgy tűnik, hogy egy ember mindig pontosan 4 találkozón vesz részt, így a kombinációk száma még kevesebb:  ). Ez azt jelenti, hogy ha legalább 257 emberrel próbálnánk meg a találkozókat megszervezni, akkor a skatulya-elv szerint lenne két ember, akik pontosan ugyanazokra a találkozókra mentek el. Ha ez legalább három találkozó, akkor a kiosztás nem felel meg a feltételeknek. Ha pedig legfeljebb 2 ilyen találkozó van, akkor mindkét emberre igaz az, hogy a találkozókon (rajtuk kívül) legfeljebb
). Ez azt jelenti, hogy ha legalább 257 emberrel próbálnánk meg a találkozókat megszervezni, akkor a skatulya-elv szerint lenne két ember, akik pontosan ugyanazokra a találkozókra mentek el. Ha ez legalább három találkozó, akkor a kiosztás nem felel meg a feltételeknek. Ha pedig legfeljebb 2 ilyen találkozó van, akkor mindkét emberre igaz az, hogy a találkozókon (rajtuk kívül) legfeljebb  másik emberrel találkozhatnak (multiplicitással számolva), ők pedig kétszer találkoznak. Vagyis ez a két ember a találkozóbeli párok számához
másik emberrel találkozhatnak (multiplicitással számolva), ők pedig kétszer találkoznak. Vagyis ez a két ember a találkozóbeli párok számához 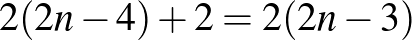 -al járul hozzá, a többiek legfeljebb
-al járul hozzá, a többiek legfeljebb 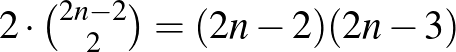 párral, ami összesen
párral, ami összesen  pár. Egy találkozón
pár. Egy találkozón  pár vesz részt, így a találkozók száma legfeljebb
pár vesz részt, így a találkozók száma legfeljebb
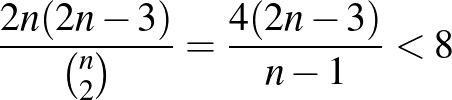
lehet, ami ellentmond annak, hogy ki tudnánk osztani az embereket 8 találkozóra is. Érdekes eredmény, de azért valahol várható is: mivel az első becslésünk alapján a találkozók számának felső becslése tart 8-hoz, egyre optimálisabban kellene kiosztanunk az embereket, és úgy tűnik, hogy ez egy idő után már nem megy.
De tovább is tudunk menni. Megnézve a feladat hivatalos megoldását, valóban be lehet látni, hogy egy ember legfeljebb 4 találkozón vesz részt. Ugyanis ha egy ember minden másikkal legfeljebb 2-szer találkozik, akkor összesen (multiplicitással) maximum  párban vesz részt. Ha viszont 5 találkozón venne részt, akkor
párban vesz részt. Ha viszont 5 találkozón venne részt, akkor 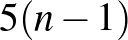 párban lenne benne, de
párban lenne benne, de 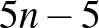 nagyobb, mint
nagyobb, mint 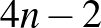 , ha
, ha 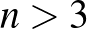 , így ez nem lehetséges. Másrészt ha produkálni szeretnénk a 8 találkozót, akkor azokon összesen
, így ez nem lehetséges. Másrészt ha produkálni szeretnénk a 8 találkozót, akkor azokon összesen 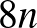 ember vesz részt, így mindenkinek pontosan 4 találkozón kell megjelennie, hogy ezt végre tudjuk hajtani. Ráadásul ezt úgy kell megtenniük, hogy semelyik két ember ne legyen ott három találkozón. Ha a találkozókon való megjelenést kettes számrendszerben ábrázoljuk minden emberre úgy, hogy egy adott helyiértéken levő 0 számjegy jelenti, hogy nem jelent meg azon a találkozón az illető, és az 1, hogy igen, akkor ezek 8 jegyű számok lesznek (amik kezdődhetnek 0-val is). A jelenléti feltétel erre átfogalmazva azt jelenti, hogy bármelyik két számra igaz, hogy legfeljebb 2 helyiértéken lehet mindkét számban 1-es. De mivel a számokban 4-4 darab 0-s és 1-es számjegy van, ez azt is jelenti, hogy legfeljebb 2 helyiértéken lehet mindkét számban 0-s, tehát a két szám legfeljebb 4 helyiértéken egyezhet meg. Azt, hogy a két bináris szám hány helyiértéken tér el, az irodalomban Hamming-távolságnak hívják; itt a feltétel eszerint az, hogy bármely két szám Hamming-távolsága legalább 4 legyen. Egy egyszerű programmal ellenőrizhető, hogy ilyen számokból legfeljebb 14 darab van, például ezek:
ember vesz részt, így mindenkinek pontosan 4 találkozón kell megjelennie, hogy ezt végre tudjuk hajtani. Ráadásul ezt úgy kell megtenniük, hogy semelyik két ember ne legyen ott három találkozón. Ha a találkozókon való megjelenést kettes számrendszerben ábrázoljuk minden emberre úgy, hogy egy adott helyiértéken levő 0 számjegy jelenti, hogy nem jelent meg azon a találkozón az illető, és az 1, hogy igen, akkor ezek 8 jegyű számok lesznek (amik kezdődhetnek 0-val is). A jelenléti feltétel erre átfogalmazva azt jelenti, hogy bármelyik két számra igaz, hogy legfeljebb 2 helyiértéken lehet mindkét számban 1-es. De mivel a számokban 4-4 darab 0-s és 1-es számjegy van, ez azt is jelenti, hogy legfeljebb 2 helyiértéken lehet mindkét számban 0-s, tehát a két szám legfeljebb 4 helyiértéken egyezhet meg. Azt, hogy a két bináris szám hány helyiértéken tér el, az irodalomban Hamming-távolságnak hívják; itt a feltétel eszerint az, hogy bármely két szám Hamming-távolsága legalább 4 legyen. Egy egyszerű programmal ellenőrizhető, hogy ilyen számokból legfeljebb 14 darab van, például ezek:
11110000, 11001100, 00111100, 10101010, 01011010, 01100110, 10010110,
00001111, 00110011, 11000011, 01010101, 10100101, 10011001, 01101001.
Ezek szerint 14 ember esetén 8 találkozót össze lehet hozni, és ezt már a korábbi programunk is tudta produkálni. Mivel a számok itt párban vannak abban az értelemben, hogy ha egy szám szerepel a listán, akkor az egyes komplemense (amelyikben minden számjegyet kicserélünk 0-ról 1-re vagy 1-ről 0-ra, a fenti listában egymás alatt vannak ezek a számok) is benne van, ezért ilyen párokat elhagyva minden találkozóról 1-1 embert veszünk ki, és így 12, 10 és 8 ember esetén is van megfelelő kiosztás (de ezt is tudtuk korábbról).
Mi a helyzet az 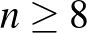 esetekkel? Az biztos, hogy 4 találkozó akárhány emberrel megszervezhető: az emberek egyik fele menjen el kétszer találkozni egymással, a másik fele is csinálja ugyanazt, és megvan a 4 találkozó. És persze az is igaz, hogy ha 8 találkozót meg lehet rendezni 14 emberrel, akkor 7, 6, és 5 találkozót is meg lehet rendezni ugyanannyi emberrel (néhány találkozó elmarad). Nem sikerült olyan szabályosságot találnom, ami megmagyarázná az eredményt, de a programom szerint 7 találkozó még mindig csak 14 emberrel valósítható meg:
esetekkel? Az biztos, hogy 4 találkozó akárhány emberrel megszervezhető: az emberek egyik fele menjen el kétszer találkozni egymással, a másik fele is csinálja ugyanazt, és megvan a 4 találkozó. És persze az is igaz, hogy ha 8 találkozót meg lehet rendezni 14 emberrel, akkor 7, 6, és 5 találkozót is meg lehet rendezni ugyanannyi emberrel (néhány találkozó elmarad). Nem sikerült olyan szabályosságot találnom, ami megmagyarázná az eredményt, de a programom szerint 7 találkozó még mindig csak 14 emberrel valósítható meg:
1111000, 1100110, 0011110, 1010101, 0101101, 0110011, 1001011,
0000111, 0011001, 1100001, 0101010, 1010010, 1001100, 0110100.
A 6 és az 5 találkozó már 20 emberrel is működik:
111000, 110100, 101100, 011100, 110010, 101010, 011010, 100110, 010110, 001110,
000111, 001011, 010011, 100011, 001101, 010101, 100101, 011001, 101001, 110001,
illetve
11000, 11100, 11010, 10110, 01110, 11001, 10101, 01101, 10011, 01011,
00111, 00011, 00101, 01001, 10001, 00110, 01010, 10010, 01100, 10100.
Néhány érdekesség (szintén magyarázat nélkül).  , 7 és 8 esetén permutációtól eltekintve egyetlen megoldás van, és az egyes komplemens párokból áll.
, 7 és 8 esetén permutációtól eltekintve egyetlen megoldás van, és az egyes komplemens párokból áll. 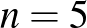 -re vannak nem egyes komplemens párokból álló megoldások is, de az egyes komplemens párokból álló megoldás permutációtól eltekintve szintén egyértelmű.
-re vannak nem egyes komplemens párokból álló megoldások is, de az egyes komplemens párokból álló megoldás permutációtól eltekintve szintén egyértelmű. 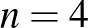 -re viszont egyes komplemens párokból álló megoldásból is sok van, hiszen bármilyen módon osztjuk két egyenlő részre az emberek halmazát, azok a részhalmazok, mint a találkozók résztvevői, megfelelőek lesznek. És további, ennél bonyolultabb megoldások is vannak.
-re viszont egyes komplemens párokból álló megoldásból is sok van, hiszen bármilyen módon osztjuk két egyenlő részre az emberek halmazát, azok a részhalmazok, mint a találkozók résztvevői, megfelelőek lesznek. És további, ennél bonyolultabb megoldások is vannak.
Ezt a kutatást a TKP2021-NVA-09 projekt támogatta. A TKP2021-NVA-09 számú projekt a Magyar Innovációs és Technológiai Minisztérium támogatásával valósult meg a Nemzeti Kutatási, Fejlesztési és Innovációs Alapból, a TKP2021-NVA támogatási konstrukció keretében.











