Hogyan lett egy Héttusa-feladatból Schweitzer-probléma?

A Héttusa verseny még nagyon fiatal: fél éve indult, és egyelőre csak reméljük, hogy legalább olyan hosszú életű lesz, mint a patinás és az egész világon ismert és méltán elismert Schweitzer-verseny [1]. Ez utóbbi 1949 óta kifejezetten a legkiválóbb egyetemi hallgatók versenye, amelyről egy korábbi Érintő-cikkben is írtunk [2].

Ezért is különleges, hogy az idei verseny egyik feladata, amelyet Makay Géza, az SZTE Bolyai Intézetének docense javasolt, a júniusi Érintőben megjelent Héttusa egyik feladatából nőtt ki [3]:

Feladat: Van-e olyan szám, amelynek pontosan tíz pozitív osztója van a 20-nál nem nagyobb számok között?

Megoldás: Mivel oszthatóságról, osztókról van szó, az embernek óhatatlanul eszébe jut a prímfelbontás. A keresett számunk legyen

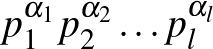
$\displaystyle p_1^{\alpha_1}p_2^{\alpha_2}\ldots p_l^{\alpha_l}$

alakú, ahol a 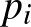$p_i$ -k különböző prímek, 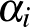$\alpha_i$ -k pedig pozitív egészek. Feltehetjük, hogy 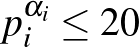$p_i^{\alpha_i}\leq 20$ , hiszen ha egy prímhatvány 20-nál nagyobb, akkor minden osztó, amelyben az tényezőként szerepel, szintén 20-nál nagyobb lesz. Kezdjük felépíteni egy egyszerű „mohó algoritmussal”¹ a számunkat prímhatvány tényezőnként (a legkisebb prímtől kiindulva) úgy, hogy a 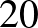$20$ -nál nem nagyobb osztók száma ne lépje túl a 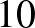$10$ -et:

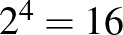;	a 20-nál nem nagyobb osztóinak száma 5,
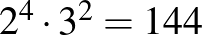$2^4\cdot 3^2=144$ ;	a 20-nál nem nagyobb osztóinak száma 10.

És a feladatot megoldottuk.

A feladat elég könnyen megoldható egyszerű számolással. De muszáj rögtön megoldást találni? Nem élvezhetnénk egy kicsit magát a problémát? ☺

A következő kérdéseket lehet feltenni:

1. kérdés: Milyen alakú számok jöhetnek szóba megoldásként?

Megoldás: Már pedzegettük a kérdést a feladat megoldásában: olyan megoldásokat keresünk, ahol a számnak nincs 20-nál nagyobb 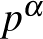$p^\alpha$ osztója, tehát ezek a prímhatványok jöhetnek szóba:

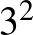$2^4$ , $3^2$ , 5, 7, 11, 13, 17, 19.

Más szóval a lényegesen különböző megoldások a

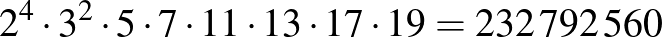
$\displaystyle 2^4\cdot3^2\cdot5\cdot7\cdot11\cdot13\cdot17\cdot19=232\,792\,560$

osztói közül kerülhetnek ki. Az osztókból véges sok van, ellenőrizhető, hogy közülük melyek megoldások (ld. a következő kérdést). Egy megoldásból újabb megoldást kapunk, ha egy olyan prímhatvánnyal szorozzuk meg, amellyel megszorozva nem keletkezik újabb 20-nál kisebb osztó. Ilyen lehet egy 20-nál nagyobb prím hatványa, de lehet például a 2 valamilyen pozitív egész hatványa is, hiszen ez utóbbi esetben a 2 legalább az 5-en szerepelne, ami már nagyobb, mint 20. 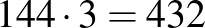Például a $144\cdot 2=288$ és a $144\cdot 3=432$ megoldások, nem megoldás a 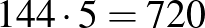$144\cdot 5=720$ , de megoldás a 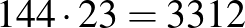$144\cdot 23=3312$ . Ezzel a módszerrel megkaphatjuk az összes megoldást.

A megoldáshalmaz egy érdekes tulajdonsága, hogy a megoldások 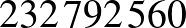$232\,792\,560$ -periodikusan helyezkednek el a számegyenesen. Ez azért teljesül, mert egy megoldás azért megoldás, mert a 2, 3, 5, 7, 11, 13, 17, 19 prímek olyan hatványon szerepelnek benne, amilyenen, és ez nem változik a 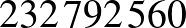$232\,792\,560$ -nal való eltolással. Ebben a kijelentésben azért van egy kis csúsztatás: ha a megoldásban az egyik prím maximális (vagy annál nagyobb) hatványon szerepel, akkor az eltolással neki változhat a kitevője, de nem csökkenhet a maximális kitevő alá, és ez a 20-nál kisebb osztók számát nem befolyásolja.

2. kérdés: 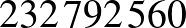$232\,792\,560$ -nak hány olyan pozitív osztója van, amelynek pontosan tíz pozitív osztója van a 20-nál nem nagyobb számok között?

Megoldás: 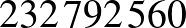$232\,792\,560$ osztóiból az ismert állítás alapján

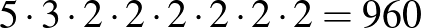
$\displaystyle 5\cdot3\cdot2\cdot2\cdot2\cdot2\cdot2\cdot2=960$

darab van, így ezt már nem szívesen ellenőrizné az ember „kézzel”, érdemes programot írni rá.

De ha már emlegettük az „ismert állítást”, ne essünk neki teljesen naív módon az osztók keresésének végignézve a számokat 1-től 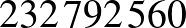$232\,792\,560$ -ig: a trükk az állítás bizonyításában, hogy az osztókban minden prímtényező kitevője lehet bármi 0-tól a számban található kitevőig, hát listázzuk ez alapján az osztókat a programban.

Nyilván tovább is fogunk általánosítani, tehát ne direktben erre a 20-as számra írjuk meg a programunkat, hanem általánosabban: 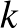$k$ darab osztót fogunk keresni, amelyek nem nagyobbak 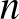$n$ -nél.

Amikor az ember elkezd gondolkodni egy program megírásán, akkor végig kell gondolnia, hogy mit hogyan kíván „modellezni” a programban, mit hogyan kell tárolni, melyik adatot hogyan kell kezelni és milyen algoritmus alapján fog dolgozni a program.

Az algoritmus a KöMaL-ban megjelent cikkben [4] részletesen szerepel, ennek alapján a kérdésre a válasz, hogy összesen 84 darab számnak van 10 db 20-nál nem nagyobb osztója.

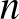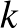A programmal különféle $n$ és $k$ számokkal kísérletezve mindig találunk megfelelő számot, ráadásul kiderül az is, hogy a fenti mohó algoritmus ezekben az esetekben mindig működik. Ennek következménye a következő

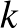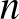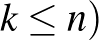Állítás: A fenti mohó algoritmussal lehet találni olyan természetes számot, amelynek pontosan db pozitív osztója van az -nél nem nagyobb számok között ( $k\leq n)$ .

Megoldás: Ennek az állításnak egy egyszerűbb (?) változata volt a 2023. évi Schweitzer Miklós Matematikai Emlékverseny egyik feladata, amelyben a mohó algoritmusra való utalás nélkül és csak elegendően nagy 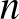$n$ -ekre kellett belátni az állítást. A kitűzés már megjelent, és a bizonyítás is hamarosan felkerül a Bolyai Társulat honlapjára [5]. (A nem hivatalos megoldások itt találhatóak.) Ez az állítás annyival több annál a feladatnál, hogy ezt minden 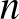$n$ -re be kell látnunk. A megjelent bizonyítás nem foglalkozik azzal a kérdéssel, hogy konkrétan milyen nagy 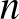$n$ -ektől kezdve teljesül az állítás, de óvatosabb becsléseket alkalmazva ellenőrizhető, hogy 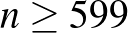$n\geq 599$ esetére is adható hasonló bizonyítás. Az pedig egy elég optimálisan megírt programmal pár másodperc alatt megmutatható, hogy 599-nél kisebb 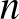$n$ -ekre is igaz az állítás.

Ezt a kutatást a TKP2021-NVA-09 projekt támogatta. A TKP2021-NVA-09 számú projekt a Magyar Innovációs és Technológiai Minisztérium támogatásával valósult meg a Nemzeti Kutatási, Fejlesztési és Innovációs Alapból, a TKP2021-NVA támogatási konstrukció keretében.

Irodalomjegyzék

: [1] https://www.bolyai.hu/versenyek-schweitzer-miklos-emlekverseny/
: [2] https://ematlap.hu/index.php/interju-portre-2017-03/417-schweitzer-2016-jelentes
: [3] https://ematlap.hu/fooldal-2023-2
: [4] Makay Géza: Matematika és informatika – kéz a kézben, avagy Egy 2023-as Schweitzer példa előzménye, KöMaL, 2024. januári szám, megjelenés alatt.
: [5] https://www.bolyai.hu/versenyek-schweitzer-miklos-emlekverseny/

Makay Géza

Szegedi Tudományegyetem, Bolyai Intézet

Lábjegyzet

: ¹ A mohó algoritmus olyan döntéshozó algoritmus, amely minden egyes lépésnél a legjobbnak tűnő döntést hozza a rendelkezésre álló lehetőségek közül, anélkül hogy előretekintene.