A Héttusa verseny második fordulójának feladatait (8–14. feladatok) 2023. szeptemberi számunkban tűztük ki.
Míg az 1. forduló feladataira 19 beküldőtől 69 jó választ kaptunk, most a 2. fordulóban 85 jó válasz érkezett 18 beküldőtől.
A feladatok nehézségi sorrendjét jelzi a beérkezett helyes válaszok száma:
| A feladat sorszáma | 8. | 9. | 10. | 11. | 12. | 13. | 14. |
| A beérkezett helyes válaszok száma | 13 | 8 | 9 | 14 | 16 | 15 | 10 |
A következő táblázat mutatja, hogy a legeredményesebb beküldők mely feladatokra adtak helyes választ. (Vannak, akik a saját nevükkel szerepelnek, és vannak, akik más nevet választottak maguknak.)
| A feladat sorszáma | 8. | 9. | 10. | 11. | 12. | 13. | 14. |
| Kovach M. László | X | X | X | X | X | X | X |
| Makay Géza | X | X | X | X | X | X | X |
| Belzebub | X | X | X | X | X | X | X |
| Orangestripes | X | X | X | X | X | X | |
| Ujházy Márton | X | X | X | X | X | X | |
| Vaszary Krisztián | X | X | X | X | X | X | |
| Jankó Zsuzsanna | X | X | X | X | X | X | |
| Danka Emma | X | X | X | X | X | ||
| Megérek egy Petákot | X | X | X | X | X | ||
| Szemerédi Ferenc | X | X | X | X | X | ||
| D & 2d | X | X | X | X | |||
| Drágos Rolland | X | X | X | X | |||
| Nicolcescu Magdalena | X | X | X | X | |||
| Berkó Erzsébet | X | X | X | X |
Fordulónként a legjobb megoldók közül néhányan könyvjutalmat kapnak. A három diák közül Danka Emma, a felnőttek kategóriájában versenyzők közül pedig Vaszary Krisztián kapott a mostani forduló után jutalomkönyvet. A Typotex kiadó kínálatából ezeket a könyveket választották:
Pintér Gergő: Új világok teremtése. Geometriai képzetek és képződmények, Typotex, 2020
Róka Sándor: Válogatás Erdős Pál kedvenc feladataiból, Typotex, 2023
A 4. forduló után az élmezőnyt (10-20 versenyzőt) jutalmazzuk. Ehhez ajándék könyveket ajánlott fel a Bolyai János Matematikai Társulat és a Szegedi Tudományegyetem Bolyai Intézete. Húsznál több könyvből választhatnak a versenyzők, a Bolyai Társulat és a Springer közös köteteiből, illetve a Polygon kiadványaiból.
https://www.bolyai.hu/files/KOTETEK_Springer_kozos_kotetek.pdf
https://www.math.u-szeged.hu/polygon/konyvtar.htm
https://www.math.u-szeged.hu/polygon/jegyzet.htm
A feladatok megoldása
8. Igaz-e, hogy bármely pozitív páros szám előáll két olyan szám összegeként, amelyek mindegyike páratlan számjegyekből áll?
Megoldás. A válasz: Hamis az állítás.
Például a 300 nem áll elő két olyan szám összegeként, amelyek mindegyike páratlan számjegyekből áll.
Ha 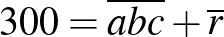 , akkor
, akkor 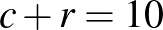 , ezért
, ezért 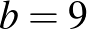 , és
, és 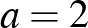 , ami páros.
, ami páros.
Ha 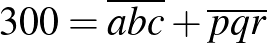 , vagy
, vagy 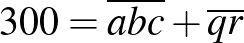 , akkor
, akkor 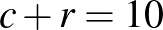 , ezért
, ezért 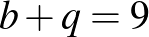 , és itt
, és itt 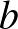 vagy
vagy 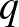 páros. (
páros. (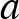 ,
, 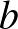 ,
, 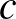 ,
, 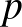 ,
, 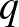 ,
, 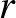 mind 0 és 9 közötti számjegyek.)
mind 0 és 9 közötti számjegyek.)
9. Marci bástyákat rak egy üres sakktáblára. Az első bástyát bárhová teheti, ezután minden újabb bástyát úgy tesz le, hogy az páratlan számú korábban elhelyezett bástyát tartson ütés alatt. Legfeljebb hány bástyát helyezhet a táblára Marci?
Megoldás. A válasz: 63.
Helyezzünk három bástyát az 1. ábra szerint a számok sorrendjében a tábla sarkaiba.
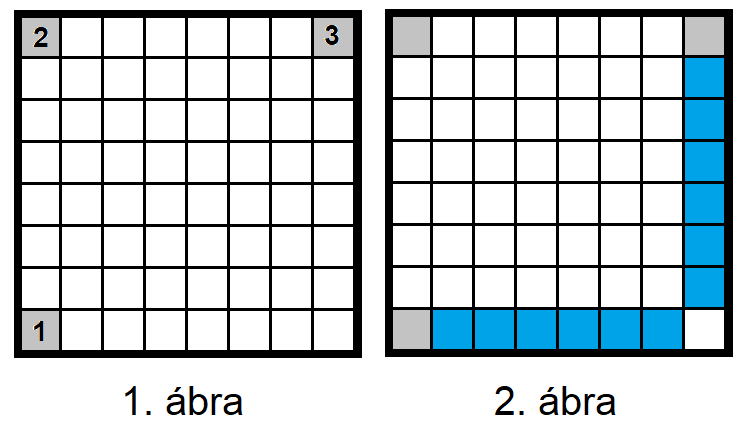
Ezután ahogyan a 2. ábra mutatja, töltsük fel az alsó sort balról jobbra, és a jobb szélső oszlopot fentről lefelé. (A kék mezőkre pakoljuk a bástyákat.)
Folytassuk az oszlopok feltöltésével, alulról felfelé haladva. Előbb a bal szélső oszlopot (3. ábra), majd a mellette lévőt, és így tovább.
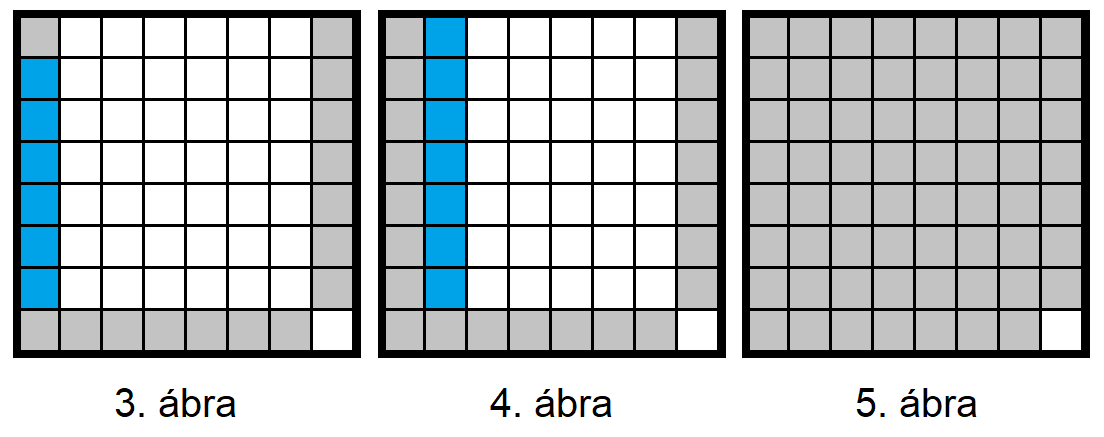
63 bástyát fel tudtunk tenni.
64 bástya nem helyezhető el. Ha a tábla három sarokmezőjén már van bástya, akkor a negyedik sarokba nem tudunk bástyát állítani, mert onnan pontosan kettőt fog eltalálni, függetlenül a többi bástya helyzetétől.
10. Hányféleképp lehet egy 4 x 4-es táblázat mezőiből néhányat pirosra festeni úgy, hogy minden sorban és minden oszlopban páros legyen a befestett mezők száma?
Megoldás. A válasz: 512.
A 4 x 4-es táblának tekintsük a bal felső 3 x 3-as részét. Ebben a részben a 9 mező mindegyikéről szabadon dönthetünk, hogy befestjük vagy sem. Ennek a 9 mezőnek összesen 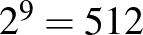 különböző színezése van. Mindegyik színezés egyértelműen befejezhető a 4 x 4-es tábla jobb szélső oszlopának és alsó sorának színezésével úgy, hogy minden sorban és minden oszlopban páros legyen a befestett mezők száma.
különböző színezése van. Mindegyik színezés egyértelműen befejezhető a 4 x 4-es tábla jobb szélső oszlopának és alsó sorának színezésével úgy, hogy minden sorban és minden oszlopban páros legyen a befestett mezők száma.
Ha az első sorban az első 3 mező között páratlan a piros mezők száma, akkor a sorban az utolsó mezőt pirosra festjük; ha pedig páros volt a piros mezők száma, akkor nem festjük be. Ezt megtesszük a tábla első 3 sorában, és hasonlóan járunk el az első 3 oszloppal.
 6. ábra
6. ábraMi lesz a 4 x 4-es tábla jobb alsó mezőjével? Ha az oszlopában fölötte lévő piros mezők száma páratlan, akkor pirosra festjük; míg ha páros, akkor nem festjük be. Ha a tábla utolsó sorát nézzük, akkor a jobb alsó mezőt akkor festjük pirosra, ha abban a sorban az előtt lévő piros mezők száma páratlan. Akár az utolsó oszlopra figyelünk, akár az utolsó sorra, mindkét esetben ugyanazt a választ kapjuk a jobb alsó mező befestéséről. Ugyanis akkor festjük be a jobb alsó sarkot pirosra, ha a bal felső 3 x 3-as részben a piros mezők száma páratlan.
11. Igaz-e a következő állítás? Ha két ugyanakkora kerületű háromszögnek a területe is egyenlő, akkor a két háromszög egybevágó.
Megoldás. A válasz: Az állítás HAMIS.
Legyen az egyik háromszög az 5, 12 és 13 egység oldalhosszú derékszögű háromszög. Ekkor 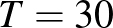 és
és 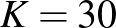 .
.
Zsinegből készítsünk egy 30 egység hosszúságú hurkot. Ha ezt szabályos háromszög alakban feszítjük ki, annak a magassága nagyobb 6-nál. A kifeszített háromszög egyik csúcsát mozgassuk el addig, míg a szemközti oldalhoz tartozó magasság hossza lecsökken 6-ra.
7. ábra
Az így konstruált háromszög területe és kerülete akkora, mint az 5, 12 és 13 oldalú háromszögé ( és
és  ), és ez egy ettől különböző háromszög, hiszen egyik oldala 10 egység.
), és ez egy ettől különböző háromszög, hiszen egyik oldala 10 egység.
12. Felföldön a parlament 40 szenátorból áll, mindegyikük munkáját 3-3 titkár segíti. A 40 szenátor és 120 titkár bizottságokban dolgozik, minden szenátor 6 bizottságnak, és minden titkár 2 bizottságnak a tagja. Egy bizottság vagy 5 szenátorból, vagy 3 szenátorból és 6 titkárból áll. Hány bizottság van összesen?
1. megoldás. A válasz: 64.
Ha minden szenátor kap egy pontot minden bizottságért, amelynek tagja, és minden titkár 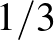 pontot kap minden tagságért, akkor a 40 szenátor összesen 240 pontot, a 120 titkár pedig összesen 80 pontot kap. Ez összesen 320 pont. Másrészt minden bizottságban 5 pontot osztanak szét, tehát
pontot kap minden tagságért, akkor a 40 szenátor összesen 240 pontot, a 120 titkár pedig összesen 80 pontot kap. Ez összesen 320 pont. Másrészt minden bizottságban 5 pontot osztanak szét, tehát 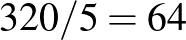 bizottság van.
bizottság van.
2. megoldás.
Az 5 szenátorból álló bizottságok száma legyen 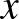 , a vegyes bizottságok száma
, a vegyes bizottságok száma 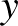 .
.
Olvassuk fel a vegyes bizottságokban részt vevő titkárok neveit, bizottságonként 6 nevet, ez összesen 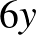 név. Mivel minden titkár két bizottságban vesz részt, így
név. Mivel minden titkár két bizottságban vesz részt, így 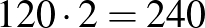 nevet olvasunk fel. Tehát
nevet olvasunk fel. Tehát 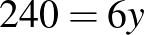 , a vegyes bizottságok száma
, a vegyes bizottságok száma 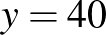 .
.
Most soroljuk fel a bizottságokban résztvevő szenátorok nevét, bizottságonként 5 vagy 3 nevet, ez összesen 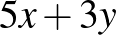 név. Minden szenátor 6 bizottságban vesz részt, ezért most
név. Minden szenátor 6 bizottságban vesz részt, ezért most 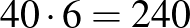 név hangzik el.
név hangzik el. 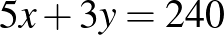 , azaz
, azaz 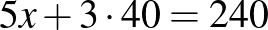 , így
, így 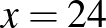 .
.
A bizottságok száma 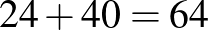 .
.
13. Sandokan és öt kalóza egy asztal körül ülnek, hogy elosszák a zsákmányolt 99 aranyat. Sandokan javaslatot tesz arra, hogy kinek hány arany jusson, ezután az öt kalóz szavaz erről. Egy kalóz igent mond a javaslatra, ha neki több arany jut, mint két szomszédjának összesen. A javaslat szerint osztoznak az aranyon, ha legalább hárman mellette szavaznak. Ha kevesebb a támogató szavazat, akkor Sandokan a szerencsétlen javaslata miatt semmit sem kaphat a zsákmányból. Legfeljebb hány aranyat tud megszerezni Sandokan?
Megoldás. A válasz: 32.
Az első ábrán azt látjuk, hogy Sandokan kaphat 32 érmét, ha két szomszédjának 33-33 aranyat ad, az azok mellett ülő kalózok semmit sem kapnak, míg a Sandokannal szemközi kalóznak 1 arany jut.
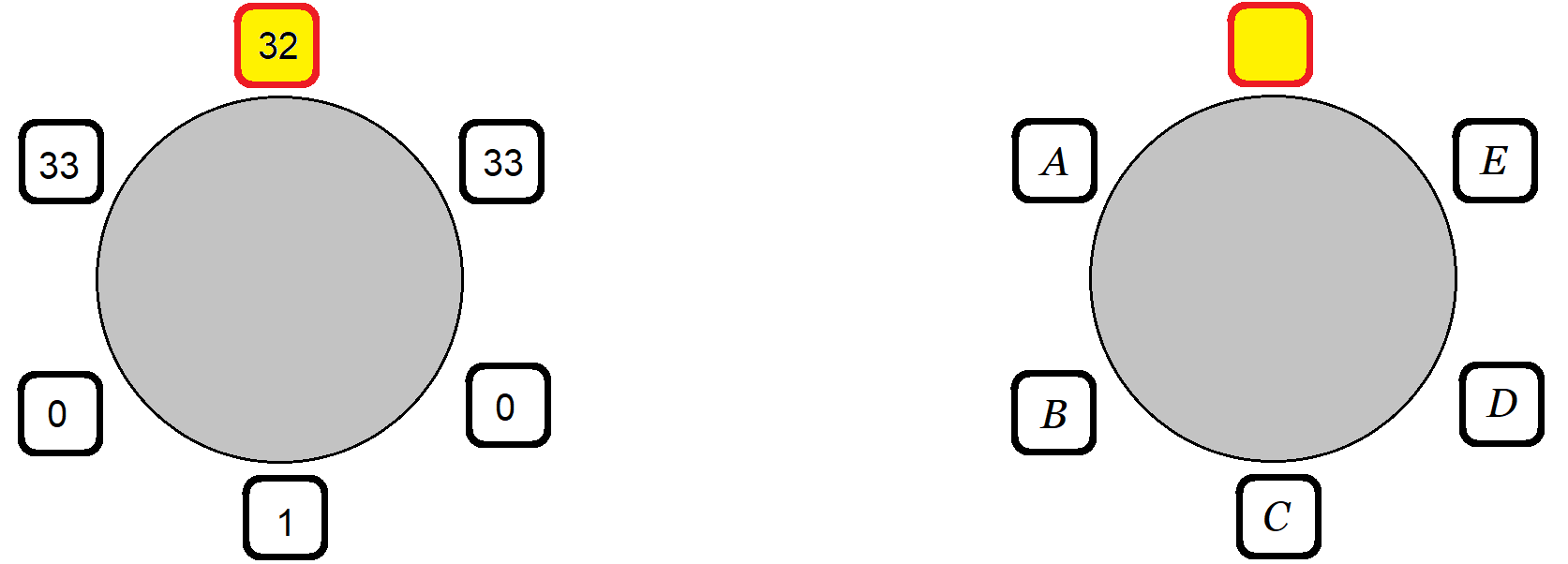
8. ábra
Sandokan nem szerezhet 32-nél több érmét.
Lehetetlen, hogy két szomszédos kalóz mindegyike igennel szavazzon, mivel az igennel szavazó kalóznak több pénzt kell kapnia, mint a szomszédjának.
3 támogató szavazat úgy szerezhető, ha az 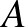 ,
,  ,
, 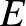 kalózok a javaslat mellett vannak.
kalózok a javaslat mellett vannak.
Ha Sandokan magának legalább 33 érmét ad, akkor az 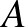 és
és 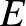 kalózok legalább 34 érmét kapnak, ám ekkor hármójuknak legalább
kalózok legalább 34 érmét kapnak, ám ekkor hármójuknak legalább 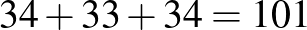 érme jutna, ami nem lehet.
érme jutna, ami nem lehet.
14. Egy tízfős társaság több megbeszélést tartott. Minden egyes találkozón a tíz emberből öten vettek részt. A társaságnak nincs két olyan tagja, akik együtt három megbeszélésen is jelen lettek volna. Legfeljebb hány találkozóra kerülhetett sor?
Megoldás. A válasz: 8.
Ha minden találkozón a résztvevők kezet fognak egymással, akkor egy ember a 9 másikkal összesen legfeljebb 18-szor fog kezet. Egy résztvevő egy találkozón 4 másikkal fog kezet, így legfeljebb 4 találkozón vehet részt, különben legalább 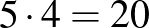 kézfogásban vesz részt, ami 18-nál több.
kézfogásban vesz részt, ami 18-nál több.
A 10 résztvevő legfeljebb 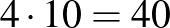 találkozón vesz részt, és így minden találkozót az öt résztvevő miatt 5-ször számolunk, ezért a találkozók száma legfeljebb
találkozón vesz részt, és így minden találkozót az öt résztvevő miatt 5-ször számolunk, ezért a találkozók száma legfeljebb 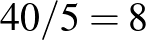 .
.
Lehetséges 8 találkozót szervezni. A 10 résztvevőt jelöljük a 0, 1, 2,  , 9 számokkal. A 8 találkozó résztvevői: 02345, 06789, 02479, 03568, 12376, 13487, 14598, 15269.
, 9 számokkal. A 8 találkozó résztvevői: 02345, 06789, 02479, 03568, 12376, 13487, 14598, 15269.
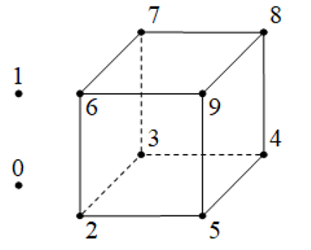
9. ábra
Ha a 2, 3,  , 9 számokat az ábra szerint egy kocka csúcsaiba helyezzük, akkor az előbbi találkozókat tudjuk szemléltetni. A 0 és az 1 kiegészül a kocka valamelyik lapjával (ez 6 lehetőség), vagy négy olyan csúccsal, melyek között nincs kettő, amit él köt össze (ez 2 lehetőség, 2 tetraédert adunk meg ezekkel a pontokkal). Két szomszédos csúcs együtt két lapra illeszkedik, két nemszomszédos csúcs együtt egy lapon és egy tetraéderen szerepelnek. Azaz, a négyesekben előforduló számpárok mindegyikét legfeljebb két négyesben láthatjuk együtt. Ezeket a négyeseket úgy egészítettük ki a 0-val, illetve az 1-gyel, hogy ezek a kocka egy-egy csúcsával legfeljebb kétszer kerülnek közös csoportba.
, 9 számokat az ábra szerint egy kocka csúcsaiba helyezzük, akkor az előbbi találkozókat tudjuk szemléltetni. A 0 és az 1 kiegészül a kocka valamelyik lapjával (ez 6 lehetőség), vagy négy olyan csúccsal, melyek között nincs kettő, amit él köt össze (ez 2 lehetőség, 2 tetraédert adunk meg ezekkel a pontokkal). Két szomszédos csúcs együtt két lapra illeszkedik, két nemszomszédos csúcs együtt egy lapon és egy tetraéderen szerepelnek. Azaz, a négyesekben előforduló számpárok mindegyikét legfeljebb két négyesben láthatjuk együtt. Ezeket a négyeseket úgy egészítettük ki a 0-val, illetve az 1-gyel, hogy ezek a kocka egy-egy csúcsával legfeljebb kétszer kerülnek közös csoportba.











