Érmegráfok

Az Érintő 2023 júniusi számában megjelent Héttusa rovat második feladata így szólt:

2. Egy asztallapra 11 egybevágó fehér korongot helyeztünk úgy, hogy a korongok között nincs átfedés. Igaz-e, hogy a korongokat mindig kiszínezhetjük 3 színnel úgy, hogy az egymással érintkező korongok különböző színűek?

Na, gondoltam, ha így meg van adva, hogy 11, akkor biztos „nem” a válasz, ez remek példa lesz a tízéves lányomnak, könnyen el tudom neki magyarázni az egészet, aztán csak kicsit tologat 11 korongot és biztos hamar rá is bukkan a megoldásra. Szépen le is ültettem 11 koronggal, én meg elkezdtem mást csinálni.

– Apa, túl nehéz! – jött fél óra múlva a nyafogás.

– Persze, mert biztos folyton elábrándozol, és nem is ezen töröd a fejed! – mondtam, és odaültem megmutatni neki, hogyan kell ezt megcsinálni. Aztán elkezdtem izzadni, mert hiába tologattam egyre ingerültebben azokat a korongokat, csak nem találtam meg a megoldást...

Megpróbáltam összeszedni a tudásom, elvégre a kombinatorikus geometria a szakterületem, ez a kérdés pedig pont oda tartozik. A korongok megfeleltethetők egy gráf csúcsainak, melynek az élei az egymással érintkező korongoknak felelnek meg. Mit is tudok erről? Egyrészt világos, hogy ez egy síkgráf, azaz olyan gráf, amely síkbarajzolható anélkül, hogy az élei metszenék egymást. A híres négyszín-tétel szerint egy síkgráf csúcsai mindig kiszínezhetők 4 színnel úgy, hogy semelyik két szomszédos csúcs ne kapjon azonos színt, azaz a kromatikus számuk legfeljebb 4. Tehát ha a feladat 4 színnel lenne feladva, akkor igaz lenne. De vajon tudunk-e minden síkgráfot érintkező korongokkal reprezentálni? A Koebe–Andreev–Thurston-féle körpakolási tétel pont ezt mondja ki, csakhogy ott különböző sugarúak is lehetnek a korongok. Ez egyébként egy szép eredmény, számos alkalmazással, de nekünk most nem segít. Például a 4 pontú teljes gráf, 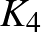 nem reprezentálható egységkorongokkal.

Akkor használjuk azt, hogy minden korong ugyanakkora, mondjuk egységnyi átmérőjű. Ebből kiindulva azt kapjuk, hogy a gráfunknak van egy olyan reprezentációja, amelyben minden csúcsnak egy síkbeli pont felel meg úgy, hogy a szomszédosak távolsága pontosan 1. Az ilyen (nem feltétlenül síkbarajzolható) gráfokat egységtávolsággráfoknak hívják. Ezekről ismert, hogy a kromatikus számuk legfeljebb 7, de azt nem tudjuk, hogy ez az érték éles-e. A legjobb alsó korlát sokáig 4 volt, amit pár éve javított meg de Grey 5-re – erről már írtunk az Érintőben.¹ Azonban amikor ezeket a gráfokat reprezentáljuk egységkorongok érintésgráfjaként úgy, hogy minden csúcsra illesztünk egy korongot, aminek ez a csúcs a középpontja, a korongok tipikusan át fogják egymást fedni, mint például a 4-kromatikus Moser-rokka esetében.

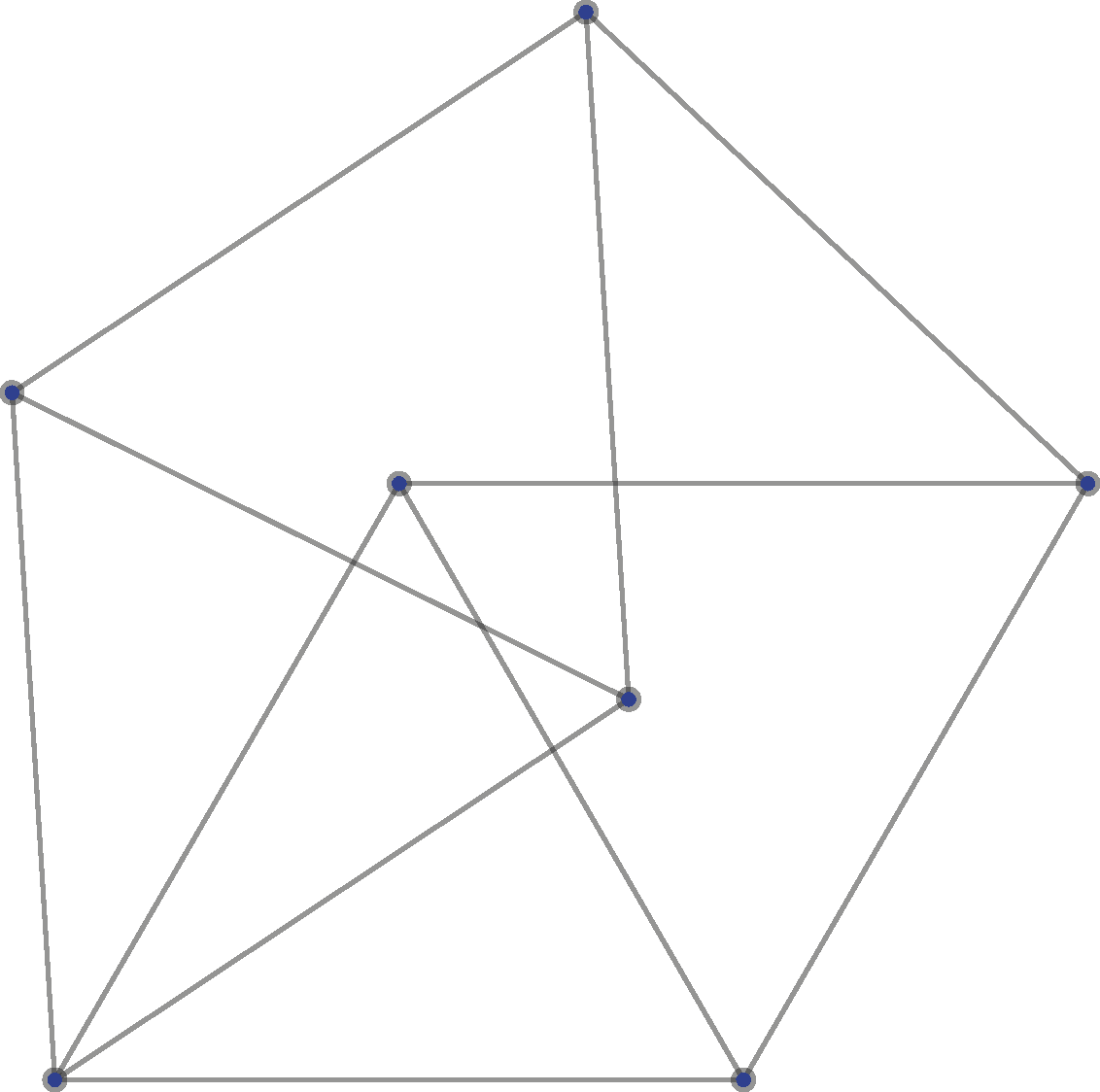
A Moser-rokka

Amikor a csúcsokra illesztett egységkorongok nem fedik át egymást, azaz megfelelnek a feladat feltételeinek, akkor az így kapott gráfot egységérmegráfnak (angolul: penny graph) hívjuk.² Ha különböző méretű érméket is megengednénk, akkor érmegráfokról (angolul: coin graph) beszélnénk, de vigyázat: ha egy egységtávolsággráf érmegráf, attól nem feltétlenül egységérmegráf, hiszen lehet, hogy máshogy kell elhelyezni a csúcsokat a síkon a két reprezentációhoz. Például a Moser-rokka nem egységérmegráf, de érmegráf, hiszen síkba lehet rajzolni, és a fent említett körpakolási tétel miatt a síkgráfok azonosak az érmegráfokkal. Még szintén érdemes megemlíteni a szorosan kapcsolódó gyufagráfokat (angolul: matchstick graph). Ha egy gráf síkbarajzolható úgy, hogy minden éle egység hosszúságú szakasz, akkor hívjuk gyufagráfnak. Ez persze automatikusan teljesül az egységérmegráfokra is, hiszen bármely két érintkező érme középpontja közé rakhatunk egy gyufát. Viszont nem minden gyufagráf lesz egységérmegráf, mert minden csúcsra érmét rakva kaphatunk átfedéseket. Erre a legegyszerűbb példa egy hétágú csillag. Ez természetesen gyufagráf, de nem egységérmegráf, mert abban nem lehetne hatnál nagyobb fokú pont.

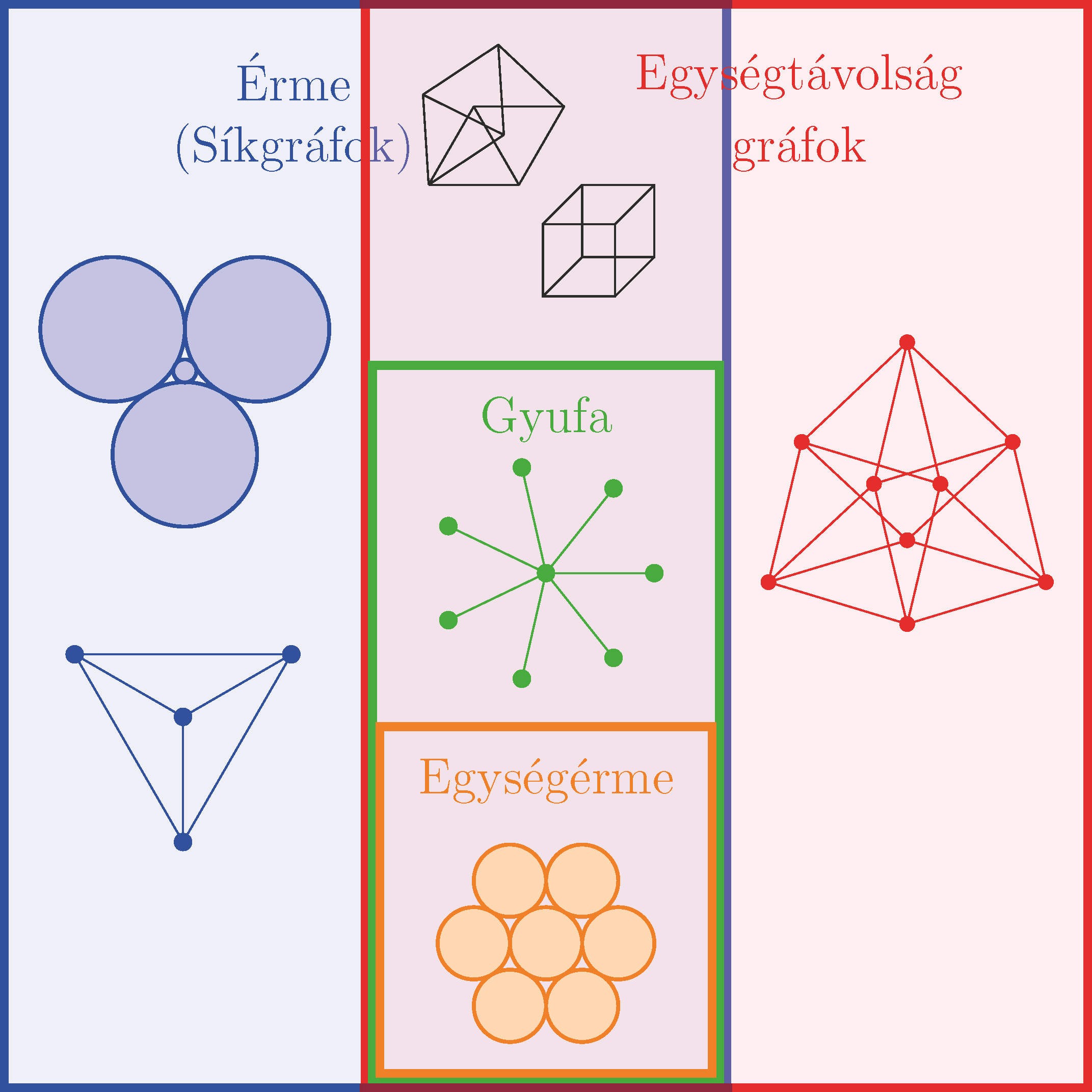
Tehát összefoglalva: A síkgráfok és az érmegráfok ugyanazok. Az egységtávolsággráfok egy másik gráfcsalád. Ennek a két családnak a metszetében vannak a gyufagráfok, és a gyufagráfok részosztálya az egységérmegráfok. Az egységtávolsággráfokat kivéve mindegyik osztályban a maximális kromatikus szám 4, az egységtávolsággráfokról pedig nem tudjuk, hogy 5 és 7 között hol az igazság. Az egységtávolsággráfokról szintén nem tudjuk, hogy mennyi lehet az 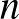csúcsszám függvényében a maximális élszámuk, csak azt, hogy nagyságrendileg 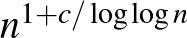és 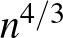között van. Ezzel szemben jól ismert, hogy síkgráfok esetén 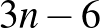, gyufagráfok és egységérmegráfok esetén pedig 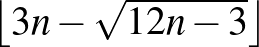a maximális élszám. Ez utóbbi élszám akkor adódik, amikor háromszögrácsszerűen pakoljuk a korongokat úgy, hogy minél kevesebb korong kerüljön a rács szélére. De hiába van sok éle ennek a rácsszerű elrendezésnek, periodikusan háromszínezhető.

Ez sok megoldót félrevezetett, hogy ebből a tömör elrendezésből próbáltak meg kiindulni, és úgy okoskodtak, hogy mivel ez a legsűrűbb, elég erről megmutatni, hogy háromszínezhető. Egy másik tipikus hiba az volt, ha valaki azzal érvelt, hogy mivel nem lehet 4 egymást páronként érintő egységkorong, ezért nincs a gráfban 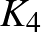, tehát háromszínezhető. Valójában azonban a legnagyobb klikk mérete (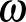) nem felső korlát a kromatikus számra (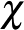); a legismertebb példát erre a Mycielski-gráfok adják.

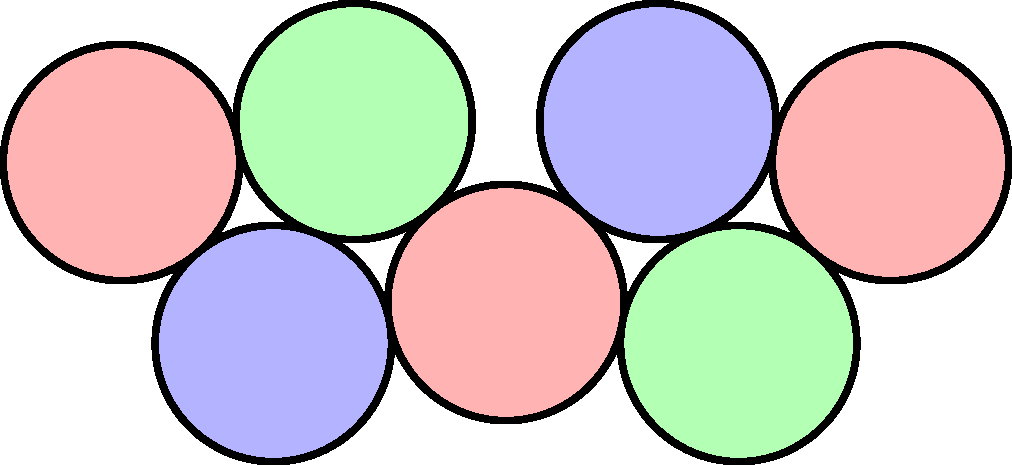Mindenesetre, mivel a legtömörebb elrendezés nem használ, egy olyat kell keresnünk, amiben van egy kis szabadsági fokunk. Hasznos kiindulás, ha veszünk négy korongot rombusz alakzatban elhelyezve; ez 5 érintést ad és garantálja, hogy a két egymást nem érintő korongnak ugyanolyan színűnek kell lennie egy háromszínezésben. Két ilyen rombuszt össze is kapcsolhatunk egy-egy korongjukat azonosítva, és egymáshoz képest el is forgathatjuk őket, mint a bal oldali ábra mutatja. Az ábrán pirossal jelölt korongok szükségszerűen azonos színűek (azonban a kék és zöld színű szomszédos korongok színei mindig felcserélhetőek, de ez nem fontos számunkra).

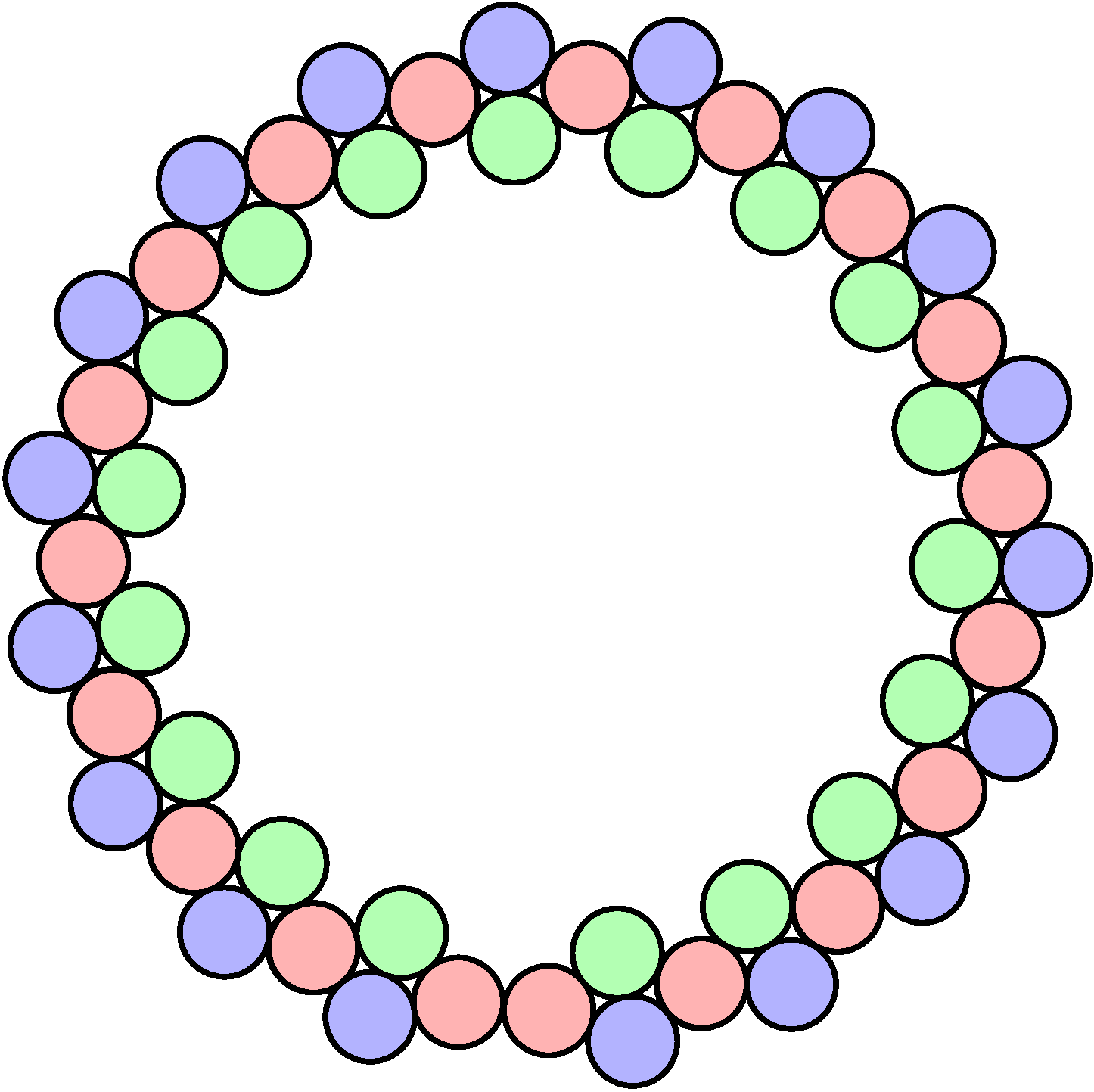Ha elég sok rombuszt összekapcsolunk így sorban, akkor alkalmasan választva a sugarat és a rombuszok közti elforgatásokat, bezárhatunk ezekkel egy kört úgy, hogy az utolsó rombusz jobb oldali korongja pont érintse az első rombusz bal oldali korongját, mint a jobb oldali ábrán látható. Mivel mindkét korong szükségszerűen piros kellene, hogy legyen egy háromszínezésben, ezzel ellentmondásra jutottunk, tehát nem létezhet háromszínezés.³ Ezzel majdnem meg is oldottuk a feladatunk, az egyetlen probléma, hogy jóval több, mint 11 korongot használtunk.

Én itt a magam részéről feladtam, és inkább rákerestem az interneten, hogy mi is a megoldás. Könnyen meg is találtam, sőt, kiderült, hogy ez a természetes kérdés sok emberben felmerült, és számos, egymástól független forrásban⁴ is megtalálható ugyanaz a megoldás, mely egyedi és minimális; a kevesebb korongból álló egységérmegráfok mind háromszínezhetők még.

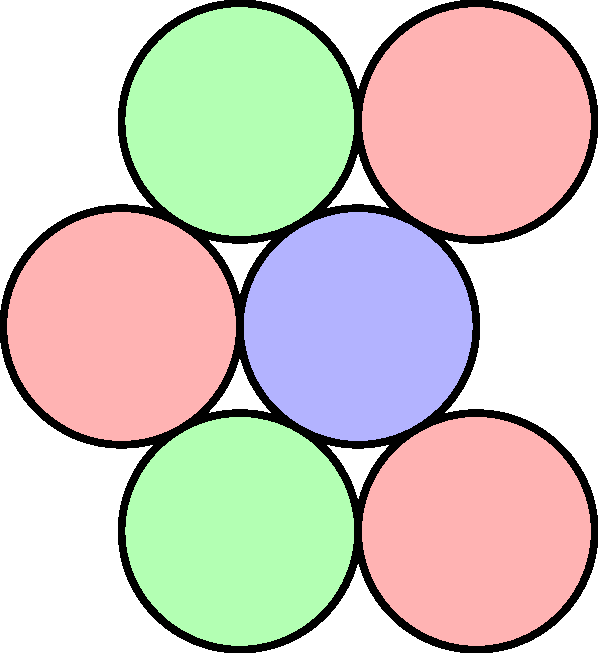Ez is hasonló ötleten alapul, mint a rombuszos, csak itt egy kicsit nagyobb, hat korongból álló alakzatból kell kiindulni (lásd balra). Vegyük észre, hogy itt is igaz, hogy a pirossal jelölt korongok szükségszerűen azonos színűek. Ennek az alakzatnak az az előnye a rombuszoshoz képest, hogy a piros korongok ugyanarra lógnak ki. Így egyetlen elforgatás (vagy akár tükrözés) elég hozzá, hogy két példányt csináljunk belőle, ahol két piros korong egybeesik, két másik pedig érinti egymást, ami igazolja, hogy nem létezhet háromszínezés.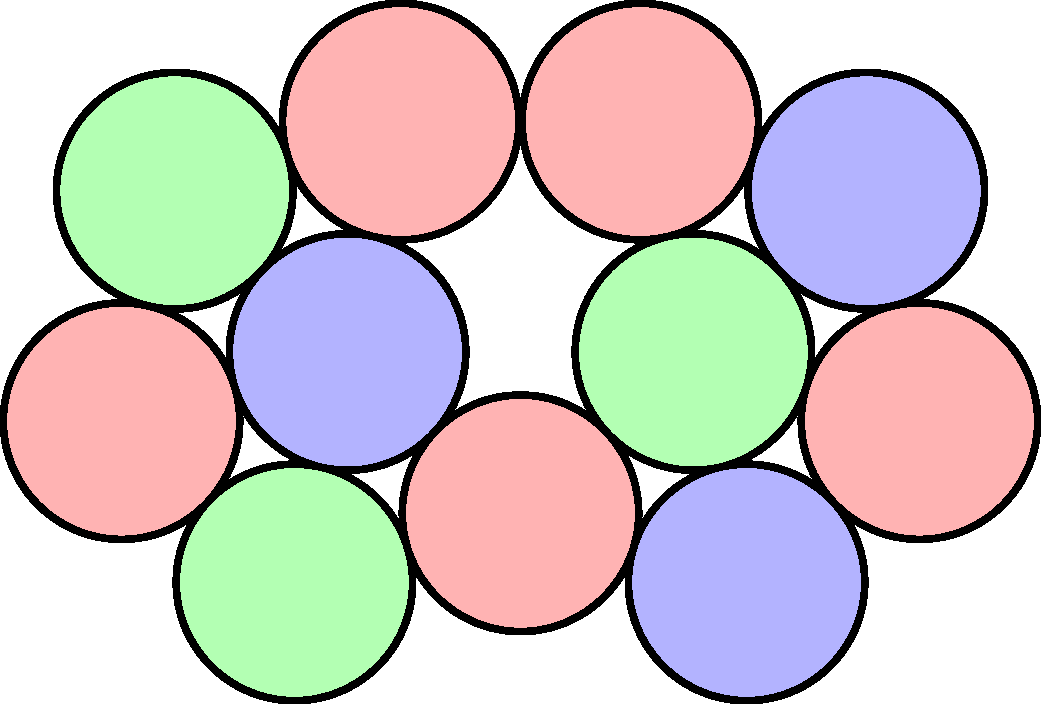

Kapcsolódó érdekességként még két dolgot szeretnék megemlíteni. Az egyik az ún. Ringel-sejtés 1959-ből, amit két éve oldottak meg. Itt azt kérdezte Ringel, hogy ha adott a síkon körök egy rendszere, amelyek átfedhetik egymást, de semelyik három nem megy át egy ponton, akkor az érintési gráfjuk kromatikus számára adható-e felső korlát. Azt sejtette, hogy 5 szín is mindig elegendő lehet, de kiderült, hogy nincs felső korlát, még abban az esetben sem, ha csak egymást kívülről érinthetik a körök és az érintési gráfban nincs 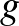-nél rövidebb (gráfelméleti) kör, tetszőleges 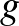-re.⁵

A másik érdekesség pedig, hogy az ember úgy érzi, hogy az ilyen típusú feladatok a játékos matematika körébe tartoznak, és nemigen vannak alkalmazásaik. Legnagyobb meglepetésemre nemrég kiderült, hogy ilyen típusú kérdések még a kvantummechanikában is előjönnek. Tekintsük a következő kérdést. Ki lehet-e három színnel színezni a tér összes vektorát úgy, hogy az egymással derékszöget bezárók mindig különböző színt kapjanak? (Ekvivalensen úgy is feltehetnénk a kérdést, hogy az 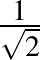sugarú gömbön mekkora lehet egy egységtávolsággráf kromatikus száma.) Az könnyen látható, hogy két szín nem elég, hiszen van három, egymásra kölcsönösen merőleges vektor, azaz háromszög a gráfban. Ha lenne háromszínezés, akkor bármely színosztály vektoraira igaz lenne, hogy semelyik két kiválasztott vektor nem merőleges egymásra, de bármely három, egymásra kölcsönösen merőleges vektor közül valamelyik ki van választva. Nos, az a helyzet, hogy a fentihez hasonló, de valamivel bonyolultabb konstrukcióval meg lehet mutatni, hogy nem létezhet az előző mondat követelményeit teljesítő vektorrendszer. De ami meglepőbb, hogy ebből következik a Kochen–Specker-tétel, mely szerint a kvantumvilágban a mérések nem mindig leírhatók klasszikus értelemben vett állapotokkal, pontosabban a kvantummechanika jóslatai ellentmondanak annak a hipotézisnek, hogy a fizikai mérési statisztikák leírhatóak (klasszikus, potenciálisan korrelált) valószínűségi változókkal. Tehát kis csúsztatással mondhatjuk, hogy az ilyen gráfok színezhetőségétől függ a fizikai valóságunk megismerhetősége!

Lábjegyzetek

¹ https://ematlap.hu/index.php/tudomany-tortenet-2018-09/765-a-sik-kromatikus-szama-mi-tortent-az-elmult-par-honapban-es-mi-tortenhet-meg.

² Legalábbis a Wikipédia szerint, ahol a szócikk legtetején egyből az a kép van, mely tartalmazza a mi feladatunkra a megoldást. Egyébként érdekes, hogy az angolon kívül jelenleg csak két nyelven létezik ez a szócikk, magyarul és perzsául. Mindenesetre sajnos elég nehéz a penny-t magyarra fordítani, mert nekünk nemigen van olyan érménk, aminek külön neve lenne. Pár éve még talán lehetett volna Bélás-gráf :-)

³ Megjegyezzük, hogy a Moser-rokka háromszínezhetetlensége is gyakorlatilag ugyanezen a gondolaton alapul, csak ott egyetlen elforgatás is elegendő.

⁴ Például lásd . 

⁵ Hivatkozás: James Davies, Chaya Keller, Linda Kleist, Shakhar Smorodinsky, Bartosz Walczak: A solution to Ringel's circle problem https://arxiv.org/abs/2112.05042.