A sík kromatikus száma

Mi történt az elmúlt pár hónapban és mi történhet még? 

Pár hónappal ezelőtt, áprilisban, egy biológus, Aubrey de Grey (képünkön) meglepő című cikket [6] töltött fel az ArXivra¹: „The chromatic number of the plane is at least 5”, azaz „A sík kromatikus száma legalább 5”. Tehát ha ki szeretnénk színezni a sík összes pontját úgy, hogy az egymástól pontosan egységtávolságra lévők különböző színt kapjanak, legalább öt színt kell használnunk.

Általánosabban, azt mondjuk, hogy egy gráf kiszínezhető színnel, ha minden csúcsot ki lehet színezni adott szín valamelyikével úgy, hogy azonos színű csúcsok között nem vezet él. Egy gráf kromatikus száma a minimális színszám, amellyel kiszínezhető. Ezt adott gráfra -vel jelöljük. Egy egységtávolság-gráf a síkon egy olyan gráf, amelynek csúcsai pontok a síkon, és két csúcs között akkor és csak akkor megy él, ha pontosan 1 a távolságuk. A sík kromatikus száma, amelyet mostantól -tel jelölünk, nem más, mint annak a (végtelen nagy) egységtávolság-gráfnak a kromatikus száma, amelynek csúcshalmaza az egész sík. Nyilvánvaló, hogy ha a sík kiszínezhető színnel, akkor bármely véges egységtávolság-gráf is. De Bruijn és Erdős tétele szerint a kiválasztási axióma feltételezése mellett ennek a megfordítása is igaz, azaz ha minden véges egységtávolság-gráf kiszínezhető színnel, akkor az egész sík is. Tehát meghatározásához elég véges egységtávolság-gráfokat tanulmányozni.

pontos értékének meghatározása, amelyre Hadwiger–Nelson problémaként szokás hivatkozni, egy több mint 60 éve nyitott kérdés. Klasszikus eredmény, hogy , ezt mutatják az alábbi ábrák. Ezen korlátok belátása jó bemelegítő feladat egy bevezető kombinatorika kurzuson, azonban bármelyiken javítani meglepően nehéz. A kérdés megfogalmazásának egyszerűsége és szépsége miatt könnyen fel szokta kelteni akár műkedvelő, amatőr matematikusok figyelmét is. Más klasszikus, hosszú ideje megoldatlan problémákhoz hasonlóan, időről időre megjelennek félkomoly próbálkozások valamelyik korlát javítására, ám ezekben legtöbbször azonnal kiszúrható hibák vannak.

Két klasszikus példa: Balra a Moser-rokka (Moser 1961 [22]), egy 7-csúcsú 4-kromatikus egységtávolság-gráf, jobbra pedig egy 1-távolságmentes 7-színezés (Isbell 1950, Hadwiger 1961 [14]), amelyben a szabályos hatszögek oldalhossza bármilyen és közötti érték lehet.

Éppen ezért természetes volt a gerontológus de Grey cikkét némi szkepticizmussal fogadni, de ez esetben alaptalanul. De Grey talált egy 1581 pontú példát, amelyhez kell legalább 5 szín, és ezt számítógéppel ellenőrizte. Az eredmény komolyabb érdeklődést váltott ki a témával foglalkozók és a laikusok körében is. Noam Elkies és de Grey indítványozására ún. Polymath projekt indult a témáról, többek között Terence Tao aktív részvételével. (Erről később írunk részletesebben.)

A Hadwiger–Nelson probléma történetéről, kapcsolódó kérdésekről és az új eredményekről Alexander Soifer írt nemrég egy összefoglalót [33], amelynek rövidített verziója online is elérhető. Mi csak annyit említenénk meg, hogy a probléma valójában Edward Nelson kérdése 1950-ből, aki egyből meg is mutatta, hogy 3 szín nem elegendő, míg a 7-es felső korlát John Isbell nevű barátjához fűződik. Soifer könyve [32] tartalmaz sok egyéb érdekességet és kapcsolódó eredményt is. Egy másik, rövidebb összefoglaló található Pach János cikkében [24].

Habár 1950 óta de Grey előtt senkinek nem sikerült -re a triviálisnál jobb korlátokat adni, különböző megszorítások mellett több is ismert volt a sík kromatikus számáról. A racionális koordinátájú pontokról például könnyen megmutatható, hogy 2-színezhetőek, azaz, az eddigi jelölésünket használva, [39]. Ismert volt az is, hogy ha a sík színezéséről megköveteljük, hogy az összes színosztály mérhető legyen, akkor legalább 5 színt kell használnunk [11]. Ennél szigorúbb feltételt kapunk, ha olyan színezést keresünk, amelyben a sík felbontható Jordan-görbék által határolt egyszínű tartományokra. Townsend [38], Woodall [39] picit hibás bizonyításának javításával belátta, hogy ilyen feltételek mellett kell legalább 6 szín. Thomassen megmutatta [37], hogy ha a feltételeket tovább erősítjük úgy, hogy bármely egyszínű tartomány lezártjának átmérője szigorúan kisebb, mint 1, és bármely két, egyszínű tartomány távolsága legalább 1, akkor kell legalább 7 szín. (Megjegyezzük, hogy ilyen feltételek mellett már egy egyenes színezéséhez is 3 szín kell 2 helyett.) Ezek az eredmények azt mutatják, hogy ha van a síknak kevés színt használó színezése, akkor az valamilyen értelemben „csúnya”.

De Grey cikke

De Grey cikkében először a háromszögrács lehetséges 4-színezéseinek egyszerű vizsgálatával megmutatta, hogy a sík bármelyik 4-színezésben található egy oldalú szabályos háromszög csupa egyszínű csúccsal. A bizonyitás a Moser-rokkához hasonlóan egy (nagyobb) háromszögrács ügyes elforgatásaival konstruált egységtávolság-gráf lehetséges színezéseinek vizsgálatán alapult. Ezután egy számítógépes programmal ellenőrizte egy (megfelelő intuícióval konstruált) 1345 csúcsú egységtávolság-gráfról, hogy nincs olyan 4-színezése, amelyben egy bizonyos oldalú szabályos háromszög csúcsai mind egyszínűek.

Hogy a módszer lényegét szemléltessük, adunk egy másik (Hadwiger eredeti [14] bizonyításához hasonló) bizonyítást arra, hogy . Előszőr is megmutatjuk, hogy van két különböző színű pont, amiknek a távolsága pontosan . Ellenkező esetben ugyanis bármely oldalhosszúságú egyenlő szárú háromszögnek mindhárom csúcsa azonos színű lenne, azaz találnánk két azonos színű pontot egymástól 1 távolságra. Tehát vegyünk két pontot, -t és -t, amik egymástól távol vannak és különböző színűek. Jelöljük azt a két pontot amik mind -tól, mind -től 1 távolságra vannak, -rel és -sel. Ekkor, mivel és távolsága is 1, a négyes pontjai páronként különböző színűek, tehát 3 szín nem elég a színezésükhöz.

A de Grey által konstruált első 5-kromatikus gráf, amely háromszögrácsok és a fent említett 1345 csúcsú egységtávolság-gráf Minkowski-összegeként állt elő, 20 425 csúcsú volt. Ezt egy mohó számítógépes eliminációval sikerült 1581-re csökkentenie, amely a Polymath projekt indulásáig a rekord volt.

Polymath project

De Grey cikke után egy ún. Polymath projekt indult a témában, mintegy 50 kutató részvételével. A Polymath projektekben az új részeredmények, ötletek és kérdések a hagyományos cikk-formátum helyett egy internetes blog hozzászólásaiként jelennek meg, kis egységekben és gyors átfutási idővel. A fontosabb részeredmények a projekt Wiki oldalára is felkerülnek a könnyebb visszakereshetőség végett. Az első, Timothy Gowers által 2009-ben indított Polymath projekt célja egy új bizonyítás keresése volt a Hales-Jewett tétel sűrűségi változatára, amely végül az Annals of Mathematicsban jelent meg [26].

A szóbanforgó Polymath projekt egyik célja minél kisebb 5-kromatikus egységtávolság-gráfok keresése volt. Az eredeti 1581 csúcsú példa több lépésben, főleg Marijn Heule közreműködésének köszönhetően 553 csúcsúra csökkent. (A lenti képen egy szimmetrikusabb, 610 csúcsú gráf látható.) Heule módszerének lényege, hogy a színezési feladatot visszavezetjük Boole-formulák kielégíthetőségére, majd egy erre a célra kifejlesztett programmal beazonosítjuk a fölösleges klózokat, és a hozzájuk tartozó csúcsokat elhagyjuk a gráfból. Egy érdekes kérdés, hogy mennyire csökkenthető le a csúcsszám. Pritikin [27] adott egy periodikus 7-színezést, ahol az egyik színosztály sokkal „kisebb”, mint a többi, és ebből levezette, hogy minden legfeljebb 6197 (azóta a Polymath projekt keretében ez 6906-ra javult) csúcsú egységtávolság-gráf 6-színezhető, de a 4-színezhetőséget csak legfeljebb 12 csúcsúakra tudta bizonyítani. Valószínűleg mindkét érték igen távol van az optimális csúcsszámtól.

5-kromatikus egységtávolság-gráf 610 csúcson (Marijn Heule)

A projekt egy másik ága olyan ellenpéldákat keresett, amelyek matematikailag minél egyszerűbben jellemezhetők. Ezek legtöbbször egységvektorok szimmetrikus halmazaiból állnak elő Minkowski-összeg- illetve unióképzéssel. Az egységvektorok szögeit úgy érdemes megválasztani, hogy a háromszögrács valamely csúcsát egy tőle 1 távolságra levő pontba forgassák, ezáltal jönnek létre új élek a gráfban. Ennek megfelelően a konstrukciókban az komplex számok jelennek meg, ahol valamely Eisenstein-egész² normája.

Ezek a példák részei egy megfelelően alacsony fokú bővítésének. Az egyik talált 5-kromatikus gráf mutatja, hogy színezéséhez legalább 5 szín szükséges. még 4-kromatikus, de a színezései szépen strukturáltak, Jannis Harder például megfigyelte, hogy a mindig ugyanazt a színt kapja, mint az origó. Azóta azt is tudjuk, hogy ez a gyűrű csak véges sokféleképpen színezhető, amiből további, az előbb említetthez hasonló következtetéseket tudunk levonni. Ezekre egyelőre csak programmal ellenőrizhető bizonyítás létezik. A blog megjegyzéseiben előkerült pár gráf ( további bővítései bizonyos egységgyökökkel), amiknek színezéséhez potenciálisan 6 szín kellhet, ezek azonban túl nagyok ahhoz, hogy akár számítógéppel is ellenőrizni lehessen.

Mind de Grey eredeti bizonyítása, mind Exoo és Ismailescu [10] időközben megjelent független bizonyítása³ olyan segédállításokon alapszik, hogy egy adott mintázat (mint a oldalú szabályos háromszög csupa egyszínű csúccsal) bármelyik 4-színezésben előfordul illetve egyikben sem fordul elő, majd ezekből jutnak ellentmondásra. Terence Tao ötlete alapján ezek átalakíthatók olyan egyenlőtlenségekké, amik annak a valószínűségét becslik alulról vagy felülről, hogy néhány rögzített ponton egy adott mintázat megjelenik-e egy véletlenszerű színezésben. Például sikerült bizonyítani, hogy mindig létezik egy 1 oldalú szabályos hatszög, amelynek csúcsai két színnel vannak színezve (tehát a hatszög két darab egyszínű oldalú szabályos háromszöget tartalmaz), továbbá, hogy bármilyen és 2 közötti távolságra létezik két, egymástól ilyen messze levő azonos színű pont. Számos hasonló valószínűségi becslés jelent meg a Wiki megfelelő aloldalán, amikből egyszer talán egy számítógépmentes bizonyítás is összeállhat.

Mielőtt ismertté vált, hogy a sík kromatikus száma legalább 5, már tudtuk, hogy ha az egyes színosztályok mérhetők, akkor szükség van legalább 5 színre. Falconer [11] bizonyítása többek között azon alapszik, hogy egy egységtávolság-gráf mindig elhelyezhető a síkon úgy, hogy egy rögzített pontja két színosztály határára essen, ezáltal a szomszédai e két szín egyikét sem kaphatják. Erre alapozva a Polymath projekt olyan gráfokat is keresett és talált, amelyek nem színezhetők ki 4 színnel úgy, hogy egy kiválasztott csúcsuk egyszerre két színt is kapjon, azaz ennek a kiválasztott csúcsnak a szomszédainál mindkét szín tiltva legyen. Ezek jóval kisebbek, 24 csúcsú is van köztük, és kézzel ellenőrizhetők. A projekt egyik ága azt vizsgálja, hogy a nem mérhető esetben milyen hasonló feltételezéseket tehetünk, hiszen ezáltal kiküszöbölhető lenne a program használata, valamint segítené jobb alsó korlátok keresését is. A következő bekezdésben vázolunk egy lehetséges ötletet.

Vegyük a lenti ábrán látható 34 csúcsú gráfot, amelyről esetszétválasztással röviden ellenőrizhető, hogy nincs 4-színezése, ha a középső csúcs kétszínű. Itt a kétszínű középső csúcsnak 18 szomszédja van. Mind a 18 szomszéd köré rajzoljunk egy egységsugarú kört, és jelöljük az így kapott 18 körből álló konfigurációt -vel. Ezek a körök mind átmennek a középső csúcson. Ha a sík bármely adott színezésére tudnánk találni -nek egy olyan egybevágó példányát, ahol a körök közös pontja piros, de mindegyik körön szerepel kék pont is, akkor a körök közeppontjai (azaz a középső csúcs szomszédai) nem lehetnének se pirosak, se kékek, tehát ez annak felelne meg, hogy a középső csúcs kétszínű. Egyelőre nem ismert, hogy minden körkonfigurációra garantálhatjuk-e a síknak minden 4 színnel történő színezése esetén ilyen -vel egybevágó konfiguráció létezését. A körök helyett egyenesekkel azonban igaz a megfelelő állítás.

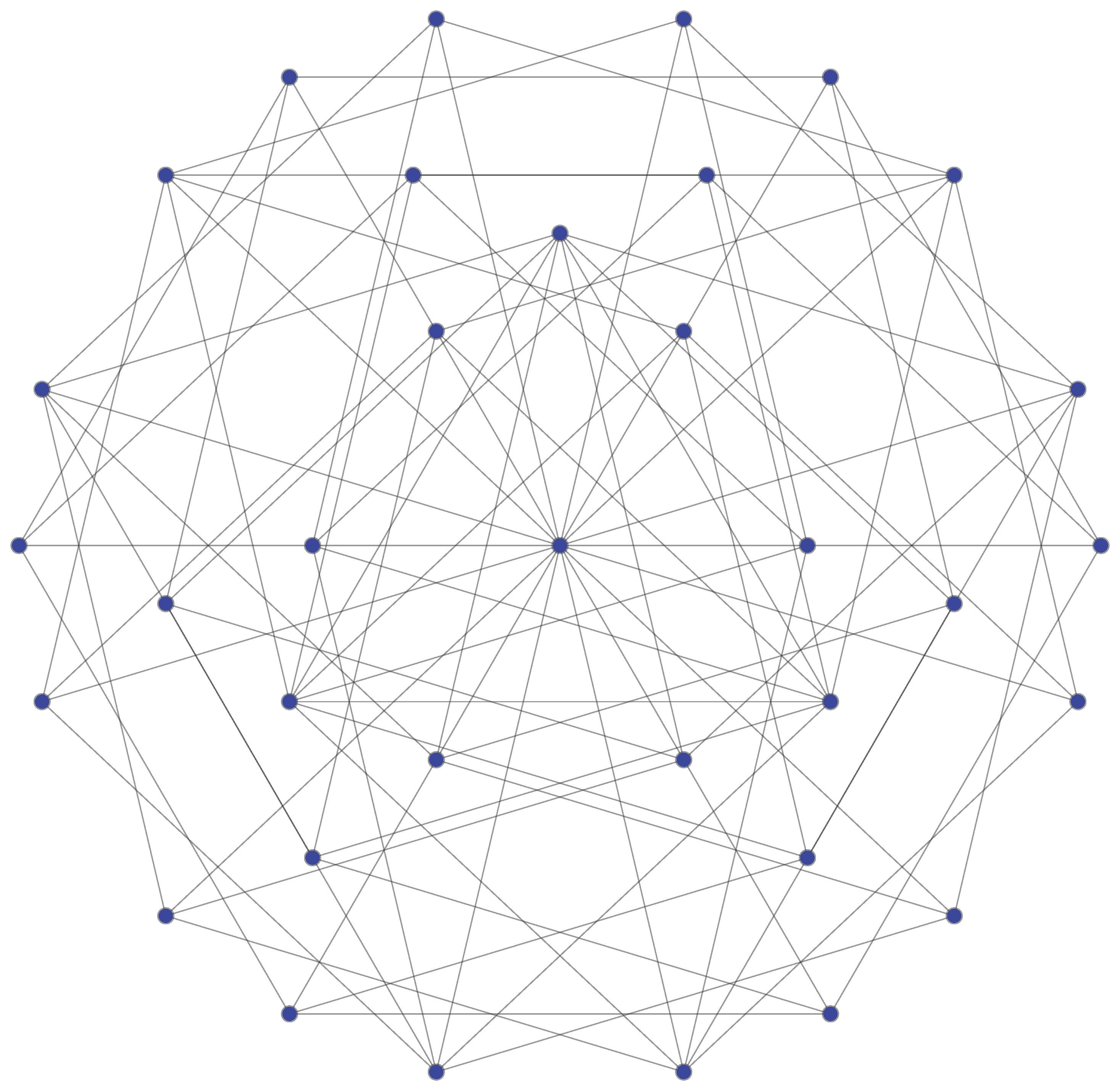
34 csúcsú gráf kétszínű középponttal

Számos más részeredmény is született a Polymath blogon, például periodikus illetve homomorf színezésekről, vagy arról, hogy mekkora körlemezek illetve sávok színezhetők még biztosan 4, 5 vagy 6 színnel.

További változatok, nyitott kérdések

Az eredeti Hadwiger–Nelson probléma rengeteg módon variálható, a témakör tele van izgalmas, megoldatlan kérdésekkel. Kedvcsinálónak az alábbiakban összeszedtünk ezek közül néhányat.

Magasabb dimenzió

Az egyik legtermészetesebb általánosítás a probléma magasabb dimenziós verziója. Mennyi a -dimenziós euklideszi tér kromatikus száma, azaz mennyi ? Itt vizsgálható a kis dimenziós terek kromatikus száma, ismert például, hogy ([4,23,29]). A kis dimenziós esetekre az aktuális legjobb becslésekről egy jó áttekintés Cherkashin, Kulikov és Raigorodskii cikke [3]. Másrészt érdekes aszimptotikus értéke. Ismert, hogy ez egy exponenciális mennyiség, pontosabban [20,31]. Soifer egy merész sejtése, hogy , ha [32].

Egy további kis módosítás: hogyan változik a kromatikus szám, ha megszorítjuk a színezést egy gömbfelületre, azaz mennyi , ahol egy -dimenziós sugarú gömbfelület? Megjegyezzük, hogy ez a mennyiség valóban függ a gömb sugarától. Az ehhez kapcsolódó eredményekről és nyitott kérdésekről egy jó áttekintő Raigorodskii cikke [30].

Több tiltott távolság

A probléma egy további lehetséges általánosítása, ha nem csak azt követeljük meg, hogy az egymástól 1 távol lévő pontok színe különböző legyen, hanem azt is, hogy az 1 helyett ez több különböző távolságra is egyszerre fennálljon. Például ha megtiltjuk hogy azonos színű pontok egymástól 1 vagy 2 távol legyenek, akkor legalább 6 színre [9], míg ha azt tiltjuk meg, hogy az azonos színű pontok egymástól 1 vagy távol legyenek, akkor  legalább 5 színre van szükségünk. Előbbi állításra csak programmal ellenőrizhető bizonyítás ismert, de az utóbbi állításra sikerült „kézzel ellenőrizhető” bizonyítást találni a Polymath projektben. Ez azért érdekes, mert Bukh [2] egy sejtése szerint a kromatikus szám nem nő, ha algebrailag független távolságokat tiltunk meg. Erről csak annyit bizonyított Komjáth és Schmerl [18], hogy ha (akárhány) algebrailag független távolság van tiltva, akkor a kromatikus szám megszámlálható.

Townsend [38] Jordan-görbék által határolt tartományokra vonatkozó eredményének egy egyszerű következménye, hogy ha egy valamely -ra az összes intervallumba eső távolságot megtiltjuk, akkor legalább 6 színre van szükségünk.

Mit mondhatunk a páratlantávolság-gráf kromatikus számáról? Azaz, legalább hány színre van szükségünk, ha úgy akarjuk színezni a sík pontjait, hogy ha két pont távolsága egy páratlan egész szám, akkor azok különböző színűek? Nyilvánvalóan legalább szín kell, és meglepő módon ennél sokkal több nem ismert. Nem tudjuk például, hogy véges-e ez az érték, de tudjuk, hogy mérhető színosztályokkal nem az [1,2,12].

Hiperbolikus sík

Szintén vizsgált a hiperbolikus sík kromatikus száma. Fontos különbség az euklideszihez képest, hogy míg az euklideszi síkon ha az 1 távolságot kicseréljük más fix távolságra, nem változik a kromatikus szám, addig ugyanez nem igaz a hiperbolikus síkon. Mennyi , azaz legalább hány színnel kell színeznünk a hiperbolikus síkot, ha két egymástól távolságra lévő pont nem lehet azonos színű? Ismert, hogy 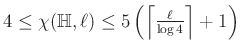[25], de nem világos, hogy van-e -től független felső korlát.

Más normák

Mit mondhatunk az euklideszitől különböző normált terekről? Érdekes megjegyezni, hogy de Grey konstrukciója előtt nem volt ismert, hogy van-e egyáltalán olyan normált sík, amelynek a kromatikus száma legalább 5. A legáltalánosabb alsó és felső korlátok a következők: [19,35], ahol tetszőleges -dimenziós normált tér, de nem nehéz megmutatni, hogy , ahol a -dimenziós tér a max-normával. Az elmúlt hónapokban talált kis csúcsszámú, 5-kromatikus számú gráfok közül vajon melyik ágyazható be -be? Normált terek kromatikus számáról jó áttekintést ad Swanepoel cikke [36].

Egyéb kapcsolódó problémák

Zárásképp megemlítünk néhány egyéb, bizonyos értelemben kapcsolódó problémakört.

Mérhető halmazok esetén természetes kérdés, hogy legfeljebb mekkora lehet egy 1-távolság-mentes halmaz sűrűsége. Erre a legjobb korlátok jelenleg 0.2293 alulról [5] és 0.2588 felülről [17]; ezzel a módszerrel tehát a legjobb elérhető alsó korlát a kromatikus számra (mérhető színezésekre) 4 vagy 5. Hasonlóan nézhetnénk például, hogy a síknak mekkora része 4-színezhető. Erre a legjobb korlátok jelenleg 0.9174 alulról [27] és felülről [15]. (Ez utóbbi egyszerű következménye annak, hogy létezik 553 csúcsú egységtávolság-gráf.)

Erdős egyik ismert kérdésese, az egységtávolságok problémája [8] azt kérdezi, hogy pont a síkon legfeljebb hány egységtávolságot határozhat meg. Másképp, legfeljebb hány éle lehet a síkon egy csúcsú egységtávolság-gráfnak? E híresen nehéz kérdésre a jelenleg ismert legjobb felső korlát, , Spencertől, Szemeréditől és Trottertől származik [34], és messze van a legjobb ismert alsó korláttól, ami egy megfelelő oldalhosszúságú négyzetrácsra . Ebből következik, hogy egy egységtávolság-gráfnak nem lehet túl sok éle, tehát például biztosan nem lesz sűrű gráf. Másrészt egy minimális -kromatikus gráfnak minden csúcsa legalább fokú, tehát legalább éle van.

Egyszínű konfigurációk, mint például egységtávolságra lévő pontok tiltása helyett lehet a célunk adott alakzattal egybevágó monokromatikus halmaz keresése is. Az eredeti, sík kromatikus számára vonatkozó kérdés ezen a nyelven így szólna: Mi az a legnagyobb , amelyre igaz, hogy bárhogy színezzük a síkot színnel, mindig találunk két azonos színű pontot egymástól 1 távolságra? Kicsit tovább variálva, adott -ra mi az a legkisebb dimenzió amelyre igaz, hogy -t bárhogy színezve színnel, mindig találunk két azonos színű pontot egymástól 1 távol. Általában pedig vizsgálhatjuk, hogy adott véges ponthalmazra mi az a legkisebb , hogy -t tetszőlegesen színezve színnel mindig találunk egy egyszínű, -sel egybevágó⁴részhalmazt. Nem minden -re létezik minden -ra; egy szükséges feltétel, hogy egy gömbfelületen helyezkedjen el, és sejtés, hogy ez elégséges is. Az ilyen ponthalmazok karakterizálásáról szól az ún. euklideszi Ramsey-elmélet [7,13,21].

Irodalomjegyzék

[1] Jean Bourgain. A Szemerédi type theorem for sets of positive density in 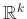. Israel Journal of Mathematics, 54(3):307–316, 1986. 

[2] Boris Bukh. Measurable sets with excluded distances. Geometric and Functional Analysis, 18(3):668–697, 2008. 

[3] Danila Cherkashin, Anatoly Kulikov, and Andrei Raigorodskii. On the chromatic numbers of small-dimensional euclidean spaces. Discrete Applied Mathematics, 243:125–131, 2018. 

[4] David Coulson. A 15-colouring of 3-space omitting distance one. Discrete mathematics, 256(1-2):83–90, 2002. 

[5] H. T. Croft. Incidence incidents. Eureka, 30:22–26, 1967. 

[6] Aubrey D.N.J. de Grey. The chromatic number of the plane is at least 5. Geombinatorics, 28:18–31, 2018. arXiv preprint arXiv:1804.02385. 

[7] P. Erdős, R. L. Graham, P. Montgomery, B. L. Rothschild, J. Spencer, and E.G. Straus. Euclidean Ramsey theorems. I. Journal of Combinatorial Theory, Series A, 14(3):341 – 363, 1973. 

[8] Paul Erdős. On sets of distances of n points. The American Mathematical Monthly, 53(5):248–250, 1946. 

[9] Geoffrey Exoo and Dan Ismailescu. The Hadwiger-Nelson problem with two forbidden distances. Geombinatorics, 28:51–68, 2018. arXiv preprint arXiv:1805.06055. 

[10] Geoffrey Exoo and Dan Ismailescu. The chromatic number of the plane is at least 5 - a new proof. ArXiv e-prints, April 2018. 

[11] Kenneth J. Falconer. The realization of distances in measurable subsets covering rn. Journal of Combinatorial Theory, Series A, 31(2):184–189, 1981. 

[12] Kenneth J. Falconer and John M. Marstrand. Plane sets with positive density at infinity contain all large distances. Bulletin of the London Mathematical Society, 18(5):471–474, 1986. 

[13] Ronald L. Graham. Euclidean ramsey theory. In Jacob E. Goodman and Tóth [16], pages 281–297. 

[14] Hugo Hadwiger. Ungelöste probleme, nr. 11. Elemente der Mathematik, 16:103–104, 1961. 

[15] Marijn J.H. Heule. Computing small unit-distance graphs with chromatic number 5. Geombinatorics, 28:32–50, 2018. arXiv preprint arXiv:1805.12181. 

[16] Joseph O'Rourke Jacob E. Goodman and Csaba D. Tóth, editors. Handbook of Discrete and Computational Geometry, Third Edition. Chapman and Hall/CRC, 2017. 

[17] Tamás Keleti, Máté Matolcsi, Fernando Mário Oliveira Filho, and Imre Z. Ruzsa. Better bounds for planar sets avoiding unit distances. Discrete Comput. Geom., 55(3):642–661, April 2016. 

[18] Péter Komjáth and James Schmerl. Graphs on Euclidean spaces defined using transcendental distances. Mathematika, 58(1):1–9, 2012. 

[19] Andrey Kupavskiy. On the chromatic number of rn with an arbitrary norm. Discrete Mathematics, 311(6):437–440, 2011. 

[20] David G. Larman and C. Ambrose Rogers. The realization of distances within sets in euclidean space. Mathematika, 19(1):1–24, 1972. 

[21] Imre Leader, Paul A. Russell, and Mark Walters. Transitive sets in euclidean ramsey theory. J. Comb. Theory, Ser. A, 119(2):382–396, 2012. 

[22] Leo Moser and William Moser. Solution to problem 10. Can. Math. Bull., 4:187–189, 1961. 

[23] Oren Nechushtan. On the space chromatic number. Discrete mathematics, 256(1-2):499–507, 2002. 

[24] János Pach. Finite point configurations. In Jacob E. Goodman and Tóth [16], pages 3–25. 

[25] Hugo Parlier and Camille Petit. Chromatic numbers for the hyperbolic plane and discrete analogs. arXiv preprint arXiv:1701.08648, 2017. 

[26] D. H. J. Polymath. A new proof of the density Hales-Jewett theorem. Ann. of Math. (2), 175(3):1283–1327, 2012. 

[27] Dan Pritikin. All unit-distance graphs of order 6197 are 6-colorable. Journal of Combinatorial Theory, Series B, 73(2):159 – 163, 1998. 

[28] Richard Rado. Note on combinatorial analysis. Proc. London Math. Soc. (2), 48:122–160, 1943. 

[29] Radoš Radoičić and Géza Tóth. Note on the Chromatic Number of the Space, pages 695–698. Springer Berlin Heidelberg, Berlin, Heidelberg, 2003. 

[30] Andrei M. Raigorodskii. Coloring distance graphs and graphs of diameters. In Thirty essays on geometric graph theory, pages 429–460. Springer, 2013. 

[31] Andrei Mikhailovich Raigorodskii. On the chromatic number of a space. Russian Mathematical Surveys, 55(2):351–352, 2000. 

[32] Alexander Soifer. The Mathematical Coloring Book. Springer-Verlag New York, 2009. 

[33] Alexander Soifer. Progress in my favorite open problem of mathematics, chromatic number of the plane: An Étude in five movements. Geombinatorics, 28:5–17, 2018. Rövidített online verzió. 

[34] Joel Spencer, Endre Szemerédi, and William T Trotter. Unit distances in the euclidean plane. In Graph theory and combinatorics, pages 293–308. Academic Press, 1984. 

[35] Konrad Swanepoel and Rafael Villa. A lower bound for the equilateral number of normed spaces. Proceedings of the American Mathematical Society, 136(1):127–131, 2008. 

[36] Konrad J. Swanepoel. Combinatorial distance geometry in normed spaces. arXiv preprint arXiv:1702.00066, 2017. 

[37] Carsten Thomassen. On the Nelson unit distance coloring problem. The American Mathematical Monthly, 106(9):850–853, 1999. 

[38] S. P. Townsend. Colouring the plane with no monochrome units. Geombinatorics, 14(4):184–193, 2005. 

[39] Douglas R. Woodall. Distances realized by sets covering the plane. Journal of Combinatorial Theory, Series A, 14(2):187–200, 1973.

 

Lábjegyezetek

¹ Ez egy olyan oldal, ahova bárki feltöltheti (lektor által ellenőrizetlenül) a legfrissebb tudományos eredményeit mindenki számára ingyenesen elérhetően. A legtöbb új jelentős matematikai eredmény megtalálható itt.

² Ezek a háromszögrács pontjainak koordinátái, azaz alakú komplex számok, normáik az 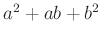alakú számok.

³ Úgy tűnik, hogy ez a szerzőpáros is nagyjából de Greyjel egyidőben bizonyította a tételt, csak lassabbak voltak a nyilvánosságra hozatallal és így lemaradtak a hírnévről.

⁴ Ha egybevágó helyett -hez hasonló egyszínű részhalmazt keresnénk, akkor minden véges -ra találnánk terének dimenziójában Gallai egy tétele szerint [28,32].