Mi is az a ... perzisztens homológia?

Barátom, Partha Niyogi (1967-2010) emlékére

Vessünk egy pillantást Seurat egy képére, vagy egy régi újságra. Szemünk vagy agyunk egyik csodálatos képessége, hogy a különálló pontokból álló adathalmazból egy összefüggő képet – a diszkrétből folytonosat – alkot.

Adatok elemzése során rendszeresen felmerülnek hasonló problémák. A vizsgált minta eloszlása esetleg nem egyenletes, illetve folyton-folyvást meg kell küzdeni a jelenlévő zajjal is: egy adathalmaz sokféleképp torzulhat.

Azonban elméleti matematikusok is találkoznak efféle kihívásokkal. Gyakran előfordul, hogy egy burkoló tér tulajdonságait szeretnénk megismeri egy benne lévő diszkrét objektum segítségével, vagy fordítva: egy adott folytonos objektumhoz rendelt összes diszkét objektum közös tulajdonságait szeretnénk feltárni. Egy példa az utóbbi esetre a geometriai csoportelmélet egy (Fürstenbergtől és Mostowtól származó) tipikus kérdése, hogy miképp tudunk egy összefüggő Lie-csoportot egy benne található rács ismeretében rekonstruálni.

Az analízisben pedig teljesen általános, hogy egy függvény tulajdonságait az őt közelítő függvények alapján próbáljuk megismerni. Például minden, a komplex síkon értelmezett, a $z\mapsto z^n$ függvényhez egyenletesen közel lévő függvénynek (multiplicitással számolva) legalább $n$ gyöke van.

Talán nem meglepő, hogy a topológia – egy lényegében kvalitatív terület – keretein belül átfogó módszer keletkezett a fentiekhez hasonló problémák kezelésére. Természetesen az ilyen problémák megoldásainak legfontosabb értéke alkalmazhatóságuk nagyon különböző aspektusaiban rejlik. A következőkben azonban a bennük lévő hasonlóságokra fogunk fókuszálni. Az egyszerűség kedvéért az alábbiakban minden homológiacsoportot testből vett együtthatókkal tekintünk.

Definíció: Legyen $X=\{ X_r\mid r\in {\mathbb{R}}\}$ (bizonyos enyhe technikai feltételeket teljesítő) tereknek egy, a valós számok ${\mathbb{R}}$ halmazával paraméterezett, egymásba ágyazott sorozata. Az $X$ tér $PH_k(X)$ $k$ -adik perzisztens homológiáját a

$\displaystyle PH_k(X)=\Pi H_k (X_r)$

formulával definiáljuk. A jobb oldalon lévő szorzat alapvetően egy borzasztó objektum: formálisan egy nem megszámlálható dimenziójú vektortér. De van egy ésszerű mód arra, hogy ebből egy kezelhető objektumot kapjunk, amennyiben figyelembe vesszük az $X_r\subset X_s$ ( $r<s$ ) beágyazások által indukált $H_k(X_r) \to H_k(X_s)$ leképezéseket is.

A $H_k(X_r)$ csoport egy elemét véve követhetjük annak útját „tovább az időben” nagyobb $s$ -ekre, és figyelhetjük azt, vajon később meghal-e (vagyis valamikor a csoport nulla-elemébe képződik) vagy sem. Amennyiben $H_k(X_r)$ véges dimenziós, akkor megadható egy bázisa úgy, hogy minden egyes báziselem halálának van egy jól meghatározott pillanata, és a báziselemek egy lineáris kombinációja akkor hal meg $H_k(X_s)$ -ben, ha minden olyan báziselem, amely a lineáris kombinációban nemnulla együtthatóval szerepel, meghal $H_k(X_s)$ -ben. (Ez az állítás könnyen következik elemi lineáris algebrai megfontolásokból.)

Egy $f\colon Z\to {\mathbb{R}}^+$ pozitív valós értékű függvény konkrét példát ad az alábbi módon: tekintsük az $f^{-1}[0,r]$ inverz képeket mint $Z$ közelítéseit. Ez alapján vannak olyan homológiaosztályok, amelyek rögtön $r=0$ -nál „megszületnek”, vagyis benne vannak $H_k(f^{-1}\{ 0\})$ képében, de vannak olyanok is, amelyek csak később születnek meg. Vannak továbbá olyanok, amik később születnek, de valamivel később meg is halnak.²

A fenti képet egy „vonalkóddal” foglalhatjuk össze, amely eltárolja a születéseket és halálokat. Az ábra egy az $S^2$ gömbfelületen értelmezett függvényre mutatja az 0- és 1-dimenziós perzisztens homológiát.

A függvényekkel való megközelítésben a perzisztens homológia a Morse-elmélet egy változatának tekinthető. Egy Morse-függvény minden egyes kritikus pontja vagy egy homológiaosztály születésének hírnöke, vagy egy másik homológiaosztály halálának előszele. Ily módon a kritikus pontok mindig láthatóak a vonalkódban: vagy a kritikus pont indexének dimenziójában, vagy annál eggyel kisebb dimenzióban.

Térjünk most vissza eredeti motiváló példáinkhoz. Vegyük az euklideszi tér egy $M$ részsokaságát (mondjuk egy emberi arcot), mintavételezzünk róla pontokat (pointillista módon), majd tekintsük azt a függvényt, amelynek $f(x)$ érteke egyenlő $x$ -nek a legközelebbi mintaponttól vett távolságával. Ekkor $f$ alsó szinthalmazainak homológiája számítógépes algoritmusok segítségével kiszámolható. Amennyiben $s$ nagyobb, mint a minták sűrűsége, azon a szinten megjelenik $M$ minden homológiája, és ha $s$ nem túl nagy, akkor a kapott homológia egyenlő lesz $M$ homológiájával (bár egy idő után $M$ homológiái meg fognak halni). $PH_1$ számolására egy tipikus példa a kovetkező vonalkód, amelyet a 2-tóruszon felvett 1400 mintapontból kaptunk (és a perzisztencia paramétert a szokásoknak megfelelően vízszintesen ábrázoltuk):

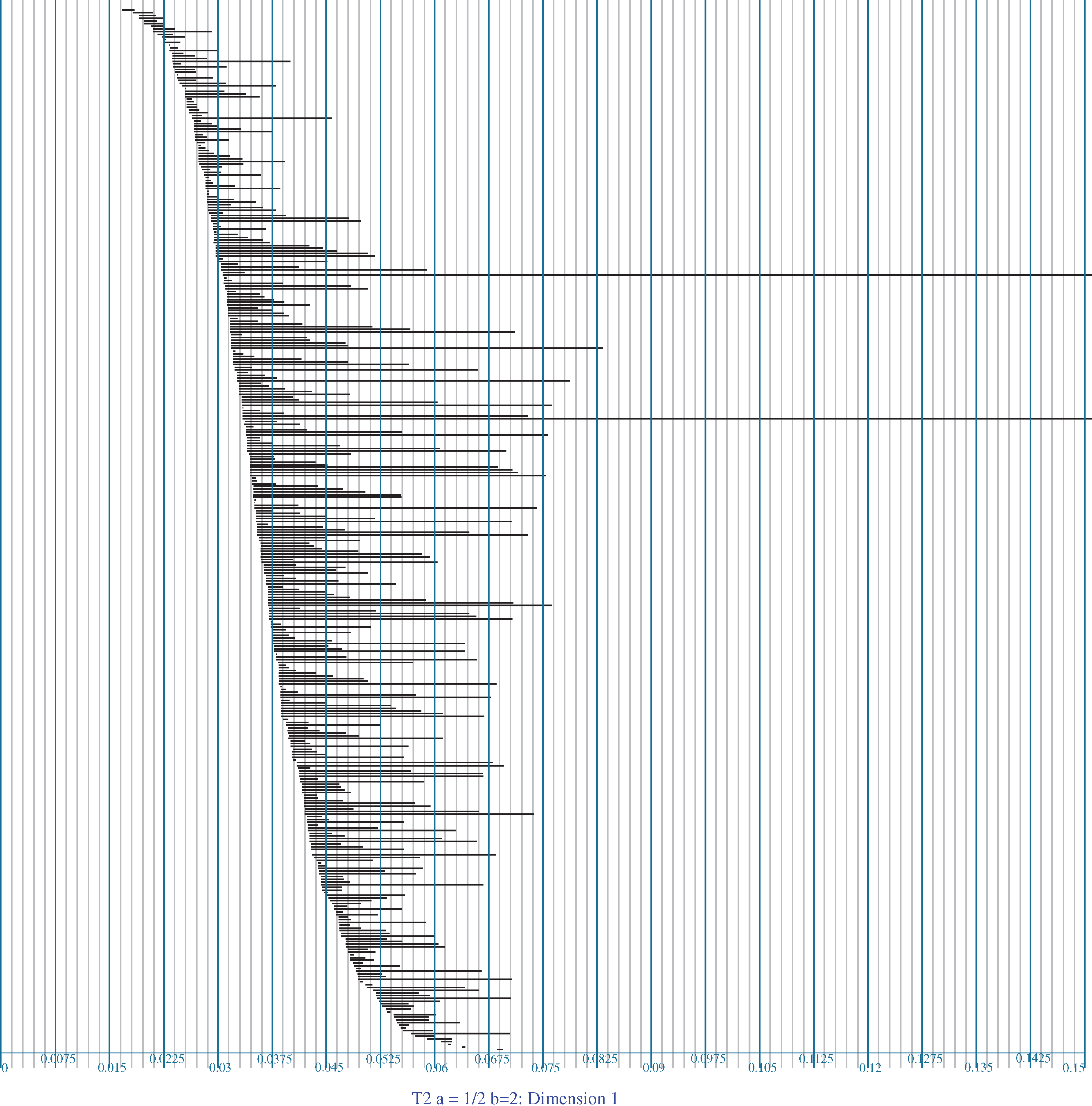
Ebben a példában nincs zaj; a rövid vonalak a választott mintapontok szabálytalanságát és választásunk nem túlságosan magas hatásfokát tükrözik. Még sok minden vár felfedezésre azügyben, hogy mit is jelentenek a vonalkódok alakjai, de már vannak olyan tételek, amelyek megmutatják, hogyan használható a $PH$ objektum a valódi homológiacsoportok kiszámítására akkor, amikor a mintapontok elég sűrűn helyezkednek el, és nem túl nagy a zaj.

Majdnem minden alkalmazásban kulcsszerep jut egy stabilitási tételnek, amely szerint „közeli” függvények (vagy filtrációk) esetén a vonalkódok sem lehetnek egymástól (egy jólmeghatározott kvantitatív értelemben) nagyon messze. A vonalkódok terén lévő topológia szerint két vonalkód akkor van egymáshoz közel, ha a „rövid intervallumokat” elhanyagolva a többi (hosszú) intervallumok megfeleltethetőek egymásnak úgy, hogy végpontjaik egymáshoz közel legyenek. Talán a következő kép elegendő ennek illusztrálására:

„közel” van

a vonalkódhoz, mert a „rövid” intervallumotól eltekintve a két vonalkód összehangolható.

Edelsbrunner, Cohen-Steiner és Harer stabilitási tétele azt mondja ki, hogy ha a függvények egymástól legfeljebb $C$ távolságra vannak, akkor a hosszú vonalak a kódokban megfelelnek egymásnak, vagyis kezdő- és végpontjaik nem mozdulnak el $C$ -nél nagyobb mértékben, míg a rövid, $C$ -nél rövidebb hosszúságú intervallumok tetszőlegesen különbözőek lehetnek. Az olvasó meggyőződhet az $y=x^2$ és az $y=x^2+\sin (1000 x)$ , ${\mathbb{R}}$ -en értelmezett függvények esetében arról, hogy a fenti tétel miért is áll fenn.

Amikor a fenti ötleteket egy, a szó-metrikával ellátott csoportra alkalmazzuk, egy másfajta egymásba ágyazott térsorozatot képezünk.³

Ezek a terek mind szimpliciális komplexusok. $r>1$ esetén az $r$ -hez rendelt tér $k$ -szimplexei csoportelemek olyan $(k+1)$ -eseiből állnak, amelyek páronként legfeljebb $\log (r)$ távolságra vannak.

Nem nehéz belátni, hogy más-más generátorrendszer vagy ugyanazon Lie-csoport más-más rácsai esetén ezek a szimpliciális komplexusok egymáshoz közel vannak (távolságuk lényegében az egyik generátorrendszer elemeit a másikban felíró szavak hosszától függ), így az eredményül kapott perzisztens homológiák is nagyon közeliek. Ezt az eredményt arra lehet például használni, hogy megmutassuk, csoportok bizonyos homologikus tulajdonságai csak a „durva kvázi-izometria típustól” függnek, és megegyeznek egy adott Lie-csoport különböző uniform rácsaira. Egy, lényegében Gersten-től származó példa szerint, az utolsó olyan dimenzió, amiben a perzisztens homológiában hosszú (vagyis végtelen hosszú) intervallum jelenik meg, meghatározza a kohomológikus dimenziót.

Utolsó példánkhoz vegyünk egy $M$ Riemann-sokaságot. Terünk az $X = \Lambda M=\{\gamma \colon S^1\to M\}$ tér lesz, $M$ sima hurkainak tere. Függvényünket pedig a „log energia” függvény adja:

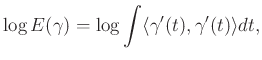
$\displaystyle \log E(\gamma ) =\log \int \langle \gamma ' (t), \gamma ' (t)\rangle dt,$

ahol $\langle \cdot , \cdot \rangle$ a Riemann-struktúra által adott belső szorzás. Vegyük észre, hogy bár a log energia függ a választott Riemann-metrikától, két különböző metrikára ugyanazon a sokaságon a függvények különbsége korlátos. Ennek következménye, hogy a stabilitási tétel miatt ezen huroktér perzisztens homológiája – véges távolság erejéig – a sokaság egy invariánsa, vagyis a metrikától független. A következő, lényegében Gromovtól származó eredmény bizonyítása már majdnem következik a fentiekből:

Tétel: Legyen $M$ egy kompakt Riemann-sokaság. Az a tulajdonság, hogy van egy olyan univerzális $C$ konstans, amelyre minden $L$ hosszú zárt homotopikusan triviális geodetikus pontrahúzható legfeljebb $CL$ hosszú geodetikusokon keresztül, egy $M$ metrikájától független tulajdonság. Valójában ez csak $M$ fundamentális csoportától függ. Ez a tulajdonság továbbá ekvivalens avval, hogy nincsenek tetszőlegesen hosszú intervallumok a $\Lambda M$ -beli konstans hurkok komponensének $PH_0$ perzisztens homológiájában.

Az utolsó mondat rögtön megmagyarázza az azt megelőzőt. A geodetikusokra vonatkozó geometriai feltétel csak a fundamentális csoporttól függ (és nem a sokaságtól), mivel ez teljesül (majdhogynem definíció szerint) a hurkok 0-dimenziós homológiájára. Olyan véges csoportok, amelyeknek nem megoldható a szó-problémája, példákat adnak olyan csoportokra, amelyekre a feltételek nem teljesülnek (mivel a perzisztens intervallumok hosszára adott felső becslés egy, a szó-problémát megoldó algoritmust adna). Az ilyen fundamentális csoportú sokaságokra a tétel sok érdekes homotopikusan triviális geodetikus létezését adja. A témáról továbbiakat találhatunk Alex Nabutovsky-nak a 2010-es ICM kongresszuson tartott előadásában.

A perzisztens homológia fogalmi rendszere alkalmazott matematikának is tekinthető. Az alkalmazott matematika igényei ugyanis olyan szótárat adtak a kezünkbe, amellyel kényelmesen kifejhetők bizonyos, az elméleti matematikai kérdések és érvelések is.

Köszönetnyilvánítás: A cikk írásához jelentős segítséget nyújtott Jonathan Block, Gunnar Carlsson, Frederick Chazal, Sasha Dranishnikov, Herbert Edlesbrunner, Benson Farb, Steve Ferry, Rob Ghrist, Alex Nabutovsky, Partha Niyogi, és Steve Smale; ezúton szeretném ezt nekik megköszönni.

Shmuel Weinberger
University of Chicago (USA)

A cikk eredetileg a Notices of the American Mathematical Society folyóirat What is... rovatában jelent meg 2011 januárjában. Ez a fordítás a szerző és az AMS engedélyével jelenik meg. A fordítást Stipsicz András készítette.

Shmuel Weinberger, WHAT IS...Persistent Homology? Notices Amer. Math. Soc. Vol. 58 Num. 1. (2011 January) 36-39 ©2011 American Mathematical Society. https://www.ams.org/notices/201101/rtx110100036p.pdf.

Irodalomjegyzék

: G. Carlsson, Topology and data, Bull. AMS 46 (2009), no. 2, 255–308.; H. Edelsbrunner és J. Harer, Persistent homology: A survey, Surveys on Discrete and Computational Geometry. Twenty Years Later, 257–282 (J. E. Goodman, J. Pach, and R. Pollack, eds.), Contemporary Mathematics 453, Amer. Math. Soc., Providence, Rhode Island, 2008.; J. Roe, What is a coarse space? Notices AMS 53 (2006), 668–669.

Lábjegyzetek

: ²Még akkor is, ha 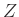$Z$ kompakt és 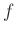$f$ folytonos, létezhetnek olyan szintek, amelyek homológiája végtelen dimenziós. De az a homológia, amely valamely pozitív hosszúságú intervallumon továbbél, már szüksegképp véges dimenziós – már ezért is érdemes ezeket az ún. perzisztens homológiacsoportokat közelebbről szemügyre venni. Amennyiben az 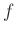$f$ függvény szép, a perzisztens homológia egy derivált, előretolt kéveként is felfogható.
: ³Egy végesen generált csoport esetén két elem távolsága azon generátorok minimális száma lesz, amelyekkel az egyik elemet szorozva végülis a másik elemet kapjuk. Bár ez a távolság függ a választott generátor-halmaztól, a kapott metrikus tér számos tulajdonsága független ettől a választástól, ahogy azt Roe [3] cikke elmagyarázza.