Sikerrel indult a Héttusa rovat versenye. Az első forduló hét feladatára összesen 69 helyes válasz érkezett.
Öröm látni, hogy van több általános iskolás és középiskolás résztvevőnk, vannak egyetemisták. Különleges öröm és megtisztelő, hogy országos, sőt nemzetközi hírű matematikusok is elküldték a megoldásaikat. A beküldők között látunk volt diákolimpikonokat, és látunk olimpikonokat felkészítő, ma már nyugdíjas tanárokat.
Három versenyző küldött hibátlan megoldást, és ketten adtak a hétből hat jó választ.
A feladatok nehézségi sorrendjét láthatjuk a beérkezett helyes válaszok száma alapján:
| A feladat sorszáma | 1. | 2. | 3. | 4. | 5. | 6. | 7. |
| A beérkezett helyes válaszok száma | 10 | 4 | 8 | 12 | 13 | 10 | 12 |
A következő táblázat mutatja, hogy a legeredményesebb beküldők mely feladatokra adtak helyes választ. (Vannak, akik a saját nevükkel szerepelnek, és vannak, akik másik nevet választottak maguknak.)
| A feladat sorszáma | 1. | 2. | 3. | 4. | 5. | 6. | 7. |
| Emil | x | x | x | x | x | x | x |
| Kovach M. László | x | x | x | x | x | x | x |
| orangestripes | x | x | x | x | x | x | x |
| Bubatov | x | x | x | x | x | x | |
| Jankó Zsuzsanna | x | x | x | x | x | x | |
| Beke Márton | x | x | x | x | x | ||
| Vaszary Krisztián | x | x | x | x | x | ||
| Belzebub | x | x | x | x | |||
| D & 2d | x | x | x | x | |||
| Megérek egy Petákot | x | x | x | x | |||
| Danka Emma | x | x | x | ||||
| Makay Géza | x | x | x |
Reméljük, hogy rovatunknak egyre több követője, megoldója lesz. Erre buzdítunk minden érdeklődőt! Szeretnénk olyan feladatokat kitűzni
- amelyek megoldására egy érdeklődő tizenévesnek is hasonló esélye van, mint egy nyugdíjas matematikatanárnak;
- amelyeken jó gondolkozni, érdekesek és több úton is megközelíthetjük a választ;
- amelyek újabb kérdéseket inspirálhatnak, elindulhatunk mélyebb és általánosabb vizsgálatok felé.
Az Érintő mostani számában olvashatjuk a 2. feladathoz kapcsolódó cikket Pálvölgyi Dömötörtől az Érmegráfokról, és készül egy másik cikk, amely az 1. feladatot járja körül..
Lelkesítő volt látni az érkező megoldásokat. A legeredményesebb beküldőknek a Typotex Kiadó és a Bolyai Társulat könyvjutalmakat ajánlott fel. A díjazottak ezeket a könyveket választották a Typotex kínálatából:
Válogatás Erdős Pál kedvenc feladataiból,
Az igazi Alan Turing,
2000 feladat az elemi matematika köréből;
a Bolyai Társulat és a Springer közös köteteiből:
Volume 26: Contact and Symplectic Topology, Szerkesztette: F. Bourgeois, V. Colin, A. Stipsicz,
Volume 27: New Trends in Intuitive Geometry, Szerkesztette: G. Ambrus, J. Bárány, K. Jr. Böröczky, G. Fejes-Tóth, J. Pach.
Mások pedig a KöMaL előfizetését választották.
A legjobb eredményt elért feladatbeküldők teljesítményét a továbbiakban is egy-egy könyvvel fogjuk elismerni.
A feladatok megoldása
1. Van-e olyan szám, amelynek pontosan tíz pozitív osztója van a 20-nál nem nagyobb számok között?
Megoldás. A válasz: Van ilyen szám.
Legyen 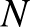 az 1 és 19 közötti páratlan számok szorzata. Az
az 1 és 19 közötti páratlan számok szorzata. Az 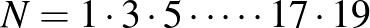 szám osztható az 1, 2, 3, 4, ..., 20 számok közötti páratlan számokkal, és nincs páros osztója.
szám osztható az 1, 2, 3, 4, ..., 20 számok közötti páratlan számokkal, és nincs páros osztója.
Megjegyzés. Más számok is teljesítik az elvárást.
60 esetén a megfelelő osztók: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20.
A 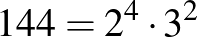 szám keresett osztói: 1, 2, 3, 4, 6, 8, 9, 12, 16, 18.
szám keresett osztói: 1, 2, 3, 4, 6, 8, 9, 12, 16, 18.
A 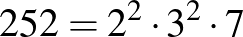 osztói közül a 20-nál nem nagyobbak: 1, 2, 3, 4, 6, 7, 9, 12, 14, 18.
osztói közül a 20-nál nem nagyobbak: 1, 2, 3, 4, 6, 7, 9, 12, 14, 18.
Az 1000-nél kisebb számok közül a 60, 144, 252, 336, 560, 792, 936 és a 990 számoknak van pontosan tíz pozitív osztója a 20-nál nem nagyobb számok között. Ha a számok bármelyikét olyan számmal szorozzuk, aminek minden prímosztója 20-nál nagyobb, akkor újabb megoldást kapunk, azaz olyan számot, amely teljesíti a feladat elvárását.
Többen félreértették a feladat szövegét, és erre a kérdésre válaszoltak: A 20-nál nem nagyobb számok között van-e olyan szám, amelynek pontosan 10 osztója van?
2. Egy asztallapra 11 egybevágó fehér korongot helyeztünk úgy, hogy a korongok között nincs átfedés. Igaz-e, hogy a korongokat mindig kiszínezhetjük úgy 3 színnel, hogy az egymással érintkező korongok különböző színűek?
Megoldás. A válasz: Hamis az állítás.
Két elrendezést mutatunk.
Az első esetben a korongok jól színezhetők 3 színnel.
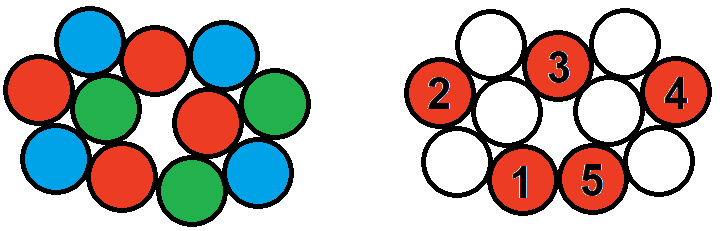
A második elrendezést már nem tudjuk 3 színnel jól színezni. Ha három színt használunk, és az 1-es korong piros, akkor a 2-es is piros színű lesz. Majd rendre pirossal kell színeznünk a 3, 4 és 5 számokkal jelölt korongokat. Mivel az 1-es és 5-ös érintkeznek, így szükséges egy negyedik szín is.
Tehát nincs minden esetben jó színezés 3 színnel.
Megjegyzés. Ez a feladat volt a legnehezebb, csak 4 helyes válasz érkezett, míg a többi feladatnál a helyes válaszok száma legalább 8.
Nehéz megtalálni egy olyan elrendezést, amikor szükség van 4 színre. Gondolhatjuk, hogy a 11 korong kiszínezhető 3 színnel, hiszen egy kör legfeljebb 6 másikkal érintkezhet, amelyek egymást is érinthetik, azokat felváltva színezem a maradék két színnel, és ugyanezt kiterjeszthetem az egész síkra is. Hihetőnek látszik, hogy elég 3 szín.
A megoldásból, a konstrukcióból látjuk, szükség lehet 4 színre. Tanulság, nem biztos, hogy a legszorosabb elhelyezés a legrosszabb.
A feladat hátteréről olvashatunk itt is: https://en.wikipedia.org/wiki/Penny_graph
Ha korongokat úgy helyezünk el a síkon, hogy nincs három olyan korong, melyek érintik egymást, akkor Erdős Pál szerint mindig elég 3 szín a színezéshez.
3. Legfeljebb hány pontot lehet megadni a kocka felületén, ha a pontok nem mind egy lapon fekszenek, és ezek egy szabályos sokszög csúcsai?
Megoldás. A válasz: 12.
A kocka egyik lapján legfeljebb két sokszög csúcs lehet, különben a teljes sokszög ezen a lapon feküdne. Ezért egy sokszögnek legfeljebb 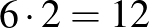 csúcsa lehet.
csúcsa lehet.
Van ilyen sokszög.
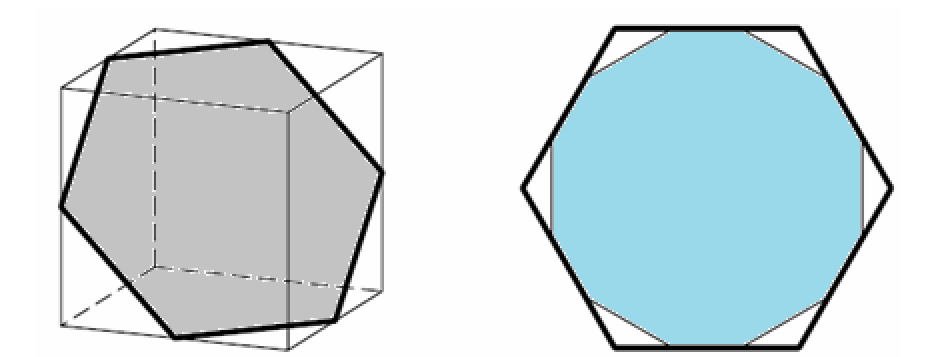
Vegyük az ábra szerinti élek felezőpontjait, amelyekről tudjuk, hogy szabályos hatszöget alkotnak. A hatszög oldalain felvehetünk 2-2 pontot (a hatszög oldalai a kocka oldallapjain nyugszanak) úgy, hogy az így adódó 12-szög szögei egyenlők, és az oldalai is egyenlők, tehát ez szabályos 12-szög.
Megjegyzés. Ez a feladat a feladatok nehézségi sorrendjében a második.
Az egyik tipikus rossz válasz a 8. A kockának van olyan síkmetszete, amely négyzet, és azon kijelölhetjük egy szabályos nyolcszög csúcsait.
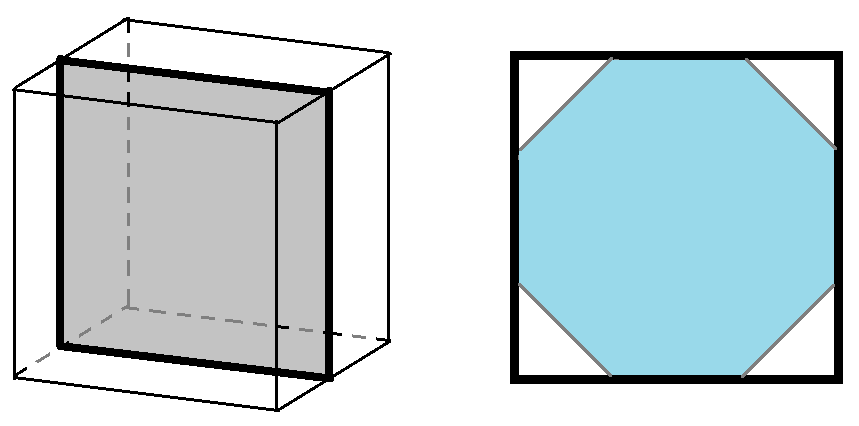
Érkeztek tippek a 6-ra is, hiszen a kockának van szabályos hatszögmetszete. (Onnan lehet továbblépni, és eljutunk a 12-höz.)
A KöMaL 1974. novemberi számában Kolmogorov: A matematikusi hivatásról c. cikkében ezt olvashatjuk:
Például már ragyogó matematikusnak kell lenni ahhoz, hogy csukott szemmel, ábra nélkül, világosan el tudjuk képzelni magunknak egy kocka felületének azt a síkmetszetét, melynél a metsző sík merőleges a kocka egyik testátlójára és átmegy annak középpontján.
Képzeljük el! Mi lesz a síkmetszet?
4. Van-e négy olyan racionális szám, melyek egyike sem egész, de bármely két szám szorzata egész szám?
Megoldás. A válasz: Vannak ilyen számok.
Veszek négy prímet, és képezem három szorzatát osztva a negyedikkel.
Például: 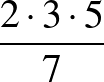 ,
, 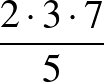 ,
, 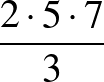 és
és 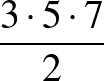 .
.
5. Egy kör alakú nyakláncon 15 kék és néhány piros gyöngyszem van. A lánc bármely olyan szakaszán, ahol van 6 kék gyöngyszem, ott legalább 3 piros gyöngyszemet is találunk. Legkevesebb hány piros gyöngyszem van ezen a láncon?
Megoldás. A válasz: 9.
A láncon 8 szomszédos gyöngyszem között legfeljebb 5 kék (így legalább 3 piros) gyöngyszem van, hiszen ha lenne legalább 6 kék szem, akkor már nem lehet 3 piros, amit a feltétel elvár.
Nézzünk 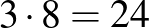 egymás után sorakozó gyöngyszemet. Közöttük legfeljebb
egymás után sorakozó gyöngyszemet. Közöttük legfeljebb 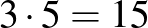 kék, és legalább
kék, és legalább 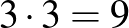 piros gyöngyszem van.
piros gyöngyszem van.
Ha a láncon 15 kék szem van, akkor van legalább 9 piros gyöngyszem is.
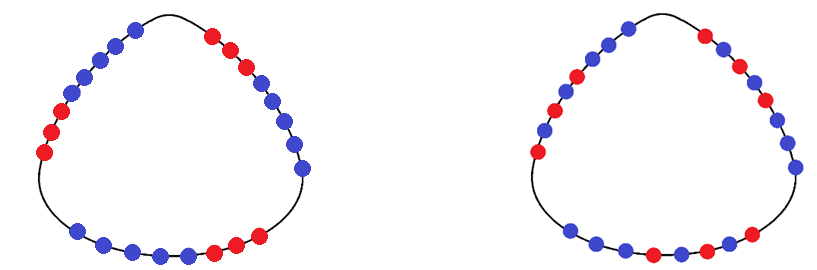
Van olyan nyaklánc 15 kék szemmel, amelyen 9 piros gyöngyszem van, és teljesül az elvárt feltétel. Két ilyen láncot látunk az ábrán.
Megjegyzés. Az egyik beküldő így indokolt:
A válasz 9. Erre pl. jó megoldás az 5 kék 3 piros váltakozva. Ennyi viszont szükséges is. Ugyanis tekintsük a 15 kéket 3 diszjunkt 5-ös csoportban, ahol a két szélső is kék. Ekkor tekintsük, hogy hány piros van az 5-ös csoportokon belül. Ha mindegyik legalább 3 pirosat tartalmaz, akkor kész. Ha kevesebbet, akkor viszont a csoport szélső kékje mellett mindkét oldalon pirosnak kell következnie. Ha belül 2 piros volt, akkor 1-nek, ha belül 1 piros volt, akkor kettőnek, ha belül 0, akkor 3-nak. Számoljuk a pirosakat az 5-ös csoporton belül és tőle az óramutató járásával egyező irányban. Ez az összeg a feladat feltétele miatt mindig legalább 3. Tehát kell 3-szor 3 piros.
6. Az újoncok felálltak egy sorban az őrmesterrel szemben. A „balra át” parancsra néhányan balra, a többiek jobbra fordultak. Kiderült, hogy kétszer több katona nézi a szomszéd hátát, mint az arcát. Ezután a „hátra arc” parancsra mindenki az ellenkező irányba fordult, és most háromszor több katona nézi a szomszéd hátát, mint az arcát. Hány katona áll a sorban?
Megoldás. A válasz: 18.
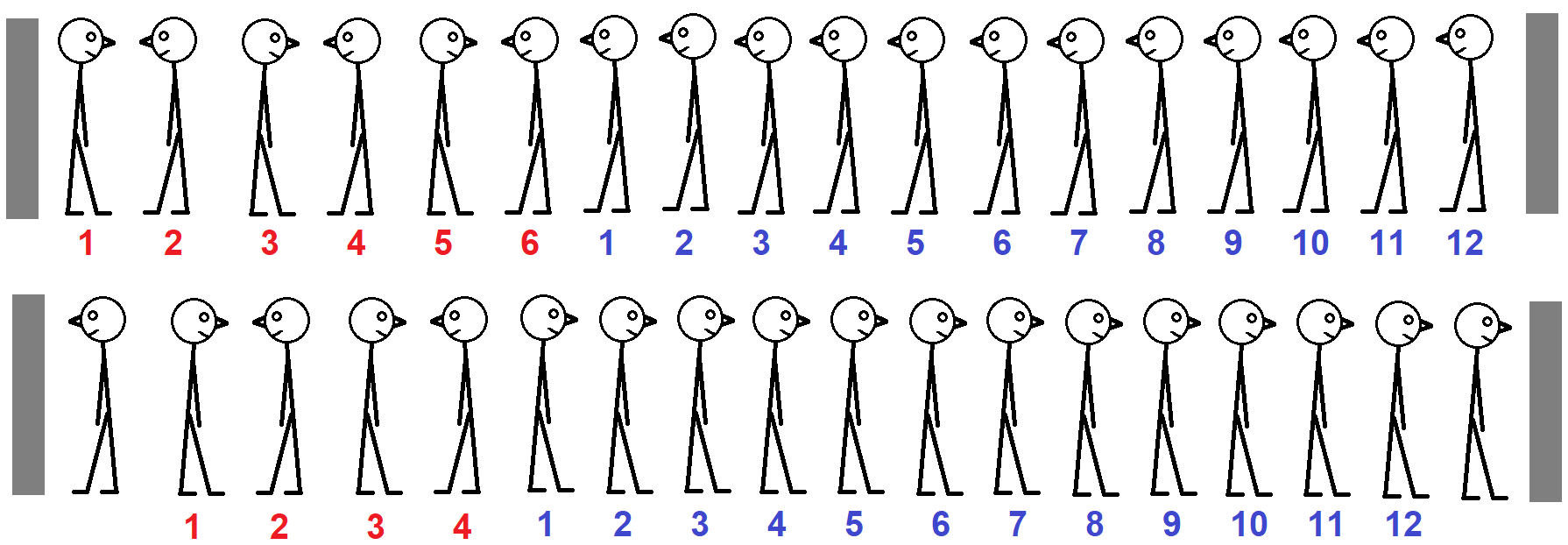
Tegyük fel, hogy a katonák két oszlop között sorakoznak. Az első parancs után minden újonc a szomszédja hátát vagy az arcát nézi, kivéve a szélen lévő két katonát, akik nézhetik az oszlopokat is.
Vegyük észre, hogy a „hátra arc” parancs után is ugyanannyian nézik a szomszéd hátát, mint korábban, ez nem változik. Válasszunk két szomszédos katonát, ha egyikük a másik hátát nézi, akkor megfordulás után ez a szomszéd nézi az előbbi katona hátát. Akinek eddig a hátát nézték, fordulás után ő fogja a másik hátát nézni. A szélen álló katonák megfordulása sem változtat a szomszéd hátát nézők számán. Csak a szomszéd arcát nézők száma változhat.
Az első parancs után 2-szer annyian nézik a szomszéd hátát, mint a szomszéd arcát. A második parancs után ez az arány 3-szorosra nő.
Ha az első parancs után azok száma, akik a szomszéd arcát látják 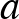 , a második parancs után pedig
, a második parancs után pedig 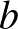 , akkor a szomszéd hátát nézők száma
, akkor a szomszéd hátát nézők száma 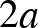 , illetve
, illetve 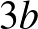 , és mint tudjuk, ez mindkét esetben ugyanannyi:
, és mint tudjuk, ez mindkét esetben ugyanannyi: 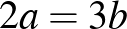 . Tehát a szomszéd arcát nézők száma csökken a második parancs után.
. Tehát a szomszéd arcát nézők száma csökken a második parancs után.
A csökkenést a szélen álló katonák megfordulása teszi lehetővé. Ha körben állnának az őrmester körül, akkor ezek a számok nem változnak, mert ekkor minden katona az egyik szomszédjának az arcát vagy a hátát nézi, tehát ennek a kétféle számnak az összege állandó (azonos a katonák számával). Mivel a másik hátát nézők száma változatlan, így a szomszéd arcát nézők száma is állandó.
A katonák azonban most sorban állnak. A két szélső katonát kell figyelnünk. Ha fordulás előtt a két szélső katona közül az egyik az oszlopot nézi, a másik a szomszédját, akkor a fordulás után is ilyen helyzet lesz, ekkor nincs változás a szomszédokat nézők számában. Emiatt nem változik a szomszéd arcát nézők száma. Ha mindkét szélső katona az oszlopot nézte, akkor a fordulás után 2-vel növekedne a szomszédokat nézők száma, azaz a szomszéd arcát nézők száma (hiszen a hátát nézők száma változatlan), ami ellentmond a feladat feltételének, ami a szomszéd arcát nézők számának csökkenését jelenti.
Ha a két szélső katona a fordulás előtt a szomszédját nézi, akkor a fordulás után az oszlopokra néznek. Most csökken a szomszédokat nézők száma 2-vel, így 2-vel csökken a szomszéd arcát nézők száma.
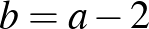 . Mivel
. Mivel 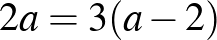 , innen
, innen 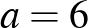 . Ha tehát az első parancs után senki nem néz az oszlopokra, akkor 6 nézi a szomszédja arcát, és
. Ha tehát az első parancs után senki nem néz az oszlopokra, akkor 6 nézi a szomszédja arcát, és 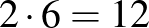 a szomszédja hátát. Összesen
a szomszédja hátát. Összesen 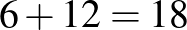 újonc sorakozik az őrmester előtt.
újonc sorakozik az őrmester előtt.
Megjegyzés. Az egyik beküldő így indokolt:
18 katona. Jelölje 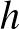 a hátat,
a hátat, 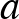 az arcot látó katonák számát. A szélen kifelé nézők nem számítanak. Megforduláskor
az arcot látó katonák számát. A szélen kifelé nézők nem számítanak. Megforduláskor 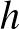 változatlan. Az
változatlan. Az 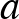 értéke pedig 2-vel nő.
értéke pedig 2-vel nő.
Ezért 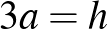 és
és 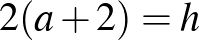 . Ebből
. Ebből 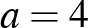 és
és 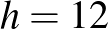 .
.
7. A varázslótanoncok iskolájában 7 tanítvány ül egy asztal körül, jövendölésből vizsgáznak. Mindenki megjósolja, hogy önmagát és a két szomszédját kivéve a többi 4 tanonc közül kinek lesz majd sikeres a vizsgája. Egy vizsga akkor sikeres, ha a vizsgázó tanoncnak mind a 4 jóslata beválik. A tanoncok nem bíznak társaik képességeiben, mindenki azt jósolja, hogy sikertelen lesz a többiek vizsgája. Hányan mehettek át a vizsgán?
Megoldás. A válasz: Pontosan 2 tanonc ment át.
Van olyan vizsgázó, aki átment, hiszen ha minden tanonc kudarcot vall, akkor bármely 4 egymás melletti tanoncról nyilatkozó vizsgázónak igaza lenne, így sikeres lenne a vizsgája, ami ellentmondásos.
Tegyük fel, hogy Baltazár átmegy a vizsgán.
Ezért az a 4 vizsgázó, akikről nyilatkozik, sikertelen vizsgát tesz. Ez a 4 vizsgázó valóban sikertelen ebben a helyzetben. Ugyanis nézzük a 4 vizsgázó egyikét, Nostradamust. Ő azt jövendöli, hogy a vele nem szomszédos 4 vizsgázónak sikertelen lesz a vizsgája, ám közöttük van Baltazár, aki átment a vizsgán. Így Nostradamus jóslata nem vált be, valóban sikertelen a vizsgája.
Tehát a Baltazárral nem szomszédos 4 tanonc egyike sem sikeres.
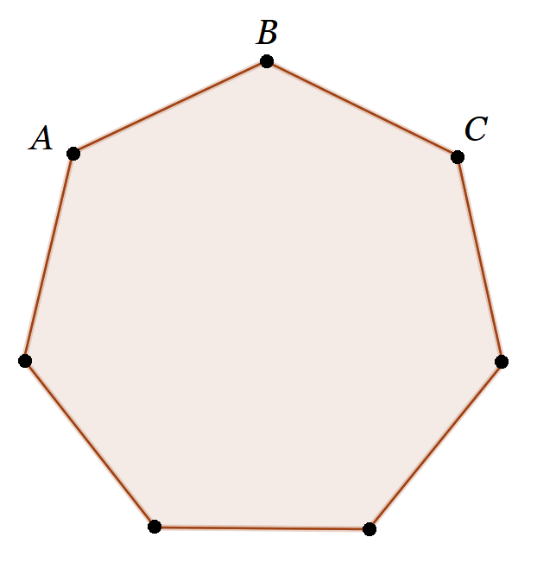
Van még két vizsgázó, Baltazár szomszédai, ők Amina és Cassandra. Vajon sikerült-e a vizsgájuk?
Ha Amina jóslata beválik, akkor a vele nem szomszédos 4 tanonc tévesen jósol, köztük Cassandra is. És valóban, Cassandra jóslata téves, mert Amináról is azt jövendölte, hogy nem válik be a jóslata.
Ha Amina jóslata téves, az csak úgy lehet, ha Cassandra jól látja a jövőt, és valóban, Cassandra jóslatai teljesülnek.
Tehát Baltazár egyik szomszédja teljesíti a vizsga követelményét, a másik szomszéd nem.
Azt kaptuk, hogy a 7 tanítványból valamely két szomszédos tanonc sikeresen vizsgázik, a többiek hibásan jósolnak.
Megjegyzés. Két indoklás a beküldőktől:
Ketten. Legyenek a tanoncok körben 1, 2, 3, 4, 5, 6, 7. Lehetetlen, hogy mindenki megbukott, mert 4 egymás melletti bukottal szembeni tanonc minden jóslata talált. Ha van legalább egy sikeres vizsgázó, legyen ez a 2-es. Ekkor 4, 5, 6, 7 megbukott. Ha 3 megbukott, akkor 1 átment. Vagy fordítva.
Két egymás mellett ülő varázsló ment át, mert ők egymásnak nem jósolnak, tehát igaz hogy 4 nem megy át. A többi 5 varázsló is azt jósolja hogy senki nem megy át, de nekik benne van a két sikeres vizsgázó tehát nem válik be a jóslat.
Az egyik beküldőtől ez a válasz érkezett: 2, de ez egy nagyon igazságtalan vizsga.
Róka Sándor











