Fejér Lipót tanítványa voltam

Részletek Ottlik Géza írásaiból

Félbeszakadt beszélgetés Réz Pállal

Ez az interjúnak szánt beszélgetés elakadt, nem lett belőle semmi annak idején. Az én hibámból. Túl sokat beszéltem túl kevés dologról, s ráadásul fontos magánügyeimről, amelyek túlságosan személyesek ahhoz, hogy a rádión keresztül a hallgatókat érdekelhessék. A könyv olvasójával sokkal személyesebb, valódibb kapcsolatban van az író. Ez nem „tömegkommunikációs eszköz”. Aki unja, az leteszi vagy átlapozza. Aki kíváncsi rá, végigolvassa – és talán a sok személyes fontoskodást sem bánja benne.

…

– Mikor jelent meg nyomtatásban először írásod?

– Nemsokára. 1931-ben. Még nem voltam tizenkilenc éves. Egy előkelő irodalmi folyóirat közölte két kis novellafélémet tavasszal, de mire nyáron a harmadik is megjelent, már nem lehetett nem észrevennem, hogy szégyenlétesen rosszak mind. Nagy csapás volt ez nekem. Sokk vagy trauma, ahogy tudálékosan mondhatnám, de tényleg seb, nem múló sérülés. Vereség. Mondom, versenyző vagyok – vereséggel kezdtem a pályát, de a világrekorderek is vereséggel kezdik –, a vereségek fontos dolgok, a futók tudják jól. Belemerültem tehát a matematikába és a filozófiába. Nekifogtam egy egzakt filozófiai nyelv megszerkesztésének – mert azzal is baj volt, elakadtam a híres nagy bölcseleti művekkel, amelyek mind a köznapi nyelv ambivalens, rosszul definiált szavait használták. Álgörög kifejezéseket eszkábáltam; aztán jött a második vereségem: szaporodtak a céduláim, elárasztottak a szobámban; gyártottam őket rendületlenül. Mielőtt belefulladtam volna képtelen vállalkozásomba és a céduláimba, szemétbe dobtam az egészet, és kimentem az új tavaszba, le az édes Budapestre, táncolni rumbát a szép, undok lányokkal és bridzsezni a csúnya kedves fiúkkal.

– Közben egyetemre is jártál?

– Igen, Fejér Lipót tanítványa voltam. Magyar–francia–matematika szakra akartam beiratkozni, ki is töltöttem a nagy barna íveket, de a tanárképzőben figyelmeztettek, hogy ez együtt nem megy, húzzam ki a matematikát. Vitatkozni próbáltam, még csak nem is válaszoltak, persze; mire dühömben kihúztam a magyart és franciát. Önfejű, pökhendi zöld kölyök indulatos meggondolatlanságában ritkán csinált még ilyen bölcs dolgot. Matematikából abszolváltam négy év múlva, sőt doktorálni készültem hat év múlva.

– Láttad-e hasznát matematikai és fizikai tanulmányaidnak mint író?

– Nem tudom. G. M. Hardy szerint a matematikának az a létjogosultsága, hogy nincs semmi haszna. Talán inkább úgy áll a helyzet, hogy ez teljesen irreleváns szempont: a matematika messze fölötte áll minden evilági és túlvilági hasznossági kritériumnak, akárcsak a művészet. Ettől még véletlenül hasznuk is lehet, mind a kettőnek: szerintem csakugyan, véletlenül mind a ketten az emberiség létét, életben maradását biztosítják. De persze, ha nem tennék, vagy az ellenkezőjét tennék, akkor is azok lennének, amik, s éppoly elpusztíthatatlanok. Talán láttam hasznát annak a lélektani „algoritmusnak”, amit a matematikustól lestem el. Például, ahogy már említettem, hogy az író hallgasson, ha nincsen semmi mondanivalója. Ez nem olyan egyszerű követelmény, mint ahogy hangzik. Végtére is a költőt mindenekfelett közlésvágy mozgatja. Hisz magában, mondanivalója fontosságában. Ezt a hitét nem engedheti megingatni. Ezért aztán be nem áll a szája. Mindenhez hozzászól, kiteregeti, elemzi, közli a lelkét, aggódik a haza sorsáért, megváltja az emberiséget. Bölcseleti rendszert alapít, elutasítja a Nobel-díjat, leírja apróra a gyerekkorát. Mindezt szakszerűen csinálja, jól, hozzáértéssel, s amit ír, az mind helyes, hasznos és igaz. Mit lehet ebben kifogásolni? Csupán azt, hogy ez olyasféle eljárás, mint ha valaki, aki megtanult szorozni-osztani, harminc éven át különböző szorzásokat és osztásokat végezne el, és közölné a – helyes, igaz – eredményeket könyv alakban. Hát még ha hatványozni és gyököt vonni is megtanult, vagy netán differenciálni és integrálni: micsoda orgiákat rendezne az öncélú műveletvégzésekből! A matematikus, ha elkészített egy szerszámot, sohasem használja többé, eldobja: amit megtart, az a szerszám elkészítési módja, a módszer, amivel célt ért – az „algoritmus”. Sohasem számít ki eredményeket: a matematika épületén dolgozik. Fejér Lipót olyan nagy volt, hogy nemcsak szorozni-osztani, de differenciálni-integrálni sem tudott. (Zárójelben: ezt úgy értsük, hogy – ha nem lett volna már felfedezve – fel tudta volna fedezni az infinitezimális-számítást, de használni nem tudta, nem volt képes a figyelmét ilyen alacsonyra lecsavarni.) Ha a táblán egy ilyen sorhoz ért, kissé gyötrött hangon hátraszólt rendszerint: „Diktálják, kolléga urak!” Néha pedig kizökkent: az Egyetemi Nyomda zajos teherautója kanyarodott az ablak alá, Lipi idegesen elhallgatott, becsukta az ablakot, visszajött, tanácstalanul bandzsított ránk, majd a táblára, elolvasta, amit addig felírt rá, s lassacskán rájött, hogy hol is van és miről ad elő. „Á, á!” – mondta felderülve. Nyilvánvaló volt, hogy miközben előad, egészen másutt jár az esze. Nem is az esze, hanem egész valója, valamerre, ismeretlen, hallatlan, számunkra elérhetetlen távoli tájakon jár. Ezt a bűvészmutatványát úgy csinálta, hogy a nyolcad- vagy tizenhatod-figyelemmel előadott igen nehéz tárgyát még az is erőfeszítés nélkül rögtön megértette, aki esetleg szintén csak félig figyelt a szavaira. Én olyat is megértettem nemegyszer az előadásából – vagy a testi jelenlétéből? –, amit nem mondott, nem mondhatott. De ez már szakmabeli magyarázatot kívánna. Kívülállónak nem lehet elmondani, hogy milyen volt Fejér Lipót. Óriás volt. Földöntúli vigasztalás a puszta lénye. Aki nem ismerte, az valamit nem tud a világról, és sohasem is fogja megtudni.

– Kívülálló is felfogott valamit belőle mégis, ahogy mesélted egyszer, amikor beültek az órájára zöldsapkás jogászok, tüntetni ellene, és végül meg sem moccantak…

– Már negyedévesek voltunk, amikor egyszer felrohantak értünk a lányok, kolleginák, hogy az ötös teremben idegenek vannak, nyilván meg akarják zavarni Lipi előadását. Mire a barátommal lóhalálában leértünk a laborból, Fejér Lipót már ott volt a katedrán. Elkéstünk. Most már nem lehetett kidobni az idegen hallgatókat, csak leültünk a hátsó sorban, és hátulról figyeltük minden mozdulatukat. Kár volt lerohannunk. Az elszánt „tüntetők” két óra hosszat mozdulatlanul, dermedten, hipnotizálva a delejes varázstól, ami megtöltötte a termet, s amit ez a finomszálú szőkeőszes hajú, nagykeretes szemüvegű, félrebillentett fejjel kancsin a levegőbe bámuló férfi árasztott, megbabonázva csak ültek némán, tátott szájjal, véges-végig. De hát ez csak állatszelídítés volt Fourier- és Laplace-sorokkal. Koromzay Dénes barátom, a világhírű Magyar Vonósnégyes brácsása, mesélte nekem vagy harminc évvel később, hogy egy előkelő amerikai fogadáson valahogyan egy nagynevű ottani matematikaprofesszor mellé került, aki láthatólag jól értett a zenéhez. Dénes, csak hogy mondjon valamit, megjegyezte, hogy az ő barátjának is, mármint nekem, volt egy zeneértő matematikaprofesszora, akit ők nagyra tartottak, Fejér Lipótnak hívták, de hát nem valószínű, hogy valaha is hallotta volna a nevét itt Amerikában. Mire az idős professzor felhördült, elvörösödött, hebegni kezdett, hátrált: „Hogy – hogy – hogy – hogy hallottam-e a nevét? Ember! Életem legnagyobb élménye, hogy egyszer egy kongresszuson ötlépésnyire álltam Fejér Lipóttól! Ott állhattam egészen közel hozzá! Ez évtizedekre erőt adott nekem!”

– Úgy tudom, Fejér Lipót Adyval is barátságban volt. Azt mondod, nagy hatással volt rád Ady Endre, de én ennek semmi nyomát nem látom az Iskola a határon-ban. Egyébként dolgozol a folytatásán? Vagy mást csinálsz? Vagy semmit?

– Ezt is csak a matematikus érti meg és a művész, hogy az ember mást csinál, másról beszél, vagy semmit sem csinál, csak van, borotválkozik, vagy megy át a Kálvin téren este nyolckor, és megvilágosodik előtte egy tiszta kép, forma, megoldása mindannak, ami hetek, hónapok, évek óta megoldatlan. S ami mélyen elmerülve munkálódott, készült valahol az emberben. Ehhez kell az írónak is a földtani türelem. Nem csupán növényi, ahogy Valéry írja a pálmafáról:

„Patience, patience,
Patience dans l'azur!

– Chaque atome de silence
Est la chance d'un fruit mûr!”

– Szóval a hallgatásod minden atomjában egy új regény esélye érlelődik…?

– Mondom, hogy geológiai türelem kell hozzá, nem elég a növényi. No de, hagyjuk abba, már túl hosszúra nyúlt úgyis.

– Nem, nem, beszéljünk a regényről.

– Sok lesz, fejezzük be inkább.

– Ki megy át a Kálvin téren este nyolckor, Bébé vagy Medve Gábor? Ez már a regényben lesz, fogadjunk…

– Nyertél. Jó füled van. Hát folytassuk. Egyelőre csak én mentem át a Baross utca felé, 1930-ban. Mint elsőéves, októberben beneveztem egy matematikai versenyre az egyetemen. Első feladatnak szándékosan egy könnyűt adtak. Ezen rögtön elvéreztem. Végül alig maradt időm a nehezebbekre. Olyan egyszerű volt, hogy te is megértheted: nézd, leírom. Számelméleti segédeszközök nélkül kellett bebizonyítani, hogy, ha 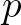$p$ kettőnél nagyobb prímszám, akkor a

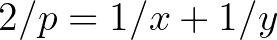
$\displaystyle 2/p=1/x+1/y$

egyenletnek mindig van egy, és csakis egy, pozitív egész számú megoldása (a triviálistól, 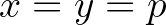$x=y=p$ , eltekintve). Egészen rosszul vágtam neki. A számelméletről még fogalmam sem volt, csak annyi, hogy akkor még utáltam. Tudod, csak egész számokkal foglalkozik, oszthatósággal, a gyönyörű, karteziánus folytonosság helyett. Milyen oldalról lehet ennek nekimenni? Órákat pocsékoltam rá. Dühömben végül felrajzoltam a görbéjét, aminek semmi köze a feladathoz:

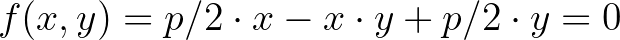
$\displaystyle f(x,y)=p/2\cdot x-x\cdot y+p/2\cdot y=0$

Ezen az alakján talán te is rögtön látod, hogy ez egy elforgatott hiperbola, a koordinátatengelyekkel párhuzamos aszimptotákkal. De azt az atyaisten se tudná megmondani, hogy van-e olyan pontja, melynek a koordinátái kifejezhetők pozitív egész számokban – és nem is kíváncsi rá! Persze a diophantoszi egyenleteket nem szabad emberszámba venni…

– Hagyjuk hát Diophantoszt, és gyerünk át a Kálvin térre inkább…

– Elfeledkeztem az egészről, pedig ez megint egy fontos vereség volt, de a filozófiai szótár-készítés mellett prózát, novellát vagy prózaversfélét próbáltam írni, jártunk a Fedett Uszodába a kolleginákkal, megjött a november, megjött a december, jártam a nővéremmel, akit nagyon szerettem, s aki zenekritikus volt, koncertekre, a Zeneakadémiára, s ami a fő, utána sörözőkbe, kávéházakba, az ő kollégáival, Lányi Viktorral, Tóth Aladárral, jártam a Mester utcába a szép Adi kedvéért, amíg a még szebb Sári meg nem jött Léváról, s karácsony hetében megint egyszer a nővéremékhez mentem, s ahogy átvágok a Kálvin téren, töprengve, hogy mutassam-e meg neki legújabb próza-művecskémet, abban a szempillantásban megjelenik a fejemben a nyavalyás kis diophantoszi egyenlet pofonegyszerű megoldása. Nézd, három sor az egész. Szorozd meg 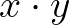$x\cdot y$ -nal:

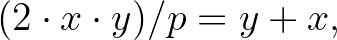
$\displaystyle (2\cdot x\cdot y)/p=y+x,$

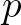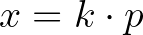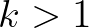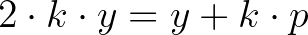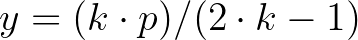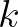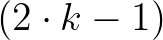ahol a jobb oldal egész szám, s a bal oldal csak akkor lehet egész szám, ha valamelyik ismeretlen osztható $p$ -vel. Mondjuk: $x=k\cdot p$ ( $k>1$ és egész szám). Behelyettesítve a fentibe: $2\cdot k\cdot y=y+k\cdot p$ . Innen: $y=(k\cdot p)/(2\cdot k-1)$ . Minthogy $k$ és $(2\cdot k-1)$ relatív prímek (nincs közös osztójuk), 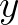$y$ csak akkor lehet egész szám, ha a 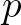$p$ (prímszám!) osztható 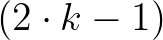$(2\cdot k-1)$ -gyel: vagyis nyilván csakis akkor, ha 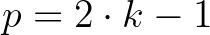$p=2\cdot k-1$ . Azaz, ha: 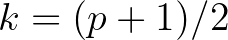$k=(p+1)/2$ . Tehát

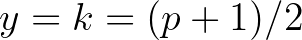$\displaystyle y=k=(p+1)/2$ és $\displaystyle \quad x=p\cdot[(p+1)/2].$

Kész. Érted?

– Véletlenül még értem is. De talán most már mégis hagyjuk abba…

– És, amint láthatod, két megoldása van mindig, nem egy és csakis egy…

És, amint láthattam, ha a matematikában is ki vagyok szolgáltatva az akaratomtól független ismeretlen beavatkozás súgásának, segítségének, helyettem való munkálkodásának, hát maradhatok nyugodtan az irodalomnál - - - - - -

[Egyetem, BH]

Sok minden félbeszakad, elakad, abbamarad. Felhagytam végül az újságírással is, miután még egy nagy reggeli lapnál megpróbálkoztam. Úgy látszik, a világ ilyen szakadásos. Ezeket a szakadásokat a lelkünk nem veszi szívesen, nem is mindig tudja követni, elfogadni, magáévá tenni: folytonosságot kíván. A folytonosság azonban előfeltételezi a végtelen fogalmát, tényleges létezését – hogy például a párhuzamos egyenesek ott találkozhassanak, vagy hogy egy görbének két, egymáshoz bármilyen közel fekvő pontja között mindig legyen még sok más pontja is. A természet világában, úgy látszik, nincsen folytonosság és végtelen. Emlékszem, a szó szoros értelmében fájdalmasan érintett Planck hatáskvantum-elmélete. De sok nagy matematikus sem szerette, ha csúfot űztek a folytonosságból. „Borzalommal és iszonyodva fordulok el ezektől a függvényektől, amelyeknek nincsen deriváltjuk”, írta az egyik. 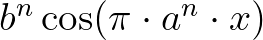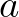Weierstrass már 1861-ben megmutatta, hogy az a sor, melynek általános tagja: $b^n\cos(\pi\cdot a^n\cdot x)$ (ahol $a$ páratlan egész szám, 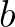$b$ valódi tört 0 és 1 között) azzal a feltétellel, hogy: 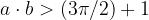$a\cdot b>(3\pi/2)+1$ az 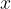-nek egy folytonos függvényét definiálja, melynek a változó semelyik értékénél nincs deriváltja. Ettől nem kisebb ember, mint Hermite fordult el „félelemmel és irtózattal”.

Mindezzel talán ellentétben, beleszerettem váratlanul a csoportelméletbe, vagyis a félelmetesen absztrakt Van der Waerden Modern Algebrá-jába (de inkább csak a véges nem-kommutatív csoportokba). Talán a harmadik fejezetnél evvel is elakadtam. Már egy árva szót sem értettem belőle. De nem volt baj, jártunk át a Múzeum körútról a Műegyetemre is, számelméletet hallgatni, és útközben a Vámház körúton nemrég megnyílt automatabüfébe mindig betértünk; ez újdonság volt akkor Budapesten, elég drága, húsz fillért kellett bedobni, de csodálatos majonézes, velős, gombás, ringlis szendvicseket eresztett alá az üvegtornyos masina – amit választottál –, és a pohár sört is annyiért csurgatta ki, egy hatosért; a Van der Waerdent pedig sok-sok év múlva megint kivettem az Egyetemi Könyvtárból, százesztendőnyi fiatalság és hétévi háború múltával, épp nagyon jól jött a hűvös elvontsága, tömör eleganciája. A Múzeum körút földszintjén, az ötös teremhez kapcsolódva, volt egy Matematikai Szemináriumnak nevezett, tágas, klubszerű helyiségünk, saját kulcsunk hozzá, fiókunk, fehér köpenyünk, holmink benne, meg egy már kialakult szűkebb klikkünk a kollégákból: a Műegyetemre rendszerint velük, öt-hat fiúval és kedves, okos lánnyal, gyalog sétáltunk át, mert egy teljes üres óránk volt közben; s attól félek, elég zajosan, harsogva, meg-megállva. A sok nevetéstől kifulladva, éppen kellett útközben a vadonatúj automatabüfé.

Az egyetem miatt nem kellett volna feladnom az újságírást; elég volt déltájt bemennem, csak a kémiaprofesszorunk olvasott néha katalógust; ámbár ez veszélyes volt, mert a jámbornak látszó, öreg, unalmas fajankó, nevezzük Kovácsovszkynak, képes volt két abszenciáért elveszíttetni velünk a félévet, a gyenge és gyáva emberre jellemző durva kíméletlenségével – amit senki más professzor meg nem tett volna. De itt is megvédtük egymást, telefonáltak értem, ha a jóindulatú tanársegédje tüntetően kirakta az óra előtt a nagy katalógust, vagy jelentkezett valaki helyettem egyszerűen (és vakmerően).

…

Ottlik Géza