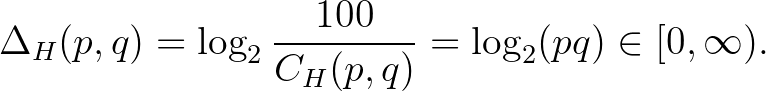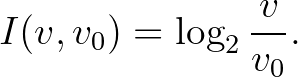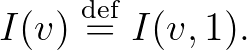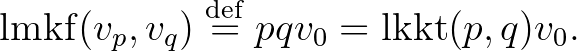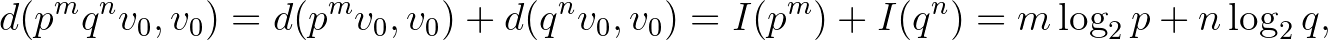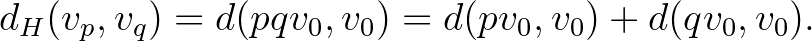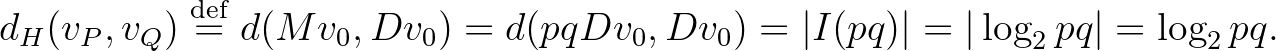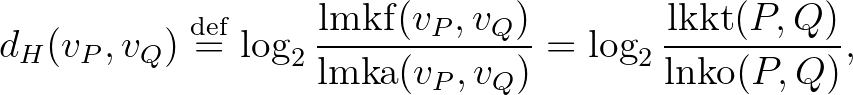Bevezetés
Mitől találunk szépnek valamit? Az ember ősidők óta keresi a választ erre a kérdésre. Talán mindnyájan érezzük, hogy csakúgy, mint egy andalító dallam élvezetéhez, a szépség megéléséhez is elengedhetetlen a harmónia.
A cikkben a zenei szépségnek csak apró szeletét fogjuk vizsgálni, amelyet a következő helyzet nagyszerűen szemléltet. Ha csukott szemmel leütünk egyszerre két billentyűt a zongorán, elképzelhető, hogy a két hang együttese kellemes érzéssel tölt el minket, azaz konszonáns, ám az is, hogy feszítő, fülsértő lesz a hatás, azaz disszonáns. A cikk elején fény derül rá, fizikailag milyen eszközzel lehet mérni ezt az érzetet, illetve bevezetünk egy mérőszámot is a matematikai leíráshoz. Itt természetesen a hangoknak megfelelő frekvenciákkal számolunk, hiszen a hangok és a frekvenciák között bijekció áll fenn. Bevezetünk egy zenészek által ugyan nem használt, ám a matematikai értelemben vett távolság fogalmának eleget tevő mennyiséget. Ennek segítségével kapcsolatba lehet hozni ezt a bizonyos szépségérzetet hangok távolságával. Ezt egy gráfstruktúrán is szemléltetni fogjuk. Eleinte relatív prím frekvenciák között definiálunk távolságot, de később ezt általánosítani fogjuk tetszőleges egész frekvenciákra is.
A zenei szakkifejezések definícióit a cikk végén találhatják.
Konszonancia- és disszonanciamérés
Mindenek előtt el kell különítenünk egy zenei hangban az alaphangot a felhangoktól. Az így megtisztított hangoknak már tudjuk nézni az interferálását, amellyel összefüggésbe hozható a konszonancia- és disszonanciaérzet. Ebben a fejezetben a megtisztítás metódusát mutatjuk be, majd az összefüggés leírására mérőszámokat vezetünk be.
Helmholtz1 a rezonátor nevű eszközt használta, hogy kiszűrje a felhangokat egy összetett hangból, és számszerűsítse a disszonancia mértékét a lebegésre való tekintettel. Az 1. ábrán látható műszerek paramétereinek (üreg térfogata, nyak keresztmetszete, nyak hossza és ennek megváltoztatása) függvényében lehet mérni és számolni.

1. ábra: Helmholtz rezonátorai. Forrás: https://physics.case.edu/about/history/antique-physics-instruments/helmholtz-resonator-2/
Két interferáló hullám frekvenciáját folyamatosan változtatva Helmholtz rájött, hogy azok a frekvenciák, amelyek megtartanak egy racionális arányt, növelik a konszonanciaérzetet. Egy 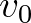 alaphang
alaphang 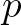 -edik és
-edik és 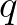 -adik felhangját tekintve a konszonancia mértéke nagyjából számszerűsíthető úgy, mint a
-adik felhangját tekintve a konszonancia mértéke nagyjából számszerűsíthető úgy, mint a 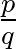 hányados, ahol
hányados, ahol 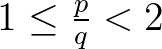 . Tehát minél kisebb az arány, annál kisebb a konszonancia (leszámítva az 1 értéket).
. Tehát minél kisebb az arány, annál kisebb a konszonancia (leszámítva az 1 értéket).
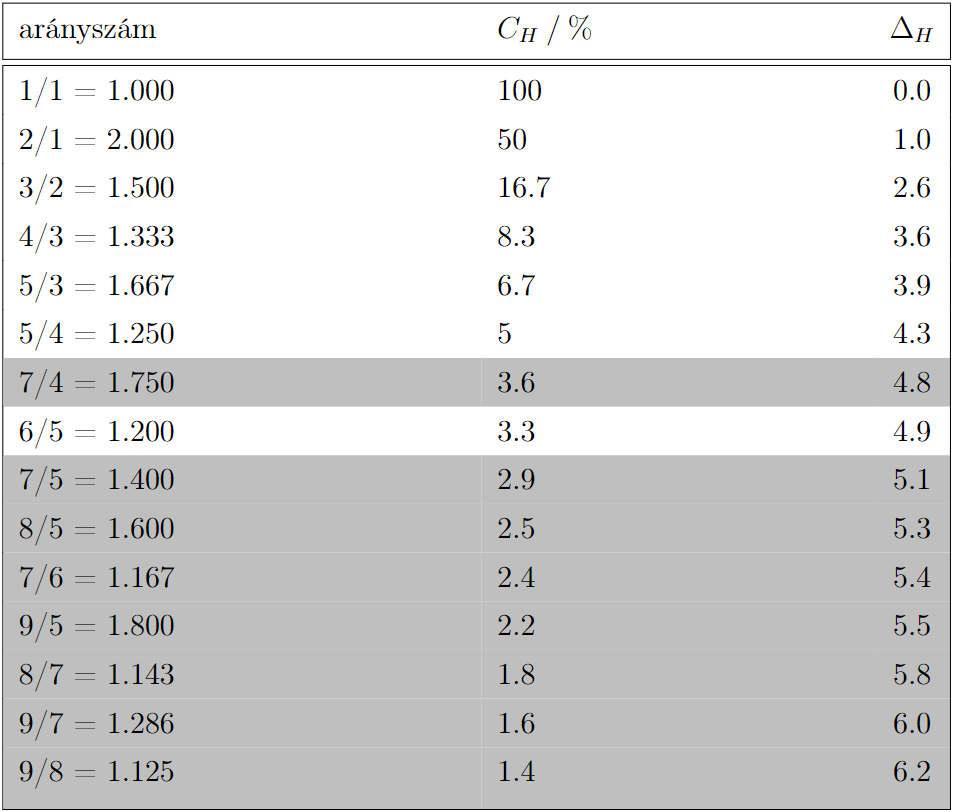
1. táblázat: Helmholtz táblázata az egy oktávon belüli fő felhangarányokról és a megfelelő hangközök elhangoltságából adódó lebegések relatív erősségéről ( %-ban). A jobb oldali
%-ban). A jobb oldali  oszlop a
oszlop a 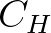 mennyiség reciprokának értékét méri logaritmikus skálán, így nincs dimenziója. A felhangsor hetedik vagy későbbi felhangjait tartalmazó arányok sorai szürkék.
mennyiség reciprokának értékét méri logaritmikus skálán, így nincs dimenziója. A felhangsor hetedik vagy későbbi felhangjait tartalmazó arányok sorai szürkék.
Az 1. táblázatban a Helmholtz által vizsgált fontosabb felhangok arányát láthatjuk, valamint ezek erősségét. Ez a paraméter, amelyet Helmholtz a táblázat sorbarendezéséhez használ, a megfelelő hangközök elhangoltságából eredő relatív erősség, amely úgy kapható, hogy modellezzük a Corti-szervben képződő rezonancia erősségét. Ez a mennyiség a következő értékkel írható le:
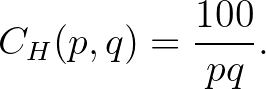
Helmholtz azt állította, hogy a hetedik felhang már nagyon halk a legtöbb hangszeren, és a távolabbi felhangoknak általában elhanyagolható a jelenléte. Így a hetedik vagy ennél magasabb felhangokat figyelmen kívül hagyva (ezek szürke sorok az 1. táblázatban) fönnáll a közelítési szabály, miszerint a hányados közvetlen kapcsolatban áll  értékével. Ezalól kivételt képez az
értékével. Ezalól kivételt képez az 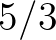 hányados. A táblázat kiegészült még egy oszloppal, amely inverz kapcsolatot mutat
hányados. A táblázat kiegészült még egy oszloppal, amely inverz kapcsolatot mutat 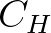 értékével logaritmikus skálán, így dimenzió nélküli mérőszám:
értékével logaritmikus skálán, így dimenzió nélküli mérőszám:
Melodikus távolság
A következő fejezetben bevezetünk egy zenészek által ugyan nem használt, azonban a konszonanciával és disszonanciával kapcsolatba hozható függvényt a frekvenciákon, így egyben a hangokon is.
A hallás, csakúgy, mint a többi érzékelés, az inger relatív változását érzékeli, különös tekintettel a 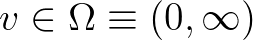 frekvenciáéra. Más megközelítéssel ahhoz, hogy mérni tudjuk a frekvencia változását, bevezetünk egy
frekvenciáéra. Más megközelítéssel ahhoz, hogy mérni tudjuk a frekvencia változását, bevezetünk egy 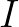 függvényt, amelyet a kövekező képlettel definiálunk:
függvényt, amelyet a kövekező képlettel definiálunk:
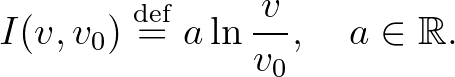
Az 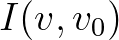 dimenziómentes mennyiség a
dimenziómentes mennyiség a 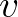 és egy tetszőleges
és egy tetszőleges 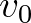 kezdőérték közötti frekvencia távolságát méri logaritmikus skálán. Feltéve, hogy a távolság egysége egy oktáv, azaz
kezdőérték közötti frekvencia távolságát méri logaritmikus skálán. Feltéve, hogy a távolság egysége egy oktáv, azaz 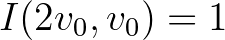 , adódik, hogy
, adódik, hogy 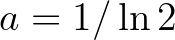 . Tehát a távolság két tiszta hang között a következő módon számolható:
. Tehát a távolság két tiszta hang között a következő módon számolható:
Ez az egyenlet leírja azt a természetes feltételezést is, hogy 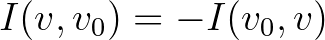 , tehát a távolságnak van előjele és iránya. Másrészről az így értelmezett távolság abszolút értéke az
, tehát a távolságnak van előjele és iránya. Másrészről az így értelmezett távolság abszolút értéke az  halmazbeli frekvenciák melodikus távolságát definiálja:
halmazbeli frekvenciák melodikus távolságát definiálja:
Egy adott 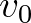 értékre a távolságfüggvény és a melodikus távolság a frekvenciák (általánosságban frekvenciaarányok)
értékre a távolságfüggvény és a melodikus távolság a frekvenciák (általánosságban frekvenciaarányok) 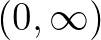 intervallumában definiáltak, és értéküket az előbbi esetben a hangmagasságok közti távolságok mérésére az
intervallumában definiáltak, és értéküket az előbbi esetben a hangmagasságok közti távolságok mérésére az 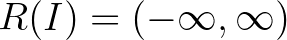 intervallumból, az utóbbi esetben pedig az
intervallumból, az utóbbi esetben pedig az 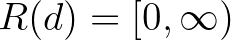 intervallumból veszik föl.
intervallumból veszik föl.
Feltehető, hogy az alapfrekvencia az 1 egység. Ekkor az alaphang és egy  frekvenciához tartozó hang távolságát a következőképpen írhatjuk le:
frekvenciához tartozó hang távolságát a következőképpen írhatjuk le:
Hasonlóan 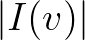 az alaphang és a
az alaphang és a 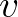 frekvenciához tartozó hang melodikus távolsága. Mivel a távolságunknál az egységhossz egy oktáv, ezért a távolság értékének egészrésze,
frekvenciához tartozó hang melodikus távolsága. Mivel a távolságunknál az egységhossz egy oktáv, ezért a távolság értékének egészrésze,
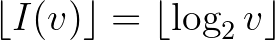
mutatja, hogy hány oktávnyira helyezkedik el a 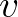 frekvenciához tartozó hang az alaphanghoz képest.
frekvenciához tartozó hang az alaphanghoz képest.
A (4) egyenletben leírt jelölést és a logaritmus azonosságait két frekvencia szorzatára használva teljesül, hogy
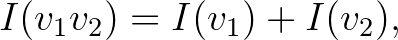
valamint a (2) egyenlet kifejezhető úgy, mint
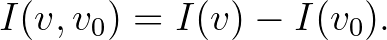
Például a 12 fokú kiegyenlített hangolású skála hangjai egy oktávon belül az 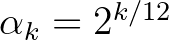 ;
; 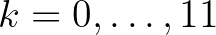 frekvenciákat adják. Ez egy mértani sorozat, és az
frekvenciákat adják. Ez egy mértani sorozat, és az 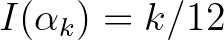 melodikus távolságaik pedig egy számtani sorozatot alkotnak. A bevezetett távolságfogalmunknak ezen tulajdonsága is egybevág a zenei szemléletmóddal, vagyis hogy egy kiegyenlített hangolású hangsor hangjai egyenlő távolságra vannak egymástól.
melodikus távolságaik pedig egy számtani sorozatot alkotnak. A bevezetett távolságfogalmunknak ezen tulajdonsága is egybevág a zenei szemléletmóddal, vagyis hogy egy kiegyenlített hangolású hangsor hangjai egyenlő távolságra vannak egymástól.
Relatív prím felhangok közti távolság
Ebben a fejezetben bevezetünk egy zenészek által ugyan nem használt, a matematikai távolság fogalmának azonban eleget tevő függvényt, amelyet először csak egymáshoz képest relatív prím frekvenciájú felhangokon értelmezünk. (Vegyük észre, hogy tisztán intonált hangközként hat az alaphang és egy felhangja, hiszen frekvenciaarányuk racionális. Éppen ezért a továbbiakban is az alaphanggal és felhangjaival fogunk számolni, erre értelmezünk távolságot.) Továbbá konstrukciót adunk a hanggráfra, amelyet mint geometriai szemléltetőeszközt arra fogunk használni, hogy kapcsolatba hozzuk az egyazon alaphanghoz tartozó két felhang közötti disszonanciát a melodikus távolsággal.
Szeretnénk összehasonlítani egy adott 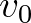 frekvenciához tartozó alaphang két felhangját:
frekvenciához tartozó alaphang két felhangját:
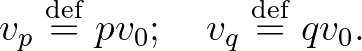
Először feltesszük, hogy 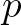 és
és 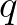 pozitív egészek és egymáshoz képest relatív prímek. Tehát legnagyobb közös osztójuk
pozitív egészek és egymáshoz képest relatív prímek. Tehát legnagyobb közös osztójuk 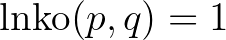 és legkisebb közös többszörösük
és legkisebb közös többszörösük 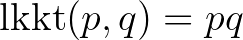 . Ekkor a legkisebb
. Ekkor a legkisebb  és
és 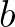 természetes számok, amelyekre teljesül, hogy
természetes számok, amelyekre teljesül, hogy 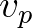 egy felhangja megegyezik
egy felhangja megegyezik 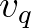 egy felhangjával, azaz
egy felhangjával, azaz
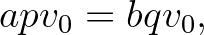
az nyilvánvalóan az  és
és 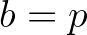 . A fenti meggondolás alapján értelmezzük
. A fenti meggondolás alapján értelmezzük 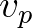 és
és 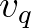 legmélyebb közös felhangját (lmkf) mint:
legmélyebb közös felhangját (lmkf) mint:
A melodikus távolság tehát egy 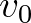 alaphang és két felhangjának a legmélyebb közös felhangja között a (3) és (4) egyenletek alapján:
alaphang és két felhangjának a legmélyebb közös felhangja között a (3) és (4) egyenletek alapján:
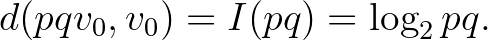
Most megépítjük a 2. ábrán látható irányított hanggráfot. A csúcsokban frekvenciák állnak, amelyeket az éleken feltüntetett arányuk szerint kötünk össze. Egy csúcsból az alatta lévő szintre mutat egy  -él az egyik irányba és egy
-él az egyik irányba és egy  -él a másikba. Ezt a gráfot távolságmérésre fogjuk használni.
-él a másikba. Ezt a gráfot távolságmérésre fogjuk használni.
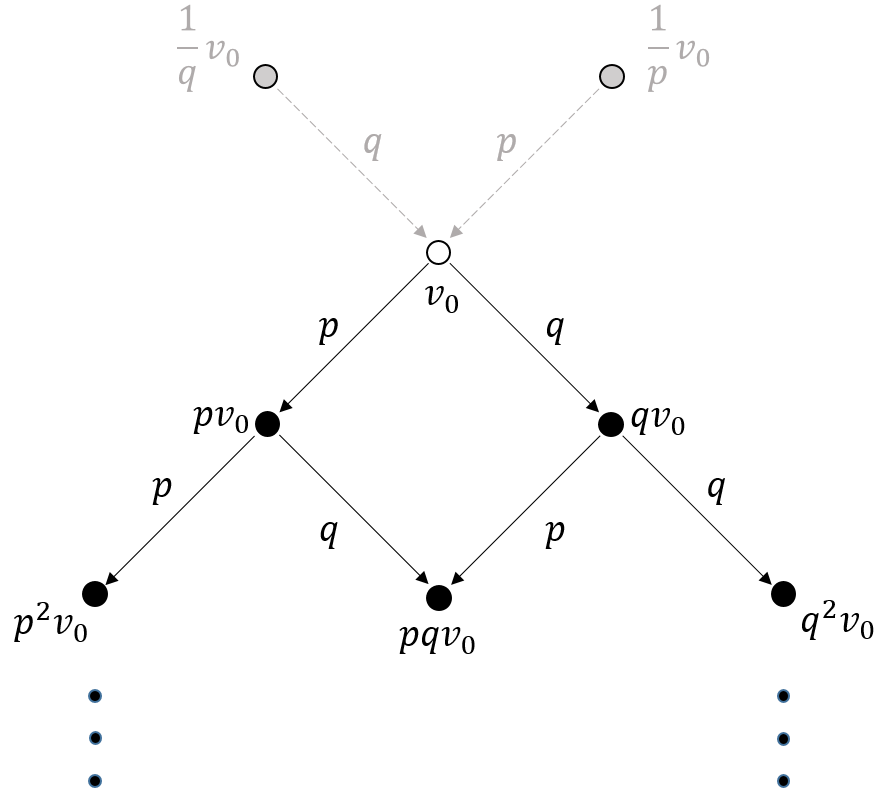
2. ábra: 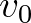 gyökerű hanggráf, melynek élein a
gyökerű hanggráf, melynek élein a 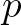 és
és 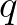 relatív prím frekvenciák állnak.
relatív prím frekvenciák állnak. 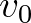 felmenői szürkék.
felmenői szürkék.
A 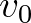 csúcsból indulunk. A
csúcsból indulunk. A 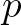 irány mentén haladva elérjük a
irány mentén haladva elérjük a 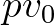 ,
, 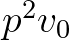 stb. pontokat, a
stb. pontokat, a 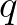 irány mentén pedig a
irány mentén pedig a 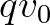 ,
, 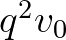 stb. pontokat. Általában tehát a
stb. pontokat. Általában tehát a 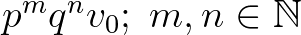 frekvenciáknak megfelelő felhangok állnak a gráf csúcsaiban. A melodikus távolság két szomszédos pont között
frekvenciáknak megfelelő felhangok állnak a gráf csúcsaiban. A melodikus távolság két szomszédos pont között 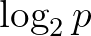 , ha egy
, ha egy 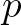 -éllel vannak összekötve, és
-éllel vannak összekötve, és 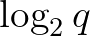 , ha egy
, ha egy 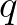 -éllel.
-éllel.
A 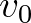 csúcsból a
csúcsból a 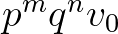 csúcsba bármilyen útvonalon eljuthatunk, amely
csúcsba bármilyen útvonalon eljuthatunk, amely 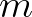 darab
darab 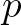 -élt és
-élt és 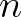 darab
darab 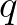 -élt tartalmaz a sorrendtől eltekintve. Ezen útvonal melodikus hossza
-élt tartalmaz a sorrendtől eltekintve. Ezen útvonal melodikus hossza
amely egyenként kiszámolható a közös 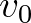 kezdőcsúcsból
kezdőcsúcsból 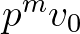 -ba és
-ba és 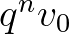 -ba menő távolságok összegeként. Irányított körmentes gráfokban ez a közös kezdőcsúcs a gyökér, amely itt a legmagasabb közös alhangnak felel meg (lmka). Ez az első olyan csúcs a
-ba menő távolságok összegeként. Irányított körmentes gráfokban ez a közös kezdőcsúcs a gyökér, amely itt a legmagasabb közös alhangnak felel meg (lmka). Ez az első olyan csúcs a 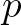 - és
- és 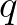 -élekkel címkézett hanggráfban, amelynek van
-élekkel címkézett hanggráfban, amelynek van 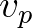 és
és 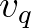 leszármazottja is. Így
leszármazottja is. Így
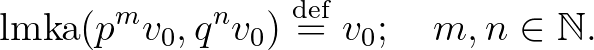
Vegyük észre, hogy a 2. ábra minden csúcsának közös osztója a legmagasabb közös alhang. Ennél fogva a korábban bevezetett távolságfogalom és műveleti tulajdonságai érvényesek maradnak, ha a legmagasabb közös alhangot választjuk egységnek.
Következésképpen minden 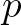 és
és 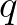 relatív prímre (de ez igaz marad minden
relatív prímre (de ez igaz marad minden 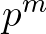 és
és 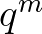 prímhatvány esetén is) a harmonikus távolság a
prímhatvány esetén is) a harmonikus távolság a 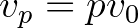 és
és 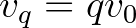 frekvenciákhoz tartozó hangok között úgy definiálható, mint a hangok legmélyebb közös felhangjának a legmagasabb közös alhangjától vett melodikus távolsága:
frekvenciákhoz tartozó hangok között úgy definiálható, mint a hangok legmélyebb közös felhangjának a legmagasabb közös alhangjától vett melodikus távolsága:
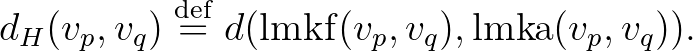
Amint azt a (6) egyenletnél is írtuk, ez megegyezik az 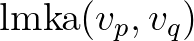 legmagasabb közös alhang
legmagasabb közös alhang  és
és  csúcstól mért melodikus távolságának összegével:
csúcstól mért melodikus távolságának összegével:
Minden 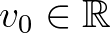 alapfrekvencia esetén a harmonikus távolság két felhangra:
alapfrekvencia esetén a harmonikus távolság két felhangra:
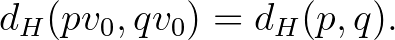
Ez az érték a hanggráfon lévő távolság a két frekvencia közös alaphangja és legmélyebb közös felhangja között.
Tetszőleges felhangok közti távolság
A következő fejezetben általánosítjuk az előbb bevezetett távolságfogalmat tetszőleges felhangok esetére, majd belátjuk, hogy egy alaphang immáron összes felhangján értelmezett függvény valóban metrika.
Most összehasonlítjuk egy 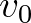 frekvenciához tartozó alaphang két nem relatív prím felhangját. Ezek legyenek
frekvenciához tartozó alaphang két nem relatív prím felhangját. Ezek legyenek
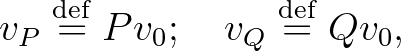
ahol 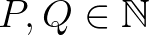 , és
, és
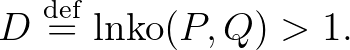
Az előző fejezet jelöléseivel élve 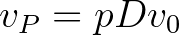 és
és  , ahol
, ahol 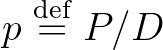 és
és 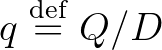 relatív prímek, mert ha nem lennének, akkor
relatív prímek, mert ha nem lennének, akkor 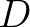 sem lehetne
sem lehetne 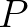 és
és 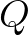 legnagyobb közös osztója. Ismeretes, hogy
legnagyobb közös osztója. Ismeretes, hogy
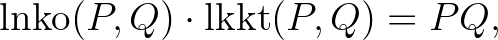
azaz
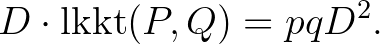
Leosztva az egyenlet mindkét oldalát 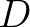 -vel:
-vel:
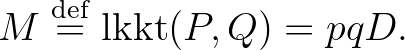
Ezek után az (5) egyenlethez hasonlóan értelmezhetjük a legmélyebb közös felhangot mint
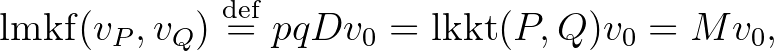
valamint a legmagasabb közös alhangot mint
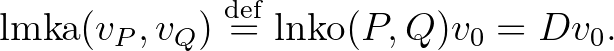
Ezzel a 2. ábrához hasonló szerkezetű gráfot kapunk, de most a közös kezdőcsúcs 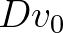 . Ebből már könnyen adhatunk képletet két tetszőleges felhang harmonikus távolságának kiszámítására. Hasonlóan a (7) egyenletben felírtakhoz,
. Ebből már könnyen adhatunk képletet két tetszőleges felhang harmonikus távolságának kiszámítására. Hasonlóan a (7) egyenletben felírtakhoz, 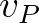 és
és 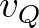 harmonikus távolsága a legmagasabb közös alhangjuknak a legmélyebb közös felhangjuktól vett melodikus távolságával definiálható:
harmonikus távolsága a legmagasabb közös alhangjuknak a legmélyebb közös felhangjuktól vett melodikus távolságával definiálható:
Következésképpen igaz az alábbi egyenlőséglánc:
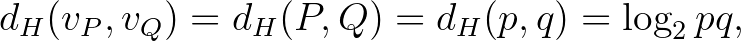
vagyis tetszőleges nem relatív prím felhangok harmonikus távolsága visszavezethető relatív prímekére azáltal, hogy a legkisebb közös többszöröst leosztjuk a legnagyobb közös osztóval, és a megmaradt relatív prímek harmonikus távolságát mérjük. Tehát a harmonikus távolságra adható másik definíció:
amely minden  alaphang esetén fenáll.
alaphang esetén fenáll.
A harmonikus távolság valóban távolságot definiál, ugyanis kielégíti a metrika axiómáit.
Nemnegativitás és nullhossz: a (8) egyenlet miatt 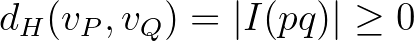 nyilvánvalóan. Továbbá
nyilvánvalóan. Továbbá
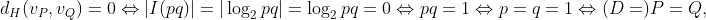
ahol kihasználtuk, hogy 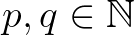 .
.
Szimmetria: a (9) egyenlet miatt
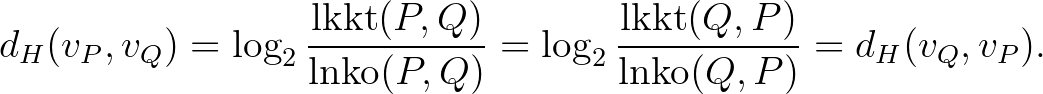
Háromszög-egyenlőtlenség: Legyen 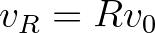 , ahol
, ahol 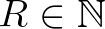 . Kellene:
. Kellene:
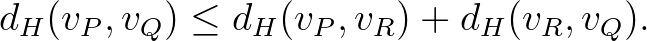
Ez a (9) egyenlet alapján átalakítva:
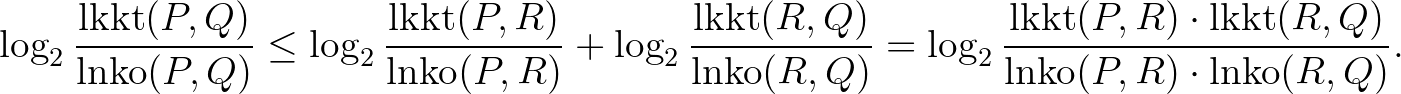
Vizsgáljuk meg külön a számlálót és a nevezőt!
Számláló: Két szám legkisebb közös többszörösét úgy keressük, hogy a számok prímtényezős felbontásaiból a nagyobb hatványon kiválasztjuk a prímeket, majd ezeket összeszorozzuk. Ez alapján a jobb oldali számláló valóban nem lehet kisebb a bal oldalinál, hiszen 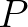 és
és 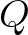 prímtényezőit most is kiválasztjuk legalább ugyanakkora hatványon, ezen felül
prímtényezőit most is kiválasztjuk legalább ugyanakkora hatványon, ezen felül 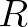 miatt kerülhet be még szorzótényező.
miatt kerülhet be még szorzótényező.
Nevező: Két szám legnagyobb közös osztójának megtalálásához a közös prímtényezőket szorozzuk össze a kisebb hatványon. Öt esetet különíthetünk el:
1. Egy prím 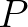 -nek és
-nek és 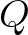 -nak közös prímtényezője, és ez nem osztója
-nak közös prímtényezője, és ez nem osztója 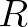 -nek: ezzel a bal oldalon osztunk, a jobb oldalon azonban nem, így a jobb oldal nagyobb vagy egyenlő marad.
-nek: ezzel a bal oldalon osztunk, a jobb oldalon azonban nem, így a jobb oldal nagyobb vagy egyenlő marad.
2. Egy prím 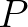 -nek és
-nek és 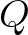 -nak közös prímtényezője, és ez osztója
-nak közös prímtényezője, és ez osztója 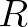 -nek is: könnyen meggondolható, hogy ez a prím a jobb oldali számláló egyik kifejezésében előfordul legalább akkora hatványon, mint a bal oldaliban; és a jobb oldali nevező egyik kifejezésében előfordul legfeljebb akkora hatványon, mint a bal oldaliban. Tehát a jobb oldalon összességében biztosan nagyobb hatványon szerepel ez a prím.
-nek is: könnyen meggondolható, hogy ez a prím a jobb oldali számláló egyik kifejezésében előfordul legalább akkora hatványon, mint a bal oldaliban; és a jobb oldali nevező egyik kifejezésében előfordul legfeljebb akkora hatványon, mint a bal oldaliban. Tehát a jobb oldalon összességében biztosan nagyobb hatványon szerepel ez a prím.
3. Egy prím 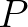 -nek és
-nek és 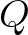 -nak nem közös prímtényezője,
-nak nem közös prímtényezője, 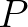 -nek és
-nek és 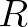 -nek azonban az (ez
-nek azonban az (ez 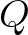 -nak és
-nak és 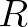 -nek biztosan nem közös prímtényezője, mert akkor
-nek biztosan nem közös prímtényezője, mert akkor 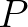 -nek és
-nek és 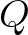 -nak is az lenne): ez a prímtényező a bal oldalon csak a számlálóban szerepel; a jobb oldali számláló mindkét kifejezésében megjelenik, ráadásul legalább az egyikben nem kisebb hatványon. A jobb oldali nevezőben pedig legfeljebb akkora hatványon lesz jelen, mint a számlálóban a kisebb. Tehát most is a jobb oldal nagyobb vagy egyenlő.
-nak is az lenne): ez a prímtényező a bal oldalon csak a számlálóban szerepel; a jobb oldali számláló mindkét kifejezésében megjelenik, ráadásul legalább az egyikben nem kisebb hatványon. A jobb oldali nevezőben pedig legfeljebb akkora hatványon lesz jelen, mint a számlálóban a kisebb. Tehát most is a jobb oldal nagyobb vagy egyenlő.
4. Egy prím 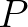 -nek és
-nek és 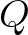 -nak nem közös prímtényezője,
-nak nem közös prímtényezője, 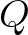 -nak és
-nak és 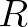 -nek azonban az: ugyanúgy, mint az előző esetben.
-nek azonban az: ugyanúgy, mint az előző esetben.
5. A három számnak nincs közös prímosztója: mindenhol 1-gyel osztunk, így a jobb oldal nagyobb, mivel a számlálót már vizsgáltuk.
Vegyük észre, hogy 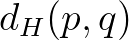 értéke megegyezik az (1) egyenletben definiált
értéke megegyezik az (1) egyenletben definiált 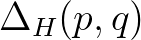 kifejezéssel, amellyel az 1. táblázat jobb oldali oszlopának értékeit számítottuk ki. Tehát találtunk egy matematikai mennyiséget, nevezetesen a harmonikus disszonanciát, amellyel a felhangok távolságát, zeneileg a tisztán intonált hangközök hallatán érzett disszonanciát tudjuk mérni.
kifejezéssel, amellyel az 1. táblázat jobb oldali oszlopának értékeit számítottuk ki. Tehát találtunk egy matematikai mennyiséget, nevezetesen a harmonikus disszonanciát, amellyel a felhangok távolságát, zeneileg a tisztán intonált hangközök hallatán érzett disszonanciát tudjuk mérni.
Megjegyzés
Szerzőnk idén kezdi meg MSc tanulmányait, szakdolgozatát ebből a nem mindennapi témából írta. Aki a fenti ízelítő után további érdekességeket szeretne megtudni, olvassa el a teljes szakdolgozatot. (Szerk.)
Lábjegyzet
- 1 Hermann Ludwig Ferdinand von Helmholtz, 1821–1894: orvos, fizikus; az emberi látás és hallás tudományos tanulmányozásának úttörője.
Definíciók
Konszonancia: két vagy több hang egyidejű, folytatásra nem szoruló, kellemes hatást keltő, harmonikus megszólalása. Magyarul összehangzás, összhang.
Disszonancia: hangoknak olyan együtthangzása, amelyet a fül a megszokott összhangzattal ellentétesnek, kellemetlennek, érdesnek érez, s amely feloldást kíván. Magyarul széthangzás.
Hangköz: két zenei hang távolsága, hangmagasságuk egymáshoz való viszonya, amelyet a két hang frekvenciaaránya fejez ki.
Tiszta intonáció: az összes zenei hangköz a frekvenciák egész számarányaira (például 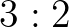 vagy
vagy 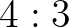 ) hangolva.
) hangolva.
Oktáv: a latin octava - nyolcadik szóból származik; egy hanghoz tartozó frekvencia dupláját jelenti.
Tiszta hang: olyan hang, amelynek nyomása az időben a szinuszfüggvénynek megfelelően változik. A mindennapi életben tiszta hang csak kivételesen fordul elő.
Alaphang: a zenei hang fülünk által érzékelt hangmagassága. Az alaphang frekvenciája az alapfrekvencia.
Felhang: együtt hangzó hang, amely egy zenei hang megszólaltatásakor az alaphanggal együtt szól, azt színezi. Ez a rezgő test egy-egy szakaszának (felének, harmadának, negyedének) külön-külön rezgésével keletkező magasabb hangok közül egy. A felhangok frekvenciái az alapfrekvencia egész számú többszörösei (ezért speciálisan az alaphang önmaga felhangja).
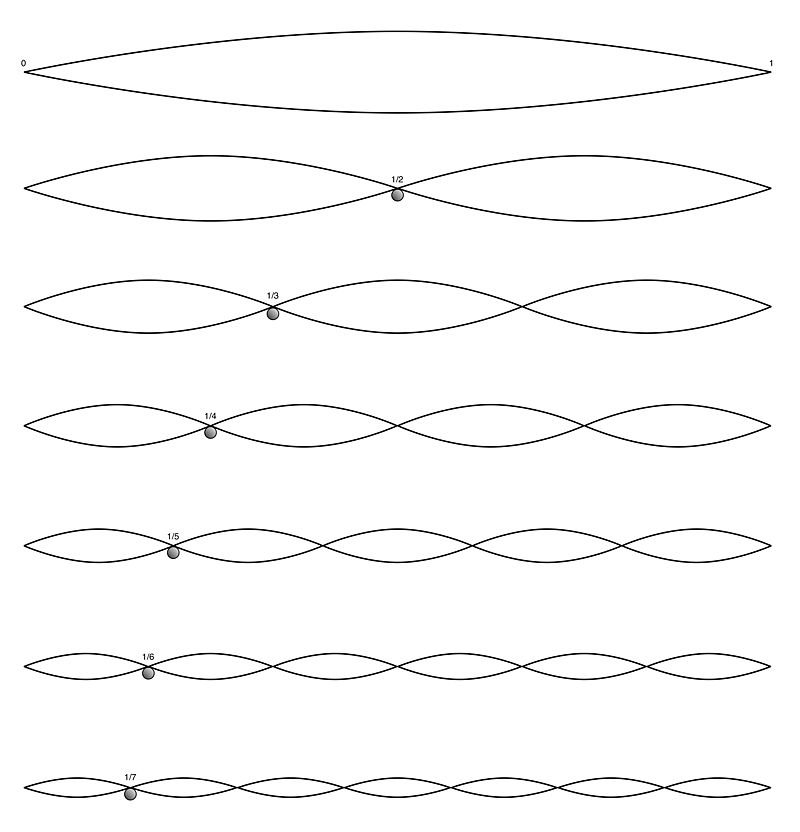
Különböző felhangok megszólalása húron a megfelelő osztópontoknál. Forrás: https://hu.wikipedia.org/wiki/Felhangsor
Alhang: olyan hang, amely frekvenciájának egész számú többszöröse az alaphang.
Felhangsor: egy zenei hang részhangjainak sorozata. Ha az alapfrekvencia 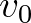 , akkor a felhangsor a
, akkor a felhangsor a 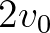 ,
, 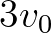 ,
, 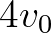 stb. frekvenciák sorozata.
stb. frekvenciák sorozata.
Hangsor vagy skála: valamely dallam hangjainak magasságuk szerint rendezett sora. A hangsor foka mondja meg, hány hangból áll a skála.
Kiegyenlített hangolás: az oktáv matematikailag pontosan egyenlő nagyságú hanglépésekre való felosztásával nyert hangolás. Az európai zenében a 12 fokú kiegyenlített hangolású hangsor használatos, pl.: gitár, zongora hangolása.