A szegedi Acta 100 éve

Tavaly ünnepelte fennállásának 100. évfordulóját az Acta Scientiarum Mathematicarum, vagy ahogy röviden hívni szokták: a szegedi Acta folyóirat. Ebben a cikkben rövid áttekintést adunk ennek a világ 20 legrégebbi és ma is aktív matematikai periodikája közé tartozó folyóiratnak a múltjáról és jelenéről.

1. Rövid történeti áttekintés

Az 1870-es években felvetődött a már létező budapesti és kolozsvári egyetemek mellé egy harmadik tudományegyetem alapítása a Magyar Királyságban. Pozsony és Szeged erős versengést folytatott az új egyetem befogadásáért. Az 1879-es, Szegedet szinte teljesen elpusztító hatalmas árvíz után a város romjaiból újjáépült, gyönyörű várossá változott. A közvélemény és számos szaktekintély határozottan támogatta egy itteni egyetem létrehozásának gondolatát. Végül azonban Pozsony, az egykori koronázóváros járt sikerrel, 1912-ben ott alapították meg a harmadik egyetemet. Sőt, ugyanabban az évben megalakult a negyedik egyetem is, mégpedig Debrecenben.

Szeged tehát elvesztette az egyetemért vívott küzdelmet, de a történelem hamarosan közbeszólt. Az első világháború után az 1920-as trianoni békeszerződés átszabta Magyarország térképét, és Kolozsvár Románia része lett. Az egyetem oktatói nem voltak hajlandók a román király iránti hűségesküt letenni, ezért az egyetemnek el kellett költöznie. Klebelsberg Kuno későbbi vallás- és közoktatásügyi miniszter szorgalmazta az egyetem áthelyezését Kolozsvárról Szegedre. (Szeged a háború utáni Magyarország határvárosává vált.) A terv megvalósult, és 1921-ben a kolozsvári egyetem Szegedre települt át.

Haar Alfréd és Riesz Frigyes, akkoriban már világhírű kolozsvári tudósok és egyetemi tanárok szintén Szegedre költöztek, és megalapították az ottani matematikai iskolát.


Haar Alfréd	Riesz Frigyes

A színvonalas kutatás feltételeinek megteremtése érdekében igényes matematikai könyvtárat kívántak létrehozni, mivel a kolozsvári könyvtárat hátra kellett hagyni. A rendelkezésre álló (korlátozott) anyagi források és alkalmi adományok – köztük a Rockefeller Alapítvány nagylelkű támogatása – mellett felmerült a gondolat, hogy létrehoznak egy tekintélyes matematikai folyóiratot, amely cserealapot szolgáltat más folyóiratok beszerzéséhez, megteremtve ezzel a könyvtár stabil és szilárd hátterét. Ilyen körülmények között indították útjára 1922-ben a szegedi Acta-t.

A folyóirat neve az idők során többször változott. Elsőként Acta Literarum ac Scientiarum Regiae Universitatis Hungariae Francisco Josephinae, Sectio Scientiarum Mathematicarum-nak; később Acta Universitatis Szegediensis, Sectio Scientiarum Mathematicarum-nak nevezték. A második világháború után ismét névváltozás történt: előbb Acta Scientiarum Mathematicarum (Szeged), majd Acta Universitatis Szegediensis, Acta Scientiarum Mathematicarum lett az elnevezése.

Az első kötet borítója

Haar és Riesz cserékre vonatkozó terve kiválóan működött. A cserekezdeményezések némelyike jól dokumentált, a következőket [3]-ból idézzük. „Riesz 1922. december 12-én írt Maurice Fréchet-nek, és elküldte neki a szegedi Acta első fakszimiléjét, hogy népszerűsítse azt (Riesz 1922). Fréchet válaszára nem kellett sokat várni. 1922. december 16-án azt írta, hogy számukra »megtiszteltetés lenne« megkapni a szegedi Acta-t, és cserébe felajánlotta Riesznek a Publications de l'Institut de Mathematiques de l'Université de Strasbourg nevű folyóiratot, valamint a Strasbourgi Egyetem Matematikai Intézetében elkészült doktori értekezések másolatait. (…) G.H. Hardy 1922-ben írt Riesznek a szegedi Acta cseréjével kapcsolatban (Hardy 1922), továbbá három levél lelhető fel ugyanerről a témáról a Gösta Mittag-Lefflerrel (Svédország) 1923 és 1924 között folytatott levelezésben (Mittag-Leffler 1923, 1924).”

A kezdeti cserekapcsolatok sikere minden bizonnyal Riesz nemzetközi matematikai közösségben elfoglalt magas tudományos pozíciójának volt köszönhető. De Haar és Riesz nem akartak kizárólag erre támaszkodni, hanem magát a folyóiratot kívánták vonzóvá tenni, ezért felkértek több vezető matematikust a szegedi Acta-ban való publikálásra. Ezek a próbálkozások is rendkívül sikeresek voltak. Az első évek szerzőinek listáján többek között olyan matematikusok nevét találjuk, mint Neumann János, Norbert Wiener, George D. Birkhoff, Henri Cartan, Antoni Zygmund, Fejér Lipót, Pólya György, vagy Szegő Gábor. Ez jelentősen hozzájárult ahhoz a sikerhez, amelyet E. R. Lorch így írt le [2]: „A szegedi Acta néhány éven belül világhírnévre tett szert. Minden komoly matematikai könyvtárba jár. Ezért Szegedet ma már az egész világon ismerik – legalábbis a matematikusok.” Ezzel egybehangzóan Staar Gyula magyar tudományos újságíró azt írta az [5] gyűjteményben, hogy „Szeged hamarosan matematikai kutatóközponttá vált, és Szegedet sokan a mai napig a magyar Göttingennek nevezik.” Megjegyezzük, hogy már Klebelsberg Kuno is előszeretettel nevezte Pécset (ahová a trianoni békeszerződés után a pozsonyi egyetem költözött) „magyar Heidelberg”-nek, Szegedet pedig „magyar Göttingá”-nak.

Egy érdekes történetet idézünk az [1]-ből, amely jól mutatja, hogy Riesz Frigyes mennyire igényes volt a folyóiratukban megjelenő közlemények minőségét illetően. „Anekdota a Riesz fivérekről, amit Szőkefalvi-Nagy Bélától és Horváth Jánostól hallottunk. (Horváth régi barátja és munkatársa volt Riesz Marcelnek.) Marcel egyszer benyújtott egy cikket a szegedi Acta-hoz, ahol Frigyes alapító és szerkesztő volt. Minden bizonnyal jó cikk volt, de Frigyes azt írta öccsének: 'Marcel, írtál te már jobbakat is.' Az igazsághoz tartozik, hogy Marcel tényleg publikált a szegedi Acta-ban.” Valóban, a folyóirat első két kötetében négy cikket is közölt.

A szegedi Acta cseréje igazi siker volt, és a harmincas évekre a szegedi matematikai intézet könyvtára rendelkezett Magyarország legkiterjedtebb matematikai folyóirat-gyűjteményével. Kiemelendő, hogy az 1930-as évektől nemcsak a szegedi Acta kezdeményezett ilyen jellegű cseréket, hanem számos hasonló megkeresést és ajánlatot is kapott. Egy dokumentum szerint 1948 és 1965 között 178 volt a cserék száma. A hosszú listából 10 folyóirat nevét említjük: Acta Math., Amer. J. Math., Ann. Math., Canad J. Math., Duke J. Math., J. London Math. Soc., Math. Ann., Proc. Cambridge Math. Soc., Proc. London Math. Soc., Trans. Amer. Math. Soc.

A folyóiratcserék mellett több kiadó küldött könyveket a szegedi Acta-ban való ismertetésre, amelyek a folyóiratban megjelent recenzió ellenértékeként a könyvtár tulajdonába kerültek ezzel is gyarapítva annak állományát.

Haar Alfréd 1933-ban elhunyt, Riesz Frigyes 1946-ban Budapestre költözött. 1946-tól 1981-ig Szőkefalvi-Nagy Béla (vezetéknevét a nemzetközi tudományos világban általában Sz.-Nagynak rövidítik), az operátorelmélet vezető tudósa volt a főszerkesztő. A Haar és Riesz által kialakított hagyományokat folytatta, különös gonddal és odaadással intézte a folyóirat ügyeit. Lánya, Erzsébet (Szőkefalvi-Nagy Béla és felesége hat gyermeket neveltek fel) elmondása szerint a családban a szegedi Acta-t Szőkefalvi-Nagy Béla hetedik gyermekeként emlegették. Hosszú, 35 éves főszerkesztői tevékenysége alatt a szegedi Acta továbbra is nagy tekintélyű folyóirat volt, a funkcionálanalízis és az operátorelmélet nemzetközileg vezető folyóiratává vált.

Szőkefalvi-Nagy Béla mellett, aki maga is 65 közleményt publikált a szegedi Acta-ban, az említett két tudományterület számos kiemelkedő kutatója jelentetett meg nagy hatású munkákat a folyóiratban. Többek között T. Ando, H. Bercovici, A. Connes, Ch. Davis, J. Dieudonné, J. Dixmier, R. Douglas, N. Dunford, C. Foias, I. Gohberg, P. Halmos, W. Helton, M. G. Krein, H. Langer, M. A. Naimark, H. Radjavi, D. Sarason, D. Voiculescu, és a lista még hosszan lenne folytatható.

Szőkefalvi-Nagy Béla után a következő főszerkesztők Leindler László (1982–1992 között) és Kérchy László (1993–2017 között) voltak.

1999-ben, egy évvel Szőkefalvi-Nagy Béla halála után, lánya, Erzsébet édesapja emlékére megalapította a Szőkefalvi-Nagy Béla Érmet. Ezzel a díjjal olyan jeles matematikusokat tüntetnek ki, akik jelentős műveket publikáltak a szegedi Acta-ban. (A kitüntetésben részesültek névsora itt található.)

2. A szegedi Acta-ban megjelent néhány nagyhatású cikk

A fentiek után nem meglepő, hogy a folyóirat számos fontos, nagy hatású közleményt publikált története során. Ebben a részben ezek közül mutatunk be egy tucatnyit.

Neumann János egy dolgozatával kezdjük, amely az első kötetben jelent meg.

J. von Neumann, Zur Einführung der transfiniten Zahlen, Acta Sci. Math. (Szeged), 1 (1922–23), 199–208.

A rendszámokat a nemnegatív egész számok transzfinit változataiként már a halmazelmélet kezdeteitől fogva használták, de ezek „külső objektumok” voltak, ami kissé zavaró körülmény volt. A rendszámokkal szemben támasztott alapkövetelmény, hogy minden jólrendezett halmazhoz rendelődjön rendszám, és az egymással izomorf jólrendezett halmazokhoz ugyanaz a rendszám tartozzon. A fenti írásban az akkor 19 éves Neumann János bevezette a rendszámoknak azt a fogalmát, amelyet a mai napig használnak.

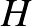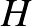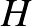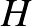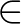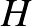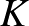Egy $H$ halmaz rendszám, ha $H$ tranzitív (vagyis $H$ minden eleme egyben részhalmaza is $H$ -nak), és az $\in$ (eleme) reláció jólrendezés $H$ -n. A $K$ rendszámot kisebbnek mondjuk 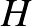$H$ -nál, ha 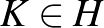$K\in H$ . Ez a rendszámoknak egy jólrendezését adja, és minden rendszám megegyezik a nála kisebb rendszámok halmazával.

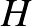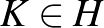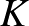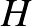Ezenkívül Neumann a rendszámok segítségével definiálta a számosság fogalmát is. Egy $H$ rendszám számosság, ha minden $K\in H$ -ra teljesül, hogy nem létezik szürjektív leképezés $K$ -ról $H$ -ra. Ezen az egyszerű módon fel lehet építeni a rendszámok és számosságok teljes elméletét.

A halmazelméletről áttérünk az algebra területére, két dolgozatot említünk.

M. Krasner és L. Kaloujnine, Produit Complet des groupes de permutations and problem d'extension de groupes. III. Acta Sci. Math. (Szeged) 14 (1951), 69–82.

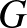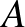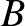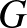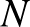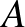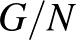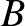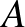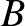Ebben a cikkben a szerzők bevezették a csoportok koszorúszorzatának fogalmát, és bebizonyították a következő alapvető tulajdonságát. Ha $G$ az $A$ csoport kiterjesztése a $B$ csoporttal abban az értelemben, hogy a $G$ -nek van olyan $N$ normális részcsoportja, amely izomorf $A$ -val és a $G/N$ faktorcsoport izomorf $B$ -vel, akkor az $A$ és $B$ koszorúszorzata tartalmazza a 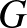$G$ egy izomorf képét. Ezt az eredményt Krasner–Kaluzsnyin vagy Kaluzsnyin–Krasner tételnek nevezik.

Bevezetése után, a csoportelmélettel foglalkozó matematikusok ezt a szorzatfogalmat többek között különféle ellenpéldák alkotására alkalmazták, illetve beágyazási tételek bizonyítására használták. A koszorúszorzat a csoportelmélet egyik fő eszközévé vált.

A másik algebra dolgozat hálóelmélettel foglalkozik.

G. Grätzer and E. T. Schmidt, Characterizations of congruence lattices of abstract algebras, Acta Sci. Math. (Szeged) 24 (1963), 34–59.

Ez a cikk tartalmazza az úgynevezett Grätzer–Schmidt tételt, amely szerint az algebrai hálók (azaz a teljes, kompaktan generált hálók) pontosan azok, amelyek izomorfak egy absztrakt algebra összes kongruenciarelációjának hálójával. Az eredmény egy G. Birkhoff által 1948-ban felvetett kérdést válaszolt meg, és az univerzális algebra alapvető tételévé vált.

Egy geometria cikkel folytatjuk.

Á. Császár, A polyhedron without diagonals. Acta Univ. Szeged. Sect. Sci. Math. 13 (1949), 140–142.

A dolgozatot a következő – egy 1948-as magyarországi matematika versenyen hibásan kitűzött – probléma motiválta: Bizonyítsuk be, hogy a tetraéderen kívül nincs olyan poliéder, amelyben bármelyik két csúcsot él köt össze. Más szavakkal, az állítás az volt, hogy a tetraéder az egyetlen olyan poliéder, amelynek nincs átlója. Az állítás valóban igaz konvex poliéderekre. Ebben a cikkben azonban Császár Ákos példát adott olyan nemkonvex poliéderre, amelynek nincs átlója. Érdekes módon a cikk nem kapott különösebb figyelmet egészen Martin Gardner „Mathematical Games: On the remarkable Császár polyhedron and its applications in problem solving” című népszerűsítő tanulmányáig, amely 1975-ben jelent meg a Scientific American-ben. Jelenleg a Google kereső több ezer találatot ad a „Császár polyhedron” kifejezésre.

Most áttérünk az analízis területére, először is a potenciálelméletre.

O. D. Kellogg, Some notes on the notion of capacity in potential theory, Acta Sci. Math. (Szeged) 4 (1928–29), 1–5.

A rövid cikk a potenciálelmélet három alapvető tételét tartalmazza. Az első a harmonikus függvények úgynevezett általánosított maximumelve. A standard maximum elv azt mondja, hogy ha egy (korlátos) harmonikus függvény nemnegatív a 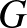$G$ tartomány határán, akkor ugyanez igaz az egész tartományon. Kellog azt vette észre, hogy alulról korlátos harmonikus függvények esetében a nemnegativitást nem szükséges a határ minden pontjában megkövetelni, elegendő az, ha a kivételes pontok halmaza nulla kapacitású.

Ami a második eredményt illeti, legyen 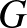$G$ egy tartomány, 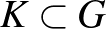$K\subset G$ pedig egy zárt halmaz. A megszüntethető szingularitások problémája harmonikus függvényekre a következőképpen fogalmazható meg: Milyen 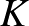$K$ halmazokra igaz, hogy a 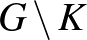$G\setminus K$ -n adott bármely korlátos harmonikus függvénynek van harmonikus kiterjesztése a teljes 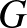$G$ tartományra? A cikkben Kellogg bebizonyította, hogy ez pontosan akkor igaz, ha a 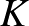$K$ kapacitása nulla.

A harmadik eredmény szerint, ha 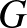$G$ egy tartomány, és 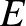$E$ a határának pozitív kapacitású részhalmaza, akkor 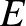$E$ szükségszerűen tartalmaz egy úgynevezett reguláris 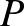$P$ pontot; azaz egy pontot azzal a tulajdonsággal, hogy ha a Dirichlet-probléma peremfeltételében lévő függvény folytonos 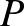$P$ -ben, akkor a Dirichlet-megoldás is folytonos 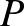$P$ -ben. Más szóval, az irreguláris pontok halmazának mindig nulla a kapacitása.

Az alábbi fotó a szegedi matematikai intézet egyik legértékesebb relikviája, amely G. D. Birkhoff és O. D. Kellog 1928-as szegedi látogatása során készült.

Felső sor: Riesz Frigyes, Kerékjártó Béla, Haar Alfréd, Kőnig Gyula, Ortvay Rudolf,
Középső sor: Kürschák József, George David Birkhoff, Oliver Dimond Kellog, Fejér Lipót,
Alsó sor: Radó Tibor, Lipka István, Kalmár László, Szász Pál.

A következő dolgozat, amelyet említünk, Riesz Frigyes fontos munkája a folyóirat első számából.

F. Riesz, Sur les valeurs moyennes du module des fonctions harmoniques et des fonctions analytiques, Acta Sci. Math. (Szeged) 1 (1922–23), 27–32.

Itt vezette be Riesz a szubharmonikus függvények fogalmát, és igazolta néhány alapvető tulajdonságukat. Maga a definíció egyszerű: A 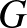$G$ tartományon definiált valós értékű folytonos függvényt szubharmonikusnak nevezzük, ha a 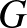$G$ bármely 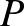$P$ pontjára és minden olyan 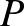$P$ körüli zárt körlapra, amely részhalmaza 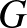$G$ -nek, az 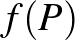$f(P)$ érték kisebb vagy egyenlő, mint 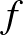$f$ integrálátlaga a körlap határolóköre mentén. A szubharmonikus függvények a modern potenciálelmélet központi objektumai.

Ezután két dolgozatot említünk a mértékelmélet/valószínűségszámítás területéről.

A. Prékopa, Logarithmic concave measures with application to stochastic programming, Acta Sci. Math. (Szeged) 32 (1971), 301–316.

A. Prékopa, On logarithmic concave measures and functions, Acta Sci. Math. (Szeged) 34 (1973), 335–343.

Jelenleg ez utóbbi a szegedi Acta-ban megjelent legtöbbet idézett cikk – a MathSciNet-en 162, a Google Scholar-ban pedig 732 hivatkozás található rá. Az előbbi dolgozatot is sokat idézik: 104 idézet a MathSciNet-en, 552 idézet a Google Scholar-ban.

A szerző, Prékopa András a sztochasztikus programozásnak nevezett terület egyik elindítója. Az itt elért fő eredményei közül több a valószínűségi korlátokat tartalmazó sztochasztikus programozási feladatok konvexitáselméletére, az ilyen problémák megengedett megoldásai halmazainak konvexitására vonatkozik. Ez a két dolgozat tartalmazza ennek az elméletnek a legalapvetőbb eredményeit. Ezekben vezette be Prékopa András a logaritmikusan konkáv mértékek fogalmát, és bizonyította a következőket.

(1) Ha a 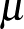$\mu$ Borel-mérték 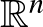$\mathbb{R}^n$ -en logkonkáv sűrűségfüggvényből származik, akkor 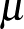$\mu$ logkonkáv, azaz minden 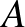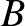$A$ , $B$ Borel-halmazra és minden 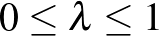$0\leq \lambda \leq 1$ valós számra teljesül, hogy

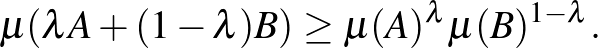
$\displaystyle \mu(\lambda A+(1-\lambda)B)\geq\mu(A)^\lambda\mu(B)^{1-\lambda}.$

(2) Ha egy többváltozós logkonkáv függvényt néhány változója szerint a teljes téren integrálunk, akkor a kapott többváltozós függvény is logkonkáv.

Ezek olyan áttörést jelentő eredmények, amelyek a valószínűségi korlátokat tartalmazó sztochasztikus programozási feladatok széles osztályára garantálják a megengedett megoldások halmazának konvexitását. Ezen következményeken túl a fenti eredmények a konvex geometriában, az analízisben, valamint a fizika, a statisztika és a közgazdaságtan egyes területein is alkalmazást nyertek.

Végül rátérünk az operátorelméletre, amely a folyóirat fő fókuszterülete volt Szőkefalvi-Nagy Béla idejében. Az ő néhány dolgozatával kezdjük.

B. Sz.-Nagy, On uniformly bounded linear transformations in Hilbert space, Acta Univ. Szeged. Sect. Sci. Math. 11 (1947), 152–157.

Ez Szőkefalvi-Nagy Béla legtöbbet idézett dolgozata, a MathSciNet-ben 88, a Google Scholar-ban 263 hivatkozás található rá jelenleg.

A cikk fő eredménye a következő alapvető tétel. Egy Hilbert-téren ható 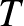$T$ invertálható korlátos (lineáris) operátor akkor és csak akkor hasonló egy unitér operátorhoz, ha a 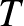$T$ összes egész hatványának halmaza egyenletesen korlátos; azaz korlátos halmazt alkot az operátor normában.

B. Sz.-Nagy, Sur les contractions de l'espace de Hilbert, Acta Sci. Math. (Szeged) 15 (1953), 87–92.

Ez az első része egy 12 cikkből álló, kontrakciókról szóló cikksorozatnak. Kontrakciónak nevezünk egy korlátos operátort, ha a normája legfeljebb 1. A kutatást az motiválta, hogy jobban megértsék a Hilbert-téren értelmezett általános lineáris operátorok szerkezetét. (Vegyük észre, hogy minden korlátos lineáris operátor egy kontrakció skalárszorosa).

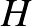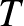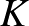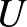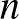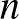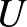
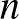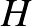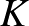Ebben a dolgozatban Szőkefalvi-Nagy Béla belátta, hogy a $H$ Hilbert-tér bármely $T$ kontrakciójához van egy nagyobb $K$ Hilbert-tér és rajta egy $U$ unitér operátor úgy, hogy bármely nemnegatív $n$ egész számra, $n$ -edik hatványa megegyezik $U$ $n$ -edik hatványa és $H$ -nak $K$ -ra történő ortogonális projekciója szorzatával:

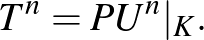
$\displaystyle T^n=P U^n\arrowvert_K.$

(Hasonlóan, 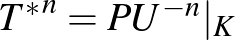${T^*}^n=P U^{-n}\arrowvert_K$ .) Az állítás rövid megfogalmazása: minden kontrakciónak létezik unitér hatványdilatációja. Ezen alapvető eredmény szerint általános operátort reprodukálni tudunk (bizonyos értelemben) két konkrét és jól ismert típusú operátorból: egy unitérből és egy ortogonális porjekcióból.

Mint fentebb említettük, ezt a munkát 11 másik, hasonló című dolgozat követte, II-től XII-ig számozva. A III. cikktől kezdve ezek Szőkefalvi-Nagy Béla közös munkái voltak fiatal román kollégájával, C. Foias-sal. Ezen dolgozatok képezték az alábbi híres könyv alapját, amelyben a szerzők az operátorelmélet egy fontos új ágát alkották meg.

B. Sz.-Nagy and C. Foias, Analyse harmonique des opérateurs de l'espace de Hilbert, Masson et Cie, Paris; Akadémiai Kiadó, Budapest 1967, xi+373 pp.

A könyvet lefordították orosz és angol nyelvre is. Az orosz fordítás M. G. Krein által írt előszavából idézünk (lásd [4]): „1953-ban a híres magyar matematikus B. Szőkefalvi-Nagy az Acta Scientiarum Mathematicarum (Szeged) folyóiratban publikált egy ma már széles körben ismert tételt kontrakciók unitér dilatációjáról. A munkát a szerző és más kutatók rögtön folytatták. 1958-ban a fiatal román matematikus C. Foias csatlakozott a kontrakciók elméletének kidolgozásához. B. Szőkefalvi-Nagy és C. Foias cikksorozatot publikáltak közös, »On the contractions of Hilbert Space« címen. A kutatás egy jól kidolgozott elméletet eredményezett, amely fontos szerepet játszik a modern funkcionálanalízisben.”

Most rátérünk T. Ando egy fontos dolgozatára, amely szorosan kapcsolódik Szőkefalvi-Nagy Béla fent említett dilatációs tételéhez.

T. Ando, On a pair of commutative contractions, Acta Sci. Math. (Szeged) 24 (1963), 88–90.

A MathSciNet szerinti 136 idézetével ez a legtöbbet idézett operátorelméleti dolgozat, amely a szegedi Acta-ban jelent meg. A Google Tudós 414 idézetet mutat rá. Ando ebben a cikkben bizonyította, hogy egy adott Hilbert-tér bármely kommutáló kontrakciópárjához van kommuntáló unitér hatványdilatációpár. A tétel egy Szőkefalvi-Nagy Béla által felvetett kérdést válaszol meg. Az érdekesség kedvéért említjük, hogy S. Parrott 1970-ben bebizonyította, hogy hasonló eredmény nem érvényes kommutáló kontrakció-hármasokra.

Végül a következő cikket említjük.

N. Dunford, Resolutions of the identity for commutative 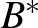-algebras of operators, Acta Sci. Math. (Szeged) 12 (1950), 51–56.

Ebben a munkában a szerző egy olyan bizonyítást adott a normális operátorok spektráltételére, amely a kommutatív 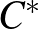$C^*$ -algebrák Gelfand–Naimark tételére, valamint a folytonos függvények terének korlátos lineáris funkcionáljaira vonatkozó Riesz-féle reprezentációs tétel Kakutani-féle általánosítására épült. Mára ez a megközelítés vált standarddá, a témával foglalkozó monográfiák és tankönyvek többsége ezt követi.

A fenti lista természetesen nem teljes, a megjelent nagyhatású cikkeket tovább lehetne sorolni.

3. A századik évforduló

A szegedi Acta 2022-ben ünnepelte alapításának 100. évfordulóját. Ez az első Magyarországon megjelent nemzetközi matematikai folyóirat, és a 20 legrégebbi, ma is aktív matematikai folyóirat egyike a világon. Az évforduló alkalmából több változtatást is végrehajtottunk a folyóirattal kapcsolatban. Mindenekelőtt kibővítettük a szerkesztőbizottságot. Az első 100 évben ez csak helyi tagokból állt, 2022-től több kiváló külföldi matematikus csatlakozott a testülethez. Emellett a lap kiadója is megváltozott. 2022-től a szegedi Acta a Springer Nature/Birkäuser kiadásában jelenik meg (a tulajdonos továbbra is a Szegedi Tudományegyetem Bolyai Intézete).

Az új borító

A folyóirat weboldala itt tekinthető meg, a szerkesztőbizottság tagjainak aktuális névsora pedig ide kattintva érhető el.

Fentebb már említettük, hogy Szőkefalvi-Nagy Béla főszerkesztősége idején a folyóirat fókuszában a funkcionálanalízis és az operátorelmélet állt. Ez motiválta egy kapcsolódó különszám megjelentetését (88. évfolyam 1-2. szám), amelyet a 100. évfordulónak szenteltünk. A funkcionálanalízis és operátorelmélet olyan neves kutatóit kértük fel aktuális munkáik benyújtására, akik korábban jelentős eredményeket publikáltak a szegedi Acta-ban. Számos értékes kéziratot kaptunk, és nemrég meg is jelent a meglehetősen vastag különszám.

A különszám mellett az emlékezetes esemény megünneplésére online konferenciát is szerveztünk. A 2022. május 5-6-án tartott rendezvényre több mint 200-an regisztráltak. Az elhangzott előadások felvétele a Springer Youtube csatornáján is elérhető.

4. Utószó

A folyóirat ilyen hosszú és fényes története után mit mondhatunk a jövőről? Nagyon röviden: igyekszünk továbbra is a nagy elődök nyomdokain járni, és ezzel párhuzamosan megfelelni a modern idők kihívásainak.

Bár a folyóirat fókuszterületei a funkcionálanalízis és az operátorelmélet, az eredeti hagyományt követve a szegedi Acta-t széles spektrumú matematikai folyóiratnak tekintjük. Nagyon szívesen fogadjuk az analízis egyéb területeiről, valamint az algebra és a geometria különböző területeiről érkező kiváló minőségű kéziratokat.

Az újjászervezett folyóirat friss lendülettel kezdi a következő időszakot, és mindent megteszünk annak érdekében, hogy a szegedi Acta hosszú távon tovább prosperáljon.

Irodalomjegyzék

: [1] R. Hersh and V. John-Steiner, A visit to Hungarian mathematics, Math. Intelligencer 15 (1993), 13–26. https://doi.org/10.1007/BF03024187

[2] E.R. Lorch, Szeged in 1934, Amer. Math. Monthly 100 (1993), 219–230. https://doi.org/10.1080/00029890.1993.11990392

[3] L. Rodríguez, Frigyes Riesz between the two world wars, BSHM Bull. 32 (2017), 235–245. https://doi.org/10.1080/17498430.2017.1326216

[4] B. Sz.-Nagy, C. Foias, H. Bercovici, L. Kérchy, Harmonic analysis of operators on Hilbert space. Second edition. Revised and enlarged edition. Universitext. Springer, New York, 2010. xiv+474 pp. ISBN: 978-1-4419-6093-1. https://doi.org/10.1007/978-1-4419-6094-8

[5] P. Weibel, Beyond Art: A Third Culture: a comparative study in cultures art and science in 20th century Austria and Hungary. Springer, 2005. https://doi.org/10.1007/3-211-37846-4

A fenti anyag eredetileg az EMS Magazine-ban jelent meg, https://euromathsoc.org/magazine/articles/113. A fordítást a European Mathematical Society jóváhagyta, annak elvégzésében Titkos Tamás nagy segítségére volt a szerzőnek.

Molnár Lajos egyetemi tanár
SZTE Bolyai Intézet