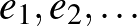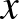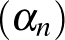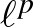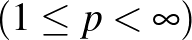1. Egy érdekes probléma és egy szokatlan díj
Stanislaw Mazur (1905–1981) lengyel matematikus 1936-ban az alábbi egyszerűnek megfogalmazható problémát tűzte ki:
|
Legyen ![$\displaystyle \left\vert f(x,y)-\sum_{i=1}^n \alpha_if(a_i,y)f(x,b_i)\right\vert<\varepsilon \qquad (\forall x,y\in[0,1])?
$](/images/stories/latexuj/2023-03/2023-03-skotkonyv/img6.png) |
A kérdés durván szólva az, hogy apprixomálható-e a függvény véges sok parciális függvényének segítségével. A kérdésre pozitív válasz adható, amennyiben 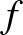 -ről még azt is feltesszük, hogy az valamelyik változójában folytonosan (parciálisan) differenciálható.
-ről még azt is feltesszük, hogy az valamelyik változójában folytonosan (parciálisan) differenciálható.
A differenciálhatósági feltététel nélkül azonban a probléma váratlanul nehéznek bizonyult, így a híres Skót Könyvben is helyet kapott, éspedig a 153-as számú problémaként:

Ahogy már egy korábbi Érintő cikkben is szerepelt, a híres lvivi Skót Kávéház olyan kiváló lengyel matematikusok gyülekező helye volt, mint Banach, Borsuk, Mazur, Kuratowski, Steinhaus, vagy épp Ulam. Egyes elmondások szerint Banach felesége, mások szerint maga Banach vásárolt egy kemény fedeles füzetet, amelybe a fontosabb matematikai problémákat feljegyezték. A füzet, amelynek első oldalán a Ksiega Szkocka, azaz Skót Könyv név szerepel, mindig a kávéházban volt elrejtve, a főpincértől lehetett elkérni, ha szükség volt rá.
Ami Mazur problémáját a többi kérdésnél emlékezetesebbé tette, az a megoldásért felkínált meglehetősen szokatlan díj: egy élő liba.
2. A bázis probléma
Habár Mazur 153-as számú próblémája egyszerűen megfogalmazható, meglehetősen bonyolultnak bizonyult, a megoldására egészen 1972-ig várni kellett. Alexander Grothendieck 1955-ös disszertációjában [4] megmutatta, hogy a kérdés egy hasonló természetű, de jóval mélyebb funkcionálanalízisbeli problémával, a kompakt operátorok approximálhatóságának problémájával ekvivalens.
Approximációs probléma: Igaz-e, hogy bármely Banach-terek között értelmezett kompakt operátor közelíthető-e véges rangú (azaz véges dimenziós képterű) operátorokkal? (Egy 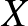 Banach-téren értelmezett Banach-téren értelmezett 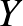 Banach-térbe képező lineáris leképezést kompaktnak nevezünk, ha az Banach-térbe képező lineáris leképezést kompaktnak nevezünk, ha az 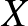 -beli egységgömb képe teljesen korlátos halmaz -beli egységgömb képe teljesen korlátos halmaz 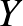 -ban.) Ha az -ban.) Ha az 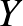 térre bármely térre bármely 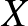 Banach-tér esetén igenlő a válasz, akkor azt mondjuk, hogy Banach-tér esetén igenlő a válasz, akkor azt mondjuk, hogy 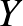 rendelkezik az approximációs tulajdonsággal. rendelkezik az approximációs tulajdonsággal. |
Grothendieck észrevétele alapján a 153-as probléma a funkcionálanalízis egy másik mély kérdésével, az ún. bázis problémával is összefüggésbe hozható. Ennek megfogalmázásához néhány fogalom ismertetése szükséges. Mint ismeretes, bármely vektortérben létezik algebrai bázis (vagy más néven Hamel-bázis), vagyis egy olyan vektor rendszer, amelynek segítségével minden vektor (véges) lineáris kombicióként előállítható. Banach-térben a lineáris kombinációk helyett végtelen sorösszeget is tekinthetünk, aminek segítségével a bázis fogalmának egy topológiai változatát értelmezhetjük.
|
Az 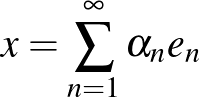 alakban valamely egyértelműen meghatározott 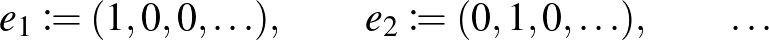 vektorok. Jóval kevésbé nyilvánvaló, de egy adott intervallum feletti folytonos függvények terében is megadható Schauder-bázis (ld. Faber-rendszer).
Juliusz Schauder (1899 – 1943) Bázis probléma: Igaz-e, hogy minden szeparábilis Banach-térnek létezik Schauder-bázisa? |
A bázis problémát Stefan Banach vetette fel 1932-es könyvében [1].
3. Per Enflo, a sokoldalú matematikus
1972-ben az akkor 28 éves Per Enflo svéd matematikus konstruált egy olyan szeparábilis Banach-teret, amely nem rendelkezik az approximációs tulajdonsággal, és emiatt egyúttal Schauder-bázis sem lehet benne. Ezzel az ellenpáldával Mazur 153-as számú kérdésére is negatív választ adott. Tehát az Acta Mathematica-ban publikált nyolc oldalas cikkével egyszerre három komoly problémát oldott meg. Az Amerikai Matematikai Társulat (AMS) 75 éves fennállásának apropóján Halmos Pál 1990-ben összegyűjtött néhány fontos témát illetve problémát [5], amelyben az utóbbi 75 évben komoly előrelépés történt. A bázis probléma megoldása és Per Enflo konstrukciója ott szerepel a fontos áttörések között.
Enflo a 153-as probléma megoldását még 1972-ben bemutatta Varsóban. Az előadáson Mazur is részt vett, és az 1936-ban tett ígéretét betartva egy élő libát is magával hozott. Egy lengyel újság egy fotót is közölt az emlékezetes díjátadóról.

Mazur átadja a megérdemelt díjat Enflonak
Érdemes megemlíteni, hogy a funkcionálanalízis egy másik nevezetes sejtésének, az úgynevezett invariáns altér problémának cáfolata is Enflo nevéhez fűződik.
Az invariáns altér probléma: Igaz-e, hogy bármely végtelen dimenziós 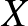 komplex Banach-téren értelmezett folytonos és lineáris komplex Banach-téren értelmezett folytonos és lineáris 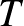 operátornak létezik operátornak létezik 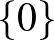 -tól és -tól és 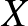 -től különböző zárt invariáns altere, vagyis olyan -től különböző zárt invariáns altere, vagyis olyan 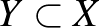 zárt altér, amelyet zárt altér, amelyet 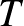 önmagába képez? önmagába képez? |
Enflo 1975-ben egy bonyolult ellenpéldával demonstrálta [3], hogy a sejtés nem igaz. Megjegyzendő, hogy az invariáns altér probléma Hilbert-terekben a mai napig nyitott.
 Enflo amellett, hogy zseniális matematikus, az élet több más területén is rendkívül tehetségnek bizonyult. Számos matematikai biológia témájú tanulmányt publikált, elsősorban a populációdinamika területén. Ezenkívül Enflo kiváló zongorista: 1956-ban valamint 1961-ben megnyerte a fiatal zongoristák versenyét Svédországban, 12 évesen pedig a Svéd Királyi Operazenekarban szólistaként játszott. Mesterei között megtalálhatjuk a világhírű magyar zongoraművészt, Anda Gézát is. Enflo számos szólófelvételt készített, és mind a mai napig rendszeresen koncertezik. Az alábbi felvétel a Lengyel Matematikai Társaság alapításának 100. évfordulóját ünneplő eseményen készült 2019-ben.
Enflo amellett, hogy zseniális matematikus, az élet több más területén is rendkívül tehetségnek bizonyult. Számos matematikai biológia témájú tanulmányt publikált, elsősorban a populációdinamika területén. Ezenkívül Enflo kiváló zongorista: 1956-ban valamint 1961-ben megnyerte a fiatal zongoristák versenyét Svédországban, 12 évesen pedig a Svéd Királyi Operazenekarban szólistaként játszott. Mesterei között megtalálhatjuk a világhírű magyar zongoraművészt, Anda Gézát is. Enflo számos szólófelvételt készített, és mind a mai napig rendszeresen koncertezik. Az alábbi felvétel a Lengyel Matematikai Társaság alapításának 100. évfordulóját ünneplő eseményen készült 2019-ben.
Irodalomjegyzék
- [1] S. Banach, Théorie des opérations linéaires, Warsawa, 1932.
- [2] P. Enflo, A counterexample to the approximation problem in Banach spaces, Acta Mathematica, (1973) 130:309–317.
- [3] P. Enflo, On the invariant subspace problem for Banach spaces, Acta Mathematica, (1987) 158:213–313.
- [4] A. Grothendieck, Produits tensoriels topologiques et espaces nucléaires, Memo. Amer. Math. Soc., 16 (1955).
- [5] P. R. Halmos, Has Progress in Mathematics Slowed Down?, Amer. Math. Monthly, Volume 97 (1990), 561–588.
- [6] R. D. Mauldin, The Scottish Book, Mathematics from The Scottish Café, with Selected Problems from The New Scottish Book, Springer International Publishing, Switzerland, 2015.
A cikk az NKFIH ÚNKP-22-5-ELTE-1096 kódszámú projektnek, valamint az MTA Bolyai János Kutatási Ösztöndíjának támogatásával készült.











![$[0,1]\times[0,1]$](/images/stories/latexuj/2023-03/2023-03-skotkonyv/img2.png)
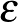
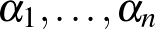
![$a_1,\ldots,a_n, b_1,\ldots,b_n\in [0,1]$](/images/stories/latexuj/2023-03/2023-03-skotkonyv/img5.png)